Серия Тейлора

По мере повышения степени полинома Тейлора он приближается к правильной функции. На этом изображении показаны sin x и его аппроксимации Тейлора полиномами степени 1 , 3 , 5 , 7 , 9 , 11 и 13 при x = 0 .

В математике или ряд Тейлора разложение Тейлора функции членов , представляет собой бесконечную сумму функции которые выражаются через производные в одной точке. Для большинства распространенных функций функция и сумма ее ряда Тейлора равны вблизи этой точки. Ряды Тейлора названы в честь Брука Тейлора , который представил их в 1715 году. Ряд Тейлора также называется рядом Маклорена , когда 0 — это точка, в которой рассматриваются производные, в честь Колина Маклорена , который широко использовал этот особый случай ряда Тейлора в 18 век.

Частичная сумма , образованная первыми n + 1 членами ряда Тейлора, представляет собой многочлен степени n , который называется n- м полиномом Тейлора функции. Полиномы Тейлора — это аппроксимации функции, которые обычно становятся более точными по мере увеличения n . Теорема Тейлора дает количественные оценки ошибки, вносимой использованием таких приближений. Если ряд Тейлора функции сходится , его сумма является пределом бесконечной последовательности полиномов Тейлора. Функция может отличаться от суммы своего ряда Тейлора, даже если ее ряд Тейлора сходится. Функция является аналитической в ​​точке x, если она равна сумме своего ряда Тейлора на некотором открытом интервале (или открытом круге в комплексной плоскости ), содержащем x . Это означает, что функция аналитична в каждой точке интервала (или круга).

Определение

Ряд Тейлора действительной или комплекснозначной функции f ( x ) , которая бесконечно дифференцируема по действительному или комплексному числу a , является степенным рядом

$$f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.$$

Вот, н ! обозначает факториал числа n . Функция f ^{( н )} ( a ) обозначает n- ю производную от f, вычисленную в точке a . Производная нулевого порядка f определяется как сама f и ( x − a ) ⁰ и 0! оба определены как 1 . Этот ряд можно записать, используя сигма-нотацию , как в правой формуле. При a = 0 ряд Маклорена принимает вид:

$$f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f'''(0)}{3!}}x^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}x^{n}.$$

Примеры

Ряд Тейлора любого многочлена является самим многочленом.

Серия Маклоренов. 1/1 − — x геометрическая прогрессия

$$1+x+x^{2}+x^{3}+\cdots .$$

Итак, заменив x на 1 − x , ряд Тейлора 1 / x при a = 1 равно

$$1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .$$

Интегрируя приведенный выше ряд Маклорена, мы находим ряд Маклорена для ln(1 − x ) , где ln обозначает натуральный логарифм :

$$-x-{\tfrac {1}{2}}x^{2}-{\tfrac {1}{3}}x^{3}-{\tfrac {1}{4}}x^{4}-\cdots .$$

Соответствующий ряд Тейлора для ln x при a = 1 равен

$$(x-1)-{\tfrac {1}{2}}(x-1)^{2}+{\tfrac {1}{3}}(x-1)^{3}-{\tfrac {1}{4}}(x-1)^{4}+\cdots ,$$

и, в более общем смысле, соответствующая серия Тейлора для ln x в произвольной ненулевой точке a равна:

$$\ln a+{\frac {1}{a}}(x-a)-{\frac {1}{a^{2}}}{\frac {\left(x-a\right)^{2}}{2}}+\cdots .$$

Ряд Маклорена показательной функции e ^Икс является

$${\begin{aligned}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}&={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots \\&=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots .\end{aligned}}$$

Приведенное выше разложение справедливо, поскольку производная e ^Икс по отношению к x также является e ^Икс , и е ⁰ равно 1. Остаются члены ( x − 0) ^н в числителе и n ! в знаменателе каждого члена бесконечной суммы.

История

Древнегреческий философ Зенон Элейский рассматривал проблему суммирования бесконечного ряда для достижения конечного результата, но отвергал ее как невозможную; результатом стал парадокс Зенона . Позже Аристотель предложил философское решение парадокса, но математическое содержание, по-видимому, оставалось неразрешенным, пока не было рассмотрено Архимедом , как это было до Аристотеля досократическим атомистом Демокритом . Архимеда Именно с помощью метода истощения можно было выполнить бесконечное количество последовательных подразделений для достижения конечного результата. Лю Хуэй независимо применил аналогичный метод несколько столетий спустя.

В 14 веке самые ранние примеры конкретных рядов Тейлора (но не общего метода) были приведены индийским математиком Мадхавой из Сангамаграмы . Хотя никаких записей о его работе не сохранилось, работы его последователей из школы астрономии и математики Кералы что он нашел ряд Тейлора для тригонометрических функций синуса предполагают , , косинуса и арктангенса (см. Ряд Мадхавы ). В течение следующих двух столетий его последователи разработали дальнейшие расширения рядов и рациональные аппроксимации.

В конце 1670 года Джеймсу Грегори было показано в письме Джона Коллинза несколько серий Маклорена ( ${\textstyle \sin x,}$ ${\textstyle \cos x,}$ ${\textstyle \arcsin x,}$ и ${\textstyle x\cot x}$), выведенный Исааком Ньютоном , и рассказал, что Ньютон разработал общий метод разложения функций в ряд. На самом деле Ньютон использовал громоздкий метод, включающий в себя длинное деление рядов и почленное интегрирование, но Грегори не знал об этом и решил открыть для себя общий метод. В начале 1671 года Грегори обнаружил что-то вроде общей серии Маклорена и отправил Коллинзу письмо, включающее серии для ${\textstyle \arctan x,}$ ${\textstyle \tan x,}$ ${\textstyle \sec x,}$ ${\textstyle \ln \,\sec x}$ (интеграл $\tan$), ${\textstyle \ln \,\tan {\tfrac {1}{2}}{{\bigl (}{\tfrac {1}{2}}\pi +x{\bigr )}}}$ ( интеграл от sec , обратная функция Гудермана ), ${\textstyle \operatorname {arcsec} {\bigl (}{\sqrt {2}}e^{x}{\bigr )},}$ и ${\textstyle 2\arctan e^{x}-{\tfrac {1}{2}}\pi }$(функция Гудермана). Однако, полагая, что он всего лишь переработал метод Ньютона, Грегори никогда не описывал, как он получил эти серии, и можно лишь предположить, что он понял общий метод, исследуя черновые записи, которые он нацарапал на обороте другого письма 1671 года.

В 1691–1692 годах Исаак Ньютон записал явное утверждение ряда Тейлора и Маклорена в неопубликованной версии своей работы De Quadratura Curvarum . Однако эта работа так и не была завершена, и соответствующие разделы были исключены из частей, опубликованных в 1704 году под названием Tractatus de Quadratura Curvarum .

Лишь в 1715 году общий метод построения этих рядов для всех функций, для которых они существуют, был наконец опубликован Бруком Тейлором , в честь которого теперь назван сериал.

Ряд Маклорена был назван в честь Колина Маклорена , профессора из Эдинбурга, опубликовавшего частный случай результата Тейлора в середине 18 века.

Аналитические функции

Основная статья: Аналитическая функция

Функция е ^{(−1/ х 2 )} не аналитична в точке x = 0 : ряд Тейлора тождественно равен 0, хотя функция таковой не является.

Если f ( x ) задается сходящимся степенным рядом в открытом диске с центром b на комплексной плоскости (или интервале действительной прямой), он называется аналитическим в этой области. Таким образом, для x в этой области f задается сходящимся степенным рядом

$$f(x)=\sum _{n=0}^{\infty }a_{n}(x-b)^{n}.$$

Дифференцируя по x приведенную выше формулу n раз, затем полагая x = b , получим:

$${\frac {f^{(n)}(b)}{n!}}=a_{n}$$

и поэтому разложение в степенной ряд согласуется с рядом Тейлора. Таким образом, функция является аналитической в ​​открытом диске с центром в точке b тогда и только тогда, когда ее ряд Тейлора сходится к значению функции в каждой точке диска.

Если f ( x ) равно сумме своего ряда Тейлора для всех x в комплексной плоскости, он называется целым . Полиномы, показательная функция e ^Икс и тригонометрические функции синус и косинус являются примерами целых функций. Примеры функций, которые не являются целыми, включают квадратный корень , логарифм , тангенс тригонометрической функции и ее обратную функцию, арктан . Для этих функций ряды Тейлора не сходятся , если x далек от b . То есть ряд Тейлора расходится в точке x , если расстояние между x и b больше радиуса сходимости . Ряд Тейлора можно использовать для вычисления значения целой функции в каждой точке, если значение функции и всех ее производных известны в одной точке.

Использование ряда Тейлора для аналитических функций включает:

1. Частичные суммы ( полиномы Тейлора ) ряда можно использовать в качестве аппроксимации функции. Эти приближения хороши, если в них включено достаточно много членов.
2. Дифференцирование и интегрирование степенных рядов можно выполнять почленно и, следовательно, это особенно легко.
3. Аналитическая функция однозначно продолжается до голоморфной функции на открытом диске в комплексной плоскости . Это делает доступным аппарат комплексного анализа .
4. (Усеченный) ряд можно использовать для численного вычисления значений функции (часто путем преобразования полинома в форму Чебышева и его оценки с помощью алгоритма Кленшоу ).
5. Алгебраические операции можно легко выполнить с представлением степенного ряда; например, формула Эйлера следует из разложения в ряд Тейлора тригонометрических и экспоненциальных функций. Этот результат имеет фундаментальное значение в такой области, как гармонический анализ .
6. Аппроксимации с использованием первых нескольких членов ряда Тейлора могут сделать возможными неразрешимые в противном случае проблемы для ограниченной области; этот подход часто используется в физике.

аппроксимации

Основная статья: теорема Тейлора

Синусоидальная функция (синяя) точно аппроксимируется полиномом Тейлора 7-й степени (розовый) для полного периода с центром в начале координат.

Полиномы Тейлора для ln(1 + x ) обеспечивают точные аппроксимации только в диапазоне −1 < x ≤ 1 . Для x > 1 полиномы Тейлора более высокой степени обеспечивают худшие приближения.

Приближения Тейлора для ln(1 + x ) (черный). При x > 1 аппроксимации расходятся.

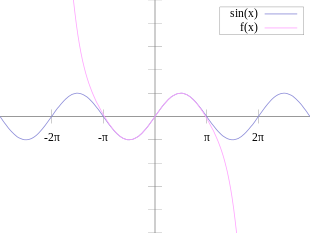
На рисунке изображена точная аппроксимация sin x вокруг точки x = 0 . Розовая кривая представляет собой полином седьмой степени:

$$\sin {x}\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}.\!$$

Погрешность этого приближения не более | х | ⁹ / 9! . Для полного цикла с центром в начале координат ( −π < x < π ) ошибка составляет менее 0,08215. В частности, для −1 < x < 1 ошибка меньше 0,000003.

Напротив, также показано изображение функции натурального логарифма ln(1 + x ) и некоторых ее полиномов Тейлора вокруг a = 0 . Эти приближения сходятся к функции только в области −1 < x ≤ 1 ; за пределами этой области полиномы Тейлора более высокой степени являются худшим приближением для функции.

Ошибка , возникающая при приближении функции ее полиномом Тейлора n -й степени, называется остатком или невязкой и обозначается функцией R _n ( x ) . Теорему Тейлора можно использовать для получения оценки размера остатка .

В общем случае ряд Тейлора не обязательно должен быть сходящимся вообще . И на самом деле множество функций со сходящимся рядом Тейлора представляет собой скудное множество в пространстве Фреше гладких функций . И даже если ряд Тейлора функции f сходится, ее предел вообще не обязательно должен быть равен значению функции f ( x ) . Например, функция

$$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if }}x=0\end{cases}}$$

в бесконечно дифференцируема точке x = 0 и имеет там все производные равны нулю. Следовательно, ряд Тейлора функции f ( x ) относительно x = 0 тождественно равен нулю. Однако f ( x ) не является нулевой функцией, поэтому не равна ряду Тейлора вокруг начала координат. Таким образом, f ( x ) является примером неаналитической гладкой функции .

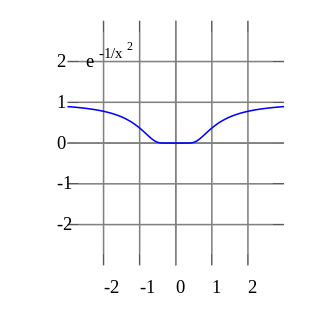
В реальном анализе этот пример показывает, что существуют бесконечно дифференцируемые функции f ( x ) , ряды Тейлора которых не равны f ( x ) , даже если они сходятся. Напротив, голоморфные функции , изучаемые в комплексном анализе, всегда обладают сходящимся рядом Тейлора, и даже ряд Тейлора мероморфных функций , которые могут иметь особенности, никогда не сходятся к значению, отличному от самой функции. Комплексная функция e ^{−1/ z 2} , однако не приближается к 0, когда z приближается к 0 вдоль мнимой оси, поэтому он не является непрерывным в комплексной плоскости, а его ряд Тейлора не определен в точке 0.

В более общем смысле, каждая последовательность действительных или комплексных чисел может появиться как коэффициенты в ряду Тейлора бесконечно дифференцируемой функции, определенной на действительной прямой, что является следствием леммы Бореля . В результате радиус сходимости ряда Тейлора может быть равен нулю. Существуют даже бесконечно дифференцируемые функции, определенные на вещественной прямой, ряды Тейлора которых всюду имеют радиус сходимости 0.

Функцию нельзя записать в виде ряда Тейлора с центром в особенности ; в этих случаях часто все же можно добиться разложения в ряд, если допустить также отрицательные степени переменной x ; см . серию Лорана . Например, f ( x ) = e ^{−1/ х 2} можно записать в виде ряда Лорана.

Обобщение

Обобщение ряда Тейлора сходится к значению самой функции для любой ограниченной непрерывной функции на (0,∞) , и это можно сделать с помощью исчисления конечных разностей . В частности, следующая теорема Эйнара Хилле о том, что для любого t > 0

$$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h}^{n}f(a)}{h^{n}}}=f(a+t).$$

Здесь ∆ ^н
_h — n-й конечно-разностный оператор с размером шага h . Ряд представляет собой в точности ряд Тейлора, с той лишь разницей, что вместо дифференцирования появляются разделенные разности: формально ряд подобен ряду Ньютона . Когда функция f аналитична в точке a , члены ряда сходятся к членам ряда Тейлора и в этом смысле обобщают обычный ряд Тейлора.

В общем, для любой бесконечной последовательности a _i справедливо следующее тождество степенного ряда:

$$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j=0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$$

Так, в частности,

$$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$$

Ряд справа — это ожидаемое значение f ( a + X ) , где X — , распределенная по Пуассону случайная величина , принимающая значение jh с вероятностью e. ^{− т / ч} · ( т / ч ) ^дж / дж ! . Следовательно,

$$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h}(x).$$

Закон больших чисел подразумевает, что тождество справедливо.

серии Маклорена некоторых

См. Также: Список математических рядов.

Далее следует несколько важных расширений серии Маклорена. Все эти расширения действительны для комплексных аргументов x .

Экспоненциальная функция

Показательная функция e ^Икс (синим цветом) и сумму первых n + 1 членов его ряда Тейлора в точке 0 (красным цветом).

Показательная функция $e^{x}$ (с основанием e ) имеет ряд Маклорена

$$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots .$$

Оно сходится для всех x .

Экспоненциальная производящая функция чисел Белла является показательной функцией предшественника показательной функции:

$$\exp(\exp {x}-1)=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}$$

Натуральный логарифм

Натуральный логарифм (с основанием e ) имеет ряд Маклорена.

$${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots ,\\\ln(1+x)&=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots .\end{aligned}}$$

Последняя серия известна как серия Меркатора , названная в честь Николая Меркатора (так как она была опубликована в его трактате 1668 года «Логарифмотехния »). Оба эти ряда сходятся при $|x|<1$. (Кроме того, ряд для ln(1 − x ) сходится при x = −1 , а ряд для ln(1 + x ) сходится при x = 1. )

Геометрическая серия

Геометрическая прогрессия и ее производные имеют ряд Маклорена.

$${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{(1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3}}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{aligned}}$$

Все сходятся для $|x|<1$. Это частные случаи биномиального ряда, приведенные в следующем разделе.

Биномиальный ряд

Биномиальный ряд – это степенной ряд

$$(1+x)^{\alpha }=\sum _{n=0}^{\infty }{\binom {\alpha }{n}}x^{n}$$

чьи коэффициенты являются обобщенными биномиальными коэффициентами

$${\binom {\alpha }{n}}=\prod _{k=1}^{n}{\frac {\alpha -k+1}{k}}={\frac {\alpha (\alpha -1)\cdots (\alpha -n+1)}{n!}}.$$

(Если n = 0 , это произведение является пустым произведением и имеет значение 1.) Оно сходится при $|x|<1$ для любого действительного или комплексного числа α .

Когда α = −1 , это, по сути, бесконечная геометрическая серия, упомянутая в предыдущем разделе. Особые случаи α = 1/2 ​ и = α − 1/2 дают обратную функцию квадратного корня и ей :

$${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+{\frac {7}{256}}x^{5}-\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n!)^{2}(2n-1)}}x^{n},\\(1+x)^{-{\frac {1}{2}}}&=1-{\frac {1}{2}}x+{\frac {3}{8}}x^{2}-{\frac {5}{16}}x^{3}+{\frac {35}{128}}x^{4}-{\frac {63}{256}}x^{5}+\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}}}x^{n}.\end{aligned}}$$

только линейный член Когда сохраняется , это упрощается до биномиальной аппроксимации .

Тригонометрические функции

Обычные тригонометрические функции и их обратные имеют следующий ряд Маклорена:

$${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{for all }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{for all }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{aligned}}$$

Все углы выражаются в радианах . Числа Bk _, входящие в разложение tan x , являются числами Бернулли . E k _{являются} в разложении sec x числами Эйлера .

Гиперболические функции

Гиперболические функции имеют ряды Маклорена, тесно связанные с рядами для соответствующих тригонометрических функций:

$${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{for all }}x\\[6pt]\cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots &&{\text{for all }}x\\[6pt]\tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm 1\end{aligned}}$$

Числа Bk _, входящие в ряд для tanh x , являются числами Бернулли .

Полилогарифмические функции

Полилогарифмы имеют следующие определяющие тождества:

$${\begin{aligned}{\text{Li}}_{2}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}x^{n}\\{\text{Li}}_{3}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}x^{n}\end{aligned}}$$

определяются Функции хи Лежандра следующим образом:

$${\begin{aligned}\chi _{2}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{2}}}x^{2n+1}\\\chi _{3}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}$$

А формулы, представленные ниже, называются обратными касательными интегралами :

$${\begin{aligned}{\text{Ti}}_{2}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{2}}}x^{2n+1}\\{\text{Ti}}_{3}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}$$

В статистической термодинамике эти формулы имеют большое значение.

Эллиптические функции

Полные эллиптические интегралы первого рода K и второго рода E можно определить следующим образом:

$${\begin{aligned}{\frac {2}{\pi }}K(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}\\{\frac {2}{\pi }}E(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}\end{aligned}}$$

описывают Тета-функции Якоби мир эллиптических модулярных функций и имеют следующие ряды Тейлора:

$${\begin{aligned}\vartheta _{00}(x)&=1+2\sum _{n=1}^{\infty }x^{n^{2}}\\\vartheta _{01}(x)&=1+2\sum _{n=1}^{\infty }(-1)^{n}x^{n^{2}}\end{aligned}}$$

Обычная последовательность номеров разделов P(n) имеет следующую производящую функцию:

$$\vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{-2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}=\sum _{n=0}^{\infty }P(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{k}}}$$

Строгая последовательность номеров разделов Q(n) имеет такую ​​производящую функцию:

$$\vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{-1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}=\sum _{n=0}^{\infty }Q(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}$$

Вычисление ряда Тейлора

Существует несколько методов вычисления рядов Тейлора для большого числа функций. Можно попытаться использовать определение ряда Тейлора, хотя это часто требует обобщения вида коэффициентов по легко кажущейся схеме. В качестве альтернативы можно использовать такие манипуляции, как замена, умножение или деление, сложение или вычитание стандартного ряда Тейлора, чтобы построить ряд Тейлора функции, поскольку ряд Тейлора является степенным рядом. В некоторых случаях можно также вывести ряд Тейлора, многократно применяя интегрирование по частям . Особенно удобно использование систем компьютерной алгебры для вычисления рядов Тейлора.

Первый пример

Чтобы вычислить полином Маклорена 7-й степени для функции

$$f(x)=\ln(\cos x),\quad x\in {\bigl (}{-{\tfrac {\pi }{2}}},{\tfrac {\pi }{2}}{\bigr )},$$

можно сначала переписать функцию как

$$f(x)={\ln }{\bigl (}1+(\cos x-1){\bigr )},$$

композиция двух функций $x\mapsto \ln(1+x)$ и $x\mapsto \cos x-1.$ Ряд Тейлора для натурального логарифма равен (с использованием обозначения «большое О» )

$$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+O{\left(x^{4}\right)}$$

и для функции косинуса

$$\cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+O{\left(x^{8}\right)}.$$

Первые несколько членов второго ряда можно подставить в каждый член первого ряда. Поскольку первый член второго ряда имеет степень 2, трех членов первого ряда достаточно, чтобы получить полином 7-й степени:

$${\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+O{\left((\cos x-1)^{4}\right)}\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {x^{6}}{45}}+O{\left(x^{8}\right)}.\end{aligned}}\!$$

Поскольку косинус — четная функция , коэффициенты при всех нечетных степенях равны нулю.

Второй пример

Предположим, нам нужен ряд Тейлора в нуле функции

$$g(x)={\frac {e^{x}}{\cos x}}.\!$$

Ряд Тейлора для показательной функции равен

$$e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots ,$$

и ряд для косинуса

$$\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots .$$

Предположим, что ряд для их частного равен

$${\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots$$

Умножение обеих частей на знаменатель $\cos x$ а затем разложив его в ряд, получим

$${\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\[5mu]&=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\left(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}}+{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \end{aligned}}$$

Сравнивая коэффициенты $g(x)\cos x$ с коэффициентами $e^{x},$

$$c_{0}=1,\ \ c_{1}=1,\ \ c_{2}-{\tfrac {1}{2}}c_{0}={\tfrac {1}{2}},\ \ c_{3}-{\tfrac {1}{2}}c_{1}={\tfrac {1}{6}},\ \ c_{4}-{\tfrac {1}{2}}c_{2}+{\tfrac {1}{24}}c_{0}={\tfrac {1}{24}},\ \ldots .$$

Коэффициенты $c_{i}$ из серии для $g(x)$ таким образом, можно вычислять по одному, что равносильно длинному делению ряда для $e^{x}$ и $\cos x$:

$${\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\tfrac {2}{3}}x^{3}+{\tfrac {1}{2}}x^{4}+\cdots .$$

Третий пример

Здесь мы используем метод, называемый «косвенным расширением», для расширения данной функции. Этот метод использует известное разложение Тейлора показательной функции. Чтобы разложить (1 + x ) e ^Икс в качестве ряда Тейлора по x мы используем известный ряд Тейлора функции e ^Икс :

$$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots .$$

Таким образом,

$${\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!}}+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end{aligned}}$$

Ряд

Классически алгебраические функции определяются алгебраическим уравнением, а трансцендентные функции (включая обсуждавшиеся выше) определяются некоторым свойством, которое для них выполняется, например дифференциальным уравнением . Например, показательная функция — это функция, которая всюду равна своей производной и принимает значение 1 в начале координат. Однако с таким же успехом можно определить аналитическую функцию через ее ряд Тейлора.

Ряды Тейлора используются для определения функций и « операторов » в различных областях математики. В частности, это верно в тех областях, где классические определения функций не работают. Например, используя ряды Тейлора, можно расширить аналитические функции до наборов матриц и операторов, таких как матричная экспонента или матричный логарифм .

В других областях, например формальном анализе, удобнее работать непосредственно с самими степенными рядами . Таким образом, можно определить решение дифференциального уравнения как степенной ряд, который, как мы надеемся доказать, является рядом Тейлора искомого решения.

Ряд Тейлора от нескольких переменных

Ряд Тейлора также можно обобщить на функции более чем одной переменной с

$${\begin{aligned}T(x_{1},\ldots ,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots ,a_{d})\\&=f(a_{1},\ldots ,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots ,a_{d})}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots ,a_{d})}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\cdots \end{aligned}}$$

Например, для функции $f(x,y)$ который зависит от двух переменных, x и y , ряд Тейлора второго порядка относительно точки ( a , b ) равен

$$f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){\Big )}$$

где нижние индексы обозначают соответствующие частные производные .

Ряд Тейлора второго порядка

См. Также: Линеаризация § Функции с несколькими переменными.

Разложение скалярной функции более чем одной переменной в ряд Тейлора второго порядка можно компактно записать как

$$T(\mathbf {x} )=f(\mathbf {a} )+(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}Df(\mathbf {a} )+{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a} )\right\}(\mathbf {x} -\mathbf {a} )+\cdots ,$$

где D f ( a ) — градиент f , оцененный при x = a и D ² f ( a ) — матрица Гессе . Применяя многоиндексное обозначение, ряд Тейлора для нескольких переменных становится

$$T(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a} )^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\mathbf {a} ),$$

которое следует понимать как еще более сокращенную многоиндексную версию первого уравнения этого параграфа с полной аналогией случаю с одной переменной.

Пример

Аппроксимация ряда Тейлора второго порядка (оранжевым цветом) функции f ( x , y ) = e ^Икс ln(1 + y ) вокруг начала координат.

Чтобы вычислить разложение в ряд Тейлора второго порядка вокруг точки ( a , b ) = (0, 0) функции

$$f(x,y)=e^{x}\ln(1+y),$$

сначала вычисляются все необходимые частные производные:

$${\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1+y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{(1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{aligned}}$$

Оценка этих производных в начале координат дает коэффициенты Тейлора.

$${\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\\f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{aligned}}$$

Подставив эти значения в общую формулу

$${\begin{aligned}T(x,y)=&f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)\\&{}+{\frac {1}{2!}}\left((x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b)\right)+\cdots \end{aligned}}$$

производит

$${\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\big )}+\cdots \\&=y+xy-{\tfrac {1}{2}}y^{2}+\cdots \end{aligned}}$$

Поскольку ln(1 + y ) аналитична в | й | < 1 , мы имеем

$$e^{x}\ln(1+y)=y+xy-{\tfrac {1}{2}}y^{2}+\cdots ,\qquad |y|<1.$$

с

Основная статья: ряд Фурье

Тригонометрический ряд Фурье позволяет выразить периодическую функцию (или функцию, определенную на замкнутом интервале [ a , b ] ) как бесконечную сумму тригонометрических функций ( синусов и косинусов ). В этом смысле ряд Фурье аналогичен ряду Тейлора, поскольку последний позволяет выразить функцию в виде бесконечной суммы степеней . Тем не менее, эти две серии отличаются друг от друга по нескольким важным вопросам:

• Все конечные усечения ряда Тейлора функции f ( x ) относительно точки x = a в точности равны f в точке a . Напротив, ряд Фурье вычисляется путем интегрирования по всему интервалу, поэтому обычно не существует такой точки, в которой все конечные усечения ряда были бы точными.
• Вычисление ряда Тейлора требует знания функции в произвольной малой окрестности точки, тогда как вычисление ряда Фурье требует знания функции во всем ее интервале определения . В определенном смысле можно сказать, что ряд Тейлора является «локальным», а ряд Фурье — «глобальным».
• Ряд Тейлора определяется для функции, которая имеет бесконечное число производных в одной точке, тогда как ряд Фурье определяется для любой интегрируемой функции . В частности, функция не может быть нигде дифференцируемой. (Например, f ( x ) может быть функцией Вейерштрасса .)
• Сходимость обоих рядов имеет весьма разные свойства. Даже если ряд Тейлора имеет положительный радиус сходимости, полученный ряд может не совпадать с функцией; но если функция аналитическая, то ряд сходится поточечно к функции и равномерно на каждом компактном подмножестве интервала сходимости. Что касается ряда Фурье, то если функция интегрируема с квадратом, то этот ряд сходится в среднем квадратичном , но необходимы дополнительные требования для обеспечения поточечной или равномерной сходимости (например, если функция периодическая и принадлежит классу C ¹ тогда сходимость равномерная).
• Наконец, на практике нужно аппроксимировать функцию конечным числом членов, скажем, полиномом Тейлора или частичной суммой тригонометрического ряда соответственно. В случае ряда Тейлора ошибка очень мала в окрестности точки, где она вычисляется, но может быть очень большой в удаленной точке. В случае ряда Фурье ошибка распределяется по области определения функции.

См. также

• Асимптотическое расширение
• Генерирующая функция
• Лоран серии
• Серия Мадхава
• Интерполяция разделенной разности Ньютона
• Аппроксимант Паде
• Серия Пюизо
• Оператор смены

Ссылки

• Абрамовиц, Милтон ; Стегун, Ирен А. (1970). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Нью-Йорк: Dover Publications . Девятое издание.
• Баннер, Адриан (2007). Спасатель исчисления: все инструменты, необходимые для достижения успеха в исчислении . Издательство Принстонского университета. ISBN  978-0-691-13088-0 .
• Билодо, Джеральд; Тай, Пол; Кио, GE (2010). Введение в анализ . Издательство Джонс и Бартлетт. ISBN  978-0-7637-7492-9 .
• Бойер, К.; Мерцбах, У. (1991). История математики (2-е изд.). Джон Уайли и сыновья. ISBN  0-471-09763-2 .
• Брюс, Ян (2007). «Метод прямых и обратных приращений]» . 17 Centurymaths.com .
• Дэни, С.Г. (2012). «Древнеиндийская математика – Конспект». Резонанс . 17 (3): 236–246. дои : 10.1007/s12045-012-0022-y . S2CID   120553186 .
• Фейгенбаум, Л. (1985). «Брук Тейлор и метод приращений». Архив истории точных наук . 34 (1–2): 1–140. дои : 10.1007/bf00329903 . S2CID   122105736 .
• Феллер, Уильям (2003) [1971]. Введение в теорию вероятностей и ее приложения . Том. 2 (3-е изд.). Уайли. ISBN  9789971512989 . OCLC   818811840 .
• Гринберг, Майкл (1998). Высшая инженерная математика (2-е изд.). Прентис Холл. ISBN  0-13-321431-1 .
• Хилле, Эйнар ; Филлипс, Ральф С. (1957). Функциональный анализ и полугруппы . Публикации коллоквиума AMS. Том. 31. Американское математическое общество.
• Хофманн, Йозеф Эренфрид (1939). «Об открытии логарифмического ряда и его развитии в Англии до Кота». Национальный математический журнал . 14 (1): 33–45. дои : 10.2307/3028095 . JSTOR   3028095 .
• Хёрмандер, Ларс (2002) [1990]. «1. Тестовые функции §1.1. Обзор дифференциального исчисления» . Анализ операторов в частных производных . Том. 1 (2-е изд.). Спрингер. дои : 10.1007/978-3-642-61497-2_2 . ISBN  978-3-642-61497-2 .
• Клайн, М. (1990). Математическая мысль от древности до современности . Нью-Йорк: Издательство Оксфордского университета. ISBN  0-19-506135-7 .
• Колк, Йохан AC; Дуйстермаат, Джей Джей (2010). «Разложение Тейлора по нескольким переменным» . Распределения: Теория и приложения . Биркгаузер. дои : 10.1007/978-0-8176-4675-2_6 . ISBN  978-0-8176-4672-1 .
• Линдберг, Дэвид (2007). Начало западной науки (2-е изд.). Издательство Чикагского университета. ISBN  978-0-226-48205-7 .
• Малет, Антони (1993). «Джеймс Грегори о касательных и правиле Тейлора для разложения рядов». Архив истории точных наук . 46 (2): 97–137. дои : 10.1007/BF00375656 . JSTOR   41133959 . S2CID   120101519 .
• Рой, Ранджан (1990). «Открытие формулы ряда для числа π Лейбницем, Грегори и Нилакантой » (PDF) . Журнал «Математика» . 63 (5): 291–306. дои : 10.1080/0025570X.1990.11977541 .
• —— (2021) [2011]. Серии и произведения в развитии математики . Том. 1 (2-е изд.). Издательство Кембриджского университета.
• Рудин, Уолтер (1980). Реальный и комплексный анализ . Нью-Дели: МакГроу-Хилл. ISBN  0-07-099557-5 .
• Струйк, диджей (1969). Справочник по математике 1200–1800 гг . Издательство Гарвардского университета. ISBN  978-0-674-82355-6 .
• Тейлор, Брук (1715). методы приращения ( Прямой и обратный на латыни). Лондон.
• Томас, Джордж Б. младший; Финни, Росс Л. (1996). Исчисление и аналитическая геометрия (9-е изд.). Эддисон Уэсли. ISBN  0-201-53174-7 .
• Тернбулл, Герберт Вестрен, изд. (1939). Джеймс Грегори; Том памяти трехсотлетия . Дж. Белл и сыновья.

Внешние ссылки

• «Ряд Тейлора» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Серия Тейлора» . Математический мир .