Полилогарифм

Не путать с полилогарифмической функцией или логарифмической интегральной функцией .

В математике полилогарифм специальная (также известный как функция Жонкьера , по имени Альфреда Жонкьера) — это функция Li _s ( z ) порядка s и аргумента z . Только для особых значений s полилогарифм сводится к элементарной функции, такой как натуральный логарифм или рациональная функция . В квантовой статистике функция полилогарифма появляется как замкнутая форма интегралов распределения Ферми -Дирака и распределения Бозе-Эйнштейна , а также известна как интеграл Ферми-Дирака или интеграл Бозе-Эйнштейна . В квантовой электродинамике положительного полилогарифмы целого порядка возникают при расчете процессов, представленных диаграммами Фейнмана высшего порядка .

Функция полилогарифма эквивалентна дзета-функции Гурвица — любая функция может быть выражена через другую — и обе функции являются частными случаями трансцендента Лерха . Полилогарифмы не следует путать ни с полилогарифмическими функциями , ни со смещенным логарифмическим интегралом Li( z ) , который имеет такое же обозначение без нижнего индекса.

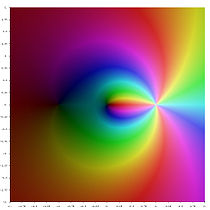
• Различные функции полилогарифма в комплексной плоскости
• 
  Ли _–3 ( z )
• 
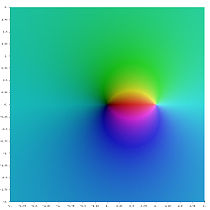
  Ли _–2 ( z )
• 
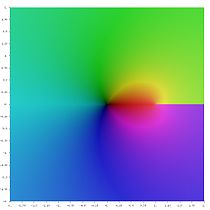
  Ли _–1 ( z )
• 
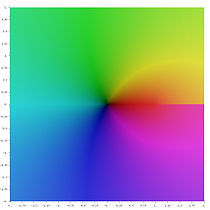
  Ли ₀ ( z )
• 
  Ли ₁ ( z )
• 
  Ли ₂ ( z )
• 
  Ли ₃ ( z )

Функция полилогарифма определяется степенным рядом по z , который также является рядом Дирихле по s :

$$\operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}=z+{z^{2} \over 2^{s}}+{z^{3} \over 3^{s}}+\cdots$$

Это определение справедливо для произвольного комплексного порядка s и для всех комплексных аргументов z с | г | < 1 ; его можно расширить до | г | ≥ 1 методом аналитического продолжения . (Здесь знаменатель k ^с понимается как exp( s ln k ) ). Особый случай s = 1 включает в себя обычный натуральный логарифм Li 1 ₍ z ) = −ln(1− z ) , а особые случаи s = 2 и s = 3 называются дилогарифмом (также называемым функцией Спенса) и трилогарифм соответственно. Название функции связано с тем, что ее также можно определить как повторяющийся интеграл самой себя:

$$\operatorname {Li} _{s+1}(z)=\int _{0}^{z}{\frac {\operatorname {Li} _{s}(t)}{t}}dt$$

таким образом, дилогарифм является интегралом функции, включающей логарифм, и так далее. Для неположительных целых порядков s полилогарифм является рациональной функцией .

Свойства

В случае, когда приказ $s$ является целым числом, оно будет представлено $s=n$ (или $s=-n$ когда отрицательный). Часто бывает удобно определить $\mu =\ln(z)$ где $\ln(z)$ является главной ветвью комплексного логарифма $\operatorname {Ln} (z)$ так что $-\pi <\operatorname {Im} (\mu )\leq \pi .$ Кроме того, все возведения в степень будут считаться однозначными: $z^{s}=\exp(s\ln(z)).$

В зависимости от заказа $s$, полилогарифм может быть многозначным. Главный филиал г. $\operatorname {Li} _{s}(z)$ принято отдавать за $|z|<1$ согласно приведенному выше определению ряда и считается непрерывным, за исключением положительной действительной оси, где разрез производится из $z=1$ к $\infty$ так, чтобы ось располагалась в нижней полуплоскости $z$. С точки зрения $\mu$, это составляет $-\pi <\arg(-\mu )\leq \pi$. Разрыв полилогарифма в зависимости от $\mu$ иногда может сбивать с толку.

Для реального спора $z$, полилогарифм вещественного порядка $s$ реально, если $z<1$, и его мнимая часть для $z\geq 1$ ( Вуд 1992 , §3):

$$\operatorname {Im} \left(\operatorname {Li} _{s}(z)\right)=-{{\pi \mu ^{s-1}} \over {\Gamma (s)}}.$$

Переходя к разрезу, если ε — бесконечно малое положительное действительное число, то:

$$\operatorname {Im} \left(\operatorname {Li} _{s}(z+i\epsilon )\right)={{\pi \mu ^{s-1}} \over {\Gamma (s)}}.$$

Оба вывода можно сделать из разложения в ряд ( см. ниже ) Li _s ( e ^м ) около µ = 0.

Производные полилогарифма следуют из определяющего степенного ряда:

$$z{\frac {\partial \operatorname {Li} _{s}(z)}{\partial z}}=\operatorname {Li} _{s-1}(z)$$

$${\frac {\partial \operatorname {Li} _{s}(e^{\mu })}{\partial \mu }}=\operatorname {Li} _{s-1}(e^{\mu }).$$

Квадратное соотношение видно из определения ряда и связано с формулой дублирования (см. также Клюни (1954) , Шредингер (1952) ):

$$\operatorname {Li} _{s}(-z)+\operatorname {Li} _{s}(z)=2^{1-s}\operatorname {Li} _{s}(z^{2}).$$

Функция Куммера подчиняется очень похожей формуле дублирования. Это частный случай формулы умножения для любого положительного целого числа p :

$$\sum _{m=0}^{p-1}\operatorname {Li} _{s}(ze^{2\pi im/p})=p^{1-s}\operatorname {Li} _{s}(z^{p}),$$

что можно доказать с помощью определения полилогарифма в виде ряда и ортогональности экспоненциальных членов (см., например, дискретное преобразование Фурье ).

Другое важное свойство, формула обращения, включает в себя дзета-функцию Гурвица или полиномы Бернулли и находится в связи с другими функциями ниже.

Особые ценности

В частных случаях полилогарифм может быть выражен через другие функции ( см. ниже ). Таким образом, конкретные значения полилогарифма можно также найти как частные значения этих других функций.

1. Для целых значений порядка полилогарифма повторным применением z ·∂/∂ z к Li ₁ ( z ) получаются следующие явные выражения:
   $$\operatorname {Li} _{1}(z)=-\ln(1-z)$$
   $$\operatorname {Li} _{0}(z)={z \over 1-z}$$
   $$\operatorname {Li} _{-1}(z)={z \over (1-z)^{2}}$$
   $$\operatorname {Li} _{-2}(z)={z(1+z) \over (1-z)^{3}}$$
   $$\operatorname {Li} _{-3}(z)={z(1+4z+z^{2}) \over (1-z)^{4}}$$
   $$\operatorname {Li} _{-4}(z)={z(1+z)(1+10z+z^{2}) \over (1-z)^{5}}.$$
   Соответственно, полилогарифм сводится к отношению полиномов от z и, следовательно, является рациональной функцией от z для всех неположительных целых порядков. Общий случай может быть выражен в виде конечной суммы:
   $$\operatorname {Li} _{-n}(z)=\left(z{\partial \over \partial z}\right)^{n}{z \over {1-z}}=\sum _{k=0}^{n}k!S(n+1,k+1)\left({z \over {1-z}}\right)^{k+1}\qquad (n=0,1,2,\ldots ),$$
   где S ( n , k ) — числа Стирлинга второго рода . Эквивалентные формулы, применимые к отрицательным целым порядкам: ( Wood 1992 , § 6):
   $$\operatorname {Li} _{-n}(z)=(-1)^{n+1}\sum _{k=0}^{n}k!S(n+1,k+1)\left({{-1} \over {1-z}}\right)^{k+1}\qquad (n=1,2,3,\ldots ),$$
   и:
   $$\operatorname {Li} _{-n}(z)={1 \over (1-z)^{n+1}}\sum _{k=0}^{n-1}\left\langle {n \atop k}\right\rangle z^{n-k}\qquad (n=1,2,3,\ldots ),$$
   где $\scriptstyle \left\langle {n \atop k}\right\rangle$ являются числами Эйлера . Все корни Li _{− n} ( z ) различны и вещественны; они включают z = 0, а остаток отрицательный и сосредоточен около z = -1 в логарифмическом масштабе. По мере того, как n становится большим, численная оценка этих рациональных выражений все больше страдает от отмены ( Wood 1992 , § 6); однако полную точность можно получить, вычислив Li _{− n} ( z ) через общее соотношение с дзета-функцией Гурвица ( см. ниже ).
2. Некоторые конкретные выражения для полуцелых значений аргумента z :
   $$\operatorname {Li} _{1}({\tfrac {1}{2}})=\ln 2$$
   $$\operatorname {Li} _{2}({\tfrac {1}{2}})={\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2}}(\ln 2)^{2}$$
   $$\operatorname {Li} _{3}({\tfrac {1}{2}})={\tfrac {1}{6}}(\ln 2)^{3}-{\tfrac {1}{12}}\pi ^{2}\ln 2+{\tfrac {7}{8}}\zeta (3),$$
   где ζ – дзета-функция Римана . Никакие формулы этого типа для более высоких целых порядков не известны ( Lewin 1991 , стр. 2), но есть, например ( Borwein, Borwein & Girgensohn 1995 ):
   $$\operatorname {Li} _{4}({\tfrac {1}{2}})={\tfrac {1}{360}}\pi ^{4}-{\tfrac {1}{24}}(\ln 2)^{4}+{\tfrac {1}{24}}\pi ^{2}(\ln 2)^{2}-{\tfrac {1}{2}}\zeta ({\bar {3}},{\bar {1}}),$$
   который включает в себя попеременную двойную сумму
   $$\zeta ({\bar {3}},{\bar {1}})=\sum _{m>n>0}(-1)^{m+n}m^{-3}n^{-1}.$$
   В общем случае для целых порядков n ≥ 2 ( Broadhurst 1996 , стр. 9):
   $$\operatorname {Li} _{n}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},\left\{1\right\}^{n-2}),$$
   где ζ ( s1 _sk ,..., ) _– кратная дзета-функция ; например:
   $$\operatorname {Li} _{5}({\tfrac {1}{2}})=-\zeta ({\bar {1}},{\bar {1}},1,1,1).$$
3. Как прямое следствие определения ряда, значения полилогарифма при корнях p комплексных -го порядка из единицы задаются суммой Фурье :
   $$\operatorname {Li} _{s}(e^{2\pi im/p})=p^{-s}\sum _{k=1}^{p}e^{2\pi imk/p}\zeta (s,{\tfrac {k}{p}})\qquad (m=1,2,\dots ,p-1),$$
   где ζ – дзета-функция Гурвица . Для Re( s ) > 1, где Li _s (1) конечно, соотношение справедливо и при m = 0 или m = p . Хотя эта формула не так проста, как та, что подразумевается в более общей связи с дзета-функцией Гурвица, указанной ниже в разделе « Отношения с другими функциями» к неотрицательным целым значениям s , она имеет то преимущество, что применима и . Как обычно, соотношение можно инвертировать, чтобы выразить ζ( s , ^м ⁄ _p ) для любого m = 1, …, p как сумма Фурье Li _s (exp(2 πi ^к ⁄ _p )) над k = 1, …, p .

Связь с другими функциями

• При z = 1 полилогарифм сводится к дзета-функции Римана
  $$\operatorname {Li} _{s}(1)=\zeta (s)\qquad (\operatorname {Re} (s)>1).$$
• Полилогарифм связан с эта-функцией Дирихле и бета-функцией Дирихле :
  $$\operatorname {Li} _{s}(-1)=-\eta (s),$$
  где η ( s ) — эта-функция Дирихле. Для чисто мнимых аргументов мы имеем:
  $$\operatorname {Li} _{s}(\pm i)=-2^{-s}\eta (s)\pm i\beta (s),$$
  где β ( s ) — бета-функция Дирихле.
• Полилогарифм связан с полным интегралом Ферми – Дирака следующим образом:
  $$F_{s}(\mu )=-\operatorname {Li} _{s+1}(-e^{\mu }).$$
• Полилогарифм связан с полным интегралом Бозе – Эйнштейна следующим образом:
  $$G_{s}(\mu )=\operatorname {Li} _{s+1}(e^{\mu }).$$
• Полилогарифм является частным случаем неполной функции полилогарифма.
  $$\operatorname {Li} _{s}(z)=\operatorname {Li} _{s}(0,z).$$
• Полилогарифм является частным случаем трансцендента Лерха ( Эрдейи и др., 1981 , § 1.11-14).
  $$\operatorname {Li} _{s}(z)=z\Phi (z,s,1).$$
• Полилогарифм связан с дзета-функцией Гурвица соотношением:
  $$\operatorname {Li} _{s}(z)={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}\zeta \left(1-s,{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,{\frac {1}{2}}-{\ln(-z) \over {2\pi i}}\right)\right],$$
  это соотношение, однако, аннулируется при положительном целом s полюсами ; Γ гамма-функции (1 - s ) и при s = 0 полюсами обеих дзета-функций вывод этой формулы дан ниже в виде серий . С небольшой помощью функционального уравнения для дзета-функции Гурвица полилогарифм, следовательно, также связан с этой функцией посредством ( Жонкьер 1889 ):
  $$i^{-s}\operatorname {Li} _{s}(e^{2\pi ix})+i^{s}\operatorname {Li} _{s}(e^{-2\pi ix})={\frac {(2\pi )^{s}}{\Gamma (s)}}\zeta (1-s,x),$$
  какое соотношение выполняется для 0 ≤ Re( x ) < 1 , если Im( x ) ≥ 0 , и для 0 < Re( x ) ≤ 1, если Im( x ) < 0 . Эквивалентно, для всех комплексных s и для комплексных z ∉ (0, 1] формула обращения имеет следующий вид:
  $$\operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={\frac {(2\pi i)^{s}}{\Gamma (s)}}~\zeta \left(1-s,~{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right),$$
  и для всех комплексных s и для комплексных z ∉ (1, ∞)
  $$\operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right).$$
  Для z ∉ (0, ∞) имеем ln(− z ) = −ln(− ¹ ⁄ _z ) и оба выражения согласуются. Эти соотношения дают аналитическое продолжение полилогарифма за пределы круга сходимости | г | = 1 определяющего степенного ряда. (Соответствующее уравнение Жонкьера (1889 , уравнение 5) и Эрдейи и др. (1981 , § 1.11-16) неверно, если предположить, что главные ветви полилогарифма и логарифма используются одновременно.) См. следующее элемент для упрощенной формулы, когда s — целое число.
• Для положительных целых порядков полилогарифма s дзета-функция Гурвица ζ(1− s , x ) сводится к полиномам Бернулли ζ (1− n , x ) = −B _n ( x ) / n и формуле обращения Жонкера для n = 1 , 2, 3, … становится:
  $$\operatorname {Li} _{n}(e^{2\pi ix})+(-1)^{n}\operatorname {Li} _{n}(e^{-2\pi ix})=-{(2\pi i)^{n} \over n!}B_{n}(x),$$
  где снова 0 ≤ Re( x ) < 1, если Im( x ) ≥ 0, и 0 < Re( x ) ≤ 1, если Im( x ) < 0. При ограничении аргумента полилогарифма единичной окружностью Im( x ) = 0, левая часть этой формулы упрощается до 2 Re(Li _n ( e ^{2 πix} )) если n четно, и до 2 i Im(Li _n ( e ^{2 πix} )) если n нечетно. С другой стороны, для отрицательных целых порядков расхождение Γ( s ) означает для всех z , что ( Erdélyi et al. 1981 , § 1.11-17):
  $$\operatorname {Li} _{-n}(z)+(-1)^{n}\operatorname {Li} _{-n}(1/z)=0\qquad (n=1,2,3,\ldots ).$$
  В более общем смысле для n = 0, ±1, ±2, ±3,… :
  $${\begin{aligned}\operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)&=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)&(z\not \in ]0;1]),\\\operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)&=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right)&(z\not \in ~]1;\infty [),\end{aligned}}$$
  где оба выражения совпадают при z ∉ (0, ∞) . (Соответствующее уравнение Жонкьера (1889 , уравнение 1) и Эрдейи и др. (1981 , § 1.11-18) снова неверно.)
• Полилогарифм с чисто мнимым µ может быть выражен через функции Клаузена Ci _s (θ) и Si _s (θ) и наоборот ( Lewin 1958 , Ch. VII § 1.4; Abramowitz & Stegun 1972 , § 27.8):
  $$\operatorname {Li} _{s}(e^{\pm i\theta })=Ci_{s}(\theta )\pm iSi_{s}(\theta ).$$
• Обратный касательный интеграл Ti _s ( z ) ( Левин 1958 , гл. VII § 1.2) можно выразить через полилогарифмы:
  $$\operatorname {Ti} _{s}(z)={1 \over 2i}\left[\operatorname {Li} _{s}(iz)-\operatorname {Li} _{s}(-iz)\right].$$
  Это отношение, в частности, подразумевает:
  $$\operatorname {Ti} _{0}(z)={z \over 1+z^{2}},\quad \operatorname {Ti} _{1}(z)=\arctan z,\quad \operatorname {Ti} _{2}(z)=\int _{0}^{z}{\arctan t \over t}dt,\quad \ldots ~\quad \operatorname {Ti} _{n+1}(z)=\int _{0}^{z}{\frac {\operatorname {Ti} _{n}(t)}{t}}dt,$$
  что объясняет имя функции.
• χ Чи-функция Лежандра s ₍ z ) ( Lewin 1958 , Ch. VII § 1.1; Boersma & Dempsey 1992 ) может быть выражена через полилогарифмы:
  $$\chi _{s}(z)={\tfrac {1}{2}}\left[\operatorname {Li} _{s}(z)-\operatorname {Li} _{s}(-z)\right].$$
• Полилогарифм целого порядка можно выразить как обобщенную гипергеометрическую функцию :
  $${\begin{aligned}\operatorname {Li} _{n}(z)&=z_{n+1}F_{n}(1,1,\dots ,1;2,2,\dots ,2;z)&(n=0,1,2,\ldots ),\\\operatorname {Li} _{-n}(z)&=z_{n}F_{n-1}(2,2,\dots ,2;1,1,\dots ,1;z)&(n=1,2,3,\ldots )~.\end{aligned}}$$
• В терминах неполных дзета-функций или « функций Дебая » ( Абрамовиц и Стегун 1972 , § 27.1):
  $$Z_{n}(z)={1 \over (n-1)!}\int _{z}^{\infty }{t^{n-1} \over e^{t}-1}dt\qquad (n=1,2,3,\ldots ),$$
  полилогарифм Li _n ( z ) для положительного целого числа n может быть выражен как конечная сумма ( Wood 1992 , §16):
  $$\operatorname {Li} _{n}(e^{\mu })=\sum _{k=0}^{n-1}Z_{n-k}(-\mu ){\mu ^{k} \over k!}\qquad (n=1,2,3,\ldots ).$$
  Удивительно похожее выражение связывает «функции Дебая» Zn _: ( z ) с полилогарифмом
  $$Z_{n}(z)=\sum _{k=0}^{n-1}\operatorname {Li} _{n-k}(e^{-z}){z^{k} \over k!}\qquad (n=1,2,3,\ldots ).$$
• Используя ряд Ламберта , если $J_{s}(n)$ — функция Жордана , тогда
  $$\sum _{n=1}^{\infty }{\frac {z^{n}J_{-s}(n)}{1-z^{n}}}=\operatorname {Li} _{s}(z).$$

Интегральные представления

Любое из следующих интегральных представлений дает аналитическое продолжение полилогарифма за пределы круга сходимости | г | = 1 определяющего степенного ряда.

1. Полилогарифм можно выразить через интеграл распределения Бозе-Эйнштейна :
   $$\operatorname {Li} _{s}(z)={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1} \over e^{t}/z-1}dt.$$
   Это сходится для Re( s ) > 0 и всех z, за исключением z вещественного и ≥ 1. Полилогарифм в этом контексте иногда называют интегралом Бозе, но чаще — интегралом Бозе–Эйнштейна ( Dingle 1957a , Dingle, Arndt & Рой 1957 ). Аналогично полилогарифм можно выразить через интеграл от распределения Ферми – Дирака :
   $$-\operatorname {Li} _{s}(-z)={\frac {1}{\Gamma (s)}}\int _{0}^{\infty }{t^{s-1} \over e^{t}/z+1}dt.$$
   Это сходится для Re( s ) > 0 и всех z, кроме действительного z и ≤ −1. Полилогарифм в этом контексте иногда называют интегралом Ферми или интегралом Ферми – Дирака ( GSL 2010 , Dingle 1957b ). Эти представления легко проверяются разложением Тейлора подынтегральной функции по z и почленным интегрированием. Работы Дингла содержат подробные исследования обоих типов интегралов.Полилогарифм также связан с интегралом распределения Максвелла – Больцмана :
   $$\lim _{z\to 0}{\frac {\operatorname {Li} _{s}(z)}{z}}={1 \over \Gamma (s)}\int _{0}^{\infty }{t^{s-1}e^{-t}}dt=1.$$
   Это также дает асимптотическое поведение полилогарифма в окрестности начала координат.
2. Дополнительное интегральное представление применимо к Re( s ) <0 и ко всем z, кроме действительного z и ≥ 0:
   $$\operatorname {Li} _{s}(z)=\int _{0}^{\infty }{t^{-s}\sin[s\pi /2-t\ln(-z)] \over \sinh(\pi t)}dt.$$
   Этот интеграл следует из общей связи полилогарифма с дзета-функцией Гурвица ( см. выше ) и знакомого интегрального представления последней.
3. В общем случае полилогарифм может быть представлен контурным интегралом Ганкеля ( Whittaker & Watson 1927 , § 12.22, § 13.13), который расширяет представление Бозе-Эйнштейна до отрицательных порядков s . Пока подынтегрального выражения t = µ полюс не лежит на неотрицательной вещественной оси и s ≠ 1, 2, 3,…, мы имеем:
   $$\operatorname {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{(-t)^{s-1}} \over {e^{t-\mu }-1}}dt$$
   где H представляет контур Ганкеля. Подынтегральная функция имеет разрез по действительной оси от нуля до бесконечности, причем ось принадлежит нижней полуплоскости t . Интегрирование начинается в точке +∞ в верхней полуплоскости (Im( t ) > 0), огибает начало координат, не охватывая ни одного из полюсов t = µ + 2 kπi , и заканчивается в точке +∞ в нижней полуплоскости (Im( t ) < 0). В случае, когда µ вещественное и неотрицательное значение, мы можем просто вычесть вклад вложенного полюса t = µ :
   $$\operatorname {Li} _{s}(e^{\mu })=-{{\Gamma (1-s)} \over {2\pi i}}\oint _{H}{{(-t)^{s-1}} \over {e^{t-\mu }}-1}dt-2\pi iR$$
   где R – вычет полюса:
   $$R={i \over 2\pi }\Gamma (1-s)(-\mu )^{s-1}.$$
4. Когда формула Абеля-Плана применяется к определяющему ряду полилогарифма, получается интегральное представление типа Эрмита , справедливое для всех комплексных z и для всех комплексных s :
   $$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{\Gamma (1-s,-\ln z) \over (-\ln z)^{1-s}}+2z\int _{0}^{\infty }{\frac {\sin(s\arctan t-t\ln z)}{(1+t^{2})^{s/2}(e^{2\pi t}-1)}}dt$$
   где Γ — верхняя неполная гамма-функция . Все (но не часть) ln( z ) в этом выражении можно заменить на −ln( ¹ ⁄ _г ). Родственное представление, которое также справедливо для всех комплексных s ,
   $$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+z\int _{0}^{\infty }{\frac {\sin[s\arctan t-t\ln(-z)]}{(1+t^{2})^{s/2}\sinh(\pi t)}}dt,$$
   позволяет избежать использования неполной гамма-функции, но этот интеграл неверен для z на положительной вещественной оси, если Re( s ) ≤ 0. Это выражение находится путем записи 2 ^с Li _s (− z ) / (− z ) знак равно Φ( z ² , с , ¹ ⁄ ₂ ) - z Φ( z ² , s , 1), где Φ — трансцендент Лерха , и применение формулы Абеля–Планы к первому ряду Φ и дополнительной формулы, включающей 1 / ( e ^{2 балла} + 1) вместо 1 / ( e ^{2 балла} − 1) ко второй серии Φ.
5. Интеграл от полилогарифма можно выразить путем почленного интегрирования обычного геометрического ряда для $s\in \mathbb {N}$ as ( Borwein, Borwein & Girgensohn 1994 , §2, уравнение 4)
   $$\operatorname {Li} _{s+1}(z)={\frac {z\cdot (-1)^{s}}{s!}}\int _{0}^{1}{\frac {\log ^{s}(t)}{1-tz}}dt.$$

Представления серий

1. Как отмечалось выше в разделе об интегральных представлениях , интегральное представление полилогарифма Бозе – Эйнштейна может быть расширено до отрицательных порядков s посредством контурного интегрирования Ганкеля :
   $$\operatorname {Li} _{s}(e^{\mu })=-{\Gamma (1-s) \over 2\pi i}\oint _{H}{(-t)^{s-1} \over e^{t-\mu }-1}dt,$$
   где H — контур Ганкеля, s ≠ 1, 2, 3,…, а полюс подынтегрального выражения t = µ не лежит на неотрицательной вещественной оси. Контур . можно изменить так, чтобы он охватывал полюсы подынтегрального выражения при t − µ = 2 kπi , а интеграл можно вычислять как сумму вычетов ( Вуд 1992 , § 12, 13; Градштейн и Рыжик 1980 , § 9.553) ):
   $$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\sum _{k=-\infty }^{\infty }(2k\pi i-\mu )^{s-1}.$$
   Это будет справедливо для Re( s ) < 0 и всех µ, за исключением случая, когда e ^м = 1. Для 0 < Im( µ ) ≤ 2 π сумму можно разделить следующим образом:
   $$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\left[(-2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+{\mu \over {2\pi i}}\right)^{s-1}+(2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+1-{\mu \over {2\pi i}}\right)^{s-1}\right],$$
   где эти две серии теперь можно отождествить с дзета-функцией Гурвица :
   $$\operatorname {Li} _{s}(e^{\mu })={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}~\zeta \left(1-s,~{\mu \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,~1-{\mu \over {2\pi i}}\right)\right]\qquad (0<\operatorname {Im} (\mu )\leq 2\pi ).$$
   Это соотношение, которое уже было дано в связи с другими функциями выше, справедливо для всех комплексных s ≠ 0, 1, 2, 3,… и было впервые получено в ( Jonquière 1889 , уравнение 6).
2. Чтобы представить полилогарифм в виде степенного ряда относительно µ = 0, мы запишем ряд, полученный из контурного интеграла Ганкеля, как:
   $$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\Gamma (1-s)\sum _{h=1}^{\infty }\left[(-2h\pi i-\mu )^{s-1}+(2h\pi i-\mu )^{s-1}\right].$$
   Когда биномиальные степени в сумме разлагаются относительно µ = 0 и порядок суммирования меняется на обратный, сумму по h можно выразить в замкнутой форме:
   $$\operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\sum _{k=0}^{\infty }{\zeta (s-k) \over k!}\mu ^{k}.$$
   Этот результат справедлив для | | | < 2 π и благодаря аналитическому продолжению, обеспечиваемому дзета-функциями , для всех s ≠ 1, 2, 3, … . Если порядок является положительным целым числом, s = n , то и член с k = n - 1, и гамма-функция становятся бесконечными, хотя их сумма - нет. Получаем ( Wood 1992 , § 9; Gradshteyn & Ryzhik 1980 , § 9.554 ):
   $$\lim _{s\to k+1}\left[{\zeta (s-k) \over k!}\mu ^{k}+\Gamma (1-s)(-\mu )^{s-1}\right]={\mu ^{k} \over k!}\left[\sum _{h=1}^{k}{1 \over h}-\ln(-\mu )\right],$$
   где сумма по h обращается в нуль, если k = 0. Итак, для целых положительных порядков и для | | | < 2 π имеем ряд:
   $$\operatorname {Li} _{n}(e^{\mu })={\mu ^{n-1} \over (n-1)!}\left[H_{n-1}-\ln(-\mu )\right]+\sum _{k=0,k\neq n-1}^{\infty }{\zeta (n-k) \over k!}\mu ^{k},$$
   где H _n обозначает n-й гармоники номер :
   $$H_{n}=\sum _{h=1}^{n}{1 \over h},\qquad H_{0}=0.$$
   Условия задачи теперь содержат −ln(− µ ), которые при умножении на µ ^{п -1} , будет стремиться к нулю при µ → 0, за исключением n = 1. Это отражает тот факт, что Li _s ( z ) демонстрирует истинную логарифмическую особенность при s = 1 и z = 1, поскольку:
   $$\lim _{\mu \to 0}\Gamma (1-s)(-\mu )^{s-1}=0\qquad (\operatorname {Re} (s)>1).$$
   Для s, расходящиеся члены в разложении около µ близкого, но не равного положительному целому числу, можно ожидать, что = 0 вызовут вычислительные трудности ( Wood 1992 , § 9). Соответствующее разложение Эрдели ( Erdélyi et al. 1981 , § 1.11-15) по степеням ln( z ) неверно, если предположить, что главные ветви полилогарифма и логарифма используются одновременно, поскольку ln( ¹ ⁄ _z ) не равномерно равно −ln( z ).Для неположительных целых значений s дзета-функция ζ( s − k ) в разложении относительно µ = 0 сводится к числам Бернулли : ζ(− n − k ) = −B _{1+ n + k} / (1 + n + k ). Численная оценка Li _{− n} ( z ) с помощью этого ряда не страдает от эффектов отмены, которые конечные рациональные выражения, данные при определенных значениях выше, проявляют для больших n .
3. С помощью удостоверения
   $$1={1 \over \Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}dt\qquad (\operatorname {Re} (s)>0),$$
   Интегральное представление полилогарифма Бозе – Эйнштейна ( см. выше ) можно представить в виде:
   $$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{z \over 2\Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}\coth {t-\ln z \over 2}dt\qquad (\operatorname {Re} (s)>0).$$
   Заменив гиперболический котангенс двусторонним рядом,
   $$\coth {t-\ln z \over 2}=2\sum _{k=-\infty }^{\infty }{1 \over 2k\pi i+t-\ln z},$$
   затем меняя порядок интеграла и суммы и, наконец, отождествляя слагаемые с интегральным представлением верхней неполной гамма-функции , получаем:
   $$\operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+\sum _{k=-\infty }^{\infty }{\Gamma (1-s,2k\pi i-\ln z) \over (2k\pi i-\ln z)^{1-s}}.$$
   Как для двустороннего ряда этого результата, так и для гиперболического котангенса симметричные частичные суммы от − k _max до k _max сходятся безоговорочно при k _max → ∞. При условии, что суммирование выполняется симметрично, этот ряд для Li _s ( z ), таким образом, справедлив для всех комплексов s, а также для всех комплексов z .
4. Вводя явное выражение для чисел Стирлинга второго рода в конечную сумму полилогарифма неположительного целого порядка ( см. выше ), можно записать:
   $$\operatorname {Li} _{-n}(z)=\sum _{k=0}^{n}\left({-z \over 1-z}\right)^{k+1}\sum _{j=0}^{k}(-1)^{j+1}{k \choose j}(j+1)^{n}\qquad (n=0,1,2,\ldots ).$$
   Бесконечный ряд, полученный простым расширением внешнего суммирования до ∞ ( Guillera & Sondow 2008 , теорема 2.1):
   $$\operatorname {Li} _{s}(z)=\sum _{k=0}^{\infty }\left({-z \over 1-z}\right)^{k+1}~\sum _{j=0}^{k}(-1)^{j+1}{k \choose j}(j+1)^{-s},$$
   оказывается сходящимся к полилогарифму для всех комплексных s и для комплексных z с Re( z ) < ¹ ⁄ ₂ , что можно проверить для | ^{- г} ⁄ _{(1− z )} | < ¹ ⁄ ₂ , изменив порядок суммирования на обратный и используя:
   $$\sum _{k=j}^{\infty }{k \choose j}\left({-z \over 1-z}\right)^{k+1}=\left[\left({-z \over 1-z}\right)^{-1}-1\right]^{-j-1}=(-z)^{j+1}.$$
   Внутренние коэффициенты этих рядов могут быть выражены формулами , связанными с числами Стирлинга, включающими обобщенные гармонические числа . Например, см. Преобразования производящих функций , чтобы найти доказательства (ссылки на доказательства) следующих тождеств:
   $${\begin{aligned}\operatorname {Li} _{2}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{2}}\left(H_{j}^{2}+H_{j}^{(2)}\right){\frac {z^{j}}{(1-z)^{j+1}}}\\\operatorname {Li} _{3}(z)&=\sum _{j\geq 1}{\frac {(-1)^{j-1}}{6}}\left(H_{j}^{3}+3H_{j}H_{j}^{(2)}+2H_{j}^{(3)}\right){\frac {z^{j}}{(1-z)^{j+1}}}.\end{aligned}}$$
   Для остальных аргументов с Re( z ) < ¹ ⁄ ₂ результат следует аналитическим продолжением . Эта процедура эквивалентна применению преобразования Эйлера к ряду по z , определяющему полилогарифм.

Асимптотические разложения

Для | г | ≫ 1, полилогарифм можно разложить в асимптотический ряд по ln(− z ):

$$\operatorname {Li} _{s}(z)={\pm i\pi \over \Gamma (s)}[\ln(-z)\pm i\pi ]^{s-1}-\sum _{k=0}^{\infty }(-1)^{k}(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)\pm i\pi ]^{s-2k} \over \Gamma (s+1-2k)},$$

$$\operatorname {Li} _{s}(z)=\sum _{k=0}^{\infty }(-1)^{k}(1-2^{1-2k})(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)]^{s-2k} \over \Gamma (s+1-2k)},$$

где B _{2 k} — числа Бернулли . Обе версии верны для всех s и любого arg( z ). Как обычно, суммирование следует прекратить, когда члены начнут расти по величине. Для отрицательного целого числа s разложения полностью исчезают; для неотрицательного целого числа s они обрываются после конечного числа членов. Вуд (1992 , § 11) описывает метод получения этих рядов из интегрального представления Бозе–Эйнштейна (его уравнение 11.2 для Li _s ( e ^м ) требует −2 π < Im( µ ) ≤ 0).

Ограничивающее поведение

Следующие ограничения являются результатом различных представлений полилогарифма ( Wood 1992 , § 22):

$$\operatorname {Li} _{s}(z)\sim _{|z|\to 0}z$$

$$\operatorname {Li} _{s}(e^{\mu })\sim _{|\mu |\to 0}\Gamma (1-s)(-\mu )^{s-1}\qquad (\operatorname {Re} (s)<1)$$

$$\operatorname {Li} _{s}(\pm e^{\mu })\sim _{\operatorname {Re} (\mu )\to \infty }-{\mu ^{s} \over \Gamma (s+1)}\qquad (s\neq -1,-2,-3,\ldots )$$

$$\operatorname {Li} _{-n}(e^{\mu })\sim _{\operatorname {Re} (\mu )\to \infty }-(-1)^{n}e^{-\mu }\qquad (n=1,2,3,\ldots )$$

$$\operatorname {Li} _{s}(z)\sim _{\operatorname {Re} (s)\to \infty }z$$

$$\operatorname {Li} _{s}(e^{\mu })\sim _{\operatorname {Re} (s)\to -\infty }\Gamma (1-s)(-\mu )^{s-1}\qquad (-\pi <\operatorname {Im} (\mu )<\pi )$$

$$\operatorname {Li} _{s}(-e^{\mu })\sim _{\operatorname {Re} (s)\to -\infty }\Gamma (1-s)\left[(-\mu -i\pi )^{s-1}+(-\mu +i\pi )^{s-1}\right]\qquad (\operatorname {Im} (\mu )=0)$$

Первый предел Вуда для Re( µ ) → ∞ был исправлен в соответствии с его уравнением 11.3. Предел для Re( s ) → −∞ следует из общей связи полилогарифма с дзета-функцией Гурвица ( см. выше ).

Дилогарифм

Основная статья: Дилогарифм

Дилогарифм — это полилогарифм порядка s = 2. Альтернативное интегральное выражение дилогарифма для произвольного комплексного аргумента z : ( Abramowitz & Stegun 1972 , § 27.7):

$$\operatorname {Li} _{2}(z)=-\int _{0}^{z}{\ln(1-t) \over t}dt=-\int _{0}^{1}{\ln(1-zt) \over t}dt.$$

Источником путаницы является то, что некоторые системы компьютерной алгебры определяют дилогарифм как dilog( z ) = Li ₂ (1− z ).

В случае действительного z ≥ 1 первое интегральное выражение для дилогарифма можно записать как

$$\operatorname {Li} _{2}(z)={\frac {\pi ^{2}}{6}}-\int _{1}^{z}{\ln(t-1) \over t}dt-i\pi \ln z$$

откуда, разлагая ln( t −1) и интегрируя почленно, получаем

$$\operatorname {Li} _{2}(z)={\frac {\pi ^{2}}{3}}-{\frac {1}{2}}(\ln z)^{2}-\sum _{k=1}^{\infty }{1 \over k^{2}z^{k}}-i\pi \ln z\qquad (z\geq 1).$$

Тождество Абеля . для дилогарифма определяется выражением ( Абель 1881 )

$$\operatorname {Li} _{2}\left({\frac {x}{1-y}}\right)+\operatorname {Li} _{2}\left({\frac {y}{1-x}}\right)-\operatorname {Li} _{2}\left({\frac {xy}{(1-x)(1-y)}}\right)=\operatorname {Li} _{2}(x)+\operatorname {Li} _{2}(y)+\ln(1-x)\ln(1-y)$$

$$(\operatorname {Re} (x)\leq {\tfrac {1}{2}}\wedge \operatorname {Re} (y)\leq {\tfrac {1}{2}}\vee \operatorname {Im} (x)>0\wedge \operatorname {Im} (y)>0\vee \operatorname {Im} (x)<0\wedge \operatorname {Im} (y)<0\vee \ldots ).$$

Сразу видно, что это справедливо либо для x = 0, либо для y = 0, а затем для общих рассуждений легко проверяется дифференцированием ∂/∂ x ∂/∂ y . При y = 1− x тождество сводится к Эйлера отражения формуле

$$\operatorname {Li} _{2}\left(x\right)+\operatorname {Li} _{2}\left(1-x\right)={\frac {1}{6}}\pi ^{2}-\ln(x)\ln(1-x),$$

где Li ₂ (1) = ζ(2) = ¹ ⁄ ₆ π ² использовался, и x может принимать любое комплексное значение.

В терминах новых переменных u = x /(1− y ), v = y /(1− x ) тождество Абеля имеет вид

$$\operatorname {Li} _{2}(u)+\operatorname {Li} _{2}(v)-\operatorname {Li} _{2}(uv)=\operatorname {Li} _{2}\left({\frac {u-uv}{1-uv}}\right)+\operatorname {Li} _{2}\left({\frac {v-uv}{1-uv}}\right)+\ln \left({\frac {1-u}{1-uv}}\right)\ln \left({\frac {1-v}{1-uv}}\right),$$

что соответствует тождеству пятиугольника , данному в ( Rogers 1907 ).

Из тождества Абеля для x = y = 1− z и соотношения квадратов мы получаем Ландена тождество

$$\operatorname {Li} _{2}(1-z)+\operatorname {Li} _{2}\left(1-{\frac {1}{z}}\right)=-{\frac {1}{2}}(\ln z)^{2}\qquad (z\not \in ~]-\infty ;0]),$$

и применив формулу отражения к каждому дилогарифму, находим формулу обращения

$$\operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)=-{\tfrac {1}{6}}\pi ^{2}-{\tfrac {1}{2}}[\ln(-z)]^{2}\qquad (z\not \in [0;1[),$$

и для действительного z ≥ 1 также

$$\operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)={\tfrac {1}{3}}\pi ^{2}-{\tfrac {1}{2}}(\ln z)^{2}-i\pi \ln z.$$

Известные оценки дилогарифма в замкнутой форме при специальных аргументах собраны в таблице ниже. Аргументы в первом столбце связаны отражением x ↔ 1− x или инверсией x ↔. ¹ ⁄ _x либо x = 0, либо x = -1; все аргументы в третьем столбце связаны между собой этими операциями.

Максимон (2003) обсуждает ссылки 17-19 веков. Формула отражения уже была опубликована Ланденом в 1760 году, до ее появления в книге Эйлера 1768 года ( Максимон 2003 , § 10); эквивалент личности Абеля был уже опубликован Спенсом в 1809 году, до того, как Абель написал свою рукопись в 1826 году ( Zagier 1989 , § 2). Обозначение билогарифмической функции было введено Карлом Йоханом Даниэльссоном Хиллом (профессором из Лунда, Швеция) в 1828 году ( Maximon 2003 , § 10). Дон Загер ( 1989 ) заметил, что дилогарифм — единственная математическая функция, обладающая чувством юмора.

Особые значения дилогарифма

$x$	$\operatorname {Li} _{2}(x)$	$x$	$\operatorname {Li} _{2}(x)$
$-1$	$-{\tfrac {1}{12}}\pi ^{2}$	$-\phi$	$-{\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi$
$0$	$0$	$-1/\phi$	$-{\tfrac {1}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}\phi$
${\tfrac {1}{2}}$	${\tfrac {1}{12}}\pi ^{2}-{\tfrac {1}{2}}\ln ^{2}2$	$1/\phi ^{2}$	${\tfrac {1}{15}}\pi ^{2}-\ln ^{2}\phi$
$1$	${\tfrac {1}{6}}\pi ^{2}$	$1/\phi$	${\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\phi$
$2$	${\tfrac {1}{4}}\pi ^{2}-\pi i\ln 2$	$\phi$	${\tfrac {11}{15}}\pi ^{2}+{\tfrac {1}{2}}\ln ^{2}(-1/\phi )$
		$\phi ^{2}$	$-{\tfrac {11}{15}}\pi ^{2}-\ln ^{2}(-\phi )$

Здесь $\phi ={\tfrac {1}{2}}({\sqrt {5}}+1)$ обозначает золотое сечение .

Лестницы полилогарифмов

Леонард Левин обнаружил замечательное и широкое обобщение ряда классических соотношений полилогарифма для специальных значений. Сейчас они называются полилогарифмическими лестницами . Определять $\rho ={\tfrac {1}{2}}({\sqrt {5}}-1)$ как обратную величину золотого сечения . Тогда два простых примера дилогарифмических лестниц:

$$\operatorname {Li} _{2}(\rho ^{6})=4\operatorname {Li} _{2}(\rho ^{3})+3\operatorname {Li} _{2}(\rho ^{2})-6\operatorname {Li} _{2}(\rho )+{\tfrac {7}{30}}\pi ^{2}$$

данный Коксетером ( 1935 ) и

$$\operatorname {Li} _{2}(\rho )={\tfrac {1}{10}}\pi ^{2}-\ln ^{2}\rho$$

предоставлено Ланденом . Лестницы полилогарифмов естественным образом и глубоко встречаются в K-теории и алгебраической геометрии . Лестницы полилогарифмов обеспечивают основу для быстрых вычислений различных математических констант с помощью алгоритма BBP ( Bailey, Borwein & Plouffe 1997 ).

Monodromy

Полилогарифм имеет две точки ветвления ; одна при z = 1, а другая при z = 0. Вторая точка ветвления при z = 0 не видна на основном листе полилогарифма; он становится видимым только тогда, когда функция аналитически продолжается на другие ее листы. Группа монодромии полилогарифма состоит из гомотопических классов петель, обвивающих две точки ветвления. Обозначая эти два через m ₀ и m ₁ , группа монодромии имеет групповое представление

$$\langle m_{0},m_{1}\vert w=m_{0}m_{1}m_{0}^{-1}m_{1}^{-1},wm_{1}=m_{1}w\rangle .$$

Для частного случая дилогарифма также имеет место wm ₀ = m ₀ w , и группа монодромии становится группой Гейзенберга (отождествляя m ₀ , m ₁ и w с x , y , z ) ( Вепстас 2008 ).

Ссылки

• Абель, Нью-Хэмпшир (1881) [1826]. «Примечание к функции $\scriptstyle \psi x=x+{\frac {x^{2}}{2^{2}}}+{\frac {x^{3}}{3^{2}}}+\cdots +{\frac {x^{n}}{n^{2}}}+\cdots$» (PDF) . In Sylow, L.; Lie, S. (ред.). Œuvres complètes de Niels Henrik Abel - Nouvelle édition, Tome II (на французском языке). Christiania [Осло]: Grøndahl & Søn., стр. 189– 193. (Эта рукопись 1826 года была опубликована только посмертно.)
• Абрамовиц, М.; Стегун, Айова (1972). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Нью-Йорк: Dover Publications. ISBN  978-0-486-61272-0 .
• Апостол, ТМ (2010), «Полилогарифм» , Олвер, Фрэнк У.Дж .; Лозье, Дэниел М.; Буасверт, Рональд Ф.; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Бейли, DH ; Борвейн, ПБ ; Плуфф, С. (апрель 1997 г.). «О быстром вычислении различных полилогарифмических констант» (PDF) . Математика вычислений . 66 (218): 903–913. Бибкод : 1997MaCom..66..903B . дои : 10.1090/S0025-5718-97-00856-9 .
• Бейли, Д.Х.; Бродхерст, ди-джей (20 июня 1999 г.). «Лестница полилогарифмов семнадцатого порядка». arXiv : math.CA/9906134 .
• Берндт, Британская Колумбия (1994). Записные книжки Рамануджана, часть IV . Нью-Йорк: Springer-Verlag. стр. 323–326. ISBN  978-0-387-94109-7 .
• Боерсма, Дж . ; Демпси, JP (1992). «Об оценке хи-функции Лежандра» . Математика вычислений . 59 (199): 157–163. дои : 10.2307/2152987 . JSTOR   2152987 .
• Борвейн, Д. ; Борвейн, Дж. М. ; Гиргенсон, Р. (1995). «Явное вычисление сумм Эйлера» (PDF) . Труды Эдинбургского математического общества . Серия 2. 38 (2): 277–294. дои : 10.1017/S0013091500019088 .
• Борвейн, Дж. М.; Брэдли, DM; Бродхерст, диджей; Лисонек, П. (2001). «Особые значения кратных полилогарифмов». Труды Американского математического общества . 353 (3): 907–941. arXiv : математика/9910045 . дои : 10.1090/S0002-9947-00-02616-7 . S2CID   11373360 .
• Бродхерст, ди-джей (21 апреля 1996 г.). «О перечислении неприводимых k-кратных сумм Эйлера и их роли в теории узлов и теории поля». arXiv : hep-th/9604128 .
• Клуни, Дж. (1954). «О функциях Бозе-Эйнштейна». Труды Физического общества . Серия А. 67 (7): 632–636. Бибкод : 1954PPSA...67..632C . дои : 10.1088/0370-1298/67/7/308 .
• Коэн, Х.; Левин, Л.; Загер, Д. (1992). «Лестница полилогарифмов шестнадцатого порядка» (ПС) . Экспериментальная математика . 1 (1): 25–34.
• Коксетер, HSM (1935). «Функции Шлефли и Лобачевского». Ежеквартальный математический журнал . 6 (1): 13–29. Бибкод : 1935QJMat...6...13C . дои : 10.1093/qmath/os-6.1.13 . ЖФМ   61.0395.02 .
• Цвийович, Д.; Клиновски, Дж. (1997). «Разложения в непрерывные дроби для дзета-функции Римана и полилогарифмов» (PDF) . Труды Американского математического общества . 125 (9): 2543–2550. дои : 10.1090/S0002-9939-97-04102-6 .
• Цвийович, Д. (2007). «Новые интегральные представления функции полилогарифма». Труды Королевского общества А. 463 (2080): 897–905. arXiv : 0911.4452 . Бибкод : 2007RSPSA.463..897C . дои : 10.1098/rspa.2006.1794 . S2CID   115156743 .
• Дингл, РБ (1955). «Вычисление интегралов, содержащих параметр» . Прикладные научные исследования, раздел Б. 4 (1): 401–410. дои : 10.1007/BF02920017 . ISSN   0365-7140 .
• Дингл, РБ (1957a). «Интегралы Бозе-Эйнштейна ${\mathcal {B}}_{p}(\eta )=(p!)^{-1}\int \limits _{0}^{\infty }{\varepsilon ^{p}(e^{\varepsilon -\eta }-1})^{-1}d\varepsilon$« . Прикладные научные исследования, раздел B. 6 ( 1): 240–244. doi : 10.1007/BF02920380 . ISSN   0365-7140 .
• Дингл, РБ; Арндт, Дорин; Рой, СК (1957). «Интегралы ${\mathfrak {A}}_{p}(x)=(p!)^{-1}\int \limits _{0}^{\infty }{\varepsilon ^{p}(\varepsilon +x})^{-1}e^{-\varepsilon }d\varepsilon$ и ${\mathfrak {B}}_{p}(x)=(p!)^{-1}\int \limits _{0}^{\infty }{\varepsilon ^{p}(\varepsilon +x})^{-2}e^{-\varepsilon }d\varepsilon$ и их табулирование» . Прикладные научные исследования, раздел B. 6 ( 1): 144–154. doi : 10.1007/BF02920371 . ISSN   0365-7140 .
• Дингл, РБ (1957b). «Интегралы Ферми-Дирака ${\mathcal {F}}_{p}(\eta )=(p!)^{-1}\int \limits _{0}^{\infty }{\varepsilon ^{p}(e^{\varepsilon -\eta }+1})^{-1}d\varepsilon$« . Прикладные научные исследования, раздел B. 6 ( 1): 225–239. doi : 10.1007/BF02920379 . ISSN   0365-7140 .
• Эрдели, А. ; Магнус, В.; Оберхеттингер, Ф.; Трикоми, Ф.Г. (1981). Высшие трансцендентные функции, Том 1 (PDF) . Малабар, Флорида: RE Krieger Publishing. ISBN  978-0-89874-206-0 . (это перепечатка оригинала МакГроу-Хилла 1953 года.)
• Форнберг, Б.; Кёлбиг, К.С. (1975). «Комплексные нули функции Жонкьера или полилогарифма» . Математика вычислений . 29 (130): 582–599. дои : 10.2307/2005579 . JSTOR   2005579 .
• Научная библиотека GNU (2010). «Справочное руководство» . Проверено 13 июня 2010 г.
• Градштейн Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Героним Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015) [октябрь 2014 г.]. «9.553.». В Цвиллингере, Дэниел; Молл, Виктор Гюго (ред.). Таблица интегралов, рядов и произведений . Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. с. 1050. ИСБН  978-0-12-384933-5 . LCCN   2014010276 .
• Гильера, Дж.; Сондоу, Дж. (2008). «Двойные интегралы и бесконечные произведения для некоторых классических констант через аналитическое продолжение трансцендента Лерха». Журнал Рамануджана . 16 (3): 247–270. arXiv : math.NT/0506319 . дои : 10.1007/s11139-007-9102-0 . S2CID   119131640 .
• Хейн, Р.М. (25 марта 1992 г.). «Классические полилогарифмы». arXiv : alg-geom/9202022 .
• Янке, Э.; Эмде, Ф. (1945). Таблицы функций с формулами и кривыми (4-е изд.). Нью-Йорк: Dover Publications.
• Жонкьер, А. (1889). «Примечание к сериалу $\scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{s}}}$ bsmf.392 (PDF) . Bulletin de la Société Mathématique de France (на французском языке). 17 : 142–152. doi : 10.24033/ . JFM   21.0246.02 .
• Кёльбиг, Канзас; Миньяко, JA; Ремидди, Э. (1970). «Об обобщенных полилогарифмах Нильсена и их численном вычислении» . КУСОЧЕК . 10 : 38–74. дои : 10.1007/BF01940890 . S2CID   119672619 .
• Кириллов, АН (1995). «Дилогарифмические тождества». Приложение «Прогресс теоретической физики» . 118 : 61–142. arXiv : hep-th/9408113 . Бибкод : 1995ПТПС.118...61К . дои : 10.1143/PTPS.118.61 . S2CID   119177149 .
• Левин, Л. (1958). Дилогарифмы и ассоциированные функции . Лондон: Макдональд. МР   0105524 .
• Левин, Л. (1981). Полилогарифмы и связанные с ними функции . Нью-Йорк: Северная Голландия. ISBN  978-0-444-00550-2 .
• Левин, Л., изд. (1991). Структурные свойства полилогарифмов . Математические обзоры и монографии. Том. 37. Провиденс, Род-Айленд: Амер. Математика. Соц. ISBN  978-0-8218-1634-9 .
• Маркман, Б. (1965). «Дзета-функция Римана». КУСОЧЕК . 5 : 138–141.
• Максимон, LC (2003). «Функция дилогарифма для сложного аргумента». Труды Королевского общества А. 459 (2039): 2807–2819. Бибкод : 2003RSPSA.459.2807M . дои : 10.1098/rspa.2003.1156 . S2CID   122271244 .
• Макдугалл, Дж.; Стоунер, ЕС (1938). «Вычисление функций Ферми-Дирака» . Философские труды Королевского общества А. 237 (773): 67–104. Бибкод : 1938РСПТА.237...67М . дои : 10.1098/rsta.1938.0004 . ЖФМ   64.1500.04 .
• Нильсен, Н. (1909). «Дилогарифм Эйлера и его обобщения. Монография». Nova Acta Leopoldina (на немецком языке). ХС (3). Галле – Лейпциг, Германия: Императорско-Леопольдинско-Каролинская Немецкая академия естествознания: 121–212. ЖФМ   40.0478.01 .
• Прудников А.П.; Маричев О.И.; Брычков, Ю.А. (1990). Интегралы и ряды, Vol. 3: Дополнительные специальные функции . Ньюарк, Нью-Джерси: Гордон и Брич. ISBN  978-2-88124-682-1 . (см. § 1.2, «Обобщенная дзета-функция, полиномы Бернулли, полиномы Эйлера и полилогарифмы», стр. 23.)
• Робинсон, Дж. Э. (1951). «Заметка об интегральных функциях Бозе-Эйнштейна». Физический обзор . Серия 2. 83 (3): 678–679. Бибкод : 1951PhRv...83..678R . дои : 10.1103/PhysRev.83.678 .
• Роджерс, LJ (1907). «О теоремах суммы функций, связанных с рядом $\scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{2}}}$ 10.1112/plms / Труды Лондонского математического общества (2) . 4 (1): 169–189. doi : s2-4.1.169 . JFM   37.0428.03 .
• Шредингер, Э. (1952). Статистическая термодинамика (2-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета.
• Трусделл, К. (1945). «О функции, встречающейся в теории строения полимеров». Анналы математики . Вторая серия. 46 (1): 144–157. дои : 10.2307/1969153 . JSTOR   1969153 .
• Вепстас, Л. (2008). «Эффективный алгоритм ускорения сходимости колебательных рядов, полезный для вычисления полилогарифмов и дзета-функций Гурвица». Численные алгоритмы . 47 (3): 211–252. arXiv : math.CA/0702243 . Бибкод : 2008NuAlg..47..211В . дои : 10.1007/s11075-007-9153-8 . S2CID   15131811 .
• Уиттакер, ET ; Уотсон, Дж. Н. (1927). Курс современного анализа (4-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. (это издание много раз переиздавалось, в мягкой обложке 1996 г.) ISBN   0-521-09189-6 .)
• Виртингер, В. (1905). «Об особой серии Дирихле». Журнал чистой и прикладной математики (на немецком языке). 1905 (129): 214–219. дои : 10.1515/crll.1905.129.214 . ЯФМ   37.0434.01 . S2CID   199545536 .
• Вуд, округ Колумбия (июнь 1992 г.). «Вычисление полилогарифмов. Технический отчет 15-92*» (ПС) . Кентербери, Великобритания: Вычислительная лаборатория Кентского университета . Проверено 1 ноября 2005 г.
• Загер, Д. (1989). «Функция дилогарифма в геометрии и теории чисел». Теория чисел и смежные темы: доклады, представленные на коллоквиуме Рамануджана, Бомбей, 1988 г. Исследования по математике. Том. 12. Бомбей: Институт фундаментальных исследований Таты и издательство Оксфордского университета. стр. 231–249. ISBN  0-19-562367-3 . (также появился как «Замечательный дилогарифм» в Journal of Mathematical and Physical Sciences 22 (1988), стр. 131–145, а также в главе I ( Zagier 2007 ).)
• Загер, Д. (2007). «Функция дилогарифма» (PDF) . В Картье, ЧП; и др. (ред.). Границы теории чисел, физики и геометрии II - О конформных теориях поля, дискретных группах и перенормировке . Берлин: Springer-Verlag. стр. 3–65. ISBN  978-3-540-30307-7 .

Внешние ссылки

• Вайсштейн, Эрик В. «Полилогарифм» . Математический мир .
• Вайсштейн, Эрик В. «Дилогарифм» . Математический мир .
• Алгоритмы в аналитической теории чисел обеспечивают реализацию произвольной точности на основе GMP и под лицензией GPL .