функция Гудермана

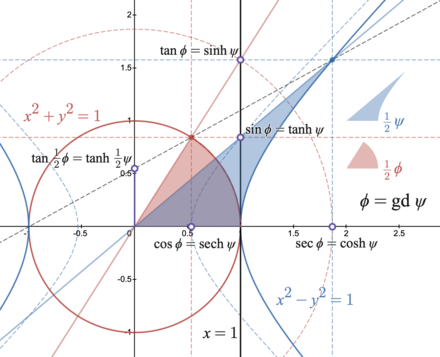
Функция Гудермана связывает площадь кругового сектора с площадью гиперболического сектора посредством общей стереографической проекции . Если удвоенная площадь синего гиперболического сектора равна ψ , то удвоенная площадь красного кругового сектора равна ψ = gd ψ . Двойная площадь фиолетового треугольника равна стереографической проекции s = tan. 1/2 ​ = φ рыбный 1/2 ​ ​ ψ . Синяя точка имеет координаты (cosh ψ , sinh ψ ) . Красная точка имеет координаты (cos φ , sin φ ). Фиолетовая точка имеет координаты (0, s ).

График функции Гудермана.

График обратной функции Гудермана.

В математике функция Гудермана связывает гиперболическую угловую меру. ${\textstyle \psi }$ до окружного угла меры ${\textstyle \phi }$ называемый гудерманианом ​ ${\textstyle \psi }$ и обозначил ${\textstyle \operatorname {gd} \psi }$. Функция Гудермана обнаруживает тесную связь между круговыми функциями и гиперболическими функциями . Он был введен в 1760-х годах Иоганном Генрихом Ламбертом и позже назван в честь Кристофа Гудермана, который также описал взаимосвязь между круговыми и гиперболическими функциями в 1830 году. Гудерманниан иногда называют гиперболической амплитудой как предельный случай эллиптической амплитуды Якоби. ${\textstyle \operatorname {am} (\psi ,m)}$ когда параметр ${\textstyle m=1.}$

Действительная функция Гудермана обычно определяется для ${\textstyle -\infty <\psi <\infty }$ быть интегралом гиперболического секанса

$\phi =\operatorname {gd} \psi \equiv \int _{0}^{\psi }\operatorname {sech} t\,\mathrm {d} t=\operatorname {arctan} (\sinh \psi ).$

Действительная обратная функция Гудермана может быть определена для ${\textstyle -{\tfrac {1}{2}}\pi <\phi <{\tfrac {1}{2}}\pi }$ как интеграл от (кругового) секущего

$\psi =\operatorname {gd} ^{-1}\phi =\int _{0}^{\phi }\operatorname {sec} t\,\mathrm {d} t=\operatorname {arsinh} (\tan \phi ).$

Гиперболическая мера угла $\psi =\operatorname {gd} ^{-1}\phi$ называется антигудерманианом ​ $\phi$ или ламбертиан иногда $\phi$, обозначенный $\psi =\operatorname {lam} \phi .$ В контексте геодезии и навигации по широте ${\textstyle \phi }$, $k\operatorname {gd} ^{-1}\phi$ (масштабируется произвольной константой ${\textstyle k}$) исторически называли частью меридиональной $\phi$ ( Французский : широта круассана ). Это вертикальная координата проекции Меркатора .

Две угловые меры ${\textstyle \phi }$ и ${\textstyle \psi }$ связаны общей стереографической проекцией

$s=\tan {\tfrac {1}{2}}\phi =\tanh {\tfrac {1}{2}}\psi ,$

и эта идентичность может служить альтернативным определением ${\textstyle \operatorname {gd} }$ и ${\textstyle \operatorname {gd} ^{-1}}$ действует на всей комплексной плоскости :

${\begin{aligned}\operatorname {gd} \psi &={2\arctan }{\bigl (}\tanh {\tfrac {1}{2}}\psi \,{\bigr )},\\[5mu]\operatorname {gd} ^{-1}\phi &={2\operatorname {artanh} }{\bigl (}\tan {\tfrac {1}{2}}\phi \,{\bigr )}.\end{aligned}}$

-

Мы можем оценить интеграл гиперболического секанса, используя стереографическую проекцию ( гиперболическую полукасательную ) как замену переменных :

${\begin{aligned}\operatorname {gd} \psi &\equiv \int _{0}^{\psi }{\frac {1}{\operatorname {cosh} t}}\mathrm {d} t=\int _{0}^{\tanh {\frac {1}{2}}\psi }{\frac {1-u^{2}}{1+u^{2}}}{\frac {2\,\mathrm {d} u}{1-u^{2}}}\qquad {\bigl (}u=\tanh {\tfrac {1}{2}}t{\bigr )}\\[8mu]&=2\int _{0}^{\tanh {\frac {1}{2}}\psi }{\frac {1}{1+u^{2}}}\mathrm {d} u={2\arctan }{\bigl (}\tanh {\tfrac {1}{2}}\psi \,{\bigr )},\\[5mu]\tan {\tfrac {1}{2}}{\operatorname {gd} \psi }&=\tanh {\tfrac {1}{2}}\psi .\end{aligned}}$

Сдача в аренду ${\textstyle \phi =\operatorname {gd} \psi }$ и ${\textstyle s=\tan {\tfrac {1}{2}}\phi =\tanh {\tfrac {1}{2}}\psi }$ мы можем вывести ряд тождеств между гиперболическими функциями ${\textstyle \psi }$ и круговые функции ${\textstyle \phi .}$

Identities related to the Gudermannian function represented graphically.

${\begin{aligned}s&=\tan {\tfrac {1}{2}}\phi =\tanh {\tfrac {1}{2}}\psi ,\\[6mu]{\frac {2s}{1+s^{2}}}&=\sin \phi =\tanh \psi ,\quad &{\frac {1+s^{2}}{2s}}&=\csc \phi =\coth \psi ,\\[10mu]{\frac {1-s^{2}}{1+s^{2}}}&=\cos \phi =\operatorname {sech} \psi ,\quad &{\frac {1+s^{2}}{1-s^{2}}}&=\sec \phi =\cosh \psi ,\\[10mu]{\frac {2s}{1-s^{2}}}&=\tan \phi =\sinh \psi ,\quad &{\frac {1-s^{2}}{2s}}&=\cot \phi =\operatorname {csch} \psi .\\[8mu]\end{aligned}}$

Они обычно используются в качестве выражений для $\operatorname {gd}$ и $\operatorname {gd} ^{-1}$ для реальных значений $\psi$ и $\phi$ с $|\phi |<{\tfrac {1}{2}}\pi .$ Например, численно корректные формулы

${\begin{aligned}\operatorname {gd} \psi &=\operatorname {arctan} (\sinh \psi ),\\[6mu]\operatorname {gd} ^{-1}\phi &=\operatorname {arsinh} (\tan \phi ).\end{aligned}}$

(Обратите внимание, для $|\phi |>{\tfrac {1}{2}}\pi$ а для сложных аргументов необходимо проявлять осторожность при выборе ветвей обратных функций.)

Мы также можем выразить ${\textstyle \psi }$ и ${\textstyle \phi }$ с точки зрения ${\textstyle s\colon }$

${\begin{aligned}2\arctan s&=\phi =\operatorname {gd} \psi ,\\[6mu]2\operatorname {artanh} s&=\operatorname {gd} ^{-1}\phi =\psi .\\[6mu]\end{aligned}}$

Если мы расширим ${\textstyle \tan {\tfrac {1}{2}}}$ и ${\textstyle \tanh {\tfrac {1}{2}}}$ с точки зрения экспоненты , то мы видим, что ${\textstyle s,}$ $\exp \phi i,$ и $\exp \psi$ все преобразования Мёбиуса друг друга (в частности, вращения сферы Римана ):

${\begin{aligned}s&=i{\frac {1-e^{\phi i}}{1+e^{\phi i}}}={\frac {e^{\psi }-1}{e^{\psi }+1}},\\[10mu]i{\frac {s-i}{s+i}}&=\exp \phi i\quad ={\frac {e^{\psi }-i}{e^{\psi }+i}},\\[10mu]{\frac {1+s}{1-s}}&=i{\frac {i+e^{\phi i}}{i-e^{\phi i}}}\,=\exp \psi .\end{aligned}}$

Для реальных значений ${\textstyle \psi }$ и ${\textstyle \phi }$ с $|\phi |<{\tfrac {1}{2}}\pi$, эти преобразования Мёбиуса можно записать в терминах тригонометрических функций несколькими способами:

${\begin{aligned}\exp \psi &=\sec \phi +\tan \phi =\tan {\tfrac {1}{2}}{\bigl (}{\tfrac {1}{2}}\pi +\phi {\bigr )}\\[6mu]&={\frac {1+\tan {\tfrac {1}{2}}\phi }{1-\tan {\tfrac {1}{2}}\phi }}={\sqrt {\frac {1+\sin \phi }{1-\sin \phi }}},\\[12mu]\exp \phi i&=\operatorname {sech} \psi +i\tanh \psi =\tanh {\tfrac {1}{2}}{\bigl (}{-{\tfrac {1}{2}}}\pi i+\psi {\bigr )}\\[6mu]&={\frac {1+i\tanh {\tfrac {1}{2}}\psi }{1-i\tanh {\tfrac {1}{2}}\psi }}={\sqrt {\frac {1+i\sinh \psi }{1-i\sinh \psi }}}.\end{aligned}}$

Они дают дальнейшие выражения для $\operatorname {gd}$ и $\operatorname {gd} ^{-1}$ для реальных споров с $|\phi |<{\tfrac {1}{2}}\pi .$ Например,

${\begin{aligned}\operatorname {gd} \psi &=2\arctan e^{\psi }-{\tfrac {1}{2}}\pi ,\\[6mu]\operatorname {gd} ^{-1}\phi &=\log(\sec \phi +\tan \phi ).\end{aligned}}$

Комплексные значения

Функция Гудермана z ↦ gd z представляет собой конформное отображение бесконечной полосы в бесконечную полосу. Его можно разбить на две части: карта z ↦ tanh 1/2 одной бесконечной из z полосы в комплексный единичный круг и отображение ζ ↦ 2 arctan ζ из диска в другую бесконечную полосу.

Как функция комплексной переменной , ${\textstyle z\mapsto w=\operatorname {gd} z}$ конформно отображает бесконечную полосу ${\textstyle \left|\operatorname {Im} z\right|\leq {\tfrac {1}{2}}\pi }$ до бесконечной полосы ${\textstyle \left|\operatorname {Re} w\right|\leq {\tfrac {1}{2}}\pi ,}$ пока ${\textstyle w\mapsto z=\operatorname {gd} ^{-1}w}$ конформно отображает бесконечную полосу ${\textstyle \left|\operatorname {Re} w\right|\leq {\tfrac {1}{2}}\pi }$ до бесконечной полосы ${\textstyle \left|\operatorname {Im} z\right|\leq {\tfrac {1}{2}}\pi .}$

продолжено размышлениями Аналитически на всю сложную плоскость, ${\textstyle z\mapsto w=\operatorname {gd} z}$ является периодической функцией периода ${\textstyle 2\pi i}$ который отправляет любую бесконечную полосу «высоты» ${\textstyle 2\pi i}$ на полосу ${\textstyle -\pi <\operatorname {Re} w\leq \pi .}$ Аналогично, распространяется на всю комплексную плоскость: ${\textstyle w\mapsto z=\operatorname {gd} ^{-1}w}$ является периодической функцией периода ${\textstyle 2\pi }$ который отправляет любую бесконечную полосу «ширины» ${\textstyle 2\pi }$ на полосу ${\textstyle -\pi <\operatorname {Im} z\leq \pi .}$ Для всех точек комплексной плоскости эти функции можно правильно записать как:

${\begin{aligned}\operatorname {gd} z&={2\arctan }{\bigl (}\tanh {\tfrac {1}{2}}z\,{\bigr )},\\[5mu]\operatorname {gd} ^{-1}w&={2\operatorname {artanh} }{\bigl (}\tan {\tfrac {1}{2}}w\,{\bigr )}.\end{aligned}}$

Для ${\textstyle \operatorname {gd} }$ и ${\textstyle \operatorname {gd} ^{-1}}$ чтобы функции оставались обратимыми в этих расширенных областях, мы могли бы рассматривать каждую из них как многозначную функцию (возможно, ${\textstyle \operatorname {Gd} }$ и ${\textstyle \operatorname {Gd} ^{-1}}$, с ${\textstyle \operatorname {gd} }$ и ${\textstyle \operatorname {gd} ^{-1}}$ главная ветвь ) или рассматривать их области и кообласти как римановы поверхности .

Если ${\textstyle u+iv=\operatorname {gd} (x+iy),}$ тогда действительная и мнимая составляющие ${\textstyle u}$ и ${\textstyle v}$ можно найти:

$\tan u={\frac {\sinh x}{\cos y}},\quad \tanh v={\frac {\sin y}{\cosh x}}.$

(При практической реализации обязательно используйте арктангенс с двумя аргументами , ${\textstyle u=\operatorname {atan2} (\sinh x,\cos y)}$.)

Аналогично, если ${\textstyle x+iy=\operatorname {gd} ^{-1}(u+iv),}$ затем компоненты ${\textstyle x}$ и ${\textstyle y}$ можно найти:

$\tanh x={\frac {\sin u}{\cosh v}},\quad \tan y={\frac {\sinh v}{\cos u}}.$

Умножение их вместе показывает дополнительную идентичность

$\tanh x\,\tan y=\tan u\,\tanh v.$

Симметрии

Эти две функции можно рассматривать как вращение или отражение друг друга, с аналогичными отношениями, как ${\textstyle \sinh iz=i\sin z}$ между синусом и гиперболическим синусом :

${\begin{aligned}\operatorname {gd} iz&=i\operatorname {gd} ^{-1}z,\\[5mu]\operatorname {gd} ^{-1}iz&=i\operatorname {gd} z.\end{aligned}}$

Обе функции нечетные и коммутируют с комплексным сопряжением . То есть отражение через действительную или мнимую ось в области приводит к такому же отражению в кодомене:

${\begin{aligned}\operatorname {gd} (-z)&=-\operatorname {gd} z,&\quad \operatorname {gd} {\bar {z}}&={\overline {\operatorname {gd} z}},&\quad \operatorname {gd} (-{\bar {z}})&=-{\overline {\operatorname {gd} z}},\\[5mu]\operatorname {gd} ^{-1}(-z)&=-\operatorname {gd} ^{-1}z,&\quad \operatorname {gd} ^{-1}{\bar {z}}&={\overline {\operatorname {gd} ^{-1}z}},&\quad \operatorname {gd} ^{-1}(-{\bar {z}})&=-{\overline {\operatorname {gd} ^{-1}z}}.\end{aligned}}$

Функции периодические , с периодами ${\textstyle 2\pi i}$ и ${\textstyle 2\pi }$:

${\begin{aligned}\operatorname {gd} (z+2\pi i)&=\operatorname {gd} z,\\[5mu]\operatorname {gd} ^{-1}(z+2\pi )&=\operatorname {gd} ^{-1}z.\end{aligned}}$

Перевод в области ${\textstyle \operatorname {gd} }$ к ${\textstyle \pm \pi i}$ приводит к повороту на пол-оборота и трансляции в кодомене одним из ${\textstyle \pm \pi ,}$ и наоборот для ${\textstyle \operatorname {gd} ^{-1}\colon }$

${\begin{aligned}\operatorname {gd} ({\pm \pi i}+z)&={\begin{cases}\pi -\operatorname {gd} z\quad &{\mbox{if }}\ \ \operatorname {Re} z\geq 0,\\[5mu]-\pi -\operatorname {gd} z\quad &{\mbox{if }}\ \ \operatorname {Re} z<0,\end{cases}}\\[15mu]\operatorname {gd} ^{-1}({\pm \pi }+z)&={\begin{cases}\pi i-\operatorname {gd} ^{-1}z\quad &{\mbox{if }}\ \ \operatorname {Im} z\geq 0,\\[3mu]-\pi i-\operatorname {gd} ^{-1}z\quad &{\mbox{if }}\ \ \operatorname {Im} z<0.\end{cases}}\end{aligned}}$

Отражение в области ${\textstyle \operatorname {gd} }$ через любую из линий ${\textstyle x\pm {\tfrac {1}{2}}\pi i}$ приводит к отражению в кодомене через одну из строк ${\textstyle \pm {\tfrac {1}{2}}\pi +yi,}$ и наоборот для ${\textstyle \operatorname {gd} ^{-1}\colon }$

${\begin{aligned}\operatorname {gd} ({\pm \pi i}+{\bar {z}})&={\begin{cases}\pi -{\overline {\operatorname {gd} z}}\quad &{\mbox{if }}\ \ \operatorname {Re} z\geq 0,\\[5mu]-\pi -{\overline {\operatorname {gd} z}}\quad &{\mbox{if }}\ \ \operatorname {Re} z<0,\end{cases}}\\[15mu]\operatorname {gd} ^{-1}({\pm \pi }-{\bar {z}})&={\begin{cases}\pi i+{\overline {\operatorname {gd} ^{-1}z}}\quad &{\mbox{if }}\ \ \operatorname {Im} z\geq 0,\\[3mu]-\pi i+{\overline {\operatorname {gd} ^{-1}z}}\quad &{\mbox{if }}\ \ \operatorname {Im} z<0.\end{cases}}\end{aligned}}$

Это связано с идентичностью

$\tanh {\tfrac {1}{2}}({\pi i}\pm z)=\tan {\tfrac {1}{2}}({\pi }\mp \operatorname {gd} z).$

Конкретные значения

Несколько конкретных значений (где ${\textstyle \infty }$ указывает на предел на одном конце бесконечной полосы):

${\begin{aligned}\operatorname {gd} (0)&=0,&\quad {\operatorname {gd} }{\bigl (}{\pm {\log }{\bigl (}2+{\sqrt {3}}{\bigr )}}{\bigr )}&=\pm {\tfrac {1}{3}}\pi ,\\[5mu]\operatorname {gd} (\pi i)&=\pi ,&\quad {\operatorname {gd} }{\bigl (}{\pm {\tfrac {1}{3}}}\pi i{\bigr )}&=\pm {\log }{\bigl (}2+{\sqrt {3}}{\bigr )}i,\\[5mu]\operatorname {gd} ({\pm \infty })&=\pm {\tfrac {1}{2}}\pi ,&\quad {\operatorname {gd} }{\bigl (}{\pm {\log }{\bigl (}1+{\sqrt {2}}{\bigr )}}{\bigr )}&=\pm {\tfrac {1}{4}}\pi ,\\[5mu]{\operatorname {gd} }{\bigl (}{\pm {\tfrac {1}{2}}}\pi i{\bigr )}&=\pm \infty i,&\quad {\operatorname {gd} }{\bigl (}{\pm {\tfrac {1}{4}}}\pi i{\bigr )}&=\pm {\log }{\bigl (}1+{\sqrt {2}}{\bigr )}i,\\[5mu]&&{\operatorname {gd} }{\bigl (}{\log }{\bigl (}1+{\sqrt {2}}{\bigr )}\pm {\tfrac {1}{2}}\pi i{\bigr )}&={\tfrac {1}{2}}\pi \pm {\log }{\bigl (}1+{\sqrt {2}}{\bigr )}i,\\[5mu]&&{\operatorname {gd} }{\bigl (}{-\log }{\bigl (}1+{\sqrt {2}}{\bigr )}\pm {\tfrac {1}{2}}\pi i{\bigr )}&=-{\tfrac {1}{2}}\pi \pm {\log }{\bigl (}1+{\sqrt {2}}{\bigr )}i.\end{aligned}}$

Производные

Поскольку функции Гудермана и обратные функции Гудермана можно определить как первообразные функций гиперболического секанса и кругового секанса соответственно, их производными являются эти секущие функции:

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {gd} z&=\operatorname {sech} z,\\[10mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {gd} ^{-1}z&=\sec z.\end{aligned}}$

Идентификаторы добавления аргументов

Комбинируя гиперболические и циклические тождества сложения аргументов,

${\begin{aligned}\tanh(z+w)&={\frac {\tanh z+\tanh w}{1+\tanh z\,\tanh w}},\\[10mu]\tan(z+w)&={\frac {\tan z+\tan w}{1-\tan z\,\tan w}},\end{aligned}}$

с кругово-гиперболическим тождеством ,

$\tan {\tfrac {1}{2}}(\operatorname {gd} z)=\tanh {\tfrac {1}{2}}z,$

мы имеем тождества Гудермана-сложения аргументов:

${\begin{aligned}\operatorname {gd} (z+w)&=2\arctan {\frac {\tan {\tfrac {1}{2}}(\operatorname {gd} z)+\tan {\tfrac {1}{2}}(\operatorname {gd} w)}{1+\tan {\tfrac {1}{2}}(\operatorname {gd} z)\,\tan {\tfrac {1}{2}}(\operatorname {gd} w)}},\\[12mu]\operatorname {gd} ^{-1}(z+w)&=2\operatorname {artanh} {\frac {\tanh {\tfrac {1}{2}}(\operatorname {gd} ^{-1}z)+\tanh {\tfrac {1}{2}}(\operatorname {gd} ^{-1}w)}{1-\tanh {\tfrac {1}{2}}(\operatorname {gd} ^{-1}z)\,\tanh {\tfrac {1}{2}}(\operatorname {gd} ^{-1}w)}}.\end{aligned}}$

Дальнейшие тождества сложения аргументов можно записать в терминах других циклических функций: но они требуют большей тщательности при выборе ветвей в обратных функциях. Примечательно,

${\begin{aligned}\operatorname {gd} (z+w)&=u+v,\quad {\text{where}}\ \tan u={\frac {\sinh z}{\cosh w}},\ \tan v={\frac {\sinh w}{\cosh z}},\\[10mu]\operatorname {gd} ^{-1}(z+w)&=u+v,\quad {\text{where}}\ \tanh u={\frac {\sin z}{\cos w}},\ \tanh v={\frac {\sin w}{\cos z}},\end{aligned}}$

который можно использовать для получения покомпонентного расчета для комплексного и обратного Гудерманниана.

В конкретном случае ${\textstyle z=w,}$ тождества с двойными аргументами

${\begin{aligned}\operatorname {gd} (2z)&=2\arctan(\sin(\operatorname {gd} z)),\\[5mu]\operatorname {gd} ^{-1}(2z)&=2\operatorname {artanh} (\sinh(\operatorname {gd} ^{-1}z)).\end{aligned}}$

Серия Тейлора

Ряд Тейлора около нуля, справедлив для комплексных значений ${\textstyle z}$ с ${\textstyle |z|<{\tfrac {1}{2}}\pi ,}$ являются

${\begin{aligned}\operatorname {gd} z&=\sum _{k=0}^{\infty }{\frac {E_{k}}{(k+1)!}}z^{k+1}=z-{\frac {1}{6}}z^{3}+{\frac {1}{24}}z^{5}-{\frac {61}{5040}}z^{7}+{\frac {277}{72576}}z^{9}-\dots ,\\[10mu]\operatorname {gd} ^{-1}z&=\sum _{k=0}^{\infty }{\frac {|E_{k}|}{(k+1)!}}z^{k+1}=z+{\frac {1}{6}}z^{3}+{\frac {1}{24}}z^{5}+{\frac {61}{5040}}z^{7}+{\frac {277}{72576}}z^{9}+\dots ,\end{aligned}}$

где цифры ${\textstyle E_{k}}$ — секущие числа Эйлера , 1, 0, -1, 0, 5, 0, -61, 0, 1385... (последовательности A122045 , A000364 и A028296 в OEIS ). Эти ряды были впервые вычислены Джеймсом Грегори в 1671 году.

Поскольку функции Гудермана и обратные функции Гудермана являются интегралами от гиперболического секущего и секущих функций, числители ${\textstyle E_{k}}$ и ${\textstyle |E_{k}|}$ такие же, как числители ряда Тейлора для sech и sec соответственно, но сдвинуты на одну позицию.

Приведенные беззнаковые числители — 1, 1, 1, 61, 277,…, а приведенные знаменатели — 1, 6, 24, 5040, 72576,… (последовательности A091912 и A136606 в OEIS ).

История

Для более широкого освещения этой темы см. Проекцию Меркатора § История и Интеграл от секущей функции .

Функция и ее обратная относятся к проекции Меркатора . Вертикальная координата в проекции Меркатора называется изометрической широтой и часто обозначается ${\textstyle \psi .}$ По широте ${\textstyle \phi }$ на сфере (выраженной в радианах ) изометрическую широту можно записать

$\psi =\operatorname {gd} ^{-1}\phi =\int _{0}^{\phi }\sec t\,\mathrm {d} t.$

Обратное от изометрической широты к сферической широте: ${\textstyle \phi =\operatorname {gd} \psi .}$ (Примечание: на эллипсоиде вращения связь между геодезической широтой и изометрической широтой несколько сложнее.)

Герард Меркатор составил свою знаменитую карту в 1569 году, но точный метод построения не был раскрыт. В 1599 году Эдвард Райт описал метод численного построения проекции Меркатора по тригонометрическим таблицам, но не вывел закрытой формулы. Закрытая формула была опубликована в 1668 году Джеймсом Грегори .

Функция Гудермана как таковая была введена Иоганном Генрихом Ламбертом в 1760-х годах одновременно с гиперболическими функциями . Он назвал его «трансцендентным углом», и он носил разные названия до 1862 года, когда Артур Кэли предложил дать ему нынешнее название как дань уважения работам Кристофа Гудермана 1830-х годов по теории специальных функций. Гудерман опубликовал в журнале Crelle's Journal статьи , которые позже были собраны в книгу. который излагал ${\textstyle \sinh }$ и ${\textstyle \cosh }$ широкой аудитории (хотя и представлены символами ${\textstyle {\mathfrak {Sin}}}$ и ${\textstyle {\mathfrak {Cos}}}$).

Обозначения ${\textstyle \operatorname {gd} }$ был представлен Кэли, который начал с звонка ${\textstyle \phi =\operatorname {gd} u}$ Якоби эллиптическая амплитуда ${\textstyle \operatorname {am} u}$ в вырожденном случае, когда эллиптический модуль равен ${\textstyle m=1,}$ так что ${\textstyle {\sqrt {1+m\sin \!^{2}\,\phi }}}$ сводится к ${\textstyle \cos \phi .}$ Это обратный интеграл от секущей функции . Используя обозначения Кэли,

$u=\int _{0}{\frac {d\phi }{\cos \phi }}={\log \,\tan }{\bigl (}{\tfrac {1}{4}}\pi +{\tfrac {1}{2}}\phi {\bigr )}.$

Затем он выводит «определение трансцендентного»,

$\operatorname {gd} u={{\frac {1}{i}}\log \,\tan }{\bigl (}{\tfrac {1}{4}}\pi +{\tfrac {1}{2}}ui{\bigr )},$

отмечая, что «хотя оно и проявляется в воображаемой форме, [оно] является реальной функцией ${\textstyle u}$".

Гудерманиан и его обратный были использованы для того, чтобы тригонометрические таблицы круговых функций также функционировали как таблицы гиперболических функций. Учитывая гиперболический угол ${\textstyle \psi }$, гиперболические функции можно найти, сначала поискав ${\textstyle \phi =\operatorname {gd} \psi }$ в таблице Гудермана, а затем ищем соответствующую круговую функцию ${\textstyle \phi }$или непосредственно найдя ${\textstyle \psi }$ во вспомогательном $\operatorname {gd} ^{-1}$ столбец тригонометрической таблицы.

Обобщение

Функцию Гудермана можно рассматривать как отображение точек одной ветви гиперболы в точки полукруга. Точки на одном листе n -мерного гиперболоида из двух листов также могут быть отображены на n -мерную полусферу с помощью стереографической проекции. Модель полушария гиперболического пространства использует такую ​​карту для представления гиперболического пространства.

Приложения

Расстояние в полуплоской модели Пуанкаре гиперболической плоскости от вершины полукруга до другой точки на нем является обратной функцией Гудермана центрального угла.

• Функция угла параллельности в гиперболической геометрии является дополнением гудерманниана: ${\mathit {\Pi }}(\psi )={\tfrac {1}{2}}\pi -\operatorname {gd} \psi .$
• В проекции Меркатора линия постоянной широты параллельна экватору (на проекции) на расстоянии, пропорциональном антигудерманиану широты.
• Функция Гудермана (с комплексным аргументом) может использоваться для определения поперечной проекции Меркатора .
• Функция Гудермана появляется в непериодическом решении перевернутого маятника .
• Функция Гудермана появляется в решении динамического эффекта Казимира в виде движущегося зеркала .
• Если бесконечное количество бесконечно длинных, эквидистантных, параллельных, копланарных, прямых проводов находятся под равными потенциалами с чередующимися знаками, распределение потенциального потока в плоскости поперечного сечения, перпендикулярной проводам, представляет собой комплексную функцию Гудермана.
• Функция Гудермана является сигмовидной функцией и поэтому иногда используется в качестве функции активации в машинном обучении.
• (Масштабированная и сдвинутая) функция Гудермана представляет собой кумулятивную функцию распределения гиперболического секущего распределения .
• Функция, основанная на Гудерманиане, обеспечивает хорошую модель формы рукавов спиральных галактик .

См. также

• Трактрикс
• Цепная связь § Цепная связь равной силы

Ссылки

• Барнетт, Джанет Хейн (2004). «Входите, центр сцены: ранняя драма гиперболических функций» (PDF) . Журнал «Математика» . 77 (1): 15–30. дои : 10.1080/0025570X.2004.11953223 .
• Беккер, Джордж Фердинанд ; Ван Орстранд, Чарльз Эдвин (1909). Гиперболические функции . Смитсоновские математические таблицы. Смитсоновский институт.
• Беккер, Джордж Фердинанд (1912). «Гудерманово дополнение и воображаемая геометрия» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 24 (142): 600–608. дои : 10.1080/14786441008637363 .
• Бейер, Уильям Х., изд. (1987). Справочник CRC по математическим наукам (6-е изд.). ЦРК Пресс. стр. 268–286.
• Кэли, Артур (1862). «О трансцендентном ${\textstyle \operatorname {gd} u={\tfrac {1}{i}}\log \tan {\bigl (}{\tfrac {1}{4}}\pi +{\tfrac {1}{2}}ui{\bigr )}}$« . Философский журнал . 4-я серия. 24 (158): 19–21. doi : 10.1080/14786446208643307 .
• Хорошо, Майкл Р.Р.; Андерсон, Пол Р.; Эванс, Чарльз Р. (2013). «Временная зависимость рождения частиц из ускоряющихся зеркал». Физический обзор D . 88 (2): 025023. arXiv : 1303.6756 . дои : 10.1103/PhysRevD.88.025023 .
• Готшалк, Уолтер (2003). «Хорошие вещи о Гудермане» (PDF) . Гештальты Готшалка .
• Гудерманн, Кристоф (1833). круго-гиперболических функций ( Теория потенциала или на немецком языке). Г. Реймер.
• Дженнингс, Джордж; Ни, Дэвид; Понг, Вай Ян; Райану, Сербан (2022). «Интеграл секущих и стереографических проекций конических сечений». arXiv : 2204.11187 [ math.HO ].
• Калиг, Питер; Райх, Людвиг (2013). Вклад в теорию уравнения Лежандра-Гудермана (PDF) (Технический отчет). Математическая библиотека Университета Карла Франценса в Граце.
• Карни, Чарльз ФФ (2011). «Поперечный Меркатор с точностью до нескольких нанометров» . Журнал геодезии . 85 (8): 475–485. arXiv : 1002.1417 . дои : 10.1007/s00190-011-0445-3 .
• Кеннелли, Артур Э. (1928). «Комплексные углы Гудермана» . Труды Национальной академии наук . 14 (11): 839–844. дои : 10.1073/pnas.14.11.839 . ПМЦ   1085762 .
• Кеннелли, Артур Э. (1929). «Гудерманнианы и ламбертианцы с их соответствующими теоремами сложения» . Труды Американского философского общества . 68 (3): 175–184.
• Ламберт, Иоганн Генрих (1761). «Воспоминания о некоторых замечательных свойствах круговых и логарифмических трансцендентных величин» . История Королевской академии наук и изящной словесности (на французском языке). 17 . Берлин (опубликовано в 1768 г.): 265–322.
• Ли, Лоуренс Патрик (1976). Конформные проекции на основе эллиптических функций . Картографическая монография. Том. 16. Издательство Университета Торонто.
• Лежандр, Адриен-Мари (1817). Упражнения по интегральному исчислению [ Упражнения по интегральному исчислению ] (на французском языке). Полет. 2. Курьер.
• Маерник, В. (1986). «Представление релятивистских величин тригонометрическими функциями» . Американский журнал физики . 54 (6): 536–538. дои : 10.1119/1.14557 .
• МакМахон, Джеймс (1906). Гиперболические функции . Уайли. [Впервые опубликовано как МакМахон (1896 г.). «IV. Гиперболические функции» . В Мерримане; Вудворд (ред.). Высшая математика . Уайли. стр. 107–168. ]
• Массон, Пол (2021). «Комплексный Гудерманиан» . Аналитическая физика .
• Осборн, Питер (2013). «Проекции Меркатора» (PDF) .
• Питерс, JMH (1984). «Гудерманиан». Математический вестник . 68 (445): 192–196. дои : 10.2307/3616342 . JSTOR   3616342 .
• Рейнольдс, Уильям Ф. (1993). «Гиперболическая геометрия на гиперболоиде» (PDF) . Американский математический ежемесячник . 100 (5): 442–455. дои : 10.1080/00029890.1993.11990430 . Архивировано из оригинала (PDF) 28 мая 2016 г.
• Рики, В. Фредерик; Тучинский, Филип М. (1980). «Применение географии к математике: история интеграла секанса» (PDF) . Журнал «Математика» . 53 (3): 162–166. дои : 10.1080/0025570X.1980.11976846 .
• Рингермахер, Гарри И.; Мид, Лоуренс Р. (2009). «Новая формула, описывающая каркасную структуру спиральных галактик» . Ежемесячные уведомления Королевского астрономического общества . 397 (1): 164–171. arXiv : 0908.0892 . дои : 10.1111/j.1365-2966.2009.14950.x .
• Робертсон, Джон С. (1997). «Гудерман и простой маятник». Математический журнал колледжа . 28 (4): 271–276. дои : 10.2307/2687148 . JSTOR   2687148 .
• Ромакина, Людмила Н. (2018). «Обратный Гудерманниан в гиперболической геометрии» . Интегральные преобразования и специальные функции . 29 (5): 384–401. дои : 10.1080/10652469.2018.1441296 .
• Рой, Ранджан; Олвер, Фрэнк У.Дж. (2010), «4. Элементарные функции» , в книге Олвер, Фрэнк У.Дж .; и др. (ред.), Справочник NIST по математическим функциям , издательство Кембриджского университета, ISBN  978-0-521-19225-5 , МР   2723248 .
• Сала, Кеннет Л. (1989). «Преобразования амплитудной функции Якобиана и ее расчет через среднее арифметико-геометрическое» (PDF) . SIAM Journal по математическому анализу . 20 (6): 1514–1528. дои : 10.1137/0520100 .

Внешние ссылки

• Пенн, Майкл (2020) «Функция Гудермана!» на YouTube.