Геодезия

«Геодезический» перенаправляется сюда. О геометрическом понятии, также используемом в Общей теории относительности , см. Геодезика .

Современный прибор для геодезических измерений с использованием спутников.

Геодезия или геодезия Это наука об измерении и представлении геометрии , гравитации и пространственной ориентации Земли пространстве в изменяющемся во времени трехмерном . Ее называют планетарной геодезией при изучении других астрономических тел , например планет или околопланетных систем . Геодезия – это наука о Земле , а также дисциплина прикладной математики . и многие считают, что изучение формы и гравитации Земли занимает центральное место в науке.

Геодинамические явления, включая земной коры движение , приливы и движение полюсов , можно изучать путем разработки глобальных и национальных сетей управления , применения космической геодезии и наземных геодезических методов, а также опираясь на данные и системы координат . Названия геодезических должностей включают геодезиста и геодезиста .

История

Основная статья: История геодезии

Геодезия зародилась еще в донаучную древность , поэтому само слово геодезия происходит от древнегреческого слова γεωδαισία или geodaisia ​​(буквально «разделение Земли»).

Ранние представления о форме Земли считали Землю плоской , а небо — физическим куполом, охватывающим ее. Два первых аргумента в пользу сферической Земли заключались в том, что лунные затмения кажутся наблюдателю круглыми тенями и что Полярная звезда кажется все ниже и ниже в небе путешественнику, направляющемуся на юг.

Определение

На английском языке геодезия относится к науке об измерении и представлении геопространственной информации , а геоматика включает в себя практическое применение геодезии в местных и региональных масштабах, включая геодезию .

В немецком языке геодезия может относиться либо к высшей геодезии ( höhere Geodäsie или Erdmessung , буквально «геомензура») — связанной с измерением Земли в глобальном масштабе, либо к инженерной геодезии ( Ingenieurgeodäsie ), которая включает в себя съемку — измерение частей или регионов Земли.

Долгое время геодезия была наукой об измерении и понимании геометрической формы Земли, ориентации в пространстве и гравитационного поля; однако геодезическая наука и операции применяются и к другим астрономическим телам нашей Солнечной системы .

В значительной степени форма Земли является результатом вращения , которое вызывает ее экваториальную выпуклость , и конкуренции геологических процессов, таких как столкновение плит , а также вулканизма , которому сопротивляется гравитационное поле Земли. Это относится к твердой поверхности, жидкой поверхности ( динамическая топография морской поверхности ) и атмосфере Земли . По этой причине изучение гравитационного поля Земли называется физической геодезией .

Геоид и опорный эллипсоид

Основные статьи: Геоид и опорный эллипсоид

Геоид , приближение формы Земли ; показано здесь с вертикальным преувеличением (коэффициент вертикального масштабирования 10 000).

Эллипсоид — математическое представление Земли . При картографировании в геодезических координатах широтный круг образует усеченный конус.

Экваториальный ( а ), полярный ( б ) и средний радиусы Земли, определенные во Всемирной геодезической системе 1984 года.

Геоид , по сути, представляет собой фигуру Земли, абстрагированную от ее топографических особенностей. Это идеализированная равновесная поверхность морской воды , средняя поверхность уровня моря при отсутствии течений и изменений давления воздуха , продолжающаяся под континентальными массами. В отличие от опорного эллипсоида , геоид нерегулярен и слишком сложен, чтобы служить вычислительной поверхностью для решения геометрических задач, таких как позиционирование точки. Геометрическое расстояние между геоидом и опорным эллипсоидом называется геоидальной волнистостью и варьируется в глобальном масштабе в пределах ± 110 м в зависимости от эллипсоида GRS 80.

Отсчетный эллипсоид, обычно выбираемый того же размера (объема), что и геоид, описывается его большой полуосью (экваториальным радиусом) a и уплощением f . Величина f = a − b / a , где b — малая полуось (полярный радиус), является чисто геометрическим. Механическая эллиптичность Земли (динамическое уплощение, символ J ₂ ) может быть определена с высокой точностью путем наблюдения за возмущениями спутниковой орбиты . Ее связь с геометрическим уплощением косвенная и зависит от распределения внутренней плотности или, проще говоря, степени центральной концентрации массы.

Геодезическая справочная система 1980 года ( GRS 80 ), принятая на XVII Генеральной ассамблее Международного союза геодезии и геофизики ( IUGG ), установила большую полуось длиной 6 378 137 м и уплощение 1: 298,257. GRS 80 по существу представляет собой основу для геодезического позиционирования с помощью Глобальной системы позиционирования (GPS) и, таким образом, также широко используется за пределами геодезического сообщества. Многочисленные системы, используемые для картографирования и составления графиков, устаревают, поскольку страны все чаще переходят к глобальным геоцентрическим системам отсчета, использующим опорный эллипсоид GRS 80.

Геоид — это «реализуемая» поверхность, то есть ее можно последовательно определить на Земле с помощью подходящих простых измерений с помощью физических объектов, таких как маремер . Таким образом, геоид можно считать физической («реальной») поверхностью. Однако эталонный эллипсоид имеет множество возможных реализаций и его нелегко реализовать, поэтому он представляет собой абстрактную поверхность. Третья основная поверхность геодезического интереса — топографическая поверхность Земли — также реализуема.

Системы координат в космосе

Основная статья: Геодезическая система

Дополнительная информация: Мировая геодезическая система.

Сдвиг датума между NAD27 и NAD83 , в метрах

Расположение точек в 3D-пространстве удобнее всего описывать тремя или прямоугольными координатами X , Y и Z. декартовыми С момента появления спутникового позиционирования такие системы координат обычно являются геоцентрическими , при этом ось Z совпадает с осью вращения Земли (обычной или мгновенной).

До эры спутниковой геодезии системы координат, связанные с геодезическими данными, пытались быть геоцентрическими , но с началом координат, отличающимся от геоцентра на сотни метров из-за региональных отклонений в направлении отвеса (вертикали). Эти региональные геодезические датумы, такие как ED 50 (Европейский датум 1950 г.) или NAD 27 (Североамериканский датум 1927 г.), имеют связанные с ними эллипсоиды, которые регионально «наилучшим образом соответствуют» геоидам в пределах их областей действия, сводя к минимуму отклонения вертикально над этими областями.

Только потому, что спутники GPS вращаются вокруг геоцентра, эта точка естественным образом становится началом системы координат, определенной спутниковыми геодезическими средствами, поскольку сами положения спутников в пространстве вычисляются в такой системе.

Геоцентрические системы координат, используемые в геодезии, естественным образом можно разделить на два класса:

1. Инерциальные или, что то же самое , системы отсчета, в которых оси координат сохраняют свою ориентацию относительно неподвижных звезд относительно осей вращения идеальных гироскопов ; ось X указывает на точку весеннего равноденствия.
2. Вращающиеся в одном направлении системы отсчета (также ECEF или «Земля-центрированная, Земля-фиксированная»), в которых оси «прикреплены» к твердому телу Земли. Ось X лежит в Гринвичской обсерватории плоскости меридиана .

Преобразование координат между этими двумя системами с хорошим приближением описывается (кажущимся) звездным временем , которое объясняет изменения осевого вращения Земли ( вариации длины дня ). Более точное описание также объясняет движение полюсов как явление, тщательно отслеживаемое геодезистами.

Системы координат на плоскости

Основная статья: Горизонтальное положение

2D-сетка для эллиптических координат

Мюнхенский . архив с литографическими пластинами карт Баварии

В геодезических приложениях, таких как съемка и картографирование , используются два основных типа систем координат на плоскости:

1. Плоскополярный , с точками в плоскости, определяемыми их расстоянием s от указанной точки вдоль луча, имеющего направление α от базовой линии или оси;
2. Прямоугольный , точки которого определяются расстояниями от двух взаимно перпендикулярных осей x и y . Вопреки математическому соглашению, в геодезической практике ось X указывает на север , а ось Y — на восток .

Можно интуитивно использовать прямоугольные координаты на плоскости для определения своего текущего местоположения, и в этом случае ось X будет указывать на местный север. Более формально, такие координаты могут быть получены из трехмерных координат с использованием картографической проекции . Невозможно нанести на карту изогнутую поверхность Земли на плоскую поверхность карты без деформации. Наиболее часто выбираемый компромисс — называемый конформной проекцией — сохраняет углы и соотношения длин, так что маленькие круги отображаются как маленькие круги, а маленькие квадраты — как квадраты.

Примером такой проекции является UTM ( Universal Transverse Mercator ). Внутри плоскости карты у нас есть прямоугольные координаты x и y . В этом случае северное направление, используемое для справки, — это север карты , а не местный север. Разница между ними называется меридиональной конвергенцией .

«Перевести» между полярными и прямоугольными координатами на плоскости достаточно легко: пусть, как указано выше, направление и расстояние равны α и s соответственно, тогда мы имеем

${\begin{aligned}x&=s\cos \alpha \\y&=s\sin \alpha \end{aligned}}$

Обратное преобразование задается формулой:

${\begin{aligned}s&={\sqrt {x^{2}+y^{2}}}\\\alpha &=\arctan {\frac {y}{x}}.\end{aligned}}$

Высоты

Дополнительная информация: Вертикальное положение и вертикальная точка отсчета.

Измерение высоты с помощью спутниковой альтиметрии

В геодезии высота точки или местности определяется « над уровнем моря » как неровная, физически определенная поверхность.Используемые системы высот:

1. Ортометрические высоты
2. Динамическая высота
3. Геопотенциальные высоты
4. Нормальная высота

Каждая система имеет свои преимущества и недостатки. Как ортометрическая, так и нормальная высоты выражаются в метрах над уровнем моря, тогда как геопотенциальные числа являются мерами потенциальной энергии (единица измерения: м). ² с ⁻² ), а не метрический. Базовой поверхностью является геоид , эквигеопотенциальная поверхность , аппроксимирующая средний уровень моря, как описано выше. Для нормальных высот эталонной поверхностью является так называемый квазигеоид , который находится на расстоянии нескольких метров от геоида из-за предположения о плотности в его продолжении под континентальными массами.

Эти высоты можно связать с помощью концепции волнистости геоида с эллипсоидными высотами (также известными как геодезические высоты ), представляющими высоту точки над опорным эллипсоидом . Приёмники спутникового позиционирования обычно предоставляют эллипсоидные высоты, если они не оснащены специальным программным обеспечением для преобразования, основанным на модели геоида.

Геодезические данные

Основная статья: Преобразование датума

Поскольку координаты и высоты геодезических точек всегда получаются внутри системы, которая сама была построена на основе реальных наблюдений, геодезисты ввели концепцию «геодезической базы данных» (множественное число датумов ): физическая (реальная) реализация координаты. система, используемая для описания местоположения точек. Эта реализация следует из выбора (следовательно, традиционных) значений координат для одной или нескольких исходных точек. В случае данных о высоте достаточно выбрать одну точку отсчета — эталонный ориентир, обычно это маремер на берегу. Таким образом, у нас есть вертикальные датумы, такие как NAVD 88 (Североамериканская вертикальная система отсчета 1988 года), NAP ( Normaal Amsterdams Peil ), система координат Кронштадта, система координат Триеста и многие другие.

И в математике, и в геодезии система координат является «системой координат» согласно терминологии ISO , тогда как Международная служба вращения Земли и систем отсчета (IERS) использует для нее термин «система отсчета». Когда координаты реализуются путем выбора исходных точек и фиксации геодезических исходных данных, ISO говорит о «системе отсчета координат», тогда как IERS использует для этого «систему отсчета». Термин ISO для преобразования исходных данных снова означает «преобразование координат».

Позиционирование

См. Также: Геодезическая сеть § Методы измерений.

GPS Спутник Block IIA находится на орбите Земли .

Первоначальное получение сигнала GPS в 2D

Геопозиционирование , или просто позиционирование, — это определение местоположения, определяемого набором геодезических координат, точки на суше, на море или в пространстве внутри системы координат (позиционирование точки) или относительно другой точки (относительное позиционирование). ). Положение точки в пространстве вычисляется на основе измерений, связывающих земные или внеземные точки известного местоположения («известные точки») с земными точками неизвестного местоположения («неизвестные точки»). Вычисления могут включать преобразования между астрономическими и земными системами координат или между ними. Известные точки, используемые при позиционировании точек, могут быть спутниками GNSS или точками триангуляции сети более высокого порядка.

Традиционно геодезисты строили иерархию сетей, позволяющую позиционировать точки внутри страны. Высшими в этой иерархии были сети триангуляции, уплотненные в сети траверсов ( многоугольников ), в которые завязываются локальные картографические и геодезические измерения, обычно собираемые с помощью рулетки, угловой призмы и красно-белых шестов.

В настоящее время, за исключением специализированных измерений (например, в подземных работах или в высокоточном машиностроении), обычно используется GPS. Сети более высокого порядка измеряются с помощью статического GPS , используя дифференциальные измерения для определения векторов между наземными точками. Эти векторы затем корректируются традиционным сетевым способом. Глобальный многогранник постоянно действующих GPS-станций под эгидой IERS является основой для определения единой глобальной геоцентрической системы отсчета, которая служит точкой отсчета «нулевого порядка» (глобальной), к которой привязаны национальные измерения.

Кинематическое позиционирование в реальном времени (RTK GPS) часто используется при картографировании . При таком методе измерения неизвестные точки могут быть быстро привязаны к близлежащим известным точкам на Земле.

Одной из целей позиционирования точек является предоставление известных точек для картографических измерений, также известных как (горизонтальный и вертикальный) контроль. В стране могут существовать тысячи таких геодезически определенных точек, которые обычно документируются национальными картографическими агентствами. Геодезисты, занимающиеся недвижимостью и страхованием, будут использовать их для привязки своих местных измерений.

Геодезические задачи

Основная статья: Геодезические на эллипсоиде § Решение прямой и обратной задач

Геодезический контрольный знак

Навигационное устройство, программа Аполлон

В геометрической геодезии существуют две основные проблемы:

Первая ( прямая или прямая ) геодезическая задача.

Учитывая координаты точки, направление ( азимут ) и расстояние до второй точки, определите координаты этой второй точки.

Вторая ( обратная или обратная ) геодезическая задача.

Учитывая координаты двух точек, определите азимут и длину линии (прямой, изогнутой или геодезической ), соединяющей эти точки.

Решения обеих задач плоской геометрии сводятся к простой тригонометрии и справедливы для небольших участков земной поверхности; на сфере решения существенно усложняются, так как, например, в обратной задаче азимуты различаются между двумя конечными точками по дуге соединяющего большого круга .

Общее решение называется геодезической поверхности, а дифференциальные уравнения геодезической для рассматриваемой разрешимы численно. На эллипсоиде вращения геодезические выражаются через эллиптические интегралы, которые обычно оцениваются в виде разложения в ряд — см., например, формулы Винсенти .

Концепции

Осевой наклон (или наклон ), ось вращения, плоскость орбиты , небесный экватор и эклиптика . Земля показана со стороны Солнца ; направление орбиты — против часовой стрелки (влево).

Анимация глобальной гравитационной аномалии над океанами от НАСА GRACE (эксперимент по восстановлению гравитации и климата)

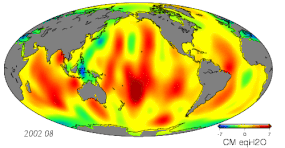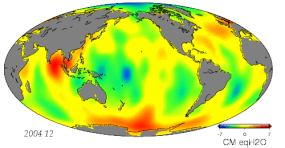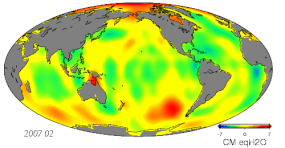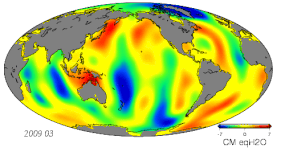
Согласно определению в геодезии (а также астрономии ), некоторые основные понятия наблюдения, такие как углы и координаты, включают (чаще всего с точки зрения местного наблюдателя):

• Отвес или вертикаль : (линия вдоль) направление местной силы тяжести.
• Зенит : пересечение (направление к) направленного вверх вектора гравитации в точке и небесной сферы .
• Надир : антиподальная точка (направление к), в которой направленный вниз вектор гравитации пересекает (скрытую) небесную сферу.
• Небесный горизонт : плоскость, перпендикулярная вектору гравитации в определенной точке.
• Азимут : угол направления внутри плоскости горизонта, обычно отсчитываемый по часовой стрелке с севера (в геодезии и астрономии) или юга (во Франции).
• Высота : угловая высота объекта над горизонтом; альтернативно: зенитное расстояние, равное 90 градусам минус угол места.
• Местные топоцентрические координаты : азимут (угол направления в плоскости горизонта), угол места (или зенитный угол), расстояние.
• Северный полюс мира : продолжение мгновенной оси вращения Земли ( прецессирующей и нутирующей ) простирается на север и пересекает небесную сферу. (Аналогично и для южного полюса мира.)
• Небесный экватор : (мгновенное) пересечение экваториальной плоскости Земли с небесной сферой.
• Меридианная плоскость : любая плоскость, перпендикулярная небесному экватору и содержащая небесные полюса.
• Местный меридиан : плоскость, содержащая направление на зенит и полюс мира.

Измерения

Дополнительная информация: Спутниковая геодезия , Геодезическая астрономия , Геодезия , Гравиметрия и Нивелирование.

Вариации гравитационного поля Луны , данные НАСА.

Приборы для измерения силы тяжести: маятник (слева) и абсолютный гравиметр (справа)

Относительный гравиметр

Базовая поверхность (уровень), используемая для определения перепадов высот и систем отсчета высот, известна как средний уровень моря . Традиционный ватерпас непосредственно обеспечивает такую ​​(наиболее полезную для практических целей) высоту над уровнем моря ; более экономичное использование инструментов GPS для определения высоты требует точного знания фигуры геоида , поскольку GPS дает только высоты выше опорного эллипсоида GRS80 . По мере совершенствования определения геоида можно ожидать, что использование GPS для определения высоты также будет увеличиваться.

Теодолит — это инструмент , используемый для измерения горизонтальных и вертикальных (относительно местной вертикали) углов к целевым точкам. Кроме того, тахиметр определяет электронным или электрооптическим способом расстояние до цели и работает в высокой степени автоматизированно или даже роботизировано. Широко используется с этой же целью метод свободного положения станции.

Обычно для локальных детальных съемок используются тахиметры, хотя старомодный прямоугольный метод с использованием угловой призмы и стальной ленты по-прежнему является недорогой альтернативой. Как уже упоминалось, существуют быстрые и относительно точные методы кинематики GPS в реальном времени (RTK). Собранные данные маркируются и записываются в цифровом виде для ввода в базы данных Географической информационной системы (ГИС).

Геодезические приемники GNSS (чаще всего GPS ) непосредственно создают трехмерные координаты в геоцентрической системе координат. Одним из таких кадров является WGS84 , а также кадры Международной службы вращения Земли и систем отсчета ( IERS ). Приёмники ГНСС почти полностью заменили наземные инструменты для крупномасштабных исследований базовой сети.

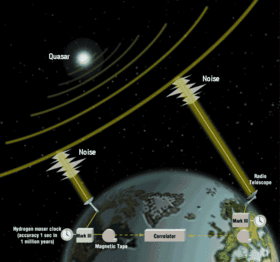
Для мониторинга неравномерностей вращения Земли и тектонических движений плит, а также для общепланетных геодезических исследований используются методы интерферометрии со сверхдлинной базой (РСДБ) для измерения расстояний до квазаров , лунной лазерной локации (ЛЛР) для измерения расстояний до призм на Луне и спутниковых технологий. лазерные локаторы (SLR) для измерения расстояний до призм на искусственных спутниках используются .

Гравитацию измеряют с помощью гравиметров , которых существует два вида. Во-первых, это абсолютные гравиметры , основанные на измерении ускорения свободного падения (например, отражающей призмы в вакуумной трубке ). Они используются для установления вертикального геопространственного контроля или в полевых условиях. Во-вторых, относительные гравиметры являются пружинными и более распространенными. Их используют при гравиметрических съемках на больших территориях — для установления фигуры геоида на этих территориях. Самые точные относительные гравиметры называются сверхпроводящими гравиметрами , которые чувствительны к одной тысячной одной миллиардной гравитации земной поверхности. Двадцать с лишним сверхпроводящих гравиметров используются во всем мире для изучения приливов , вращения , внутренних, океанических и атмосферных нагрузок Земли, а также для проверки ньютоновской постоянной гравитации .

В будущем гравитацию и высоту можно будет измерить с помощью специальной релятивистской концепции замедления времени , измеряемой оптическими часами .

Единицы и меры на эллипсоиде

Дополнительная информация: Геодезические координаты.

Определение широты (φ) и долготы (λ) на эллипсоиде вращения (или сфероиде). Шаг сетки составляет 10 градусов. Широта определяется как угол между нормалью к эллипсоиду и плоскостью экватора.

Географическая широта и долгота выражаются в градусах, угловых минутах и ​​угловых секундах. Это углы , а не метрика.меры и описать направление локальной нормали к опорному эллипсоиду вращения. Это направление примерно совпадает с направлением отвеса, т. е. местной силы тяжести, которая также является нормалью к поверхности геоида. По этой причине определение астрономического положения – измерение направления отвеса астрономическими средствами – работает достаточно хорошо, когда используется также эллипсоидальная модель фигуры Земли.

Одна географическая миля, определяемая как одна угловая минута на экваторе, равна 1855,32571922 м. Одна морская миля — это одна минута астрономической широты. Радиус кривизны эллипсоида меняется в зависимости от широты: он самый длинный на полюсе и самый короткий на экваторе, как и морская миля.

Первоначально метр частей определялся как 10-миллионная часть длины от экватора до Северного полюса вдоль меридиана, проходящего через Париж (цель не была полностью достигнута на практике, поскольку в текущих определениях она отклоняется на 200 миллион на ). Эта ситуация означает, что один километр примерно равен (1/40 000) * 360 * 60 меридиональных угловых минут, или 0,54 морской мили. (Это не совсем так, поскольку эти две единицы были определены на разных основах, поэтому международная морская миля составляет ровно 1852 м, что соответствует округлению 1000/0,54 м до четырех цифр).

Временные изменения

См. Также: Геоид § Временное изменение

Глобальное тектоническое движение плит с использованием GPS

Как работает интерферометрия со сверхдлинной базой (РСДБ)

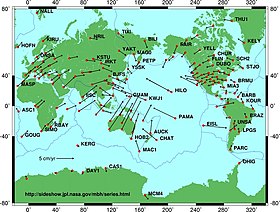
В геодезии используются различные методы для изучения изменяющихся во времени поверхностей, тел, физических полей и динамических систем. Точки на поверхности Земли меняют свое расположение благодаря множеству механизмов:

• Движение континентальных плит, тектоника плит
• Эпизодические движения тектонического происхождения, особенно вблизи линий разломов.
• Периодические эффекты, вызванные приливами и приливными нагрузками
• Послеледниковое поднятие суши из-за изостатической корректировки
• Изменения массы из-за гидрологических изменений, включая атмосферу, криосферу, гидрологию суши и океанов.
• Субсуточное движение полюсов
• Изменчивость продолжительности дня
• Вариации центра масс (геоцентра) Земли
• Антропогенные движения, такие как строительство резервуаров или добыча нефти или воды.

Продолжительность: 2 минуты 8 секунд. 2:08

Менеджер проекта НАСА рассказывает о своей работе в рамках проекта «Космическая геодезия» , включая обзор его четырех фундаментальных методов: GPS, VLBI , LLR / SLR и DORIS .

Геодинамика — дисциплина, изучающая деформации и движения земной коры и ее твердости в целом. Часто в приведенное выше определение включается изучение неравномерного вращения Земли. Геодинамические исследования требуют наземных систем отсчета. реализуемые станциями, принадлежащими Глобальной системе геодезических наблюдений (GGOS ).

К методам изучения геодинамических явлений в глобальных масштабах относятся:

• Спутниковое позиционирование с помощью GPS , ГЛОНАСС , Galileo и BeiDou.
• Интерферометрия со сверхдлинной базой (РСДБ)
• Спутниковая лазерная локация (SLR) и лунная лазерная локация (ЛЛР)
• ДОРИС
• Региональное и локальное точное нивелирование
• Точные тахиметры
• Мониторинг изменения силы тяжести с использованием наземной, воздушной, корабельной и космической гравиметрии.
• Спутниковая альтиметрия на основе микроволновых и лазерных наблюдений для изучения поверхности океана, повышения уровня моря и мониторинга ледяного покрова.
• Интерферометрический радар с синтезированной апертурой (InSAR) с использованием спутниковых изображений.

геодезисты

Основная статья: Список геодезистов

См. Также: Известные геодезисты

См. также

Основная статья: Очерк метрологии и измерений § Геодезия

Основная категория: Геодезия

• Наука о системе Земли - Научное исследование сфер Земли и их естественных интегрированных систем.
• Список геодезистов - Известные геодезисты
• Геоматика – дисциплина географических данных. Страницы с краткими описаниями целей перенаправления.
• История геофизики
• Геодинамика - Исследование динамики Земли.
• Планетология - Наука о планетах и ​​планетных системах.

Основы

• Геодезия (книга)
• Концепции и методы в современной географии
• Геодезические на эллипсоиде
• История геодезии
• Физическая геодезия
• Окружность Земли
• Физика
• Геонауки

Государственные учреждения

• Национальное картографическое агентство
• Национальная геодезическая служба США
• Национальное агентство геопространственной разведки
• Обзор боеприпасов
• Береговая и геодезическая служба США
• Геологическая служба США

Международные организации

• Международный союз геодезии и геофизики (IUGG)
• Международная ассоциация геодезии (IAG)
• Международная федерация геодезистов (IFS)
• Международная студенческая геодезическая организация (IGSO)

Другой

• Набор данных геодезических параметров EPSG
• Меридианная дуга
• Геодезия

Дальнейшее чтение

• Ф. Р. Гельмерт, Математические и физические теории высшей геодезии , Часть 1 , ACIC (Сент-Луис, 1964). Это английский перевод книги «Математические и физические теории высшей геодезии» , том 1 (Тойбнер, Лейпциг, 1880 г.).
• Ф. Р. Гельмерт, Математические и физические теории высшей геодезии , Часть 2 , ACIC (Сент-Луис, 1964). Это английский перевод книги «Математические и физические теории высшей геодезии» , том 2 (Тойбнер, Лейпциг, 1884 г.).
• Б. Хофманн-Велленхоф и Х. Мориц, Физическая геодезия , Springer-Verlag Wien, 2005. (Этот текст представляет собой обновленное издание классической книги 1967 года В. А. Хейсканена и Х. Морица).
• В. Каула, Теория спутниковой геодезии: Применение спутников в геодезии , Dover Publications, 2000. (Этот текст представляет собой переиздание классического издания 1966 года).
• Ваничек П. и Э. Я. Кракивский, Геодезия: концепции , стр. 714, Эльзевир, 1986.
• Торге, W (2001), Геодезия (3-е издание), опубликовано де Грюйтером, ISBN   3-11-017072-8 .
• Томас Х. Мейер, Дэниел Р. Роман и Дэвид Б. Зилкоски. «Что на самом деле означает высота ?» (Это серия из четырех статей, опубликованных в журнале Surveying and Land Information Science, SaLIS .)
  • «Часть I: Введение» SaLIS Vol. 64, № 4, страницы 223–233, декабрь 2004 г.
  • «Часть II: Физика и гравитация» SaLIS Vol. 65, № 1, страницы 5–15, март 2005 г.
  • «Часть III: Системы высот» SaLIS Vol. 66, № 2, страницы 149–160, июнь 2006 г.
  • «Часть IV: Определение высоты по GPS» SaLIS Vol. 66, № 3, страницы 165–183, сентябрь 2006 г.

Внешние ссылки

Геодезия в Wikibooks СМИ, связанные с геодезией , на Викискладе?

• Руководство по повышению осведомленности о геодезии, Подкомитет по геодезии, Комитет по геоматике, Международная ассоциация производителей нефти и газа
• «Геодезия» . Британская энциклопедия . Том. 11 (11-е изд.). 1911. стр. 607–615.