Физическая геодезия

Физическая геодезия — изучение физических свойств силы тяжести Земли и ее потенциального поля ( геопотенциала ) с целью их применения в геодезии .

Процедура измерения

Традиционные геодезические инструменты, такие как теодолиты, полагаются на гравитационное поле для ориентации своей вертикальной оси вдоль местного отвеса или местного вертикального направления с помощью спиртового уровня . После этого получаются вертикальные углы ( зенитные углы или, альтернативно, углы места ) относительно этой местной вертикали, и горизонтальные углы в плоскости местного горизонта, перпендикулярной вертикали.

Нивелирные инструменты снова используются для получения разницы геопотенциалов между точками на поверхности Земли. Затем их можно выразить как разницу «высот» путем преобразования в метрические единицы.

Единицы

Гравитация обычно измеряется в м·с. ⁻² ( метров на секунду в квадрате). Это также можно выразить (умножив на гравитационную постоянную G , чтобы изменить единицы измерения) в ньютонах на килограмм притянутой массы.

Потенциал выражается как сила тяжести, умноженная на расстояние, м. ²·с ⁻². Перемещение на один метр в направлении вектора силы тяжести 1 м·с. ⁻² увеличит ваш потенциал на 1 м ²·с ⁻². Опять же, используя G в качестве множителя, единицы измерения можно изменить на джоули на килограмм притянутой массы.

Более удобной единицей измерения является ГПУ, или геопотенциальная единица: она равна 10 м. ²·с ⁻². Это означает, что перемещение на один метр в вертикальном направлении, т. е. в направлении скорости 9,8 м·с. ⁻² окружающая гравитация примерно изменит ваш потенциал на 1 графический процессор. Это снова означает, что разницу геопотенциала точки в GPU с геопотенциалом уровня моря можно использовать как грубую меру высоты «над уровнем моря» в метрах.

Гравитация

Гравитация Земли , обозначаемая $g$ , представляет собой чистое ускорение , которое передается объектам из-за комбинированного эффекта гравитации (из-за распределения массы внутри Земли ) и центробежной силы (из-за вращения Земли ). ^[2]^[3]Это векторная величина, направление которой совпадает с отвесом , а сила или величина задается нормой . $g=\|{\mathit {\mathbf {g} }}\|$ .

В единицах СИ это ускорение выражается в метрах на секунду в квадрате (в символах, м / с ² или м·с ⁻²) или эквивалентно в ньютонах на килограмм (Н/кг или Н·кг ⁻¹). У поверхности Земли ускорение свободного падения с точностью до 2 значащих цифр составляет 9,8 м/с. ² (32 фута/с ²). Это означает, что, если игнорировать влияние сопротивления воздуха , скорость объекта свободно падающего будет увеличиваться примерно на 9,8 метра в секунду (32 фута/с) каждую секунду. Эту величину иногда неофициально называют маленькой $g$ (напротив, гравитационную постоянную $G$ называют большой $G$ ).

Точная сила гравитации Земли варьируется в зависимости от местоположения. Согласованное значение стандартной силы тяжести составляет 9,80665 м/с. ² (32,1740 футов/с ²) по определению. ^[4] Эту величину обозначают по-разному как $g n$ , $ge .$ (хотя иногда это означает нормальную силу тяжести на экваторе, 9,7803267715 м/с) ² (32,087686258 футов/с ²)), ^[5] $g 0$ или просто $g$ (который также используется для локального значения переменной).

Вес вторым объекта на поверхности Земли — это сила, действующая вниз на этот объект, определяемая законом движения Ньютона , или

F = m a

( сила = масса × ускорение ). Гравитационное ускорение способствует общему ускорению силы тяжести, но другие факторы, такие как вращение Земли, также вносят свой вклад и, следовательно, влияют на вес объекта. Гравитация обычно не включает гравитационное притяжение Луны и Солнца, которое учитывается с точки зрения приливных эффектов .

Потенциальные поля

Геопотенциал это потенциал гравитационного Земли поля . – Для удобства его часто определяют как отрицательную величину потенциальной энергии на единицу массы , так что вектор гравитации получается как градиент геопотенциала без отрицания. Помимо реального потенциала (геопотенциала) можно определить также гипотетический нормальный потенциал и их разность — возмущающий потенциал.

геоид

Из-за неравномерности истинного гравитационного поля Земли фигура равновесия морской воды, или геоид , также будет иметь неправильную форму. В некоторых местах, например, к западу от Ирландии , геоид — средний математический уровень моря — выступает на целых 100 м над правильным вращательно-симметричным опорным эллипсоидом GRS80; в других местах, например вблизи Шри-Ланки , он ныряет под эллипсоид почти на такую же величину. Расстояние между геоидом и опорным эллипсоидом называется волнистостью геоида , символ $N$ .

Геоид, или средняя математическая поверхность моря, определяется не только на море, но и под сушей; если бы морской воде было разрешено свободно перемещаться (например, через туннели) под землей, то это была бы равновесная водная поверхность. Технически — эквипотенциальная поверхность истинного геопотенциала, выбранная так, чтобы она совпадала (в среднем) со средним уровнем моря.

Поскольку средний уровень моря физически определяется по мареографическим отметкам на побережьях разных стран и континентов, в результате возникнет ряд слегка несовместимых «окологеоидов» с разницей между ними от нескольких дециметров до более одного метра из-за динамического изменения уровня моря . Топография морской поверхности . Они называются вертикальными датумами или высот базами .

Для каждой точки на Земле местное направление силы тяжести или вертикальное направление , материализованное отвесом , перпендикулярно геоиду (см. астрогеодезическое нивелирование ).

Гравитационные аномалии

Выше мы уже использовали гравитационные аномалии. $\Delta g$ . Они рассчитываются как разница между истинной (наблюдаемой) гравитацией $g=\|{\vec {g}}\|$ и расчетная (нормальная) гравитация $\gamma =\|{\vec {\gamma }}\|=\|\nabla U\|$ . (Это чрезмерное упрощение; на практике место в пространстве, в котором оценивается γ, будет немного отличаться от того, где g измерялось .) Таким образом, мы получаем

\Delta g=g-\gamma .\,

Эти аномалии называются аномалиями в свободном воздухе , и именно их следует использовать в приведенном выше уравнении Стокса.

В геофизике эти аномалии часто дополнительно уменьшают, убирая из них притяжение топографии , которое для плоской горизонтальной пластины ( плиты Буге ) толщины H определяется выражением

a_{B}=2\pi G\rho H,\,

Сокращение Бугера применяется следующим образом:

\Delta g_{B}=\Delta g_{FA}-a_{B},\,

так называемые аномалии Бугера . Здесь, $\Delta g_{FA}$ это наш предыдущий $\Delta g$ , аномалия в свободном воздухе.

В случае, если местность не является плоской пластиной (обычный случай!), мы используем для H значение локальной высоты местности, но применяем дополнительную поправку, называемую коррекцией местности .

См. также

Ссылки

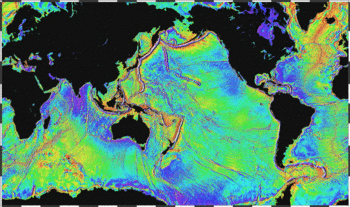
^ НАСА/Лаборатория реактивного движения/Центр космических исследований Техасского университета. «PIA12146: Анимация глобальной гравитации GRACE» . Фотожурнал . Лаборатория реактивного движения НАСА . Проверено 30 декабря 2013 г.
^ Бойнтон, Ричард (2001). « Точное измерение массы » (PDF) . Бумага Саве № 3147 . Арлингтон, Техас: SAWE, Inc. Архивировано из оригинала (PDF) 27 февраля 2007 года . Проверено 22 декабря 2023 г.
^ Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Спрингер. ISBN 978-3-211-33544-4 . § 2.1: «Суммарная сила, действующая на тело, покоящееся на земной поверхности, является равнодействующей силы гравитации и центробежной силы вращения Земли и называется гравитацией».
^ Международное бюро мер и весов (1901 г.). «Положение, касающееся единицы массы и определения веса; условное значение $г н$ ». Отчеты сессий Третьей Генеральной конференции мер и весов (на французском языке). Париж: Готье-Виллар. п. 68. Число, принятое Международной службой мер и весов для значения нормального ускорения силы тяжести, составляет 980,665 см/сек², число, уже санкционированное некоторыми законами. Декларация, касающаяся единицы массы и определения веса; условное значение $g n$ .
^ Мориц, Хельмут (2000). «Геодезическая справочная система 1980 года» . Журнал геодезии . 74 (1): 128–133. дои : 10.1007/s001900050278 . S2CID 195290884 . Проверено 26 июля 2023 г. γe = 9,780 326 7715 м/с² нормальная сила тяжести на экваторе

Дальнейшее чтение

Б. Хофманн-Велленхоф и Х. Мориц, Физическая геодезия, Springer-Verlag Wien, 2005. (Этот текст представляет собой обновленное издание классической книги 1967 года В. А. Хейсканена и Х. Морица).

[1] НАСА/Лаборатория реактивного движения/Центр космических исследований Техасского университета. «PIA12146: Анимация глобальной гравитации GRACE» . Фотожурнал . Лаборатория реактивного движения НАСА . Проверено 30 декабря 2013 г.

[Gravity_of_Earth_Boynton-2] Бойнтон, Ричард (2001). « Точное измерение массы » (PDF) . Бумага Саве № 3147 . Арлингтон, Техас: SAWE, Inc. Архивировано из оригинала (PDF) 27 февраля 2007 года . Проверено 22 декабря 2023 г.

[3] Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Спрингер. ISBN 978-3-211-33544-4 . § 2.1: «Суммарная сила, действующая на тело, покоящееся на земной поверхности, является равнодействующей силы гравитации и центробежной силы вращения Земли и называется гравитацией».

[4] Международное бюро мер и весов (1901 г.). «Положение, касающееся единицы массы и определения веса; условное значение $г н$ ». Отчеты сессий Третьей Генеральной конференции мер и весов (на французском языке). Париж: Готье-Виллар. п. 68. Число, принятое Международной службой мер и весов для значения нормального ускорения силы тяжести, составляет 980,665 см/сек², число, уже санкционированное некоторыми законами. Декларация, касающаяся единицы массы и определения веса; условное значение $g n$ .

[5] Мориц, Хельмут (2000). «Геодезическая справочная система 1980 года» . Журнал геодезии . 74 (1): 128–133. дои : 10.1007/s001900050278 . S2CID 195290884 . Проверено 26 июля 2023 г. γe = 9,780 326 7715 м/с² нормальная сила тяжести на экваторе

[1]

[2]

[3]

[4]

[5]