Гравитация Земли

Гравитация Земли , обозначаемая $g$ , представляет собой чистое ускорение , которое передается объектам из-за комбинированного эффекта гравитации (из-за распределения массы внутри Земли ) и центробежной силы (из-за вращения Земли ). ^[2]^[3] Это векторная величина, направление которой совпадает с отвесом, а сила или величина задается нормой . $g=\|{\mathit {\mathbf {g} }}\|$ .

В единицах СИ это ускорение выражается в метрах на секунду в квадрате (в символах, м / с ² или м·с ⁻²) или эквивалентно в ньютонах на килограмм (Н/кг или Н·кг ⁻¹). У поверхности Земли ускорение свободного падения с точностью до 2 значащих цифр составляет 9,8 м/с. ² (32 фута/с ²). Это означает, что, если игнорировать влияние сопротивления воздуха , скорость объекта свободно падающего будет увеличиваться примерно на 9,8 метра в секунду (32 фута/с) каждую секунду. Эту величину иногда неофициально называют маленькой $g$ (напротив, гравитационную постоянную $G$ называют большой $G$ ).

Точная сила гравитации Земли варьируется в зависимости от местоположения. Согласованное значение стандартной силы тяжести составляет 9,80665 м/с. ² (32,1740 футов/с ²) по определению. ^[4] Эту величину обозначают по-разному как $g n$ , $ge .$ (хотя иногда это означает нормальную силу тяжести на экваторе, 9,7803267715 м/с) ² (32,087686258 футов/с ²)), ^[5] $g 0$ или просто $g$ (который также используется для локального значения переменной).

Вес вторым объекта на поверхности Земли — это сила, действующая вниз на этот объект, определяемая законом движения Ньютона , или $F = m a$ ( сила = масса × ускорение ). Гравитационное ускорение способствует общему гравитационному ускорению, но другие факторы, такие как вращение Земли, также вносят свой вклад и, следовательно, влияют на вес объекта. Гравитация обычно не включает гравитационное притяжение Луны и Солнца, которое учитывается с точки зрения приливных эффектов .

Изменение величины [ править ]

Невращающаяся идеальная сфера с одинаковой плотностью массы или плотность которой меняется исключительно в зависимости от расстояния от центра ( сферическая симметрия ) будет создавать гравитационное поле одинаковой величины во всех точках ее поверхности . Земля вращается и не имеет сферической симметрии; скорее, он немного более плоский на полюсах и выпуклый на экваторе: сплюснутый сфероид . Следовательно, на его поверхности наблюдаются небольшие отклонения в величине силы тяжести.

Гравитация на поверхности Земли меняется примерно на 0,7%, от 9,7639 м/с. ² на горе Невадо-Уаскаран в Перу до 9,8337 м/с. ² на поверхности Северного Ледовитого океана . ^[6] В крупных городах она колеблется в пределах 9,7806 м/с. ²^[7] в Куала-Лумпуре , Мехико и Сингапуре до 9,825 м/с. ² в Осло и Хельсинки .

Обычное значение [ править ]

В 1901 году третья Генеральная конференция по мерам и весам определила стандартное ускорение свободного падения для поверхности Земли: g _n = 9,80665 м/с. ². Он был основан на измерениях в Павильоне Бретей недалеко от Парижа в 1888 году с теоретической поправкой, примененной для преобразования в широту 45 ° на уровне моря. ^[8] Таким образом, это определение не является значением какого-либо конкретного места или тщательно рассчитанным средним значением, а соглашением о значении, которое следует использовать, если лучшее фактическое местное значение неизвестно или не важно. ^[9] Он также используется для определения единиц силы килограмм и силы фунта .

Широта [ править ]

Поверхность Земли вращается, поэтому она не является инерциальной системой отсчета . На широтах ближе к экватору внешняя центробежная сила , создаваемая вращением Земли, больше, чем в полярных широтах. Это в небольшой степени противодействует гравитации Земли – максимум до 0,3% на экваторе – и уменьшает кажущееся ускорение падающих объектов вниз.

Земли Вторая основная причина разницы в гравитации на разных широтах заключается в том, что экваториальная выпуклость (которая сама по себе также вызвана центробежной силой вращения) заставляет объекты на экваторе находиться дальше от центра планеты, чем объекты на полюсах. Сила гравитационного притяжения между двумя массами (куском Земли и взвешиваемым объектом) изменяется обратно пропорционально квадрату расстояния между ними. Распределение массы также различно ниже кого-то на экваторе и ниже кого-то на полюсе. В результате объект на экваторе испытывает более слабое гравитационное притяжение, чем объект на одном из полюсов.

В сочетании экваториальная выпуклость и воздействие поверхностной центробежной силы из-за вращения означают, что сила тяжести на уровне моря увеличивается примерно с 9,780 м/с. ² на экваторе примерно до 9,832 м/с. ² на полюсах, поэтому на полюсах объект будет весить примерно на 0,5% больше, чем на экваторе. ^[2]^[10]

Высота [ править ]

График показывает изменение силы тяжести в зависимости от высоты объекта над поверхностью.

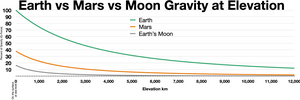
Гравитация уменьшается с высотой по мере подъема над поверхностью Земли, поскольку большая высота означает большее расстояние от центра Земли. При прочих равных условиях увеличение высоты от уровня моря до 9000 метров (30 000 футов) приводит к уменьшению веса примерно на 0,29%. (Дополнительным фактором, влияющим на видимый вес, является уменьшение плотности воздуха на высоте, что снижает плавучесть объекта. ^[11] Это увеличит видимый вес человека на высоте 9000 метров примерно на 0,08%).

Распространено заблуждение, что астронавты на орбите невесомы, потому что они пролетели достаточно высоко, чтобы избежать земной гравитации. Фактически, на высоте 400 километров (250 миль), что соответствует типичной орбите МКС , гравитация по-прежнему почти на 90% сильнее, чем на поверхности Земли. Невесомость на самом деле возникает потому, что объекты на орбите находятся в свободном падении . ^[12]

Эффект подъема грунта зависит от плотности грунта (см. раздел «Коррекция плиты» ). Человек, летящий на высоте 9100 м (30 000 футов) над уровнем моря над горами, будет чувствовать большую гравитацию, чем человек, находящийся на той же высоте, но над морем. Однако человек, стоящий на поверхности Земли, ощущает меньшую гравитацию при большей высоте.

Следующая формула аппроксимирует изменение силы тяжести Земли с высотой:

g_{h}=g_{0}\left({\frac {R_{\mathrm {e} }}{R_{\mathrm {e} }+h}}\right)^{2}

Где

$g h$ — ускорение свободного падения на высоте $h$ над уровнем моря.
$R e$ — средний радиус Земли .
$g 0$ — стандартное гравитационное ускорение .

Формула рассматривает Землю как идеальную сферу с радиально-симметричным распределением массы; более точная математическая трактовка обсуждается ниже.

Глубина [ править ]

Гравитация в разных внутренних слоях Земли (1 = континентальная кора, 2 = океаническая кора, 3 = верхняя мантия, 4 = нижняя мантия, 5+6 = ядро, A = граница кора-мантия)

Распределение радиальной плотности Земли согласно предварительной эталонной модели Земли (PREM). ^[13]

Гравитация Земли согласно предварительной эталонной модели Земли (PREM). ^[13]Для сравнения включены две модели сферически-симметричной Земли. Темно-зеленая прямая линия соответствует постоянной плотности, равной средней плотности Земли. Светло-зеленая изогнутая линия соответствует плотности, которая линейно уменьшается от центра к поверхности. Плотность в центре такая же, как и в ПРЭМ, но поверхностная плотность выбрана так, чтобы масса сферы равнялась массе реальной Земли.

Приблизительное значение силы тяжести на расстоянии $r$ от центра Земли можно получить, предположив, что плотность Земли сферически симметрична. Гравитация зависит только от массы внутри сферы радиуса $r$ . Все вклады извне компенсируются вследствие закона обратных квадратов гравитации. Другим следствием является то, что гравитация такая же, как если бы вся масса была сосредоточена в центре. Таким образом, гравитационное ускорение на этом радиусе равно ^[14]

g(r)=-{\frac {GM(r)}{r^{2}}}.

где $G$ — гравитационная постоянная , а $M (r)$ — общая масса, заключенная в радиусе $r$ . Если бы Земля имела постоянную плотность $ρ$ , масса была бы $M (r) = (4/3) πρr. 3$ и зависимость силы тяжести от глубины будет

g(r)={\frac {4\pi }{3}}G\rho r.

Гравитация $g'$ на глубине $d$ определяется выражением $g' = g (1 - d / R)$ , где $g$ — ускорение силы тяжести на поверхности Земли, $d$ — глубина, а $R$ — радиус Земли . Если бы плотность уменьшалась линейно с увеличением радиуса от плотности $ρ 0$ в центре до $ρ 1$ на поверхности, то $ρ (r) = ρ 0 - (ρ 0 - ρ 1) r / R$ , и зависимость была бы следующей:

g(r)={\frac {4\pi }{3}}G\rho _{0}r-\pi G\left(\rho _{0}-\rho _{1}\right){\frac {r^{2}}{R}}.

Фактическая зависимость плотности и гравитации от глубины, полученная на основе времени сейсмического распространения (см. уравнение Адамса-Вильямсона ), показана на графиках ниже.

и геология Местная топография

Локальные различия в топографии (например, наличие гор), геологии (например, плотность горных пород поблизости) и более глубокой тектонической структуре вызывают локальные и региональные различия в гравитационном поле Земли, известные как гравитационные аномалии . ^[15] Некоторые из этих аномалий могут быть очень обширными, что приводит к повышению уровня моря и нарушению маятниковых синхронизации часов.

Изучение этих аномалий составляет основу гравитационной геофизики . Колебания измеряются высокочувствительными гравиметрами , вычитается влияние топографии и других известных факторов и на основе полученных данных делаются выводы. Такие методы сейчас используются старателями для поиска нефти и месторождений полезных ископаемых . Более плотные породы (часто содержащие минеральные руды ) вызывают более сильные, чем обычно, локальные гравитационные поля на поверхности Земли. Менее плотные осадочные породы вызывают обратное.

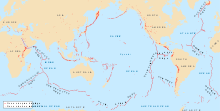
Существует сильная корреляция между картой гравитационного воздействия Земли, составленной НАСА GRACE, с положением недавней вулканической активности, распространением хребтов и вулканами: эти регионы имеют более сильную гравитацию, чем теоретические предсказания.

Другие факторы [ править ]

В воздухе или воде объекты испытывают поддерживающую силу плавучести , которая уменьшает кажущуюся силу гравитации (измеряемую весом объекта). Величина эффекта зависит от плотности воздуха (и, следовательно, давления воздуха) или плотности воды соответственно; см . в разделе «Кажущийся вес» подробности .

Гравитационное воздействие Луны и Солнца ( также являющееся причиной приливов и отливов ) оказывает очень незначительное влияние на кажущуюся силу земного притяжения в зависимости от их взаимного положения; типичные отклонения составляют 2 мкм/с. ² (0,2 мГал ) в течение суток.

Направление [ править ]

Ускорение свободного падения является векторной величиной , имеющей направление помимо величины . На сферически-симметричной Земле гравитация будет направлена прямо к центру сферы. Поскольку фигура Земли немного более плоская, следовательно, возникают значительные отклонения в направлении силы тяжести: по сути, это разница между геодезической широтой и геоцентрической широтой . Меньшие отклонения, называемые вертикальными отклонениями , вызваны локальными аномалиями массы, например, горами.

Сравнительные значения по всему миру

Существуют инструменты для расчета силы гравитации в различных городах мира. ^[16] Влияние широты можно ясно увидеть по гравитации в городах, расположенных в высоких широтах: Анкоридж (9,826 м/с). ²), Хельсинки (9,825 м/с ²), что примерно на 0,5% больше, чем в городах вблизи экватора: Куала-Лумпур (9,776 м/с). ²). Влияние высоты можно увидеть в Мехико (9,776 м/с). ²; высота 2240 метров (7350 футов)), и сравнивая Денвер (9,798 м / с ²; 1616 метров (5302 футов)) с Вашингтоном, округ Колумбия (9,801 м / с) ²; 30 метров (98 футов)), оба из которых находятся около 39° северной широты. Измеренные значения можно получить из физических и математических таблиц Т.М. Ярвуда и Ф. Касла, Макмиллан, исправленное издание 1970 г. ^[17]

Ускорение под действием силы тяжести в различных городах
Расположение	РС ²	фут/с ²	Расположение	РС ²	фут/с ²	Расположение	РС ²	фут/с ²	Расположение	РС ²	фут/с ²
Анкоридж	9.826	32.24	Хельсинки	9.825	32.23	Осло	9.825	32.23	Копенгаген	9.821	32.22
Стокгольм	9.818	32.21	Манчестер	9.818	32.21	Амстердам	9.817	32.21	Котагири	9.817	32.21
Бирмингем	9.817	32.21	Лондон	9.816	32.20	Брюссель	9.815	32.20	Франкфурт	9.814	32.20
Сиэтл	9.811	32.19	Париж	9.809	32.18	Монреаль	9.809	32.18	Ванкувер	9.809	32.18
Стамбул	9.808	32.18	Торонто	9.807	32.18	Цюрих	9.807	32.18	Оттава	9.806	32.17
Скопье	9.804	32.17	Чикаго	9.804	32.17	Рим	9.803	32.16	Веллингтон	9.803	32.16
Нью-Йорк	9.802	32.16	Лиссабон	9.801	32.16	Вашингтон	9.801	32.16	Афины	9.800	32.15
Мадрид	9.800	32.15	Мельбурн	9.800	32.15	Окленд	9.799	32.15	Денвер	9.798	32.15
Токио	9.798	32.15	Буэнос айрес	9.797	32.14	Сидней	9.797	32.14	Никосия	9.797	32.14
Ангелы	9.796	32.14	Кейптаун	9.796	32.14	Перт	9.794	32.13	Кувейт	9.792	32.13
Тайбэй	9.790	32.12	Рио де Жанейро	9.788	32.11	Гавана	9.786	32.11	Калькутта	9.785	32.10
Гонконг	9.785	32.10	Бангкок	9.780	32.09	Манила	9.780	32.09	Джакарта	9.777	32.08
Куала-Лумпур	9.776	32.07	Сингапур	9.776	32.07	Мехико	9.776	32.07	Канди	9.775	32.07

Математические модели [ править ]

Если местность находится на уровне моря, мы можем оценить для Геодезической справочной системы 1980 года: $g\{\phi \}$ , ускорение на широте $\phi$ :

{\begin{aligned}g\{\phi \}&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1+0.0053024\,\sin ^{2}\phi -0.0000058\,\sin ^{2}2\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1+0.0052792\,\sin ^{2}\phi +0.0000232\,\sin ^{4}\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1.0053024-0.0053256\,\cos ^{2}\phi +0.0000232\,\cos ^{4}\phi \right),\\&=9.780327\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\,\,\left(1.0026454-0.0026512\,\cos 2\phi +0.0000058\,\cos ^{2}2\phi \right)\end{aligned}}

Это Международная формула гравитации 1967 года, Формула геодезической системы отсчета 1967 года, уравнение Гельмерта или формула Клеро . ^[18]

Альтернативной формулой для g как функции широты является WGS ( Всемирной геодезической системы формула эллипсоидальной гравитации ) 84 : ^[19]

g\{\phi \}=\mathbb {G} _{e}\left[{\frac {1+k\sin ^{2}\phi }{\sqrt {1-e^{2}\sin ^{2}\phi }}}\right],\,\!

где,

$a,\,b$ – экваториальная и полярная полуоси соответственно;
$e^{2}=1-(b/a)^{2}$ сфероида – эксцентриситет , возведенный в квадрат;
$\mathbb {G} _{e},\,\mathbb {G} _{p}\,$ – определенная сила тяжести на экваторе и полюсах соответственно;
$k={\frac {b\,\mathbb {G} _{p}-a\,\mathbb {G} _{e}}{a\,\mathbb {G} _{e}}}$ (константа формулы);

Тогда где $\mathbb {G} _{p}=9.8321849378\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}$ , ^[19]

g\{\phi \}=9.7803253359\,\,\mathrm {m} \cdot \mathrm {s} ^{-2}\left[{\frac {1+0.001931852652\,\sin ^{2}\phi }{\sqrt {1-0.0066943799901\,\sin ^{2}\phi }}}\right]

.

где полуоси земли:

a=6378137.0\,\,{\mbox{m}}

b=6356752.314245\,\,{\mbox{m}}

Разница между формулой WGS-84 и уравнением Гельмерта составляет менее 0,68 мкм·с. ⁻².

Дальнейшие сокращения применяются для получения гравитационных аномалий (см.: Гравитационная аномалия#Вычисление ).

Оценка g закона тяготения из всемирного

Согласно закону всемирного тяготения , сила, действующая на тело, на которую действует сила гравитации Земли, определяется выражением

F=G{\frac {m_{1}m_{2}}{r^{2}}}=\left(G{\frac {M_{\oplus }}{r^{2}}}\right)m

где r — расстояние между центром Земли и телом (см. ниже), и здесь мы принимаем $M_{\oplus }$ быть массой Земли, а m — массой тела.

Кроме того, Ньютона второй закон F = ma , где m — масса, а a — ускорение, говорит нам, что

F=mg

Сравнивая две формулы, видно, что:

g=G{\frac {M_{\oplus }}{r^{2}}}

Итак, чтобы найти ускорение свободного падения на уровне моря, подставьте значения гравитационной постоянной , G Земли массы (в килограммах) м ₁ Земли и радиуса (в метрах) r , чтобы получить значение г : ^[20]

g=G{\frac {M_{\oplus }}{r^{2}}}=6.674\cdot 10^{-11}\mathrm {{m}^{3}\,{kg}^{-1}{s}^{-2}} \times {\frac {6\times 10^{24}\mathrm {kg} }{(6.4\times 10^{6}\mathrm {m} )^{2}}}=9+{\frac {795}{2^{10}}}\approx 9.77637\,\mathrm {{m}\,{s}^{-2}}

Эта формула работает только благодаря тому математическому факту, что гравитация однородного сферического тела, измеренная на его поверхности или над ней, такая же, как если бы вся его масса была сосредоточена в точке в его центре. Это то, что позволяет нам использовать радиус Земли в качестве r .

Полученное значение примерно согласуется с измеренным значением g . Эту разницу можно объяснить несколькими факторами, упомянутыми выше в разделе « Изменение величины »:

Земля не однородна
Земля не является идеальной сферой, и для ее радиуса необходимо использовать среднее значение.
Это расчетное значение g включает только истинную гравитацию. Сюда не входит уменьшение силы притяжения, которое мы воспринимаем как уменьшение гравитации из-за вращения Земли, а также некоторое противодействие гравитации центробежной силой.

Существуют значительные неопределенности в значениях r и m ₁ , используемых в этом расчете, а значение G также довольно сложно точно измерить.

Если известны G , g и r , то обратный расчет даст оценку массы Земли. Этот метод использовал Генри Кавендиш .

Измерение [ править ]

Измерение гравитации Земли называется гравиметрией .

Спутниковые измерения [ править ]

В настоящее время статические и переменные во времени параметры гравитационного поля Земли определяются с помощью современных спутниковых миссий, таких как GOCE , CHAMP , Swarm , GRACE и GRACE-FO . ^[21]^[22] Параметры низшей степени, включая сжатие Земли и движение геоцентра, лучше всего определять с помощью спутниковой лазерной локации . ^[23]

Крупномасштабные гравитационные аномалии могут быть обнаружены из космоса как побочный продукт спутниковых гравитационных миссий, например, GOCE . Эти спутниковые миссии направлены на восстановление подробной модели гравитационного поля Земли, обычно представляемой в форме сферически-гармонического расширения гравитационного потенциала Земли, но также возможны альтернативные представления, такие как карты волн геоида или гравитационные аномалии. произведено.

Эксперимент по восстановлению гравитации и климату (GRACE) состоит из двух спутников, которые могут обнаруживать гравитационные изменения на Земле. Также эти изменения можно представить как временные вариации гравитационной аномалии. Лаборатория гравитационного восстановления и внутренних процессов (GRAIL) также состояла из двух космических кораблей, вращающихся вокруг Луны, которые находились на орбите Луны в течение трех лет, прежде чем сошли с орбиты в 2015 году.

См. также [ править ]

Скорость убегания - понятие небесной механики.
- Выход из атмосферы - потеря планетарных атмосферных газов в космическое пространство.
Фигура Земли . Размер и форма, используемые для моделирования Земли в геодезии.
Геопотенциал - энергия, связанная с гравитацией Земли.
- Геопотенциальная модель - Теоретическое описание гравиметрической формы Земли.
- Аномалия Бугера - тип гравитационной аномалии.
Гравитация Луны
Гравитационное ускорение - изменение скорости только под действием силы тяжести.
Гравитация – Притяжение масс и энергии.
Аномалия гравитации - разница между идеальным и наблюдаемым гравитационным ускорением в определенном месте.
Гравитация Марса - Гравитационная сила планеты Марс.
Закон всемирного тяготения Ньютона - Классическое утверждение гравитации как силы
Вертикальное отклонение - мера смещения гравитационной силы вниз из-за близлежащей массы.

Ссылки [ править ]

^ НАСА/Лаборатория реактивного движения/Центр космических исследований Техасского университета. «PIA12146: Анимация глобальной гравитации GRACE» . Фотожурнал . Лаборатория реактивного движения НАСА . Проверено 30 декабря 2013 г.
^ Перейти обратно: ^а ^б Бойнтон, Ричард (2001). « Точное измерение массы » (PDF) . Бумага Саве № 3147 . Арлингтон, Техас: SAWE, Inc. Архивировано из оригинала (PDF) 27 февраля 2007 года . Проверено 22 декабря 2023 г.
^ Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Спрингер. ISBN 978-3-211-33544-4 . § 2.1: «Суммарная сила, действующая на тело, покоящееся на земной поверхности, является равнодействующей силы гравитации и центробежной силы вращения Земли и называется гравитацией».
^ Международное бюро мер и весов (1901 г.). «Положение, касающееся единицы массы и определения веса; условное значение $г н$ ». Отчеты сессий Третьей Генеральной конференции мер и весов (на французском языке). Париж: Готье-Виллар. п. 68. Число, принятое Международной службой мер и весов для значения нормального ускорения свободного падения, составляет 980,665 см/сек², число, уже санкционированное некоторыми законами. Декларация, касающаяся единицы массы и определения веса; условное значение $g n$ .
^ Мориц, Гельмут (2000). «Геодезическая справочная система 1980 года» . Журнал геодезии . 74 (1): 128–133. дои : 10.1007/s001900050278 . S2CID 195290884 . Проверено 26 июля 2023 г. γe = 9,780 326 7715 м/с² нормальная сила тяжести на экваторе
^ Хирт, Кристиан; Классенс, Стен; Фехер, Томас; Кун, Майкл; Пейл, Роланд; Рексер, Мориц (28 августа 2013 г.). «Новая картина гравитационного поля Земли в сверхвысоком разрешении». Письма о геофизических исследованиях . 40 (16): 4279–4283. Бибкод : 2013GeoRL..40.4279H . дои : 10.1002/grl.50838 . hdl : 20.500.11937/46786 . S2CID 54867946 .
^ "Wolfram | Alpha Gravity в Куала-Лумпуре", Wolfram Alpha, по состоянию на ноябрь 2020 г.
^ Терри Куинн (2011). От артефактов к атомам: BIPM и поиск окончательных эталонов измерений . Издательство Оксфордского университета . п. 127. ИСБН 978-0-19-530786-3 .
^ Разрешение 3-й ГКМВ (1901 г.), стр. 70 (в см/с). ²). МБМВ – Резолюция 3-й ГКМВ
^ «Интересно, что касается астрономии?» . Cornell University . Архивировано из оригинала 28 июля 2013 года . Проверено 22 декабря 2023 г.
^ "Я чувствую себя легче, когда поднимаюсь на гору, но не так ли?" , Часто задаваемые вопросы Национальной физической лаборатории
^ «G в машине» , НАСА, см. «Примечание редактора № 2».
^ Перейти обратно: ^а ^б А. М. Дзевонски, Д. Л. Андерсон (1981). «Предварительная эталонная модель Земли» (PDF) . Физика Земли и недр планет . 25 (4): 297–356. Бибкод : 1981PEPI...25..297D . дои : 10.1016/0031-9201(81)90046-7 . ISSN 0031-9201 .
^ Типлер, Пол А. (1999). Физика для ученых и инженеров (4-е изд.). Нью-Йорк: WH Freeman/Worth Publishers. стр. 336–337. ISBN 9781572594913 .
^ Уоттс, AB; Дейли, Сан-Франциско (май 1981 г.). «Длинноволновая гравитация и топографические аномалии». Ежегодный обзор наук о Земле и планетах . 9 : 415–418. Бибкод : 1981AREPS...9..415W . doi : 10.1146/annurev.ea.09.050181.002215 .
↑ Виджет гравитационных полей по состоянию на 25 октября 2012 г. – WolframAlpha
^ Т. М. Ярвуд и Ф. Касл, Физические и математические таблицы , исправленное издание, Macmillan and Co LTD, Лондон и Бейзингсток, напечатано в Великобритании издательством The University Press, Глазго, 1970, стр. 22 и 23.
^ Международная формула гравитации. Архивировано 20 августа 2008 г. в Wayback Machine.
^ Перейти обратно: ^а ^б « Мировая геодезическая система Министерства обороны, 1984 г. - ее определение и взаимосвязь с местными геодезическими системами» , NIMA TR8350.2, 3-е изд., таблица 3.4, уравнение 4-1» (PDF) . Архивировано из оригинала (PDF) 11 апреля 2014 г. Проверено 15 октября 2015 г.
^ «Гравитация» . www.cert.nic . Проверено 25 января 2022 г.
^ Мейер, Ульрих; Сосница, Кшиштоф; Арнольд, Дэниел; Дале, Кристоф; Таллер, Даниэла; Дах, Рольф; Ягги, Адриан (22 апреля 2019 г.). «Определение и комбинация гравитационного поля SLR, GRACE и роя» . Дистанционное зондирование . 11 (8): 956. Бибкод : 2019RemS...11..956M . дои : 10.3390/rs11080956 . hdl : 10281/240694 .
^ Тэпли, Байрон Д.; Уоткинс, Майкл М.; Флехтнер, Франк; Рейгбер, Кристоф; Беттадпур, Шринивас; Роделл, Мэтью; Сасген, Инго; Фамильетти, Джеймс С.; Ландерер, Феликс В.; Чемберс, Дон П.; Ригер, Джон Т.; Гарднер, Алекс С.; Спаси, Химаншу; Айвинс, Эрик Р.; Свенсон, Шон К.; Бенинг, Кармен; Дале, Кристоф; Визе, Дэвид Н.; Добслав, Хенрик; Тамисия, Марк Э.; Великогна, Изабелла (май 2019 г.). «Вклад GRACE в понимание изменения климата» . Природа Изменение климата . 9 (5): 358–369. Бибкод : 2019NatCC...9..358T . дои : 10.1038/s41558-019-0456-2 . ПМК 6750016 . ПМИД 31534490 .
^ Сосьница, Кшиштоф; Ягги, Адриан; Мейер, Ульрих; Таллер, Даниэла; Бойтлер, Герхард; Арнольд, Дэниел; Дач, Рольф (октябрь 2015 г.). «Изменяемое во времени гравитационное поле Земли от спутников SLR» . Журнал геодезии . 89 (10): 945–960. Бибкод : 2015JGeod..89..945S . дои : 10.1007/s00190-015-0825-1 .

Внешние ссылки [ править ]

[1] НАСА/Лаборатория реактивного движения/Центр космических исследований Техасского университета. «PIA12146: Анимация глобальной гравитации GRACE» . Фотожурнал . Лаборатория реактивного движения НАСА . Проверено 30 декабря 2013 г.

[Boynton-2] Перейти обратно: ^а ^б Бойнтон, Ричард (2001). « Точное измерение массы » (PDF) . Бумага Саве № 3147 . Арлингтон, Техас: SAWE, Inc. Архивировано из оригинала (PDF) 27 февраля 2007 года . Проверено 22 декабря 2023 г.

[3] Хофманн-Велленхоф, Б.; Мориц, Х. (2006). Физическая геодезия (2-е изд.). Спрингер. ISBN 978-3-211-33544-4 . § 2.1: «Суммарная сила, действующая на тело, покоящееся на земной поверхности, является равнодействующей силы гравитации и центробежной силы вращения Земли и называется гравитацией».

[4] Международное бюро мер и весов (1901 г.). «Положение, касающееся единицы массы и определения веса; условное значение $г н$ ». Отчеты сессий Третьей Генеральной конференции мер и весов (на французском языке). Париж: Готье-Виллар. п. 68. Число, принятое Международной службой мер и весов для значения нормального ускорения свободного падения, составляет 980,665 см/сек², число, уже санкционированное некоторыми законами. Декларация, касающаяся единицы массы и определения веса; условное значение $g n$ .

[5] Мориц, Гельмут (2000). «Геодезическая справочная система 1980 года» . Журнал геодезии . 74 (1): 128–133. дои : 10.1007/s001900050278 . S2CID 195290884 . Проверено 26 июля 2023 г. γe = 9,780 326 7715 м/с² нормальная сила тяжести на экваторе

[6] Хирт, Кристиан; Классенс, Стен; Фехер, Томас; Кун, Майкл; Пейл, Роланд; Рексер, Мориц (28 августа 2013 г.). «Новая картина гравитационного поля Земли в сверхвысоком разрешении». Письма о геофизических исследованиях . 40 (16): 4279–4283. Бибкод : 2013GeoRL..40.4279H . дои : 10.1002/grl.50838 . hdl : 20.500.11937/46786 . S2CID 54867946 .

[Wolfram_Alpha-7] "Wolfram | Alpha Gravity в Куала-Лумпуре", Wolfram Alpha, по состоянию на ноябрь 2020 г.

[8] Терри Куинн (2011). От артефактов к атомам: BIPM и поиск окончательных эталонов измерений . Издательство Оксфордского университета . п. 127. ИСБН 978-0-19-530786-3 .

[9] Разрешение 3-й ГКМВ (1901 г.), стр. 70 (в см/с). ²). МБМВ – Резолюция 3-й ГКМВ

[10] «Интересно, что касается астрономии?» . Cornell University . Архивировано из оригинала 28 июля 2013 года . Проверено 22 декабря 2023 г.

[11] "Я чувствую себя легче, когда поднимаюсь на гору, но не так ли?" , Часто задаваемые вопросы Национальной физической лаборатории

[12] «G в машине» , НАСА, см. «Примечание редактора № 2».

[prem-13] Перейти обратно: ^а ^б А. М. Дзевонски, Д. Л. Андерсон (1981). «Предварительная эталонная модель Земли» (PDF) . Физика Земли и недр планет . 25 (4): 297–356. Бибкод : 1981PEPI...25..297D . дои : 10.1016/0031-9201(81)90046-7 . ISSN 0031-9201 .

[14] Типлер, Пол А. (1999). Физика для ученых и инженеров (4-е изд.). Нью-Йорк: WH Freeman/Worth Publishers. стр. 336–337. ISBN 9781572594913 .

[15] Уоттс, AB; Дейли, Сан-Франциско (май 1981 г.). «Длинноволновая гравитация и топографические аномалии». Ежегодный обзор наук о Земле и планетах . 9 : 415–418. Бибкод : 1981AREPS...9..415W . doi : 10.1146/annurev.ea.09.050181.002215 .

[wolfram-16] Виджет гравитационных полей по состоянию на 25 октября 2012 г. – WolframAlpha

[17] Т. М. Ярвуд и Ф. Касл, Физические и математические таблицы , исправленное издание, Macmillan and Co LTD, Лондон и Бейзингсток, напечатано в Великобритании издательством The University Press, Глазго, 1970, стр. 22 и 23.

[IGF-18] Международная формула гравитации. Архивировано 20 августа 2008 г. в Wayback Machine.

[DoD-WGS84-19] Перейти обратно: ^а ^б « Мировая геодезическая система Министерства обороны, 1984 г. - ее определение и взаимосвязь с местными геодезическими системами» , NIMA TR8350.2, 3-е изд., таблица 3.4, уравнение 4-1» (PDF) . Архивировано из оригинала (PDF) 11 апреля 2014 г. Проверено 15 октября 2015 г.

[20] «Гравитация» . www.cert.nic . Проверено 25 января 2022 г.

[21] Мейер, Ульрих; Сосница, Кшиштоф; Арнольд, Дэниел; Дале, Кристоф; Таллер, Даниэла; Дах, Рольф; Ягги, Адриан (22 апреля 2019 г.). «Определение и комбинация гравитационного поля SLR, GRACE и роя» . Дистанционное зондирование . 11 (8): 956. Бибкод : 2019RemS...11..956M . дои : 10.3390/rs11080956 . hdl : 10281/240694 .

[22] Тэпли, Байрон Д.; Уоткинс, Майкл М.; Флехтнер, Франк; Рейгбер, Кристоф; Беттадпур, Шринивас; Роделл, Мэтью; Сасген, Инго; Фамильетти, Джеймс С.; Ландерер, Феликс В.; Чемберс, Дон П.; Ригер, Джон Т.; Гарднер, Алекс С.; Спаси, Химаншу; Айвинс, Эрик Р.; Свенсон, Шон К.; Бенинг, Кармен; Дале, Кристоф; Визе, Дэвид Н.; Добслав, Хенрик; Тамисия, Марк Э.; Великогна, Изабелла (май 2019 г.). «Вклад GRACE в понимание изменения климата» . Природа Изменение климата . 9 (5): 358–369. Бибкод : 2019NatCC...9..358T . дои : 10.1038/s41558-019-0456-2 . ПМК 6750016 . ПМИД 31534490 .

[23] Сосьница, Кшиштоф; Ягги, Адриан; Мейер, Ульрих; Таллер, Даниэла; Бойтлер, Герхард; Арнольд, Дэниел; Дач, Рольф (октябрь 2015 г.). «Изменяемое во времени гравитационное поле Земли от спутников SLR» . Журнал геодезии . 89 (10): 945–960. Бибкод : 2015JGeod..89..945S . дои : 10.1007/s00190-015-0825-1 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

v т Это Геодезия
Overview	History Geodesists
Subfields	Cartography Computer cartography Web mapping Earth's orbit Geodetic astronomy Geomatics Gravity of Earth Navigation Photogrammetry Remote Sensing Geopositioning Virtual globe
Physical phenomena	Chandler wobble Coriolis effect Earth's energy budget Earth's gravity field Geodynamo Gravity of Earth Plate tectonics Precession of the equinoxes Tide
Related disciplines	Astronomy Geology Geophysics Mathematics Physics
Geodesy portal Category Commons

v т Это Геофизика
Overview	Outline Geophysicists
Subfields	Geodynamics Geophysical survey Geomagnetism Geomathematics Geophysical fluid dynamics Mineral physics Near-surface geophysics Paleomagnetism Seismology Tectonophysics
Physical phenomena	Chandler wobble Coriolis effect Earth's energy budget Earth's magnetic field Geodynamo Geothermal gradient Gravity of Earth Mantle convection Precession of the equinoxes Seismic wave Tide
Related disciplines	Geodesy
Geophysics portal Category Commons

v т Это Земля
Outline History
Atmosphere	Atmosphere of Earth Prebiotic atmosphere Troposphere Stratosphere Mesosphere Thermosphere Exosphere Weather
Climate	Climate system Energy balance Climate change Climate variability and change Climatology Paleoclimatology
Continents	Africa Antarctica Asia Australia Europe North America South America
Culture and society	List of sovereign states dependent territories In culture Earth Day Flag Symbol World economy Etymology World history Time zones World
Environment	Biome Biosphere Biogeochemical cycles Ecology Ecosystem Human impact on the environment Evolutionary history of life Nature
Geodesy	Cartography Computer cartography Earth's orbit Geodetic astronomy Geomatics Gravity Navigation Remote Sensing Geopositioning Virtual globe
Geophysics	Earth structure Fluid dynamics Geomagnetism Magnetosphere Mineral physics Seismology Plate tectonics Signal processing Tomography
Geology	Age of Earth Earth science Extremes on Earth Future Geological history Geologic time scale Geologic record History of Earth
Oceans	Antarctic/Southern Ocean Arctic Ocean Atlantic Ocean Indian Ocean Pacific Ocean Oceanography
Natural satellite	Moon
Planetary science	Evolution of the Solar System Geology of solar terrestrial planets Location in the Universe Solar System
Category