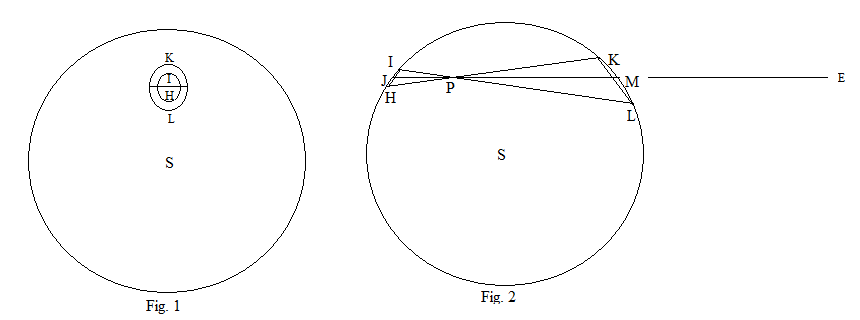
Теорема оболочки

В классической механике теорема о оболочках дает гравитационные упрощения, которые можно применять к объектам внутри или снаружи сферически симметричного тела. Эта теорема имеет особое применение в астрономии .

Исаак Ньютон доказал теорему о оболочках и заявил, что:

1. Сферически тело действует на внешние объекты гравитационно , симметричное как будто вся его масса сосредоточена в точке в его центре.
2. Если тело представляет собой сферически-симметричную оболочку (т. е. полый шар), оболочка не оказывает никакого суммарного гравитационного воздействия на какой-либо объект внутри оболочки, независимо от местоположения объекта внутри оболочки.

Следствием этого является то, что внутри твердой сферы постоянной плотности сила гравитации внутри объекта изменяется линейно с расстоянием от центра, становясь нулевой из-за симметрии в центре масс . Это можно увидеть так: возьмем точку внутри такой сферы, на расстоянии $r$ от центра сферы. Тогда можно игнорировать все оболочки большего радиуса согласно теореме о оболочках (2). Но точку можно считать внешней по отношению к остальной сфере радиуса r, и согласно (1) всю массу этой сферы можно считать сосредоточенной в ее центре. Оставшаяся масса $m$ пропорционально $r^{3}$ (потому что это основано на объеме). Сила гравитации, действующая на тело радиуса r, будет пропорциональна $m/r^{2}$ ( закон обратных квадратов ), поэтому общий гравитационный эффект пропорционален $r^{3}/r^{2}=r$, поэтому линейно по $r$.

Эти результаты были важны для анализа движения планет Ньютоном; они не очевидны сразу, но их можно доказать с помощью математических вычислений . ( Закон Гаусса для гравитации предлагает альтернативный способ формулировки теоремы.)

В дополнение к гравитации , теорема оболочки может также использоваться для описания электрического поля, создаваемого статической сферически-симметричной плотностью заряда , или аналогичным образом для любого другого явления, которое подчиняется закону обратных квадратов . Выводы, приведенные ниже, сосредоточены на гравитации, но результаты можно легко обобщить на электростатическую силу .

Вывод гравитационного поля вне твердой сферы

Доказательство теоремы Ньютона о оболочках (1) состоит из трех шагов. Сначала будет выведено уравнение для гравитационного поля, создаваемого кольцом масс. Если составить диск из бесконечного числа бесконечно тонких колец, это уравнение, включающее кольцо, будет использоваться для нахождения гравитационного поля, создаваемого диском. Наконец, если из бесконечного числа бесконечно тонких дисков составить сферу, это уравнение, включающее диск, будет использоваться для нахождения гравитационного поля, создаваемого сферой.

Гравитационное поле $E$ на позиции под названием $P$ в $(x,y)=(-p,0)$ по оси x из-за точки массы $M$ в начале находится

$$E_{\text{point}}={\frac {GM}{p^{2}}}$$

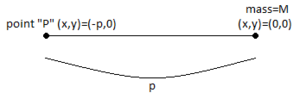Предположим, что эта масса перемещена вверх по оси y до точки $(-p,R)$. Расстояние между $P$ и точечная масса теперь длиннее, чем раньше; Она становится гипотенузой прямоугольного треугольника с катетами. $p$ и $R$ который ${\textstyle {\sqrt {p^{2}+R^{2}}}}$. Следовательно, гравитационное поле возвышенной точки равно: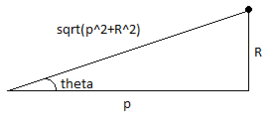

$$E_{\text{elevated point}}={\frac {GM}{p^{2}+R^{2}}}$$

Величина гравитационного поля, которое притягивает частицу в точке $P$ в направлении x — это гравитационное поле, умноженное на $\cos(\theta )$ где $\theta$ — угол, прилегающий к оси x . В этом случае, $\cos(\theta )={\frac {p}{\sqrt {p^{2}+R^{2}}}}$. Следовательно, величина гравитационного поля в направлении x , $E_{x}$ является:

$$E_{x}={\frac {GM\cos {\theta }}{p^{2}+R^{2}}}$$

Подстановка в $\cos(\theta )$ дает

$$E_{x}={\frac {GMp}{\left(p^{2}+R^{2}\right)^{3/2}}}$$

Предположим, что эта масса равномерно распределена в кольце с центром в начале координат и обращенной к нему точке. $P$ с тем же радиусом $R$. Поскольку вся масса расположена под одним и тем же углом по отношению к оси x , а расстояние между точками на кольце такое же, как и раньше, гравитационное поле в направлении x в точке $P$ благодаря кольцу - это то же самое, что и точечная масса, находящаяся в точке $R$ единицы выше оси Y :

$$E_{\text{ring}}={\frac {GMp}{\left(p^{2}+R^{2}\right)^{3/2}}}$$

Чтобы найти гравитационное поле в точке $P$ благодаря диску обращено бесконечное количество бесконечно тонких колец $P$, каждый с радиусом $y$, ширина $dy$, и масса $dM$ могут быть помещены друг в друга, образуя диск. Масса любого из колец $dM$ - масса диска, умноженная на отношение площади кольца $2\pi y\,dy$ к общей площади диска $\pi R^{2}$. Так, ${\textstyle dM={\frac {M\cdot 2y\,dy}{R^{2}}}}$. Следовательно, небольшое изменение гравитационного поля, $E$ является:

$$dE={\frac {Gp\,dM}{(p^{2}+y^{2})^{3/2}}}$$

Подстановка в $dM$ а интегрирование обеих сторон дает гравитационное поле диска:

$$E=\int {\frac {GMp\cdot {\frac {2y\,dy}{R^{2}}}}{(p^{2}+y^{2})^{3/2}}}$$

Сложение вклада в гравитационное поле от каждого из этих колец даст выражение для гравитационного поля, создаваемого диском. Это эквивалентно интегрированию приведенного выше выражения из $y=0$ к $y=R$, в результате чего:

$$E_{\text{disc}}={\frac {2GM}{R^{2}}}\left(1-{\frac {p}{\sqrt {p^{2}+R^{2}}}}\right)$$

Найти гравитационное поле в точке $P$ из-за сферы с центром в начале координат бесконечное количество бесконечно тонких дисков, обращенных $P$, каждый с радиусом $R$, ширина $dx$, и масса $dM$ можно разместить вместе.

Радиусы этих дисков $R$ следить за высотой поперечного сечения сферы (с постоянным радиусом $a$) которое представляет собой уравнение полукруга: ${\textstyle R={\sqrt {a^{2}-x^{2}}}}$. $x$ варьируется от $-a$ к $a$.

Масса любого из дисков $dM$ это масса сферы $M$ умноженный на отношение объема бесконечно тонкого диска к объему сферы (с постоянным радиусом $a$). Объем бесконечно тонкого диска равен $\pi R^{2}\,dx$, или ${\textstyle \pi \left(a^{2}-x^{2}\right)dx}$. Так, ${\textstyle dM={\frac {\pi M(a^{2}-x^{2})\,dx}{{\frac {4}{3}}\pi a^{3}}}}$. Упрощение дает ${\textstyle dM={\frac {3M(a^{2}-x^{2})\,dx}{4a^{3}}}}$.

Положение каждого диска вдали от $P$ будет меняться в зависимости от его положения внутри «сферы», состоящей из дисков, поэтому $p$ необходимо заменить на $p+x$.

Замена $M$ с $dM$, $R$ с ${\sqrt {a^{2}-x^{2}}}$, и $p$ с $p+x$ в уравнении «диска» дает:

$$dE={\frac {\left({\frac {2G\left[3M\left(a^{2}-x^{2}\right)\right]}{4a^{3}}}\right)}{{\sqrt {a^{2}-x^{2}}}^{2}}}\cdot \left(1-{\frac {p+x}{\sqrt {(p+x)^{2}+{\sqrt {a^{2}-x^{2}}}^{2}}}}\right)\,dx$$

Упрощая,

$$\int dE=\int _{-a}^{a}{\frac {3GM}{2a^{3}}}\left(1-{\frac {p+x}{\sqrt {p^{2}+a^{2}+2px}}}\right)dx$$

Интегрирование гравитационного поля каждого тонкого диска из $x=-a$ к $x=+a$ относительно $x$и , тщательно выполнив алгебраические действия, получаем теорему Ньютона о оболочках:

$$E={\frac {GM}{p^{2}}}$$

где $p$ - расстояние между центром сферической массы и произвольной точкой $P$. Гравитационное поле сферической массы можно рассчитать, рассматривая всю массу как точечную частицу в центре сферы.

Вне оболочки

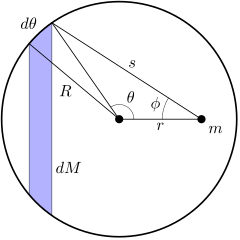
Твердое сферически симметричное тело можно смоделировать как бесконечное количество концентрических бесконечно тонких сферических оболочек. Если одну из этих оболочек можно рассматривать как точечную массу, то и систему оболочек (т.е. сферу) также можно рассматривать как точечную массу. Рассмотрим одну такую ​​оболочку (на схеме показано поперечное сечение):

(Примечание: $d\theta$ на диаграмме имеется в виду малый угол, а не длина дуги . Длина дуги ${\textstyle R\,d\theta }$.)

Применяя универсальный закон гравитации Ньютона , сумма сил, действующих на элементы массы в заштрихованной полосе, равна

$dF={\frac {Gm}{s^{2}}}dM.$

Однако, поскольку происходит частичная компенсация из-за векторной природы силы в сочетании с симметрией круговой полосы, оставшаяся компонента (в направлении, указывающем на $m$) определяется

$dF_{r}={\frac {Gm}{s^{2}}}\cos(\varphi )\,dM$

Суммарная сила на $m$Тогда это просто сумма сил, действующих со стороны всех полос. Уменьшив ширину каждой полосы и увеличив количество полос, сумма становится целым выражением:

$F_{r}=\int dF_{r}$

С $G$ и $m$ являются константами, их можно вынести из интеграла:

$F_{r}=Gm\int {\frac {\cos(\varphi )}{s^{2}}}\,dM.$

Чтобы вычислить этот интеграл, нужно сначала выразить $dM$ как функция $d\theta$

Полная поверхность сферической оболочки равна

$4\pi R^{2}$

в то время как площадь поверхности тонкого среза между $\theta$ и $\theta +d\theta$ является

$2\pi R\sin(\theta )R\,d\theta =2\pi R^{2}\sin(\theta )\,d\theta$

Если масса снаряда $M$, следовательно, имеем это

$dM={\frac {2\pi R^{2}\sin(\theta )}{4\pi R^{2}}}M\,d\theta ={\frac {1}{2}}M\sin(\theta )\,d\theta$

и

$F_{r}={\frac {GMm}{2}}\int {\frac {\sin(\theta )\cos(\varphi )}{s^{2}}}\,d\theta$

По закону косинусов ,

$\cos(\varphi )={\frac {r^{2}+s^{2}-R^{2}}{2rs}}$

и

$\cos(\theta )={\frac {r^{2}+R^{2}-s^{2}}{2rR}}.$

Эти два отношения связывают три параметра $\theta$, $\varphi$ и $s$ которые входят в интеграл вместе. Как $\theta$ увеличивается с $0$ к $\pi$ радианы, $\varphi$ варьируется от начального значения 0 до максимального значения, а затем, наконец, возвращается к нулю при $\theta =\pi$. В то же время, $s$ увеличивается от первоначального значения $r-R$ до окончательного значения $r+R$ как $\theta$ увеличивается от 0 до $\pi$ радианы. Это иллюстрируется следующей анимацией:

(Примечание: если смотреть со стороны $m$, заштрихованная синяя полоса выглядит как тонкое кольцо, внутренний и внешний радиусы которого сходятся к $R\sin(\theta )$ как $d\theta$ исчезает.)

Чтобы найти примитивную функцию для подынтегрального выражения, нужно сделать $s$ независимая переменная интегрирования вместо $\theta$.

Выполнение неявного дифференцирования второго из приведенных выше выражений «закона косинуса» дает

$-\sin(\theta )\,d\theta ={\frac {-2s}{2rR}}\,ds$

и таким образом

$\sin(\theta )\,d\theta ={\frac {s}{rR}}\,ds.$

Отсюда следует, что

$F_{r}={\frac {GMm}{2}}{\frac {1}{rR}}\int {\frac {s\cos(\varphi )}{s^{2}}}\,ds={\frac {GMm}{2rR}}\int {\frac {\cos(\varphi )}{s}}\,ds$

где новая переменная интегрирования $s$ увеличивается с $r-R$ к $r+R$.

Вставив выражение для $\cos(\varphi )$ используя первое из приведенных выше выражений «закона косинуса», в конце концов получаем, что

$F_{r}={\frac {GMm}{4r^{2}R}}\int \left(1+{\frac {r^{2}-R^{2}}{s^{2}}}\right)\ ds\ .$

Примитивной функцией для подынтегральной функции является

$s-{\frac {r^{2}-R^{2}}{s}}\ ,$

и вставляем границы $r-R$ и $r+R$ для переменной интегрирования $s$ в этой примитивной функции получается, что

$F_{r}={\frac {GMm}{r^{2}}},$

говоря, что сила гравитации такая же, как и у точечной массы в центре оболочки с той же массой.

От сферической оболочки к твердой сфере

Этот результат сферической оболочки можно использовать для повторного получения ранее полученного результата твердой сферы. Это достигается путем объединения бесконечно тонкой сферической оболочки с массой $dM$, и мы можем получить общий вклад силы тяжести твердого шара в объект вне шара

$F_{total}=\int dF_{r}={\frac {Gm}{r^{2}}}\int dM.$

Равномерная плотность означает, что между радиусом $x$ к $x+dx$, $dM$ может быть выражено как функция $x$, то есть,

$dM={\frac {4\pi x^{2}dx}{{\frac {4}{3}}\pi R^{3}}}M={\frac {3Mx^{2}dx}{R^{3}}}$

Следовательно, полная сила тяжести равна

$F_{\text{total}}={\frac {3GMm}{r^{2}R^{3}}}\int _{0}^{R}x^{2}\,dx={\frac {GMm}{r^{2}}}$

Как было обнаружено ранее, это предполагает, что гравитацию твердого сферического шара к внешнему объекту можно упростить, как гравитацию точечной массы в центре шара с той же массой.

Внутри оболочки

Для точки внутри оболочки разница состоит в том, что когда θ равно нулю, φ принимает значение π радиан, а s — значение R − r . Когда θ увеличивается от 0 до π радиан, φ уменьшается от начального значения π радиан до нуля, а s увеличивается от начального значения R − r до значения R + r .

Все это можно увидеть на следующем рисунке

Вставка этих границ в примитивную функцию

$s-{\frac {r^{2}-R^{2}}{s}}$

в данном случае это получается

$F_{r}=0,$

говоря, что чистые гравитационные силы, действующие на точечную массу со стороны элементов массы оболочки за пределами точки измерения, уравновешиваются.

Обобщение: если $f={\frac {k}{r^{p}}}$результирующая сила внутри оболочки равна:

$F(r)={\frac {GMm}{4r^{2}R}}\int _{R-r}^{R+r}\left({\frac {1}{s^{p-2}}}+{\frac {r^{2}-R^{2}}{s^{p}}}\right)\,ds$

Вышеупомянутое приводит к $F(r)$ тождественно нулю тогда и только тогда, когда $p=2$

Вне оболочки (т. $r>R$ или $r<-R$):

$F(r)={\frac {GMm}{4r^{2}R}}\int _{r-R}^{r+R}\left({\frac {1}{s^{p-2}}}+{\frac {r^{2}-R^{2}}{s^{p}}}\right)\,ds$

Гаусса

Теорема о оболочках является непосредственным следствием закона гравитации Гаусса , согласно которому

$\int _{S}{\mathbf {g} }\cdot \,d{\mathbf {S} }=-4\pi GM$

где M — масса части сферически-симметричного распределения массы, находящейся внутри сферы радиуса r и

$\int _{S}{\mathbf {g} }\cdot \,d{\mathbf {S} }=\int _{S}{\mathbf {g} }\cdot {\hat {\mathbf {n} }}\,dS$

- поверхностный интеграл гравитационного поля $\mathbf {g}$ над любой замкнутой поверхностью, внутри которой общая масса равна M , единичный вектор ${\hat {\mathbf {n} }}$ является внешней нормалью к поверхности.

Гравитационное поле сферически-симметричного распределения массы, такого как массовая точка, сферическая оболочка или однородная сфера, также должно быть сферически-симметричным. Если ${\hat {\mathbf {n} }}$ является единичным вектором в направлении от точки симметрии к другой точке, поэтому гравитационное поле в этой другой точке должно быть

$\mathbf {g} =g(r){\hat {\mathbf {n} }}$

где g ( r ) зависит только от расстояния r до точки симметрии

Выбрав замкнутую поверхность в виде сферы радиуса r с центром в точке симметрии, внешней нормали к точке на поверхности, ${\hat {\mathbf {n} }}$, - это именно направление, направленное от точки симметрии распределения массы.

Следовательно, у человека есть это

$\mathbf {g} =g(r){\hat {\mathbf {n} }}$

и

$\int _{S}\mathbf {g} \cdot \,d{\mathbf {S} }=g(r)\int _{S}\,dS=g(r)4\pi r^{2}$

так как площадь сферы равна 4 π r ² .

Тогда из закона Гаусса следует, что

$g(r)4\pi r^{2}=-4\pi GM,$

или,

$g(r)=-{\frac {GM}{r^{2}}}.$

Разговоры и обобщения

Естественно задаться вопросом, верно ли обратное утверждение теоремы о оболочке, а именно, следует ли из результата теоремы закон всемирного тяготения или существует ли какой-то более общий силовой закон, для которого теорема верна. Более конкретно можно задать вопрос:

Предположим, существует сила $F$ между массами M и m , разделенными расстоянием r вида $F=Mmf(r)$ так что любое сферически-симметричное тело воздействует на внешние тела так, как если бы его масса была сосредоточена в его центре. Тогда какой вид может иметь функция $f$ брать?

Фактически, это допускает ровно еще один класс силы, чем (ньютоновский) обратный квадрат. Самая общая сила, выведенная Ваге Гурзадяном в Теорема Гурзадяна :

$F=-{\frac {GMm}{r^{2}}}+{\frac {\Lambda mc^{2}r}{3}}$

где $G$ и $\Lambda$ могут быть константами, принимающими любое значение. Первый член — это знакомый закон всемирного тяготения; вторая — дополнительная сила, аналогичная космологической постоянной в общей теории относительности .

Если мы дополнительно ограничим силу, потребовав, чтобы также выполнялась вторая часть теоремы, а именно, чтобы внутри полого шара не было силы, мы исключим возможность дополнительного члена, и закон обратных квадратов действительно является уникальным законом силы, удовлетворяющим теорема.

С другой стороны, если мы ослабим условия и потребуем только того, чтобы поле повсюду вне сферически симметричного тела было таким же, как поле некоторой точечной массы в центре (любой массы), мы допускаем новый класс решений, заданный потенциалом Юкавы , частным случаем которого является закон обратных квадратов.

Еще одно обобщение можно сделать для диска, заметив, что

$dM={\frac {R^{2}}{2}}{\frac {d\theta \,\sin ^{2}(\theta )}{\pi R^{2}}}M={\frac {\sin ^{2}(\theta )}{2\pi }}M\,d\theta$

так:

$F_{r}={\frac {GMm}{2\pi }}\int {\frac {\sin ^{2}(\theta )\cos(\varphi )}{s^{2}}}\,d\theta ,$

где $M=\pi R^{2}\rho$, и $\rho$ это плотность тела.

Проделав все промежуточные вычисления, получим:

$F(r)={\frac {Gm\rho }{8r^{3}}}\int _{R-r}^{R+r}{\frac {\left(r^{2}+s^{2}-R^{2}\right){\sqrt {2\left(r^{2}R^{2}+r^{2}s^{2}+R^{2}s^{2}\right)-s^{4}-r^{4}-R^{4}}}}{s^{2}}}\,ds$

Доказательства Ньютона

Введение

В предложениях 70 и 71 рассматривается сила, действующая на частицу со стороны полой сферы с бесконечно тонкой поверхностью, массовая плотность которой постоянна по поверхности. Сила, действующая на частицу со стороны небольшого участка поверхности сферы, пропорциональна массе участка и обратно пропорциональна квадрату его расстояния от частицы. Первое предложение рассматривает случай, когда частица находится внутри сферы, второе — когда она находится снаружи. Использование бесконечно малых и предельных процессов в геометрических конструкциях просто и элегантно и позволяет избежать необходимости какого-либо интегрирования. Они хорошо иллюстрируют метод Ньютона для доказательства многих положений «Начал» .

Его доказательство предложения 70 тривиально. Далее оно рассматривается несколько более подробно, чем это дает Ньютон.

Доказательство предложения 71 имеет более историческое значение. Это составляет первую часть его доказательства того, что гравитационная сила твердой сферы, действующая на частицу вне ее, обратно пропорциональна квадрату ее расстояния от центра сферы, при условии, что плотность в любой точке внутри сферы является функцией только от его расстояния от центра сферы.

Хотя нижеследующие доказательства полностью соответствуют доказательствам Ньютона, в них были внесены очень незначительные изменения, чтобы сделать их более понятными.

Сила на точку внутри полой сферы

На рис. 2 показано сечение полой сферы через центр S и произвольную точку P внутри сферы. Через P проведите две линии IL и HK так, чтобы угол KPL был очень мал. JM — это линия, проходящая через P и делящая этот угол пополам. По теореме о вписанном угле треугольники IPH и KPL подобны. Линии KH и IL повернуты вокруг оси JM, образуя два конуса, пересекающие сферу по двум замкнутым кривым. На рис. 1 сфера видна издалека по линии PE и считается прозрачной, поэтому видны обе кривые.

Поверхность сферы, которую пересекают конусы, можно считать плоской, а $\angle PJI=\angle PMK$.

Поскольку пересечение конуса с плоскостью представляет собой эллипс, то в этом случае пересечения образуют два эллипса с большими осями IH и KL, где ${\frac {IH}{KL}}={\frac {PJ}{PM}}$.

По аналогичному аргументу меньшие оси находятся в одинаковом соотношении. Это ясно, если рассматривать сферу сверху. Следовательно, два эллипса подобны, поэтому их площади равны квадратам их больших осей. Поскольку масса любого участка поверхности пропорциональна площади этого сечения, для двух эллиптических площадей отношения их масс $\propto {\frac {PJ^{2}}{PM^{2}}}$.

Поскольку сила притяжения P в направлении JM от любой из эллиптических областей пропорциональна массе площади и обратно пропорциональна квадрату ее расстояния от P, она не зависит от расстояния P от сферы. Следовательно, силы, действующие на P со стороны двух бесконечно малых эллиптических областей, равны и противоположны, и в направлении JM нет результирующей силы.

Поскольку положение P и направление JM произвольны, из этого следует, что ни одна частица внутри полой сферы не испытывает результирующей силы со стороны массы сферы.

Примечание. Ньютон просто описывает дуги IH и KL как «минимально малые», а области, очерченные линиями IL и HK, могут иметь любую форму, не обязательно эллиптическую, но они всегда будут одинаковыми.

Сила, действующая на точку вне полой сферы

На рис. 1 показано поперечное сечение полой сферы через центр S с произвольной точкой P вне сферы. PT — это касательная к окружности в точке T, которая проходит через P. HI — небольшая дуга на поверхности, такая что PH меньше, чем PT. Продлите PI, чтобы пересечь сферу в точке L, и нарисуйте SF до точки F, которая делит IL пополам. Продлите PH так, чтобы пересечь сферу в точке K, и проведите SE до точки E, которая делит HK пополам, и продлите SF до пересечения HK в точке D. Опустите перпендикуляр IQ на линию PS, соединяющую точку P с центром S. Пусть радиус сферы быть a, а расстояние PS быть D.

Пусть дуга IH вытянута перпендикулярно из плоскости диаграммы на небольшое расстояние ζ. Площадь полученной фигуры равна $IH\cdot \zeta$, а его масса пропорциональна этому произведению.

Сила, действующая на частицу при P $\propto {\frac {IH\cdot \zeta }{PI^{2}}}$ и находится вдоль линии PI.

Составляющая этой силы по направлению к центру $\propto {\frac {IH\cdot PQ\cdot \zeta }{PI^{3}}}$.

Если теперь дугу HI полностью повернуть вокруг линии PS, чтобы образовать кольцо ширины HI и радиуса IQ , то длина кольца равна 2 π · IQ , а его площадь равна 2 π · IQ · IH . Компонента силы, действующей на частицу в точке P в направлении PS со стороны этого кольца, становится $\propto {\frac {IH\cdot IQ\cdot PQ}{PI^{3}}}$.

Перпендикулярные составляющие силы, направленные в сторону PS, компенсируются, поскольку масса в кольце распределяется симметрично относительно PS . Следовательно, составляющая в направлении PS представляет собой полную силу, действующую на P со стороны кольца, образованного вращением дуги HI вокруг PS .

Из подобных треугольников: ${\frac {IQ}{PI}}={\frac {FS}{D}}$; ${\frac {PQ}{PI}}={\frac {PF}{D}}$, и ${\frac {RI}{PI}}={\frac {DF}{PF}}$.

Если HI достаточно мало, чтобы его можно было принять за прямую линию, $\angle SIH$ представляет собой прямой угол, а $\angle RIH=\angle FIS$, так что ${\frac {HI}{RI}}={\frac {a}{IF}}$.

Следовательно, сила, действующая на P со стороны кольца $\propto {\frac {IH\cdot IQ\cdot PQ}{PI^{3}}}={\frac {a\cdot DF\cdot FS\cdot PF}{IF\cdot PF\cdot D\cdot D}}={\frac {a\cdot DF\cdot FS}{IF\cdot D^{2}}}$.

Предположим теперь, как показано на рис. 2, что другая частица находится вне сферы в точке p , на другом расстоянии d от центра сферы, причем соответствующие точки отмечены строчными буквами. Для удобства сравнения построение P на рис. 1 показано также на рис. 2. Как и раньше, ph меньше pt .

Создайте кольцо шириной ih и радиусом iq, составив угол $fiS=FIS$ и немного больший угол $dhS=DHS$, так что расстояние PS стягивается под тем же углом в I, что и pS в i. То же самое справедливо для H и h соответственно.

Полная сила, действующая на p, действующая на это кольцо, равна

$\propto {\frac {ih\cdot iq\cdot pq}{pi^{3}}}={\frac {a\cdot df\cdot fS}{if\cdot d^{2}}}$

Четко $fS=FS$, $if=IF$, и $eS=ES$.

Ньютон утверждает, что DF и df можно считать равными в пределе, когда углы DPF и dpf «вместе исчезают». Обратите внимание, что углы DPF и dpf не равны. Хотя DS и dS в пределе становятся равными, это не означает, что отношение DF к df становится равным единице, когда DF и df оба стремятся к нулю. В конечном случае DF зависит от D, а df от d, поэтому они не равны.

Поскольку отношение DF к df в пределе имеет решающее значение, требуется более детальный анализ. Из подобных прямоугольных треугольников ${\textstyle {\frac {DF}{PF}}={\frac {ED}{ES}}}$ и $ED^{2}=(DF+FS)^{2}-ES^{2}$, давая ${\frac {\left(PF^{2}-ES^{2}\right)DF^{2}}{PF^{2}}}+2\cdot FS\cdot DF+FS^{2}-ES^{2}=0$. Решая квадратичное уравнение для DF, в пределе, когда ES приближается к FS, меньший корень $DF=ES-FS$. Проще говоря, когда DF приближается к нулю, в пределе $DF^{2}$ термин можно игнорировать: $2\cdot FS\cdot DF+FS^{2}-ES^{2}=0$ приводящие к тому же результату. Очевидно, что df имеет тот же предел, что подтверждает утверждение Ньютона.

Сравнивая силу со стороны кольца HI, вращающегося вокруг PS, с кольцом hi вокруг pS, отношение этих двух сил равно ${\textstyle {\frac {d^{2}}{D^{2}}}}$.

Разделив дуги AT и Bt на соответствующие бесконечно малые кольца, следует, что отношение силы, действующей на дугу AT, вращающуюся вокруг PS, к силе, действующей на дугу AT, вращающуюся вокруг pS, находится в одном и том же отношении, и аналогично отношение сил из-за дуги TB к дуге tA оба вращаются в одинаковом соотношении.

Следовательно, сила, действующая на частицу на любом расстоянии D от центра полой сферы, обратно пропорциональна $D^{2}$, что и доказывает предложение.

Теорема оболочки в

Аналог теоремы о оболочках существует в общей теории относительности (ОТО).

Сферическая симметрия подразумевает, что метрика имеет независимую от времени геометрию Шварцшильда, даже если центральная масса испытывает гравитационный коллапс (Миснер и др., 1973; см. теорему Биркгофа ). имеет Таким образом , метрика вид

$ds^{2}=-(1-2M/r)\,dt^{2}+(1-2M/r)^{-1}\,dr^{2}+r^{2}\,d\Omega ^{2}$

(с использованием геометрических единиц , где $G=c=1$). Для $r>R>0$ (где $R$ — радиус некоторой массовой оболочки), масса действует как дельта-функция в начале координат. Для $r<R$, оболочки массы могут существовать снаружи, но для того, чтобы метрика была неособой в начале координат, $M$ должно быть равно нулю в метрике. Это сводит метрику к плоскому пространству Минковского ; таким образом, внешние оболочки не оказывают гравитационного воздействия.

Этот результат проливает свет на гравитационный коллапс, ведущий к образованию черной дыры, и его влияние на движение световых лучей и частиц снаружи и внутри горизонта событий (Hartle 2003, глава 12).

См. также

• Теорема Часла (гравитация)
• Высота шкалы