Классическая механика

Учебники см. в разделах «Классическая механика» (Гольдштейн) и «Классическая механика» (Киббл и Беркшир) .

Схема орбитального движения спутника вокруг Земли, показывающая перпендикулярные векторы скорости и ускорения (силы), представленные в классической интерпретации.

Классическая механика – это физическая теория, описывающая движение таких объектов, как снаряды , части механизмов , космические корабли , планеты , звезды и галактики . Развитие классической механики повлекло за собой существенные изменения в методах и философии физики. Квалификатор классическая отличает этот тип механики от физики, разработанной после революций в физике начала 20 века , которые выявили ограничения классической механики.

Самая ранняя формулировка классической механики часто называется механикой Ньютона . Он состоит из физических концепций, основанных на основополагающих работах сэра Исаака Ньютона 17 века , и математических методов, изобретенных Готфридом Вильгельмом Лейбницем , Леонардом Эйлером и другими для описания движения тел под действием сил . Позже методы, основанные на энергии, были разработаны Эйлером, Жозефом-Луи Лагранжем , Уильямом Роуэном Гамильтоном и другими, что привело к развитию аналитической механики (которая включает лагранжеву механику и гамильтонову механику ). Эти достижения, достигнутые преимущественно в XVIII и XIX веках, вышли за рамки более ранних работ; они, с некоторыми модификациями, используются во всех областях современной физики.

Если известно нынешнее состояние объекта, подчиняющегося законам классической механики, можно определить, как он будет двигаться в будущем и как он двигался в прошлом. Теория хаоса показывает, что долгосрочные предсказания классической механики ненадежны. Классическая механика дает точные результаты при изучении объектов, не являющихся чрезвычайно массивными и имеющих скорости, не приближающиеся к скорости света . С объектами размером с диаметр атома становится необходимым использовать квантовую механику . Для описания скоростей, приближающихся к скорости света, специальная теория относительности необходима . В тех случаях, когда объекты становятся чрезвычайно массивными, общая теория относительности становится применимой . Некоторые современные источники включают релятивистскую механику в классическую физику как представляющую эту область в ее наиболее развитой и точной форме.

Филиалы

Традиционное деление

Классическая механика традиционно делилась на три основных раздела. Статика — это раздел классической механики, который занимается анализом силы и крутящего момента, действующих на физическую систему, которая не испытывает ускорения, а находится в равновесии с окружающей средой. Кинематика описывает движение точек, тел (объектов) и систем тел (групп объектов) без учета сил , вызывающих их движение. Кинематику как область исследования часто называют «геометрией движения» и иногда рассматривают как раздел математики . Динамика выходит за рамки простого описания поведения объектов и также рассматривает силы, которые его объясняют.Некоторые авторы (например, Тейлор (2005) и Гринвуд (1997) ) включают специальную теорию относительности в классическую динамику.

Силы

Другое деление основано на выборе математического формализма. Классическую механику можно математически представить множеством различных способов. Физическое содержание этих разных формулировок одинаково, но они дают разную информацию и облегчают различные типы вычислений. Хотя термин «ньютоновская механика» иногда используется как синоним нерелятивистской классической физики, он также может относиться к определенному формализму, основанному на законах движения Ньютона . Механика Ньютона в этом смысле подчеркивает силу как векторную величину.

Напротив, аналитическая механика использует скалярные свойства движения, представляющие систему в целом — обычно ее кинетическую энергию и потенциальную энергию . Уравнения движения скаляра выводятся из скалярной величины с помощью некоторого основного принципа изменения . Двумя доминирующими разделами аналитической механики являются лагранжева механика , использующая обобщенные координаты и соответствующие им обобщенные скорости в конфигурационном пространстве , и гамильтонова механика , использующая координаты и соответствующие импульсы в фазовом пространстве . Обе формулировки эквивалентны преобразованию Лежандра для обобщенных координат, скоростей и импульсов; следовательно, оба содержат одну и ту же информацию для описания динамики системы. Существуют и другие формулировки, такие как теория Гамильтона-Якоби , механика Рута и уравнение движения Аппелла . Все уравнения движения частиц и полей в любом формализме могут быть получены из широко применимого результата, называемого принципом наименьшего действия. . Одним из результатов является теорема Нётер , утверждение, которое связывает законы сохранения с соответствующими им симметриями .

По региону применения

Альтернативно разделение может быть произведено по регионам применения:

• Небесная механика , касающаяся звезд , планет и других небесных тел.
• Механика сплошной среды — для материалов, моделируемых как сплошная среда, например, твердых тел и жидкостей (т. е. жидкостей и газов ).
• Релятивистская механика (т.е. включая специальную и общую теории относительности) для тел, скорость которых близка к скорости света.
• Статистическая механика , которая обеспечивает основу для связи микроскопических свойств отдельных атомов и молекул с макроскопическими или объемными термодинамическими свойствами материалов.

Описание объектов и их движения

Анализ движения снаряда является частью классической механики.

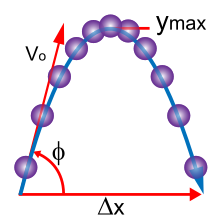
Для простоты классическая механика часто моделирует объекты реального мира как точечные частицы , то есть объекты незначительного размера. Движение точечной частицы определяется небольшим количеством параметров : ее положением, массой и силами приложенными к ней . Классическая механика описывает и более сложные движения протяженных неточечных объектов. Законы Эйлера расширяют законы Ньютона в этой области. Понятия углового момента основаны на том же исчислении, которое используется для описания одномерного движения. Уравнение ракеты расширяет понятие скорости изменения импульса объекта, включив в него эффекты «потери массы» объекта. (Эти обобщения/расширения получены из законов Ньютона, скажем, путем разложения твердого тела на набор точек.)

В действительности объекты, которые может описать классическая механика, всегда имеют ненулевой размер. (Поведение очень маленьких частиц, таких как электрон , более точно описывается квантовой механикой .) Объекты с ненулевым размером имеют более сложное поведение, чем гипотетические точечные частицы, из-за дополнительных степеней свободы , например, бейсбольный мяч может вращаться во время движения. Однако результаты для точечных частиц можно использовать для изучения таких объектов, рассматривая их как составные объекты, состоящие из большого количества коллективно действующих точечных частиц. Центр масс составного объекта ведет себя как точечная частица.

Классическая механика предполагает, что материя и энергия имеют определенные, познаваемые свойства, такие как местоположение в пространстве и скорость. Нерелятивистская механика также предполагает, что силы действуют мгновенно (см. также Действие на расстоянии ).

Кинематика

Основная статья: Кинематика

Производное от SI . «механическое»
(то есть не электромагнитный или тепловой )
единицы измерения кг, м и с

позиция	м
угловое положение/ угол	безразмерный (радиан)
скорость	РС −1
угловая скорость	с −1
ускорение	РС −2
угловое ускорение	с −2
придурок	РС −3
"угловой рывок"	с −3
удельная энергия	м 2 ·с −2
мощность поглощенной дозы	м 2 ·с −3
момент инерции	кг·м 2
импульс	кг·м·с −1
угловой момент	кг·м 2 ·с −1
сила	кг·м·с −2
крутящий момент	кг·м 2 ·с −2
энергия	кг·м 2 ·с −2
власть	кг·м 2 ·с −3
давление и плотность энергии	кг·м −1 ·с −2
поверхностное натяжение	кг·с −2
пружинная константа	кг·с −2
излучение и поток энергии	кг·с −3
кинематическая вязкость	м 2 ·с −1
динамическая вязкость	кг·м −1 ·с −1
плотность (массовая плотность)	кг·м −3
удельный вес (плотность веса)	кг·м −2 ·с −2
плотность чисел	м −3
действие	кг·м 2 ·с −1

Положение называемой точечной частицы определяется относительно системы координат с центром в произвольной фиксированной точке отсчета в пространстве, началом O. координат Простая система координат могла бы описывать положение частицы P с помощью вектора, обозначенного стрелкой с надписью r, указывает от начала координат O до точки P. которая В общем, точечная частица не обязательно должна быть стационарной O. относительно В тех случаях, когда относительно O , r определяется как функция времени . движется P В доэйнштейновской теории относительности (известной как теория относительности Галилея ) время считается абсолютным, т. е. временной интервал , который, по наблюдениям, проходит между любой данной парой событий, одинаков для всех наблюдателей. не только опирается на абсолютное время Классическая механика , но и предполагает евклидову геометрию структуры пространства.

Скорость и скорость

Основные статьи: Скорость и скорость

Скорость смещения во или скорость изменения времени определяется как производная положения по времени:

$\mathbf {v} ={\mathrm {d} \mathbf {r} \over \mathrm {d} t}\,\!$.

В классической механике скорости непосредственно складывают и вычитают. Например, если одна машина движется на восток со скоростью 60 км/ч и обгоняет другую машину, движущуюся в том же направлении со скоростью 50 км/ч, более медленная машина воспринимает более быструю машину как движущуюся на восток со скоростью 60 - 50 = 10 км/ч . Однако с точки зрения более быстрой машины более медленная машина движется на запад со скоростью 10 км/ч, что часто обозначается как -10 км/ч, где знак означает противоположное направление. Скорости являются непосредственно аддитивными как векторные величины ; их необходимо решать с помощью векторного анализа .

объекта в предыдущем обсуждении обозначается вектором u = ud , а скорость второго объекта — вектором v = ve Математически, если скорость первого , где u — скорость первого объекта, v — это скорость второго объекта, а d и e — единичные векторы в направлениях движения каждого объекта соответственно, тогда скорость первого объекта, видимая вторым объектом, равна:

$\mathbf {u} '=\mathbf {u} -\mathbf {v} \,.$

Аналогично, первый объект видит скорость второго объекта как:

$\mathbf {v'} =\mathbf {v} -\mathbf {u} \,.$

Когда оба объекта движутся в одном направлении, это уравнение можно упростить до:

$\mathbf {u} '=(u-v)\mathbf {d} \,.$

Или, игнорируя направление, разницу можно выразить только в скорости:

$u'=u-v\,.$

Ускорение

Основная статья: Ускорение

Ускорение производной , или скорость изменения скорости, является скорости по времени ( вторая производная положения по времени):

$\mathbf {a} ={\mathrm {d} \mathbf {v} \over \mathrm {d} t}={\mathrm {d^{2}} \mathbf {r} \over \mathrm {d} t^{2}}.$

Ускорение представляет собой изменение скорости с течением времени. Скорость может меняться по величине, направлению или по тому и другому. Иногда уменьшение величины скорости « v » называют замедлением , но обычно любое изменение скорости с течением времени, включая замедление, называют ускорением.

Системы отсчета

Основные статьи: Инерциальная система отсчета и преобразование Галилея

Хотя положение, скорость и ускорение частицы могут быть описаны относительно любого наблюдателя в любом состоянии движения, классическая механика предполагает существование особого семейства систем отсчета , в которых механические законы природы принимают сравнительно простую форму. Эти специальные системы отсчета называются инерциальными . Инерциальная система отсчета — это идеализированная система отсчета, в которой объект с нулевой результирующей силой, действующей на него, движется с постоянной скоростью; то есть он либо покоится, либо движется равномерно и прямолинейно. В инерциальной системе отсчета закон движения Ньютона: $F=ma$, действителен.

Неинерциальные системы отсчета ускоряются относительно другой инерциальной системы отсчета. Тело, вращающееся относительно инерциальной системы отсчета, не является инерциальной системой отсчета. Если смотреть из инерциальной системы отсчета, частицы в неинерциальной системе отсчета кажутся движущимися способами, не объясняемыми силами существующих полей в системе отсчета. Следовательно, оказывается, что существуют и другие силы, которые входят в уравнения движения исключительно в результате относительного ускорения. Эти силы называются фиктивными силами , силами инерции или псевдосилами.

Рассмотрим две системы отсчета S и S' . Для наблюдателей в каждой из систем отсчета событие имеет пространственно-временные координаты ( x , y , z , t ) в системе отсчета S и ( x' , y' , z' , t' ) в системе координат S' . Предполагая, что время измеряется одинаково во всех системах отсчета, если мы требуем x = x', когда t = 0 , тогда соотношение между пространственно-временными координатами одного и того же события, наблюдаемого из систем отсчета S' и S , которые движутся со скоростью относительная скорость u в направлении x равна:

${\begin{aligned}x'&=x-tu,\\y'&=y,\\z'&=z,\\t'&=t.\end{aligned}}$

Этот набор формул определяет групповое преобразование, известное как преобразование Галилея (неформально преобразование Галилея ). Эта группа представляет собой предельный случай группы Пуанкаре, используемой в специальной теории относительности . Предельный случай применяется, когда скорость u очень мала по сравнению со c скоростью света .

Преобразования имеют следующие последствия:

• v ′ = v − u (скорость v ′ частицы с точки зрения S ′ медленнее на u, чем ее скорость v с точки зрения S )
• a ′ = a (ускорение частицы одинаково в любой инерциальной системе отсчета)
• F ′ = F (сила, действующая на частицу, одинакова в любой инерциальной системе отсчета)
• Скорость света не является константой в классической механике, а особое положение, отведенное скорости света в релятивистской механике, не имеет аналога в классической механике.

Для некоторых задач удобно использовать вращающиеся координаты (системы отсчета). Тем самым можно либо сохранить отображение в удобную инерциальную систему отсчета, либо ввести дополнительно фиктивную центробежную силу и силу Кориолиса .

Механика Ньютона

Основные статьи: Сила и законы движения Ньютона

Сила в физике — это любое действие, вызывающее изменение скорости объекта; то есть ускориться. Сила возникает внутри поля , например, электростатического поля (вызванного статическими электрическими зарядами), электромагнитного поля (вызванного движущимися зарядами) или гравитационного поля (вызванного массой) и других.

Ньютон был первым, кто математически выразил связь между силой и импульсом . Некоторые физики интерпретируют второй закон движения Ньютона как определение силы и массы, другие считают его фундаментальным постулатом, законом природы. Любая интерпретация имеет одни и те же математические последствия, исторически известные как «Второй закон Ньютона»:

$\mathbf {F} ={\mathrm {d} \mathbf {p} \over \mathrm {d} t}={\mathrm {d} (m\mathbf {v} ) \over \mathrm {d} t}.$

Величина m v называется ( каноническим ) импульсом . Таким образом, результирующая сила, действующая на частицу, равна скорости изменения импульса частицы во времени. Поскольку определение ускорения есть a = d v /d t , второй закон можно записать в упрощенном и более привычном виде:

$\mathbf {F} =m\mathbf {a} \,.$

Пока известна сила, действующая на частицу, второго закона Ньютона достаточно, чтобы описать движение частицы. Как только станут известны независимые соотношения для каждой силы, действующей на частицу, их можно подставить во второй закон Ньютона, чтобы получить обыкновенное дифференциальное уравнение , которое называется уравнением движения .

В качестве примера предположим, что трение является единственной силой, действующей на частицу, и что его можно смоделировать как функцию скорости частицы, например:

$\mathbf {F} _{\rm {R}}=-\lambda \mathbf {v} \,,$

где λ — положительная константа, отрицательный знак означает, что сила противоположна направлению скорости. Тогда уравнение движения будет

$-\lambda \mathbf {v} =m\mathbf {a} =m{\mathrm {d} \mathbf {v} \over \mathrm {d} t}\,.$

Это можно интегрировать, чтобы получить

$\mathbf {v} =\mathbf {v} _{0}e^{{-\lambda t}/{m}}$

где v ₀ — начальная скорость. Это означает, что скорость этой частицы экспоненциально убывает до нуля с течением времени. В этом случае эквивалентной точкой зрения является то, что кинетическая энергия частицы поглощается трением (которое преобразует ее в тепловую энергию в соответствии с законом сохранения энергии ), и частица замедляется. Это выражение можно дополнительно проинтегрировать, чтобы получить положение r частицы как функцию времени.

Важные силы включают гравитационную силу и силу Лоренца для электромагнетизма . Кроме того, третий закон Ньютона иногда можно использовать для вывода сил, действующих на частицу: если известно, что частица A оказывает силу F на другую частицу B , из этого следует, что B должна оказывать равную и противоположную силу реакции , − F на А. , Сильная форма третьего закона Ньютона требует, чтобы F и − F действовали вдоль линии, соединяющей A и B , а слабая форма этого не делает. Для магнитных сил часто встречаются иллюстрации слабой формы третьего закона Ньютона.

Работа и энергия

Основные статьи: Работа (физика) , кинетическая энергия и потенциальная энергия.

постоянная сила F , приложена Если к частице, совершающей смещение Δr , работа , совершаемая силой, определяется как скалярное произведение векторов силы и перемещения:

$W=\mathbf {F} \cdot \Delta \mathbf {r} \,.$

В более общем смысле, если сила изменяется в зависимости от положения по мере движения частицы от r ₁ до r ₂ по пути C , работа, совершаемая частицей, определяется линейным интегралом

$W=\int _{C}\mathbf {F} (\mathbf {r} )\cdot \mathrm {d} \mathbf {r} \,.$

Если работа, совершаемая при перемещении частицы из r ₁ в r _2, одинакова независимо от выбранного пути, то сила называется консервативной . Гравитация является консервативной силой, как и сила идеализированной пружины , определяемая законом Гука . Сила трения неконсервативна.

Кинетическая энергия E _k частицы массы m, движущейся со скоростью v, определяется выражением

$E_{\mathrm {k} }={\tfrac {1}{2}}mv^{2}\,.$

Для протяженных объектов, состоящих из множества частиц, кинетическая энергия составного тела представляет собой сумму кинетических энергий частиц.

Теорема о работе-энергии утверждает, что для частицы постоянной массы m полная работа W, совершаемая частицей при ее движении из положения r ₁ в положение r _2, равна изменению кинетической энергии E _k частицы:

$W=\Delta E_{\mathrm {k} }=E_{\mathrm {k_{2}} }-E_{\mathrm {k_{1}} }={\tfrac {1}{2}}m\left(v_{2}^{\,2}-v_{1}^{\,2}\right).$

Консервативные силы можно выразить как градиент скалярной функции, известной как потенциальная энергия и обозначаемой E _p :

$\mathbf {F} =-\mathbf {\nabla } E_{\mathrm {p} }\,.$

Если все силы, действующие на частицу, консервативны, а Ер _— полная потенциальная энергия (которая определяется как работа причастных сил по перестановке взаимных положений тел), полученная суммированием потенциальных энергий, соответствующих каждой силе

$\mathbf {F} \cdot \Delta \mathbf {r} =-\mathbf {\nabla } E_{\mathrm {p} }\cdot \Delta \mathbf {r} =-\Delta E_{\mathrm {p} }\,.$

Уменьшение потенциальной энергии равно увеличению кинетической энергии

$-\Delta E_{\mathrm {p} }=\Delta E_{\mathrm {k} }\Rightarrow \Delta (E_{\mathrm {k} }+E_{\mathrm {p} })=0\,.$

Этот результат известен как сохранение энергии что полная энергия и гласит ,

$\sum E=E_{\mathrm {k} }+E_{\mathrm {p} }\,,$

является постоянным во времени. Это часто бывает полезно, поскольку многие часто встречающиеся силы являются консервативными.

Лагранжева механика

Основная статья: Лагранжева механика

Лагранжева механика — это формулировка классической механики, основанная на принципе стационарного действия (также известном как принцип наименьшего действия). Его представил итало-французский математик и астроном Жозеф-Луи Лагранж в своей презентации Туринской академии наук в 1760 году. кульминацией которого стал его великий опус 1788 года «Аналитическая механика» . Лагранжева механика описывает механическую систему как пару ${\textstyle (M,L)}$ состоящее из конфигурационного пространства ${\textstyle M}$ и плавная функция ${\textstyle L}$ внутри этого пространства, называемого лагранжианом. Для многих систем ${\textstyle L=T-V,}$ где ${\textstyle T}$ и $V$ – кинетическая и потенциальная энергия системы соответственно. Принцип стационарного действия требует, чтобы функционал действия системы был получен из ${\textstyle L}$ должна оставаться в стационарной точке ( максимум , минимум или седло ) на протяжении всей временной эволюции системы. Это ограничение позволяет рассчитывать уравнения движения системы с использованием уравнений Лагранжа.

Гамильтонова механика

Основная статья: гамильтонова механика

Гамильтонова механика возникла в 1833 как переформулировка механики Лагранжа . Представлено сэром Уильямом Роуэном Гамильтоном . Гамильтонова механика заменяет (обобщенные) скорости. ${\dot {q}}^{i}$ используется в лагранжевой механике с (обобщенными) импульсами . Обе теории дают интерпретации классической механики и описывают одни и те же физические явления. Гамильтонова механика имеет тесную связь с геометрией (в частности, симплектической геометрией и пуассоновскими структурами ) и служит связующим звеном между классической и квантовой механикой .

В этом формализме динамика системы определяется уравнениями Гамильтона, которые выражают производные по времени переменных положения и импульса через частные производные функции, называемой гамильтонианом:

$${\frac {\mathrm {d} {\boldsymbol {q}}}{\mathrm {d} t}}={\frac {\partial {\mathcal {H}}}{\partial {\boldsymbol {p}}}},\quad {\frac {\mathrm {d} {\boldsymbol {p}}}{\mathrm {d} t}}=-{\frac {\partial {\mathcal {H}}}{\partial {\boldsymbol {q}}}}.$$

Гамильтониан представляет собой преобразование Лежандра лагранжиана и во многих ситуациях, представляющих физический интерес, равен полной энергии системы.

Границы действия

Область применимости классической механики

Многие разделы классической механики представляют собой упрощения или приближения более точных форм; Двумя наиболее точными из них являются общая теория относительности и релятивистская статистическая механика . Геометрическая оптика является приближением к квантовой теории света и не имеет превосходящей «классической» формы.

Когда и квантовая механика, и классическая механика не могут применяться, например, на квантовом уровне со многими степенями свободы, квантовая теория поля используется (КТП). КТП имеет дело с малыми расстояниями и большими скоростями со многими степенями свободы, а также с возможностью любого изменения количества частиц в ходе взаимодействия. При рассмотрении больших степеней свободы на макроскопическом уровне статистическая механика становится полезной . Статистическая механика описывает поведение большого (но счетного) числа частиц и их взаимодействия в целом на макроскопическом уровне. Статистическая механика в основном используется в термодинамике для систем, выходящих за рамки положений классической термодинамики. В случае объектов с высокой скоростью , приближающейся к скорости света, классическая механика усиливается специальной теорией относительности . В случае, если объекты становятся чрезвычайно тяжелыми (т.е. их радиус Шварцшильда не является пренебрежимо малым для данного применения), отклонения от Ньютоновская механика становится очевидной и может быть выражена количественно с помощью параметризованного постньютоновского формализма . В этом случае общая теория относительности становится применимой (ОТО). Однако до сих пор не существует теории квантовой гравитации, объединяющей ОТО и КТП в том смысле, что ее можно было бы использовать, когда объекты становятся чрезвычайно маленькими и тяжелыми. ^{[4] [5]}

Ньютоновское приближение

В специальной теории относительности импульс частицы определяется выражением

$\mathbf {p} ={\frac {m\mathbf {v} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,,$

где m — масса покоя частицы, v — ее скорость, v — модуль v , а c — скорость света.

Если v очень мало по сравнению с c , v ² / с ² примерно равно нулю, и поэтому

$\mathbf {p} \approx m\mathbf {v} \,.$

Таким образом, уравнение Ньютона p = m v является аппроксимацией релятивистского уравнения для тел, движущихся со скоростью, малой по сравнению со скоростью света.

Например, релятивистская циклотронная частота циклотрона , гиротрона или магнетрона высокого напряжения определяется выражением

$f=f_{\mathrm {c} }{\frac {m_{0}}{m_{0}+{\frac {T}{c^{2}}}}}\,,$

где f _c — классическая частота электрона (или другой заряженной частицы) с кинетической энергией T и покоя массой m ₀ , вращающейся в магнитном поле. Масса (покоя) электрона равна 511 кэВ. Таким образом, частотная коррекция составляет 1% для магнитной вакуумной лампы с ускоряющим напряжением постоянного тока 5,11 кВ.

Классическое приближение квантовой механики

Лучевое приближение классической механики не работает, когда длина волны де Бройля ненамного меньше других размеров системы. Для нерелятивистских частиц эта длина волны равна

$\lambda ={\frac {h}{p}}$

где h — постоянная Планка , а p — импульс.

Опять же, это происходит с электронами раньше, чем с более тяжелыми частицами. Например, электроны, использованные Клинтоном Дэвиссоном и Лестером Гермером в 1927 году, ускоренные напряжением 54 В, имели длину волны 0,167 нм, что было достаточно для того, чтобы возникал один дифракционный боковой лепесток при отражении от грани кристалла никеля с расстоянием между атомами . 0,215 нм. С вакуумной камерой большего размера казалось бы относительно легко увеличить угловое разрешение примерно с радиана до миллирадиана и увидеть квантовую дифракцию на периодических картинах компьютерной памяти интегральной схемы .

Более практические примеры провала классической механики в инженерном масштабе — это проводимость посредством квантового туннелирования в туннельных диодах и очень узких транзисторов затворах в интегральных схемах .

Классическая механика представляет собой такое же предельно высокочастотное приближение, как и геометрическая оптика . Чаще всего оно точнее, поскольку описывает частицы и тела с массой покоя . Они имеют больший импульс и, следовательно, более короткие длины волн де Бройля, чем безмассовые частицы, такие как свет, с той же кинетической энергией.

История

Основная статья: История классической механики

Хронологическое руководство см. в разделе «Хронология классической механики» .

Изучение движения тел является древним, что делает классическую механику одним из старейших и крупнейших предметов науки , техники и технологий . Развитие классической механики привело к развитию многих областей математики.

Некоторые греческие философы древности, в том числе Аристотель , основатель аристотелевской физики , возможно, были первыми, кто придерживался идеи, что «все происходит по какой-то причине» и что теоретические принципы могут помочь в понимании природы. Хотя современному читателю многие из этих сохранившихся идей кажутся в высшей степени разумными, здесь явно отсутствует как математическая теория , так и контролируемый эксперимент в том виде, в котором мы их знаем. Позже они стали решающими факторами в формировании современной науки, а их раннее применение стало известно как классическая механика. В своей книге «Элемента супер демонстрации» ponderum средневековый математик Йордан де Немор представил концепцию «позиционной гравитации » и использования составляющих сил .

Трехступенчатая теория импульса по Альберту Саксонскому.

Первым опубликованным причинно-следственным объяснением движения планет Иоганна Кеплера была «Новая астрономия» , опубликованная в 1609 году. На основании наблюдений Тихо Браге за орбитой Марса он пришел к выводу , что орбиты планет представляют собой эллипсы . Этот разрыв с античной мыслью произошел примерно в то же время, когда Галилей предлагал абстрактные математические законы движения объектов. Возможно, он провел (а может и нет) знаменитый эксперимент по сбрасыванию двух пушечных ядер разного веса с Пизанской башни , показав, что они оба упали на землю одновременно. Реальность этого конкретного эксперимента оспаривается, но он действительно проводил количественные эксперименты, катая шарики по наклонной плоскости . Его теория ускоренного движения была выведена из результатов таких экспериментов и составляет краеугольный камень классической механики. В 1673 году Христиан Гюйгенс описал в своей работе «Horologium Oscillatorium» первые два закона движения . Эта работа также является первым современным трактатом, в котором физическая проблема ( ускоренное движение падающего тела) идеализируется с помощью набора параметров, а затем математически анализируется, и представляет собой одну из плодотворных работ прикладной математики .

Сэр Исаак Ньютон (1643–1727), влиятельная фигура в истории физики, чьи три закона движения составляют основу классической механики.

Ньютон основал свои принципы натурфилософии на трех предложенных законах движения : законе инерции , своем втором законе ускорения (упомянутом выше) и законе действия и противодействия ; и, следовательно, заложил основы классической механики. И второй, и третий законы Ньютона получили должное научное и математическое толкование в «Philosophiæ Naturalis Principia Mathematica» Ньютона . В этом они отличаются от более ранних попыток объяснения подобных явлений, которые были либо неполными, неверными или имели мало точного математического выражения. Ньютон также сформулировал принципы сохранения импульса и момента импульса . В механике Ньютон был также первым, кто дал первую правильную научную и математическую формулировку гравитации в законе всемирного тяготения Ньютона . Сочетание законов движения Ньютона и гравитации дает наиболее полное и точное описание классической механики. Он продемонстрировал, что эти законы применимы как к повседневным объектам, так и к небесным объектам. В частности, он получил теоретическое объяснение Кеплера Законы движения планет .

Ньютон ранее изобрел исчисление ; однако «Начала» были сформулированы полностью на основе давно устоявшихся геометрических методов, подражающих Евклиду . Ньютон и большинство его современников, за исключением Гюйгенса , исходили из предположения, что классическая механика сможет объяснить все явления, включая свет , в форме геометрической оптики . Даже при открытии так называемых колец Ньютона ( явление интерференции волн ) он придерживался собственной корпускулярной теории света .

Вкладом Лагранжа была реализация идей Ньютона на языке современной математики, называемой теперь лагранжевой механикой .

После Ньютона классическая механика стала основной областью исследований как в математике, так и в физике. Математические формулировки постепенно позволяли находить решения гораздо большему числу проблем. Первая заметная математическая обработка была сделана в 1788 году Жозефом Луи Лагранжем . Лагранжева механика, в свою очередь, была переформулирована в 1833 году Уильямом Роуэном Гамильтоном .

Гамильтон разработал альтернативу лагранжевой механике, которая теперь называется гамильтоновой механикой .

В конце XIX века были обнаружены некоторые трудности, которые могла решить только более современная физика. Некоторые из этих трудностей были связаны с совместимостью с теорией электромагнетизма и знаменитым экспериментом Майкельсона-Морли . Решение этих проблем привело к созданию специальной теории относительности , которую часто до сих пор считают частью классической механики.

Второй набор трудностей был связан с термодинамикой. В сочетании с термодинамикой классическая механика приводит к парадоксу Гиббса классической статистической механики , в котором энтропия не является четко определенной величиной. Излучение черного тела не было объяснено без введения квантов . Когда эксперименты достигли атомного уровня, классическая механика не смогла объяснить, даже приблизительно, такие базовые вещи, как энергетические уровни и размеры атомов и фотоэлектрический эффект . Усилия по решению этих проблем привели к развитию квантовой механики .

С конца XX века классическая механика в физике уже не является самостоятельной теорией. Вместо этого классическая механика теперь считается приближенной теорией к более общей квантовой механике. Акцент сместился на понимание фундаментальных сил природы, таких как Стандартная модель и ее более современные расширения в единую теорию всего . Классическая механика — это теория, полезная для изучения движения неквантово-механических частиц низкой энергии в слабых гравитационных полях.

См. также

• Динамическая система
• Список уравнений классической механики
• Список публикаций по классической механике
• Список учебников по классической механике и квантовой механике
• Молекулярная динамика
• Законы движения Ньютона
• Специальная теория относительности
• Квантовая механика
• Квантовая теория поля

Дальнейшее чтение

• Алонсо, М.; Финн, Дж. (1992). Фундаментальная университетская физика . Аддисон-Уэсли.
• Фейнман, Ричард (1999). Фейнмановские лекции по физике . Издательство Персей. ISBN  978-0-7382-0092-7 .
• Фейнман, Ричард; Филлипс, Ричард (1998). Шесть простых пьес . Издательство Персей. ISBN  978-0-201-32841-7 .
• Гольдштейн, Герберт ; Чарльз П. Пул; Джон Л. Сафко (2002). Классическая механика (3-е изд.). Эддисон Уэсли. ISBN  978-0-201-65702-9 .
• Киббл, Том ВБ ; Беркшир, Фрэнк Х. (2004). Классическая механика (5-е изд.) . Издательство Имперского колледжа . ISBN  978-1-86094-424-6 .
• Клеппнер, Д.; Коленков, Р.Дж. (1973). Введение в механику . МакГроу-Хилл. ISBN  978-0-07-035048-9 .
• Ландау, Л.Д.; Лифшиц, Э.М. (1972). Курс теоретической физики, Том. 1 – Механика . Книжная компания Франклина. ISBN  978-0-08-016739-8 .
• Морен, Дэвид (2008). Введение в классическую механику: с проблемами и решениями (1-е изд.). Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-87622-3 .
• Джеральд Джей Сассман ; Джек Уиздом (2001). Структура и интерпретация классической механики . МТИ Пресс. ISBN  978-0-262-19455-6 .
• О'Доннелл, Питер Дж. (2015). Существенная динамика и относительность . ЦРК Пресс. ISBN  978-1-4665-8839-4 .
• Торнтон, Стивен Т.; Мэрион, Джерри Б. (2003). Классическая динамика частиц и систем (5-е изд.) . Брукс Коул. ISBN  978-0-534-40896-1 .

Внешние ссылки

• Кроуэлл, Бенджамин. Свет и материя (вводный текст, использует алгебру с дополнительными разделами, связанными с исчислением)
• Фитцпатрик, Ричард. Классическая механика (использует исчисление)
• Хойланд, Пол (2004). Предпочтительные системы отсчета и теория относительности
• Хорбач, Марко, « Конспекты курса классической механики ».
• Рошу, Харет К., « Классическая механика ». Физическое образование. 1999. [arxiv.org: физика/9909035]
• Шапиро, Джоэл А. (2003). Классическая механика
• Сассман, Джеральд Джей и Уиздом, Джек и Майер, Мейнхард Э. (2001). Структура и интерпретация классической механики
• Тонг, Дэвид. Классическая динамика (конспекты Кембриджских лекций по лагранжевому и гамильтонову формализму)
• Цифровая библиотека кинематических моделей для проектирования (KMODDL)
  Фильмы и фотографии сотен работающих моделей механических систем в Корнельском университете . Также включает в себя электронную библиотеку классических текстов по машиностроению и проектированию.
• MIT OpenCourseWare 8.01: Классическая механика Бесплатные видеоролики с реальными лекциями курса со ссылками на конспекты лекций, задания и экзамены.
• Алехандро А. Торасса, О классической механике