Статика

Статический анализ в экономике см. в разделе «Сравнительная статика» . Информацию о методе статической коррекции, используемой в разведочной геофизике, см. в разделе «Сейсмология отражений» . Чтобы узнать о других целях, см. Статический анализ .

Не путать со статистикой .

Статика — это раздел классической механики , который занимается анализом силы и крутящего момента, действующих на физическую систему , которая не испытывает ускорения , а находится в равновесии с окружающей средой.

Если ${\textbf {F}}$ – сумма сил, действующих на систему, $m$ - масса системы и ${\textbf {a}}$ является ускорением системы, второй закон Ньютона гласит, что ${\textbf {F}}=m{\textbf {a}}\,$ (жирный шрифт указывает на векторную величину, т.е. величину и направление ). Если ${\textbf {a}}=0$, затем ${\textbf {F}}=0$. Что касается системы, находящейся в статическом равновесии, то ускорение равно нулю, система либо покоится, либо ее центр масс движется с постоянной скоростью .

Применение предположения о нулевом ускорении к суммированию моментов, действующих на систему, приводит к ${\textbf {M}}=I\alpha =0$, где ${\textbf {M}}$ представляет собой сумму всех моментов, действующих на систему, $I$ – момент инерции массы и $\alpha$ – угловое ускорение системы. Для системы, где $\alpha =0$, это также правда, что ${\textbf {M}}=0.$

Вместе уравнения ${\textbf {F}}=m{\textbf {a}}=0$ («первое условие равновесия») и ${\textbf {M}}=I\alpha =0$ («второе условие равновесия») можно использовать для определения неизвестных величин, действующих на систему.

История

Архимед (ок. 287–212 до н. э.) провел новаторскую работу в области статики. Более поздние разработки в области статики можно найти в работах Тебита .

Предыстория

Сила

Сила – это действие одного тела на другое. Сила — это либо толчок, либо притяжение, и она стремится переместить тело в направлении своего действия. Действие силы характеризуется ее величиной, направлением действия и точкой приложения. Таким образом, сила является векторной величиной, поскольку ее действие зависит как от направления, так и от величины действия.

Силы подразделяются на контактные и объемные. Контактная сила создается прямым физическим контактом; Примером может служить сила, действующая на тело со стороны опорной поверхности. Объемная сила генерируется в силу положения тела внутри силового поля, такого как гравитационное, электрическое или магнитное поле, и не зависит от контакта с любым другим телом. Примером объемной силы является вес тела в гравитационном поле Земли.

Момент силы

Помимо стремления переместить тело в направлении приложения, сила может также стремиться повернуть тело вокруг оси. Осью может быть любая линия, которая не пересекается и не параллельна линии действия силы. Эта тенденция вращения известна как момент силы ( M ). Момент также называют крутящим моментом .

Момент о точке

Схема плеча момента силы F.

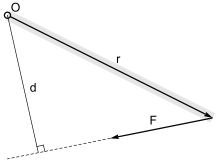
Величина момента силы в точке O равна расстоянию по перпендикуляру от O до линии действия F , умноженному на величину силы: M = F · d , где

F = приложенная сила

d = расстояние по перпендикуляру от оси до линии действия силы. Это перпендикулярное расстояние называется плечом момента.

Направление момента определяется правилом правой руки, при котором движение против часовой стрелки (CCW) выходит за пределы страницы, а по часовой стрелке (CW) — внутрь страницы. Направление момента можно учесть, используя установленное соглашение о знаках, например знак плюс (+) для моментов против часовой стрелки и знак минус (-) для моментов по часовой стрелке или наоборот. Моменты можно суммировать как векторы.

В векторном формате момент можно определить как векторное произведение радиус-вектора r (вектора от точки O до линии действия) и вектора силы F :

${\textbf {M}}_{O}={\textbf {r}}\times {\textbf {F}}$

$r=\left({\begin{array}{cc}x_{00}&...&x_{0j}\\x_{01}&...&x_{1j}\\...&...&...\\x_{i0}&...&x_{ij}\\\end{array}}\right)$

$F=\left({\begin{array}{cc}f_{00}&...&f_{0j}\\f_{01}&...&f_{1j}\\...&...&...\\f_{i0}&...&f_{ij}\\\end{array}}\right)$

Теорема Вариньона

Теорема Вариньона утверждает, что момент силы относительно любой точки равен сумме моментов составляющих силы относительно этой же точки.

равновесия

Статическое равновесие частицы — важное понятие в статике. Частица находится в равновесии только в том случае, если равнодействующая всех сил, действующих на частицу, равна нулю. В прямоугольной системе координат уравнения равновесия могут быть представлены тремя скалярными уравнениями, где суммы сил по всем трем направлениям равны нулю. Инженерным применением этой концепции является определение натяжения до трех тросов под нагрузкой, например, сил , действующих на каждый трос подъемника, поднимающего объект, или растяжек, удерживающих воздушный шар на земле.

Момент инерции

В классической механике момент инерции , также называемый моментом массы, инерцией вращения, полярным моментом инерции массы или угловой массой (единицы СИ кг·м²), является мерой сопротивления объекта изменениям его вращения. Это инерция вращающегося тела по отношению к его вращению. Момент инерции играет во вращательной динамике почти ту же роль, что и масса в линейной динамике, описывая взаимосвязь между угловым моментом и угловой скоростью, крутящим моментом и угловым ускорением, а также некоторыми другими величинами. Символы I и J обычно используются для обозначения момента инерции или полярного момента инерции.

В то время как простая скалярная трактовка момента инерции достаточна для многих ситуаций, более продвинутая тензорная трактовка позволяет анализировать такие сложные системы, как волчки и гироскопическое движение.

Эта концепция была введена Леонардом Эйлером в его книге 1765 года Theoria motus corporum Solidorum seurigidorum ; он обсуждал момент инерции и многие связанные с ним концепции, такие как главная ось инерции.

Приложения

Твердые тела

Статика используется при анализе конструкций, например, в архитектурном и строительном проектировании . Сопротивление материалов — это родственная область механики, которая во многом зависит от применения статического равновесия. Ключевым понятием является центр тяжести покоящегося тела: он представляет собой воображаемую точку, в которой находится вся масса тела . Положение точки относительно оснований , на которых лежит тело, определяет его устойчивость при воздействии внешних сил. Если центр тяжести существует вне фундамента, то тело неустойчиво, поскольку действует крутящий момент: любое небольшое возмущение приведет к падению или опрокидыванию тела. Если центр тяжести находится внутри фундамента, тело устойчиво, поскольку на тело не действует чистый крутящий момент. Если центр тяжести совпадает с основаниями, то тело называют метастабильным .

Жидкости

Гидростатика , также известная как статика жидкости , — это исследование жидкостей в состоянии покоя (т. е. в статическом равновесии). Характеристика любой покоящейся жидкости заключается в том, что сила, действующая на любую частицу жидкости, одинакова во всех точках на одной и той же глубине (или высоте) внутри жидкости. Если результирующая сила больше нуля, жидкость будет двигаться в направлении результирующей силы. Эта концепция была впервые сформулирована в несколько расширенном виде французским математиком и философом Блезом Паскалем в 1647 году и стала известна как закон Паскаля . Он имеет множество важных применений в гидравлике . Архимед , Абу Райхан аль-Бируни , Аль-Хазини и Галилео Галилей также были крупными фигурами в развитии гидростатики.

См. также

• Схема Кремоны
• Динамика
• Твердая механика

Ссылки

• Бир, Ф.П. и Джонстон-младший, ER (1992). Статика и механика материалов . МакГроу-Хилл, Инк.
• Пиво, ФП; Джонстон-младший, скорая помощь; Айзенберг (2009). Векторная механика для инженеров: Статика, 9-е изд . МакГроу Хилл. ISBN  978-0-07-352923-3 .
• Морелон, Режис; Рашед, Рошди, ред. (1996), Энциклопедия истории арабской науки , том. 3, Рутледж, ISBN  978-0415124102