Простое гармоническое движение

В механике и физике , простое гармоническое движение (иногда сокращенно SHM ) — это особый тип периодического движения, которое испытывает объект из-за восстанавливающей силы величина которой прямо пропорциональна расстоянию объекта от положения равновесия и действует в направлении положения равновесия. В результате возникают колебания описываемые синусоидой , которые продолжаются бесконечно (если их не тормозит трение или какое-либо другое рассеяние энергии , ).

Простое гармоническое движение может служить математической моделью для множества движений, но типичным примером является колебание массы на пружине , когда на нее действует линейная упругая восстанавливающая сила, определяемая законом Гука . Движение синусоидальное во времени и демонстрирует единственную резонансную частоту. Другие явления можно смоделировать простым гармоническим движением, включая движение простого маятника , хотя для того, чтобы это была точная модель, результирующая сила , действующая на объект на конце маятника, должна быть пропорциональна смещению (и даже в этом случае это хорошее приближение только тогда, когда угол поворота мал, см. приближение малого угла ). Простое гармоническое движение также можно использовать для моделирования молекулярных колебаний .

Простое гармоническое движение обеспечивает основу для характеристики более сложного периодического движения с помощью методов анализа Фурье .

Введение [ править ]

Движение частицы, движущейся по прямой с ускорением, направление которого всегда направлено к фиксированной точке на прямой и величина которого пропорциональна смещению от неподвижной точки, называется простым гармоническим движением. ^[1]

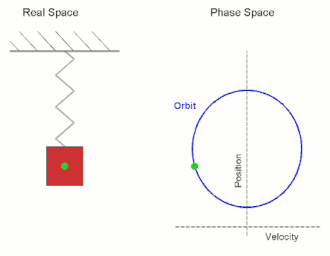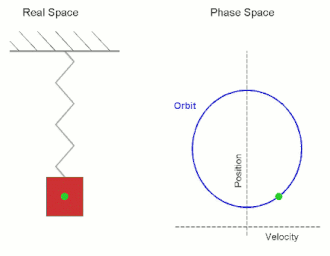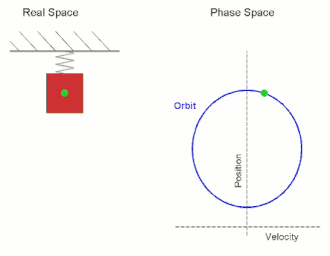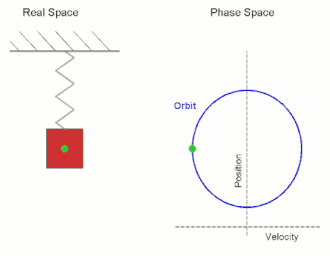
На схеме показан простой гармонический осциллятор , состоящий из груза, прикрепленного к одному концу пружины. Другой конец пружины соединен с жесткой опорой, например стеной. Если система остается в покое в положении равновесия не действует результирующая сила , то на массу . Однако если масса смещается из положения равновесия, пружина оказывает восстанавливающую упругую силу, подчиняющуюся закону Гука .

Математически восстанавливающая сила $F$ определяется выражением

\mathbf {F} =-k\mathbf {x} ,

где

F

— восстанавливающая упругая сила, действующая на пружину (в единицах СИ : Н ),

k

— жесткость пружины ( Н ·м ⁻¹), а

x

– смещение от положения равновесия (м).

Для любого простого механического гармонического генератора:

Когда система смещается из положения равновесия, восстанавливающая сила, подчиняющаяся закону Гука, стремится вернуть систему в равновесие.

Как только масса смещается из положения равновесия, на нее действует чистая восстанавливающая сила. В результате он ускоряется и начинает возвращаться в положение равновесия. Когда масса приближается к положению равновесия, восстанавливающая сила уменьшается. В положении равновесия чистая восстанавливающая сила исчезает. Однако при $x = 0$ масса имеет импульс из-за ускорения, которое сообщила восстанавливающая сила. Следовательно, масса продолжает выходить за положение равновесия, сжимая пружину. Затем чистая восстанавливающая сила замедляет его до тех пор, пока его скорость не достигнет нуля, после чего он снова ускоряется до положения равновесия.

Пока в системе нет потерь энергии , масса продолжает колебаться. Таким образом, простое гармоническое движение является разновидностью периодического движения. Если энергия теряется в системе, то масса демонстрирует затухающие колебания .

Обратите внимание, что если графики реального и фазового пространства не совпадают, движение в фазовом пространстве становится эллиптическим. Ограниченная площадь зависит от амплитуды и максимального импульса.

Динамика [ править ]

В механике Ньютона для одномерного простого гармонического движения уравнение движения, представляющее собой линейное обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами, может быть получено с помощью 2-го закона Ньютона и закона Гука для массы на пружине .

F_{\mathrm {net} }=m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-kx,

где

m

- инерционная масса колеблющегося тела,

x

- его смещение от положения равновесия (или среднего), а

k

- константа ( постоянная пружины для массы на пружине).

Поэтому,

{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-{\frac {k}{m}}x,

Решение приведенного выше дифференциального уравнения дает решение, которое является синусоидальной функцией : $x(t)=c_{1}\cos \left(\omega t\right)+c_{2}\sin \left(\omega t\right),$ где ${\textstyle \omega ={\sqrt {{k}/{m}}}.}$ Смысл констант $c_{1}$ и $c_{2}$ можно легко найти: настройка $t=0$ в приведенном выше уравнении мы видим, что $x(0)=c_{1}$ , так что $c_{1}$ - начальное положение частицы, $c_{1}=x_{0}$ ; взяв производную этого уравнения и приравняв ее к нулю, мы получим, что ${\dot {x}}(0)=\omega c_{2}$ , так что $c_{2}$ - начальная скорость частицы, деленная на угловую частоту, $c_{2}={\frac {v_{0}}{\omega }}$ . Таким образом, мы можем написать:

x(t)=x_{0}\cos \left({\sqrt {\frac {k}{m}}}t\right)+{\frac {v_{0}}{\sqrt {\frac {k}{m}}}}\sin \left({\sqrt {\frac {k}{m}}}t\right).

Это уравнение также можно записать в виде:

x(t)=A\cos \left(\omega t-\varphi \right),

где

$A={\sqrt {{c_{1}}^{2}+{c_{2}}^{2}}}$
$\tan \varphi ={\frac {c_{2}}{c_{1}}},$
$\sin \varphi ={\frac {c_{2}}{A}},\;\cos \varphi ={\frac {c_{1}}{A}}$

или эквивалентно

$A=|c_{1}+c_{2}i|,$
$\varphi =\arg(c_{1}+c_{2}i)$

В решении $c 1$ и $c 2$ представляют собой две константы, определяемые начальными условиями (в частности, начальное положение в момент времени $t = 0$ равно $c 1$ , а начальная скорость равна $c 2 ω$ ), а начало координат установлено как положение равновесия. ^[А] Каждая из этих констант несет физический смысл движения: $А$ — амплитуда (максимальное смещение от положения равновесия), $ω = 2 πf$ — угловая частота , $φ$ — начальная фаза . ^[Б]

Используя методы исчисления , можно найти скорость и ускорение как функцию времени:

v(t)={\frac {\mathrm {d} x}{\mathrm {d} t}}=-A\omega \sin(\omega t-\varphi ),

Скорость: ${\omega }{\sqrt {A^{2}-x^{2}}}$
Максимальная скорость: $v = ωA$ (в точке равновесия)

a(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-A\omega ^{2}\cos(\omega t-\varphi ).

Максимальное ускорение: $Aω 2$ (в крайних точках)

По определению, если масса $m$ находится под действием SHM, ее ускорение прямо пропорционально смещению.

a(x)=-\omega ^{2}x.

где

\omega ^{2}={\frac {k}{m}}

Поскольку $ω = 2 πf$ ,

f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}},

и, поскольку

Т = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1 / f,

где

Т

– период времени,

T=2\pi {\sqrt {\frac {m}{k}}}.

Эти уравнения показывают, что простое гармоническое движение изохронно (период и частота не зависят от амплитуды и начальной фазы движения).

Энергия [ править ]

Подставив $ω 2$ с $k / m$ , кинетическая энергия $K$ системы в момент времени $t$ равна

K(t)={\tfrac {1}{2}}mv^{2}(t)={\tfrac {1}{2}}m\omega ^{2}A^{2}\sin ^{2}(\omega t-\varphi )={\tfrac {1}{2}}kA^{2}\sin ^{2}(\omega t-\varphi ),

а потенциальная энергия

U(t)={\tfrac {1}{2}}kx^{2}(t)={\tfrac {1}{2}}kA^{2}\cos ^{2}(\omega t-\varphi ).

При отсутствии трения и других потерь энергии полная механическая энергия имеет постоянное значение.

E=K+U={\tfrac {1}{2}}kA^{2}.

Примеры [ править ]

Недемпфированная система пружина-масса совершает простое гармоническое движение.

Следующие физические системы являются примерами простого гармонического осциллятора .

Месса на источнике [ править ]

Масса $m,$ прикрепленная к пружине с жесткостью пружины $k,$ демонстрирует простое гармоническое движение в замкнутом пространстве . Уравнение для описания периода

T=2\pi {\sqrt {\frac {m}{k}}}

показывает, что период колебаний не зависит от амплитуды, хотя на практике амплитуда должна быть небольшой. Приведенное выше уравнение справедливо и в том случае, когда к массе прилагается дополнительная постоянная сила, т. е. дополнительная постоянная сила не может изменить период колебаний.

Равномерное круговое движение [ править ]

Простое гармоническое движение можно рассматривать как одномерную проекцию равномерного кругового движения . Если объект движется с угловой скоростью $ω$ по окружности радиуса $r$ с центром в начале плоскости $xy$ , то его движение по каждой координате является простым гармоническим движением с амплитудой $r$ и угловой частотой $ω$ .

Колебательное движение [ править ]

Движение тела, при котором оно движется к определенной точке и обратно, также называется колебательным движением или вибрационным движением. Период времени можно рассчитать по

T=2\pi {\sqrt {\frac {l}{g}}}

где l — расстояние от вращения до центра масс объекта, подвергающегося SHM, а g — постоянная гравитационного поля. Это аналог системы масса-пружина.

Масса простого маятника [ править ]

В малоугловом приближении движение простого маятника аппроксимируется простым гармоническим движением. Период массы, прикрепленной к маятнику длины $l$ с ускорением свободного падения $g$ дается

T=2\pi {\sqrt {\frac {l}{g}}}

Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но не от ускорения свободного падения. $g$ , следовательно, маятник той же длины на Луне будет качаться медленнее из-за более низкой напряженности гравитационного поля Луны. Поскольку значение $g$ незначительно варьируется по поверхности земли, период времени будет незначительно меняться от места к месту, а также будет меняться в зависимости от высоты над уровнем моря.

Это приближение является точным только для малых углов, поскольку выражение для углового ускорения $α$ пропорционально синусу угла смещения:

-mgl\sin \theta =I\alpha ,

где

I

— момент инерции . Когда

θ

мало,

sin θ \approx θ

, и поэтому выражение принимает вид

-mgl\theta =I\alpha

что делает угловое ускорение прямо пропорциональным и противоположным

θ

, удовлетворяя определению простого гармонического движения (эта результирующая сила прямо пропорциональна смещению от среднего положения и направлена к среднему положению).

Коктепер [ править ]

Механизм кулисного механизма можно использовать для преобразования вращательного движения в линейное возвратно-поступательное движение. Линейное движение может принимать различные формы в зависимости от формы паза, но основное ярмо с постоянной скоростью вращения создает линейное движение, имеющее простую гармоническую форму.

См. также [ править ]

Примечания [ править ]

^
Выбор использования косинуса в этом уравнении является соглашением. Другими допустимыми формулировками являются:
$x(t)=A\sin \left(\omega t+\varphi '\right),$ где $\tan \varphi '={\frac {c_{1}}{c_{2}}},$
поскольку $cos θ = sin(π / 2 - θ)$ .
^
Максимальное смещение (то есть амплитуда) $x max$ возникает, когда $cos(ωt \pm φ) = 1$ и, следовательно, $x max = A.$ когда

Ссылки [ править ]

^ «Простое гармоническое движение – понятия» .

Фаулз, Грант Р.; Кэссидей, Джордж Л. (2005). Аналитическая механика (7-е изд.). Томсон Брукс/Коул. ISBN 0-534-49492-7 .
Тейлор, Джон Р. (2005). Классическая механика . Университетские научные книги. ISBN 1-891389-22-Х .
Торнтон, Стивен Т.; Мэрион, Джерри Б. (2003). Классическая динамика частиц и систем (5-е изд.). Брукс Коул. ISBN 0-534-40896-6 .
Уокер, Джерл (2011). Принципы физики (9-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN 978-0-470-56158-4 .

Внешние ссылки [ править ]

[cnote_A] 
Выбор использования косинуса в этом уравнении является соглашением. Другими допустимыми формулировками являются:
$x(t)=A\sin \left(\omega t+\varphi '\right),$ где $\tan \varphi '={\frac {c_{1}}{c_{2}}},$
поскольку $cos θ = sin(π / 2 - θ)$ .

[cnote_B] 
Максимальное смещение (то есть амплитуда) $x max$ возникает, когда $cos(ωt \pm φ) = 1$ и, следовательно, $x max = A.$ когда

[1] «Простое гармоническое движение – понятия» .

[1]

[А]

[Б]