Момент (физика)

Не путать с Импульсом .

Чтобы узнать о математической концепции, см. Момент (математика) . О моменте силы, иногда сокращаемом до «момента», см. Крутящий момент .

В физике момент — это математическое выражение , включающее произведение силы и перпендикулярного расстояния от точки действия силы. Моменты обычно определяются относительно фиксированной точки отсчета и относятся к физическим величинам, расположенным на некотором расстоянии от точки отсчета. Таким образом, момент учитывает местоположение или расположение количества. Например, момент силы, часто называемый крутящим моментом , представляет собой произведение силы, действующей на объект, и расстояния от опорной точки до объекта. В принципе, любую физическую величину можно умножить на расстояние, чтобы получить момент. Обычно используемые величины включают силы, массы и электрического заряда распределение .

Разработка

В своей самой простой форме момент — это произведение расстояния до точки, возведенного в степень, и физической величины. (например, сила или электрический заряд) в этот момент:

$\mu _{n}=r^{n}\,Q,$

где $Q$ - это физическая величина, такая как сила, приложенная в точке, или точечный заряд, или точечная масса и т. д. Если величина не сосредоточена исключительно в одной точке, момент является интегралом плотности этой величины в пространстве:

$\mu _{n}=\int r^{n}\rho (r)\,dr$

где $\rho$ — это распределение плотности заряда, массы или любой другой рассматриваемой величины.

Более сложные формы учитывают угловые отношения между расстоянием и физической величиной, но приведенные выше уравнения отражают существенную особенность момента, а именно существование лежащего в основе момента. $r^{n}\rho (r)$ или эквивалентный термин. Это означает, что существует несколько моментов (по одному для каждого значения n ) и что момент обычно зависит от контрольной точки, от которой расстояние $r$ измеряется, хотя для определенных моментов (технически, наименьшего ненулевого момента) эта зависимость исчезает и момент становится независимым от точки отсчета.

Каждое значение n соответствует разному моменту: 1-й момент соответствует n = 1; 2-й момент при n = 2 и т. д. 0-й момент ( n = 0) иногда называют монопольным моментом ; 1-й момент ( n = 1) иногда называют дипольным моментом , а 2-й момент ( n = 2) иногда называют квадрупольным моментом , особенно в контексте распределения электрического заряда.

Примеры

• Момент силы , или крутящий момент , — это первый момент: $\mathbf {\tau } =rF$или, в более общем смысле, $\mathbf {r} \times \mathbf {F}$.
• Аналогично, угловой момент — это первый момент импульса : $\mathbf {L} =\mathbf {r} \times \mathbf {p}$. Импульс сам по себе не является моментом.
• Электрический дипольный момент также является первым моментом: $\mathbf {p} =q\,\mathbf {d}$ для двух противоположных точечных зарядов или ${\textstyle \int \mathbf {r} \,\rho (\mathbf {r} )\,d^{3}r}$ для распределенного заряда с плотностью заряда $\rho (\mathbf {r} )$.

Моменты массы:

• Полная . масса – это нулевой момент массы
• Центром масс является 1-й момент массы, нормированный на полную массу: ${\textstyle \mathbf {R} ={\frac {1}{M}}\sum _{i}\mathbf {r} _{i}m_{i}}$ для сбора точечных масс или ${\textstyle {\frac {1}{M}}\int \mathbf {r} \rho (\mathbf {r} )\,d^{3}r}$ для объекта с массовым распределением $\rho (\mathbf {r} )$.
• Момент инерции – это 2-й момент массы: $I=r^{2}m$ для точечной массы, ${\textstyle \sum _{i}r_{i}^{2}m_{i}}$ для сбора точечных масс или ${\textstyle \int r^{2}\rho (\mathbf {r} )\,d^{3}r}$ для объекта с массовым распределением $\rho (\mathbf {r} )$. За точку отсчета часто (но не всегда) принимают центр масс.

Многополюсные моменты

Предполагая, что функция плотности конечна и локализована в определенной области, за пределами этой области 1/ r потенциал может быть выражен как серия сферических гармоник :

$\Phi (\mathbf {r} )=\int {\frac {\rho (\mathbf {r'} )}{|\mathbf {r} -\mathbf {r'} |}}\,d^{3}r'=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {4\pi }{2\ell +1}}\right)q_{\ell m}\,{\frac {Y_{\ell m}(\theta ,\varphi )}{r^{\ell +1}}}$

Коэффициенты $q_{\ell m}$ известны как мультипольные моменты и принимают вид:

$q_{\ell m}=\int (r')^{\ell }\,\rho (\mathbf {r'} )\,Y_{\ell m}^{*}(\theta ',\varphi ')\,d^{3}r'$

где $\mathbf {r} '$ выраженный в сферических координатах $\left(r',\varphi ',\theta '\right)$ является переменной интегрирования. Более полное описание можно найти на страницах, описывающих мультипольное расширение или сферические мультипольные моменты . (Условия в приведенных выше уравнениях были взяты из Джексона – соглашения, используемые на указанных страницах, могут немного отличаться.)

Когда $\rho$ представляет собой плотность электрического заряда, $q_{lm}$ в некотором смысле являются проекциями моментов электрического заряда: $q_{00}$ – монопольный момент; тот $q_{1m}$ являются проекциями дипольного момента, $q_{2m}$ являются проекциями квадрупольного момента и т. д.

Применение

Мультипольное разложение применимо к 1/ r скалярным потенциалам, примеры которых включают электрический потенциал и гравитационный потенциал . Для этих потенциалов выражение можно использовать для аппроксимации напряженности поля, создаваемого локализованным распределением зарядов (или массы), путем расчета первых нескольких моментов. При достаточно большом r разумное приближение можно получить, исходя только из монопольного и дипольного моментов. Более высокая точность может быть достигнута за счет расчета моментов более высокого порядка. Расширения метода можно использовать для расчета энергий взаимодействия и межмолекулярных сил.

Этот метод также можно использовать для определения свойств неизвестного распределения. $\rho$. Измерения, относящиеся к мультипольным моментам, могут быть проведены и использованы для определения свойств основного распределения. Этот метод применим к небольшим объектам, таким как молекулы, но также применимо и к самой Вселенной, например, метод, используемый в экспериментах WMAP и Planck для анализа космического микроволнового фонового излучения.

История

Рычаг в равновесии

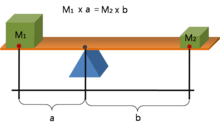
В произведениях, которые, как полагают, происходят из Древней Греции , понятие момента упоминается словом ῥοπή ( rhopḗ , букв. «наклон») и такими составными словами, как ἰσόρροπα ( isorropa , букв. «равных наклонностей»). Контекст этих работ – механика и геометрия с участием рычага . В частности, в дошедших до нас работах, приписываемых Архимеду , момент указывается в таких формулировках:

« Соизмеримые величины ( σύμμετρα μεγέθεα ) [А и В] одинаково уравновешены ( ἰσορροπέοντι ) если их расстояния [до центра Г, т. е. АГ и ВВ] обратно пропорциональны ( ἀντιπεπονθοτως ) их весам ( varēsin )».

Более того, в дошедших до нас текстах, таких как «Метод механических теорем» , моменты используются для определения центра тяжести , площади и объема геометрических фигур.

В 1269 году Вильгельм Мербеке различные произведения Архимеда и Евтоция переводит на латынь . Термин ῥοπή транслитерируется как ropen .

Около 1450 года Якоб Кремонский переводит ῥοπή в подобных текстах на латинский термин «импульс » ( букв. «движение»). ). Тот же термин сохранен в переводе 1501 года Джорджио Валлы , а впоследствии Франческо Мауролико , Федерико Коммандино , Гвидобальдо дель Монте , Адриана ван Роомена , Флоренс Риво , Франческо Буонамичи , Марина Мерсенна. и Галилео Галилей . Однако почему слово «импульс» для перевода было выбрано ? Одна из подсказок, по мнению Треккани , заключается в том, что momento в средневековой Италии, где жили первые переводчики, в переносном смысле означал одновременно и «момент времени», и «момент веса» (небольшое количество веса, которое меняет чашу весов). ).

В 1554 году Франческо Мауролико уточняет латинский термин «импульс» в работе «Прологи sive проповеди» . Вот перевод с латыни на английский, сделанный Маршаллом Кладжеттом :

«[...] равные гири на неравных расстояниях не имеют одинакового веса, но неравные гири [на этих неравных расстояниях могут] весить одинаково. Ибо гиря, подвешенная на большем расстоянии, тяжелее, что очевидно на весах . Следовательно, существует существует некий третий вид силы или третья разница величины, которая отличается как от тела, так и от веса, и которую они называют моментом . Следовательно, тело приобретает вес как за счет количества (т. е. размера), так и за счет качества (т. е. материала), но вес получает свой момент от расстояния, на котором оно подвешено. Следовательно, когда расстояния обратно пропорциональны весам, моменты [весов] равны, как Архимед показал в «Книге о равных моментах» . Следовательно, веса или [скорее] моменты, как и другие непрерывные величины, соединяются в каком-то общем конце, то есть в чем-то общем для них обоих, например, в центре тяжести или в точке равновесия. Центром тяжести любого груза является та точка, которая, независимо от того, как часто и когда бы тело ни подвешивалось, всегда наклоняется перпендикулярно к универсальному центру.

Помимо тела, веса и момента, существует некая четвертая сила, которую можно назвать импульсом или силой. Аристотель исследует ее в «Вопросах механики» , и она совершенно отлична от [трех] вышеупомянутых [степеней или величин]. [...]"

В 1586 году Саймон Стевин использует голландский термин staltwicht («припаркованный вес») для обозначения импульса в De Beghinselen Der Weeghconst .

В 1632 году Галилео Галилей публикует «Диалог о двух главных мировых системах» и использует итальянский momento во многих значениях, в том числе у своего предшественника.

некоторые произведения Галилея В 1643 году Томас Солсбери переводит на английский язык . Салусбери переводит латинский импульс и итальянский момент на английский термин момент .

В 1765 году латинский термин «момент инерции» ( английский : момент инерции использовал Леонард Эйлер ) для обозначения одной из величин Христиана Гюйгенса в «Horologium Oscillatorium» . Работа Гюйгенса 1673 года по поиску центра колебаний была стимулирована Марином Мерсенном , который предложил ему это в 1646 году.

В 1811 году французский термин «момент силы» ( английский : момент силы ) по отношению к точке и плоскости используется Симеоном Дени Пуассоном в «Трактате о механике» . Английский перевод появляется в 1842 году.

В 1884 году термин крутящий момент предложил Джеймс Томсон в контексте измерения сил вращения машин (с гребными винтами и роторами ). Сегодня динамометр используется для измерения крутящего момента машин.

В 1893 году Карл Пирсон использовал термин n-й момент и $\mu _{n}$ в контексте соответствующих кривой . научных измерений, Пирсон написал в ответ Джону Венну , который несколькими годами ранее заметил своеобразную закономерность, связанную с метеорологическими данными, и попросил объяснить ее причину. В ответе Пирсона используется эта аналогия: механический «центр тяжести» — это среднее значение , а «расстояние» — это отклонение от среднего значения. Позже это переросло в моменты в математике . Аналогия между механическим понятием момента и статистической функцией, включающей сумму отклонений в n-й степени, была замечена несколькими ранее, в том числе Лапласом , Крампом , Гауссом , Энке , Чубером , Кетле и Де Форестом .

См. также

• Крутящий момент (или момент силы ), см. также статью пара (механика)
• Момент (математика)
• Механическое равновесие применяется, когда объект сбалансирован так, что сумма моментов по часовой стрелке относительно оси вращения равна сумме моментов против часовой стрелки относительно того же центра вращения.
• Момент инерции $\left(I=\Sigma mr^{2}\right)$, аналог массы в обсуждении вращательного движения. Это мера сопротивления объекта изменениям скорости его вращения.
• Момент импульса $(\mathbf {L} =\mathbf {r} \times m\mathbf {v} )$, вращательный аналог линейного импульса .
• Магнитный момент $\left(\mathbf {\mu } =I\mathbf {A} \right)$, дипольный момент, измеряющий силу и направление магнитного источника.
• Электрический дипольный момент — дипольный момент, измеряющий разницу зарядов и направление между двумя или более зарядами. Например, электрический дипольный момент между зарядами – q и q, разделенными расстоянием d, равен $(\mathbf {p} =q\mathbf {d} )$
• Изгибающий момент — момент, приводящий к изгибу элемента конструкции.
• Первый момент площади — свойство объекта, связанное с его сопротивлением сдвиговому напряжению.
• Второй момент площади — свойство объекта, связанное с его сопротивлением изгибу и отклонению.
• Полярный момент инерции — свойство объекта, связанное с его сопротивлением кручению.
• Моменты изображения , статистические свойства изображения.
• Сейсмический момент , величина, используемая для измерения силы землетрясения.
• Плазменные моменты , жидкостное описание плазмы с точки зрения плотности, скорости и давления.
• Список моментов инерции площади
• Список моментов инерции
• Многополюсное расширение
• Сферические мультипольные моменты

Внешние ссылки

• СМИ, связанные с моментом (физикой) , на Викискладе?
• [1] Словарное определение момента.