О равновесии плоскостей
 | |
| Автор | Архимед |
|---|---|
| Язык | Древнегреческий |
| Жанр | Физика , Геометрия |
О равновесии плоскостей ( древнегреческий : Περὶ ἐπιπέδων ἱσορροπιῶν , латинизированный : perí epipédōn isorropiôn ) — трактат Архимеда в двух книгах. Первая книга содержит доказательство закона рычага завершается положениями о центре тяжести треугольника и трапеции и . [1] [2] Вторая книга, содержащая десять положений , исследует центры тяжести параболических отрезков. [1]
Согласно Паппу Александрийскому , работа Архимеда над рычагами и его понимание механического преимущества заставили его сказать: «Дайте мне точку опоры, и я переверну Землю» (древнегреческий: δός μοί ποῦ στῶ καὶ κινῶ τὴν γῆν латинизировано : dṓs moi poû stṓ kaí kinô tḗn gên ), хотя другие древние свидетельства неоднозначны относительно контекста поговорки. [3] [4]
Обзор
[ редактировать ]Рычаг и его свойства были хорошо известны еще до Архимеда, и он был не первым, кто дал анализ задействованного принципа. [5] Более ранние «Проблемы механики» , когда-то приписываемые Аристотелю, но, скорее всего, написанные одним из его преемников, содержат слабое доказательство закона рычага без использования концепции центра тяжести. Есть еще одна короткая работа, приписываемая Евклиду, под названием «О весах» , которая также содержит математическое доказательство закона, опять же без обращения к центру тяжести. [6]
Напротив, в работе Архимеда решающее значение имеет понятие центра тяжести. [7] В книге «О равновесии плоскостей I», которая содержит семь постулатов и пятнадцать предложений, центр тяжести используется как для соизмеримых, так и для несоизмеримых величин, чтобы оправдать закон рычага, хотя некоторые аргументы не являются удовлетворительными. [2] Затем Архимед приступает к определению центра тяжести параллелограмма и треугольника , заканчивая первую книгу доказательством центра тяжести трапеции .
Книга «О равновесии самолетов II» имеет ту же тему, что и первая книга, но, скорее всего, была написана позже. Он содержит десять положений относительно центра тяжести исключительно параболических сегментов и исследует эти сегменты, заменяя их прямоугольниками равной площади. Этот обмен стал возможным благодаря результатам, полученным в «Квадратуре параболы» , трактате, предположительно опубликованном после первой книги « О равновесии плоскостей» . [1] [2]
Содержание
[ редактировать ]Забронируйте один
[ редактировать ]Первая половина книги посвящена свойствам баланса и закону рычага, а вторая половина посвящена центру тяжести основных плоских фигур. Аргумент, устанавливающий закон рычага, использует, в частности, первый постулат, который гласит, что «равные веса на равных расстояниях находятся в равновесии». В предложениях 4 и 5 Архимед расширяет этот постулат, доказывая, что центр тяжести любой системы, состоящей из четного числа равных весов, равномерно распределенных, будет расположен в средней точке между двумя центрами весов. Затем Архимед использует эти теоремы для доказательства закона рычага в предложении 6 (для соизмеримых случаев) и предложении 7 (для несоизмеримых случаев).
Теорема

Учитывая две неравные, но соизмеримые массы и плечо рычага, разделенное на две неравные, но соизмеримые части (см. рисунок напротив), если величины A и B приложены к точкам E и D соответственно, система будет находиться в равновесии, если веса обратно пропорциональны длинам:
Доказательство
Предположим, что линии и веса построены по правилу с использованием общей меры (или единицы) N и в соотношении четыре к трем. Теперь увеличьте длину ЭД вдвое, скопировав более длинную руку слева и более короткую руку справа.
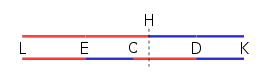
Для демонстрации измените порядок строк так, чтобы CD был рядом с LE (две красные линии вместе), и сопоставьте их с оригиналом (как показано ниже):
Ясно, что обе линии в два раза длиннее исходной линии ED, что LH имеет центр в E, а HK имеет центр в D. Кроме того, обратите внимание, что EH (которая равна CD) несет общую меру (или единица измерения) N точное количество раз, как и EC и, как следствие, CH. Остаётся доказать, что А, приложенный к Е, и Б, приложенный к D, будут иметь центр тяжести в С.
Следовательно, поскольку отношение LH к HK удвоило исходные расстояния CD и EC, аналогичным образом разделите величины A и B на соотношение восемь к шести (преобразование, которое сохраняет их исходное соотношение четыре к трем) и выровняйте их так. что блоки A (красные) сосредоточены на E, а блоки B (синие) — на D.
Теперь, поскольку четное количество одинаковых гирь, расположенных на одинаковом расстоянии, имеют центр тяжести между двумя средними гирями, фактически А применяется в точке Е, а В — в точке D, как того требует предложение. Далее, вся система состоит из четного числа равных грузов, равномерно распределенных, и, следовательно, по тому же закону С должен быть центром тяжести всей системы. Таким образом, система не наклоняется, а находится в равновесии. [1]
Книга вторая
[ редактировать ]Основная цель второй книги « О равновесии плоскостей» — определение центра тяжести любой части параболического сегмента, как показано в предложении 8.
Книга начинается с более простого доказательства закона рычага в предложении 1 со ссылкой на результаты, полученные в квадратуре параболы . Архимед доказывает следующие семь положений, комбинируя понятие центра тяжести и свойства параболы с результатами, полученными ранее в книге « О равновесии плоскостей I». В частности, он делает вывод, что две параболы, равные по площади, имеют свой центр тяжести. равноудалены от некоторой точки, а позже заменяет их площади прямоугольниками равной площади. [1]
Последние два предложения, предложения 9 и 10, довольно тупы, но сосредоточены на определении центра тяжести фигуры, отрезанной от любого параболического сегмента усеченной пирамидой . [8]
Наследие
[ редактировать ]Механические работы Архимеда, в том числе «О равновесии плоскостей» , были известны, но мало читались в древности. И Герой , и Папп ссылаются на Архимеда в своих работах по механике, в основном в дискуссиях о центре тяжести и механическом преимуществе . Некоторые римские авторы, такие как Витрувий , по-видимому, также имели некоторое представление о творчестве Архимеда. [9] [10]
В средние века некоторые арабские авторы были знакомы с работами Архимеда о балансах и центре тяжести и расширили их; однако на Латинском Западе эти идеи были практически неизвестны, за исключением нескольких ограниченных случаев. [11] [12] Лишь в эпоху позднего Возрождения результаты, полученные в «О равновесии плоскостей», начали широко распространяться. Математический подход Архимеда к физике , в частности, стал моделью для последующих учёных, таких как Гвидобальдо дель Монте , Бернардино Бальди , Симон Стевин и Галилео Галилей . [13] [14]
Понятие центра тяжести достигло высокого уровня сложности в первой половине XVII века , особенно в работах Евангелисты Торричелли и Христиана Гюйгенса , и сыграло решающую роль в развитии рациональной механики . [15] [16]
Критика
[ редактировать ]Ряд исследователей выявили несоответствия в первой книге « О равновесии плоскостей» . [2] [17] Берггрен подвергает сомнению подлинность почти половины первой книги, отмечая, например, избыточность предложений 1–3 и 11–12. Однако он следует за Дейкстерхейсом , отвергая критику Маха в отношении предложения 6, которое действительно доказывает, что «если система гирь, подвешенная на балансире, находится в равновесии, когда она поддерживается в определенной точке, то любое перераспределение этих гирь, сохраняющее их общий центр гравитации, также сохраняет равновесие». [2] [8]
Кроме того, предложение 7 первой книги в его нынешнем виде выглядит неполным, так что, строго говоря, Архимед в первой книге демонстрирует закон рычага только для соизмеримых величин. [1] [2] Вторая книга « О равновесии плоскостей» не затронута этими недостатками, поскольку, за исключением первого положения, рычаг вообще не рассматривается. [8] В дошедших до нас работах Архимеда также нет определения центра тяжести, что, по мнению некоторых ученых, затрудняет прослеживание (или обоснование) логической структуры некоторых из его аргументов в « О равновесии плоскостей» . [5] [7]
Ссылки
[ редактировать ]- ^ Jump up to: Перейти обратно: а б с д и ж Хит, ТЛ (1897 г.). «Труды Архимеда (1897). Полный труд в формате PDF (19 МБ)» . Издательство Кембриджского университета. Архивировано из оригинала 6 октября 2007 года . Проверено 6 января 2013 г.
- ^ Jump up to: Перейти обратно: а б с д и ж Берггрен, Дж. Л. (1976). «Ложные теоремы Архимеда о равновесии плоскостей, книга I». Архив истории точных наук . 16 (2): 87–103. дои : 10.1007/BF00349632 . ISSN 1432-0657 . S2CID 119741769 .
- ↑ Цитируется Паппом Александрийским в Синагоге , Книга VIII, стр. 1060 в изд. Хульч
- ^ Берриман, С. (2020). «Как Архимед предлагал переместить Землю» . Исида . 111 (3): 562–567. дои : 10.1086/710317 . ISSN 0021-1753 . S2CID 224841008 .
- ^ Jump up to: Перейти обратно: а б Гоу, Г. (1972). «Теория рычага Архимеда и критика Маха» . Исследования по истории и философии науки . Часть А. 2 (4): 329–345. Бибкод : 1972ШПСА...2..329Г . дои : 10.1016/0039-3681(72)90002-7 . ISSN 0039-3681 .
- ^ Ренн, Дж., Дамероу, П. и Маклафлин, П. (2003). Аристотель, Архимед, Евклид и происхождение механики: взгляд на историческую эпистемологию. В книге Дж. Л. Монтесинос Сирера (ред.), Симпозиум Архимеда, Канарский фонд истории науки Оротавы (стр. 43–59). http://www.mpig-berlin.mpg.de/Preprints/P239.PDF.
- ^ Jump up to: Перейти обратно: а б Магнаги, CP; Ассис, АКТ (07 мая 2012 г.). «Расчет центра тяжести конуса по методу Архимеда» . Европейский журнал физики . 33 (3): 637–646. Бибкод : 2012EJPh...33..637M . дои : 10.1088/0143-0807/33/3/637 . hdl : 20.500.12733/1666778 . ISSN 0143-0807 . S2CID 54012592 .
- ^ Jump up to: Перейти обратно: а б с Дейкстерхейс, Э.Дж. (1987). Архимед . Издательство Принстонского университета, Принстон. ISBN 0-691-08421-1 . Переизданный перевод исследования Архимеда и его работ 1938 года, сделанный историком науки.
- ^ Драхманн, АГ (1968). «Архимед и физика» . Центавр . 12 (1): 1–11. Бибкод : 1968Cent...12....1D . дои : 10.1111/j.1600-0498.1968.tb00074.x . ISSN 0008-8994 .
- ^ Ассис, АКТ (2010). Архимед, центр гравитации и первый закон механики (2-е изд.). Компания C. Roy Keys Incorporated. ISBN 9780986492648 .
- ^ Клагетт, М. (1959). «Влияние Архимеда на средневековую науку» . Исида . 50 (4): 419–429. дои : 10.1086/348797 . ISSN 0021-1753 . JSTOR 226426 . S2CID 145737269 .
- ^ Хойруп Дж. (2019), Хойруп Дж. (редактор), «(Статья I.16.) Архимед - знания и знания от латинской античности до уходящего европейского Возрождения» , Избранные очерки по математической практике до и раннего Нового времени , Чам: Springer International Publishing, стр. 459–477, doi : 10.1007/978-3-030-19258-7_17 , ISBN 978-3-030-19258-7 , S2CID 193706291
- ^ Палмиери, П. (2008). «Разрыв круга: возникновение архимедовой механики в эпоху позднего Возрождения» . Архив истории точных наук . 62 (3): 301–346. дои : 10.1007/s00407-007-0012-8 . ISSN 1432-0657 . S2CID 121698785 .
- ^ Мели, Д. (2010). «Аксиоматическая традиция в механике XVII века» . Рассуждение о новом методе: возрождение брака истории и философии науки . Открытый суд. стр. 23–41. ISBN 978-0-8126-9662-2 .
- ^ Пизано, Р.; Буссотти, П.; Буссотти, Паоло; Буссотти, Паоло (2014). «Заметки о механике и математике у Торричелли как соотношения физики и математики в истории науки» . Проблемы образования в 21 веке . 61 : 88–97. дои : 10.33225/pec/14.61.88 . ISSN 1822-7864 .
- ^ Ван Дейк, М. (2020), «Механическая философия: наука о механике» , Энциклопедия ранней современной философии и наук , Springer, стр. 1–11, hdl : 1854/LU-8678741 , ISBN 978-3-319-20791-9
- ^ Мах, Э. (1907). Наука механика: критический и исторический отчет о ее развитии . Открытый суд, Чикаго. Переизданный перевод оригинала 1883 года Томаса Дж. МакКормака . Эд. 3, ред.