Саймон Стевин

Чтобы узнать о корабле, см. RV Simon Stevin . О голландском академическом журнале см. Simon Stevin (журнал) .

Саймон Стевин
Рожденный	1548 Брюгге, Бельгия
Умер	1620 г. (71–72 года) Гаага?
Альма-матер	Лейденский университет
Занятия	Математик учёный теоретик музыки
Известный	Десятичные дроби Эксперимент с Делфтской башней Теорема о промежуточном значении Закон Стевина

Саймон Стевин (англ. Голландский: [ˈsimɔn steːˈvɪn] ; 1548–1620), иногда называемый Стевинусом , был фламандским математиком , учёным и теоретиком музыки . Он внес различные вклады во многие области науки и техники , как теоретические, так и практические. Он также перевел различные математические термины на голландский язык , сделав его одним из немногих европейских языков, в котором слово математика , вискунде ( wis и kunde , т.е. «знание того, что достоверно»), было не заимствованным из греческого языка , а заимствованным. калька через латынь . Он также заменил слово chemie , что по-голландски означает химия, на scheikunde («искусство разделения»), сделанное по аналогии с wiskunde .

Биография

О жизни Саймона Стевина достоверно известно очень мало, и то, что мы знаем, в основном выведено из других зафиксированных фактов. Точная дата рождения, а также дата и место его смерти неизвестны. Предполагается, что он родился в Брюгге , поскольку поступил в Лейденский университет под именем Саймон Стевинус Брюгенсис (что означает «Саймон Стевин из Брюгге»). Его имя обычно пишется как Стевин, но в некоторых документах, касающихся его отца, используется написание Стевин (произношение [ˈste:vεɪn]); это было обычное изменение правописания в голландском языке 16 века. Мать Саймона Стевина, Катилина (или Кейтлин), была дочерью богатой семьи из Ипра ; ее отец Хуберт был бедняком из Брюгге. Позже Кателин выйдет замуж за Йоста Сайона, который занимался торговлей коврами и шелком и был членом schuttersgilde Синт -Себастьян. Благодаря замужеству Кателийна стала членом семьи кальвинистов ; Считается, что Симон Стевин, вероятно, был воспитан в кальвинистской вере.

Считается, что Стевин вырос в относительно богатой среде и получил хорошее образование. Вероятно, он получил образование в латинской школе в своем родном городе.

Путешествия Саймона Стевина

Стевин покинул Брюгге в 1571 году, очевидно, не имея конкретного пункта назначения. Стевин, скорее всего, был кальвинистом, поскольку католик, скорее всего, не поднялся бы до доверенного положения, которое он позже занял у Мориса, принца Оранского . Предполагается, что он покинул Брюгге, спасаясь от религиозных преследований протестантов со стороны испанских правителей. На основании ссылок в его работе «Wisconstighe Ghedaechtenissen» («Математические мемуары») был сделан вывод, что он, должно быть, сначала переехал в Антверпен, где начал свою карьеру в качестве торгового клерка . Некоторые биографы упоминают, что между 1571 и 1577 годами он путешествовал по Пруссии , Польше , Дании , Норвегии , Швеции и другим частям Северной Европы . Вполне возможно, что эти путешествия он совершал в течение более длительного периода времени. В 1577 году Симон Стевин вернулся в Брюгге и был назначен городским клерком Брюгге олдерменами , эту должность он занимал с 1577 по 1581 год. Он работал в офисе Яна де Брюне в Брюгге Врие , замке Брюгге.

Почему он вернулся в Брюгге в 1577 году, неясно. Возможно, это было связано с политическими событиями того периода. Брюгге был ареной ожесточенного религиозного конфликта. Католики и кальвинисты попеременно контролировали правительство города. Обычно они противостояли друг другу, но иногда сотрудничали, чтобы противодействовать диктату короля Испании Филиппа II . В 1576 году был установлен определенный уровень официальной религиозной терпимости. Это могло объяснить, почему Стевин вернулся в Брюгге в 1577 году. Позже кальвинисты захватили власть во многих фламандских городах и заключили в тюрьмы католических священнослужителей и светских губернаторов, поддерживающих испанских правителей. Между 1578 и 1584 годами Брюгге находился под властью кальвинистов.

Нидерландах

В 1581 году Стевин снова покинул родной Брюгге и переехал в Лейден , где посещал латинскую школу. 16 февраля 1583 года он поступил под именем Саймон Стевинус Бругенсис (что означает «Саймон Стевин из Брюгге») в Лейденский университет , основанный Вильгельмом Безмолвным в 1575 году. Здесь он подружился со вторым сыном и наследником Вильгельма Безмолвного, принцем Морисом. , граф Нассау. Стевин числится в реестрах университета до 1590 года и, по-видимому, так и не окончил его.

После убийства Вильгельма Молчаливого и вступления принца Мориса на пост отца Стевин стал главным советником и наставником принца Мориса. Принц Морис много раз спрашивал его совета и назначил его государственным служащим – сначала директором так называемого «водного государства». (государственный орган по общественным работам , особенно водному хозяйству) с 1592 года, а затем генерал-квартирмейстер армии Генеральных штатов. Принц Морис также попросил Стевина основать инженерную школу при Лейденском университете.

Стевин переехал в Гаагу , где купил дом в 1612 году. Он женился в 1610 или 1614 году и имел четверых детей. Известно, что он остался вдовой с двумя детьми. после смерти в Лейдене или Гааге в 1620 году

• 
  Статуя Симона Стевина работы Эжена Симониса на площади Саймона Стевинплейн в Брюгге
• 
  Статуя Стевина (фрагмент)
• 
  Статуя (фрагмент): Схема наклонной плоскости.
• 
  Статуя (фрагмент), показывающая эксперименты по гидростатическому равновесию.

Открытия и изобретения

Ветряная колесница или сухопутная яхта (Zeilwagen), спроектированная Саймоном Стевином для принца Мориса Оранского (гравюра Жака де Гейна).

Стевину принадлежит множество открытий и изобретений. Стевин написал множество бестселлеров и был пионером в развитии и практическом применении (связанных с инженерией) наук, таких как математика , физика и прикладных наук, таких как гидротехника и геодезия . Считалось, что он изобрел десятичные дроби до середины 20-го века, когда исследователи обнаружили, что десятичные дроби были ранее введены средневековым исламским ученым аль-Уклидиси в книге, написанной в 952 году. было дано задолго до Стевина в книге «Мифтах аль-Хисаб», написанной в 1427 году Аль-Каши .

Современников больше всего поразило изобретение им так называемой сухопутной яхты — кареты с парусами, модель которой сохранилась в Схевенингене до 1802 года. Сама карета была утеряна задолго до этого. Примерно в 1600 году Стевин с принцем Морисом Оранским и еще двадцатью шестью людьми воспользовался каретой на пляже между Схевенингеном и Петтеном . Карета приводилась в движение исключительно силой ветра и приобретала скорость, превосходящую скорость лошадей.

Управление водными путями

Работа Стевина в водном штате включала усовершенствование шлюзов и водосбросов для борьбы с наводнениями , упражнения по гидротехнике . Ветряные мельницы уже использовались для откачки воды, но в Ван де Моленсе ( «О мельницах ») он предложил улучшения, включая идеи о том, что колеса должны двигаться медленно с лучшей системой зацепления зубьев шестерни . Это в три раза повысило эффективность ветряных мельниц, используемых для откачки воды из польдеров . он получил в 1586 году. Патент на свое изобретение

Философия науки

Целью Стевина было создать вторую эпоху мудрости , в которой человечество восстановило бы все свои прежние знания. Он пришел к выводу, что языком, на котором говорят в эту эпоху, должен быть голландский, потому что, как он показал эмпирически словами можно было обозначить больше понятий, , в этом языке односложными чем в любом из (европейских) языков, с которыми он его сравнивал. Это была одна из причин, почему он писал все свои произведения на голландском языке, оставляя их перевод другим. Другая причина заключалась в том, что он хотел, чтобы его работы были практически полезны людям, не владевшим общепринятым научным языком того времени — латынью. Благодаря Саймону Стевину голландский язык получил свой собственный научный словарь, такой как « wiskunde » ( «kunst van het gewisse of zekere», искусство того, что известно или что достоверно) для математики , « natuurkunde » («искусство природы»). ) для физики , « шейкунде » («искусство разделения») для химии , « стерренкунде » («искусство звезд») для астрономии , « меткунде » («искусство измерения») для геометрии .

Геометрия, физика и тригонометрия

Доказательство Стевина закона равновесия на наклонной плоскости , известное как «Эпитафия Стевина».

Стевин был первым, кто показал, как моделировать правильные и полуправильные многогранники , очерчивая их рамки на плоскости. Он также различал стабильное и нестабильное равновесие.

Стевин внес свой вклад в тригонометрию своей книгой De Driehuuckhandel .

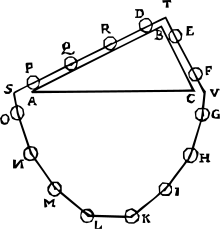
В первой книге «Начала искусства взвешивания», вторая часть: «О предложениях [Свойства наклонных гирь], стр. 41, теорема XI, предложение XIX» , Условие равновесия сил на наклонных плоскостях он вывел , используя схему с «венком», содержащим равномерно расположенные круглые массы, покоящиеся на плоскостях треугольной призмы (см. рисунок сбоку). Он пришел к выводу, что требуемые гири пропорциональны длинам сторон, на которые они опираются, при условии, что третья сторона горизонтальна, и что влияние гири уменьшается аналогичным образом. Подразумевается, что коэффициент приведения — это высота треугольника, деленная на сторону (синус угла стороны относительно горизонтали). Схема доказательства этой концепции известна как «Эпитафия Стевинуса». Как заметил Э. Дж. Дейкстерхейс , доказательство Стевина равновесия на наклонной плоскости можно ошибочно обвинить в том, что использование вечного движения подразумевает доведение до абсурда . Дейкстерхейс говорит, что Стевин «интуитивно использовал принцип сохранения энергии … задолго до того, как он был сформулирован явно».

разрешение сил , хотя оно и является простым следствием закона их состава. Он продемонстрировал перед Пьером Вариньоном не отмеченное ранее

Стевин открыл гидростатический парадокс , который гласит, что давление в жидкости не зависит от формы сосуда и площади основания, а зависит исключительно от его высоты.

Он также дал меру давления на любой части стенки сосуда.

Он был первым, кто объяснил приливы и отливы, используя притяжение Луны .

В 1586 году он продемонстрировал , что два предмета разного веса падают с одинаковым ускорением.

Теория музыки

Ван де Шпигелинг дер Singconst .

Первое упоминание о равном темпераменте, связанном с корнем двенадцатой степени из двух, на Западе появилось в незаконченной рукописи Саймона Стевина « Ван де Шпигелинг дер сингконст » (около 1605 г.), опубликованной посмертно, триста лет спустя, в 1884 году; однако из-за недостаточной точности его расчетов многие полученные им числа (длины строки) отличались на одну или две единицы от правильных значений. Похоже, его вдохновили сочинения итальянского лютниста и теоретика музыки Винченцо Галилея (отца Галилео Галилея ), бывшего ученика Джозеффо Зарлино .

Бухгалтерия

Двойная бухгалтерия, возможно, была известна Стевину, поскольку в молодые годы он работал клерком в Антверпене , либо практически, либо благодаря работам итальянских авторов, таких как Лука Пачоли и Джероламо Кардано . Однако Стевин был первым, кто рекомендовал использовать обезличенные счета в домашнем хозяйстве. Он применил это на практике для принца Мориса и рекомендовал французскому государственному деятелю Сюлли .

Десятичные дроби

Стевин написал 35-страничный буклет под названием De Thiende («Искусство десятых»), впервые опубликованный на голландском языке в 1585 году и переведенный на французский язык как La Disme . Полное название английского перевода было «Десячная арифметика» : обучение тому, как выполнять все вычисления с целыми числами без дробей , используя четыре принципа общей арифметики: а именно: сложение , вычитание , умножение и деление . Понятия, упомянутые в буклете, включали дроби единиц и египетские дроби . Мусульманские математики были первыми, кто начал широко использовать десятичные дроби вместо дробей. Аль-Каши Книга «Ключ к арифметике » была написана в начале 15 века и послужила стимулом для систематического применения десятичных дробей к целым числам и их дробям. Но до Стевина никто не установил их ежедневное употребление. Он чувствовал, что это нововведение было настолько значительным, что объявил повсеместное введение десятичной чеканки, мер и весов всего лишь вопросом времени.

Его обозначения довольно громоздки. Точка , отделяющая целые числа от десятичных дробей, по-видимому, является изобретением Варфоломея Питиска , в тригонометрических таблицах которого (1612 г.) она встречается, и была принята Джоном Нейпиром в его логарифмических работах (1614 и 1619 гг.).

Стевин нарисовал маленькие кружочки вокруг показателей различных степеней одной десятой. То, что Стевин намеревался использовать эти цифры в кружочках для обозначения простых показателей степени, ясно из того факта, что он использовал тот же символ для степеней алгебраических величин. Он не избегал дробных показателей; в его работах не фигурируют только отрицательные показатели.

Стевин писал и на другие научные темы – например, по оптике, географии, астрономии – и ряд его сочинений был переведен на латынь В. Снеллиусом ( Виллеброрд Снелл ). Есть два полных издания его произведений на французском языке, оба напечатаны в Лейдене: одно в 1608 году, другое в 1634 году.

Математика

Математические труды , 1634 г.

Стевин написал свою «Арифметику» в 1594 году. Эта работа впервые принесла западному миру общее решение квадратного уравнения , первоначально задокументированное почти тысячелетием ранее Брахмагуптой в Индии.

По словам Ван дер Вардена , Стевин устранил «классическое ограничение «числ» целыми числами (Евклид) или рациональными дробями (Диофант)... действительные числа образовывали континуум. Его общее представление о действительном числе было принято, молчаливо или явно всеми более поздними учёными». Недавнее исследование приписывает Стевину большую роль в определении реальных цифр, чем это признают последователи Вейерштрасса . Стевин доказал теорему о промежуточном значении для многочленов, предвосхитив Коши ее доказательство . Стевин использует процедуру «разделяй и властвуй» , разделяя интервал на десять равных частей. Десятичные дроби Стевина послужили источником вдохновения для Исаака Ньютона работы о бесконечных рядах .

Неологизмы

Стевин считал, что голландский язык отлично подходит для написания научных статей, и перевел на него многие математические термины. В результате голландский является одним из немногих западноевропейских языков, в которых есть множество математических терминов, не происходящих из греческого или латыни. Сюда входит и само название «вискунде» (математика).

Его взгляд на важность того, чтобы научный язык был таким же, как язык ремесленника, можно показать из посвящения его книги De Thiende («Десме» или «Десятый»): «Саймон Стевин желает звездочетам, геодезистам, мерщикам ковров, мерщикам тела в целом, мерщикам монет и торговцам удачи». Далее в той же брошюре он пишет: «[этот текст] учит нас всем необходимым людям расчетам без использования дробей. Все действия можно свести к сложению, вычитанию, умножению и делению целых чисел».

Некоторые из изобретенных им слов эволюционировали: «aftrekken» ( «вычитать ») и «delen» ( «разделять ») остались прежними, но со временем «menigvuldigen» стало «vermenigvuldigen» ( «умножить », добавленное «ver» подчеркивает тот факт, что это действие). ). «Вергадерен» ( собрание ) превратилось в «оптеллен» ( добавить букв. « подсчитать» ).

Другой пример — голландское слово, обозначающее диаметр: «мидделлин», букв.: линия, проходящая через середину.

Слово «zomenigmaal» ( частное букв. «столько раз») было заменено на «частное» в современном голландском языке.

Другие термины не вошли в современный математический голландский язык, например, «тирлинг» ( умирать , хотя все еще используется в значении «умирать») вместо куба.

Общая информация

• Исследовательская ассоциация машиностроения Технологического университета Эйндховена , WSV Саймона Стевина, назван в честь Саймона Стевина. В память о Стевине ассоциация называет свой бар «De Weeghconst» и владеет собственным флотом сухопутных яхт .
• Стевин, которого называют Стевинусом, является одним из любимых авторов – если не любимым автором – дяди Тоби Шенди в Лоуренса Стерна книге «Жизнь и мнения Тристрама Шенди, джентльмен» .
• Цитата: Человек в гневе не умеет лукавить.
• В Брюгге есть площадь Симона Стевина, на которой установлена ​​статуя Стевина работы Эжена Симониса . Статуя включает в себя диаграмму наклонной плоскости Стевина.
• Из порта Остенде работает исследовательское судно RV Simon Stevin, названное в его честь.

Публикации

Укрепления Мёрса , спроектированные Саймоном Стевином.

Среди прочего он опубликовал:

• Тафелен ван Интерес (Таблицы процентов) в 1582 году с текущей стоимости задачами простых и сложных процентов, а также таблицами процентов, которые ранее не публиковались банкирами;
• Геометрические задачи 1583 г.;
• Де Тьенде ( La Disme , Десятый) в 1585 году, когда в Европе были введены десятичные дроби;
• Практика арифметики в 1585 году;
• «Арифметика» в 1585 году, в которой он представил единый подход к решению алгебраических уравнений ;
• Dialectike ofte bewysconst (Диалектика, или Искусство демонстрации) в 1585 году в Лейдене Кристоффеля Плантейна. Снова опубликовано в 1621 году в Роттердаме Яном ван Вэсберге де Йонге.
• De Beghinselen Der Weeghconst в 1586 году в сопровождении Де Вегдата ;
• De Beghinselen des Waterwichts (Принципы веса воды) в 1586 году на тему гидростатики ;
• Вита Политика . Назван Бургерлик Левен (Гражданская жизнь) в 1590 году;
• De Stercktenbouwing (Строительство укреплений ), опубликованная в 1594 году;
• «Де Хавенвиндинг» ( «Определение местоположения ») опубликовано в 1599 году;
• Де Хемеллопа в 1608 году, в котором он выразил поддержку теории Коперника .
• In Wiskonstighe Ghedachtenissen (Математические мемуары, латынь : Hypomnemata Mathematica ) с 1605 по 1608 год. Сюда вошли более ранние работы Саймона Стевина, такие как De Driehouckhandel ( Тригонометрия ), De Meetdaet ( Практика измерения ) и De Deursichtighe ( Перспектива ), которые он отредактировал и опубликовал. .;
• Castrametatio, то есть армейские измерения, и Nieuwe Maniere van Stercktebou Spilsluysen («Новые способы строительства шлюзов »), опубликованные в 1617 году;
• De Spiegheling der Singconst (Теория певческого искусства).
• «Математические труды...», Лейден, 1634 г.

Дальнейшее чтение

• Практически все сочинения Стевина были опубликованы в пяти томах с введением и анализом в: Кроун, Эрнст; Дейкстерхейс, Э.Дж. ; Форбс, Р.Дж.; и др., ред. (1955–1966). Основные произведения Саймона Стевина . Лиссе: Swets & Zeitlinger. Основные работы доступны в Интернете в Цифровой библиотеке Королевской Нидерландской академии искусств и наук . Не включает диалектику часто Bewysconst .
• Еще один хороший источник о Стевине — франкоязычный пакет: Королевская библиотека Бельгии, изд. (2004). Саймон Стевин (1548–1620): Возникновение новой науки . Тюрнхаут: Бреполи. .
• Недавняя работа о Саймоне Стевине на голландском языке: Девриз Дж. Т. и Ванден Берге Г. (2003). Чудо и неудивительно. Гениальный мир Симона Стевина 1548–1620 . Левен: Давидсфондс. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) .
• Недавняя работа о Саймоне Стевине на английском языке: Девриз, Дж. Т. и Ванден Берге, Г. (2007). Магия – это не магия. Чудесный мир Симона Стевина 1548–1620 . Саутгемптон: WITpress. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• ван ден Хеувел, К. (2005). Де Юисбу. Реконструкция незаконченного трактата по архитектуре и гражданскому строительству Саймона Стевина . Амстердам: KNAW Эдита. 545 стр. – Работа доступна онлайн – см. внешние ссылки.
• ван Бунге, Вип (2001). От Стевина до Спинозы: Очерк философии в Голландской республике семнадцатого века . Лейден: Брилл.

• Герберманн, Чарльз, изд. (1913). «Саймон Стевин» . Католическая энциклопедия . Нью-Йорк: Компания Роберта Эпплтона.
• Девиз Саймона Стевина «Чудо, а не чудо» : английская страница о Саймоне Стевине, поддерживаемая Эд Дэвидс Кэти Шриер, со ссылками на некоторые из его работ.
• 3 Quarks Daily — это короткое эссе о Саймоне Стевине, написанное С. Аббасом Разой в 3 Quarks Daily.
• Simonstevin.be — это интернет-библиография, посвященная Саймону Стевину.
• Локусы: Конвергенция рассматривает использование Стевином правила ложной позиции.
• Математические страницы
• Ссылка KNAW.nl на неопубликованный трактат Саймона Стевина по архитектуре, градостроительству и гражданскому строительству – К. ван ден Хеувел. Де Юисбу.