Наклонная плоскость

Наклонная плоскость , также известная как пандус , представляет собой плоскую опорную поверхность, наклоненную под углом к вертикальному направлению , причем один конец выше другого, используемый в качестве вспомогательного средства для подъема или опускания груза. ^[1]^[2]^[3]Наклонная плоскость — одна из шести классических простых машин, определенных учеными эпохи Возрождения. Наклонные плоскости используются для перемещения тяжелых грузов через вертикальные препятствия. Примеры варьируются от пандуса, используемого для погрузки товаров в грузовик, до человека, поднимающегося по пешеходному пандусу, до автомобиля или железнодорожного поезда, поднимающегося на уклон. ^[3]

Перемещение объекта вверх по наклонной плоскости требует меньше усилий , чем подъем его прямо вверх, но за счет увеличения пройденного расстояния. ^[4]Механическое преимущество наклонной плоскости, коэффициент уменьшения силы, равно отношению длины наклонной поверхности к высоте, которую она охватывает. Благодаря сохранению энергии одно и то же количество механической энергии ( работы требуется для подъема данного предмета на данное вертикальное расстояние ) , не считая потерь от трения , но наклонная плоскость позволяет совершить ту же работу с меньшей силой, приложенной над поверхностью. большее расстояние. ^[5]^[6]

Угол трения , ^[7] также иногда называют углом естественного откоса , ^[8]— максимальный угол, при котором груз может неподвижно лежать на наклонной плоскости за счет трения , не соскальзывая вниз. угол равен арктангенсу коэффициента статического трения между _Этот поверхностями. ^[8]

Две другие простые машины часто считаются производными от наклонной плоскости. ^[9] Клин можно рассматривать как движущуюся наклонную плоскость или две наклонные плоскости , соединенные в основании. ^[5] Винт вокруг представляет собой узкую наклонную плоскость, обернутую цилиндра . ^[5]

Этот термин также может относиться к конкретной реализации; прямой пандус, врезанный в крутой склон холма, для перевозки грузов вверх и вниз по холму. Сюда могут относиться автомобили, идущие по рельсам или подтянутые канатной системой; фуникулер Джонстаунская наклонная или канатная дорога , например плоскость .

Использует [ править ]

Наклонные плоскости широко используются в виде погрузочных рамп для погрузки и разгрузки грузов на грузовые автомобили, корабли и самолеты. ^[3] Пандусы для инвалидных колясок используются для того, чтобы люди в инвалидных колясках могли преодолевать вертикальные препятствия, не превышая при этом своих сил. Эскалаторы и наклонные конвейерные ленты также представляют собой формы наклонной плоскости. ^[6]На фуникулере или канатной дороге вагон поднимают по крутой наклонной плоскости с помощью тросов. Наклонные самолеты также позволяют безопасно опускать тяжелые хрупкие объекты, включая людей, на вертикальное расстояние, используя нормальную силу самолета для уменьшения силы гравитации . для самолетов Эвакуационные трапы позволяют людям быстро и безопасно спуститься на землю с высоты пассажирского авиалайнера .

Использование пандусов для погрузки автомобиля на грузовик

Погрузка грузовика на корабль с помощью рампы

аварийной эвакуации самолета Слайд

Пандус для инвалидных колясок в японском автобусе

Погрузочная рампа на грузовике

Другие наклонные плоскости встроены в постоянные конструкции. Дороги для транспортных средств и железные дороги имеют наклонные плоскости в виде пологих уклонов, пандусов и дамб , что позволяет транспортным средствам преодолевать вертикальные препятствия, такие как холмы, без потери сцепления с поверхностью дороги. ^[3] Аналогичным образом, пешеходные дорожки и тротуары имеют пологие пандусы, ограничивающие их наклон и гарантирующие пешеходам сохранение сцепления с дорогой. ^[1]^[4] Наклонные плоскости также используются в качестве развлечения, позволяющего людям контролируемо скатиться вниз, на игровых площадках , водных горках , лыжных склонах и в скейт-парках .

Земляной пандус (справа) , построенный римлянами в 72 году нашей эры для вторжения в Масаду , Израиль.

Пешеходный пандус, Паласио-ду-Планалто, Бразилиа

Джонстаунская наклонная плоскость, фуникулер .

Бирма-роуд, Ассам, Индия, через Бирму в Китай, гр. 1945 год

Наклонные самолеты в скейт-парке

История [ править ]

Доказательство Стевина

В 1586 году фламандский инженер Саймон Стевин (Стевинус) обнаружил механическое преимущество наклонной плоскости, аргументируя это использованием нитки бус. ^[10]Он представил себе две наклонные плоскости одинаковой высоты, но с разными углами наклона, расположенные спина к спине, как в призме ( А, В, С выше). На наклонные плоскости накинута петля из нити с бисеринками через равные промежутки, часть нити свисает вниз. действуют как грузы на плоскостях, удерживаемые силой натяжения струны в точке Т. Бусины, опирающиеся на плоскости , Аргументация Стевина звучит так: ^[10]^[11]^[12]

Струна должна быть неподвижной, в статическом равновесии . Если бы нить была тяжелее с одной стороны, чем другая, и начала бы скользить вправо или влево под собственным весом, то, когда каждая бусина переместилась бы в положение предыдущей бусины, нить была бы неотличима от своего первоначального положения и, следовательно, продолжала бы двигаться. быть неуравновешенным и скользить. Этот аргумент можно повторять бесконечно, в результате чего возникнет круговое вечное движение , что абсурдно. Следовательно, он неподвижен, силы с обеих сторон в точке Т ( выше ) равны.
Часть цепочки, свисающая ниже наклонных плоскостей, симметрична, с равным количеством бусинок с каждой стороны. Он оказывает одинаковую силу на каждую сторону струны. Поэтому эту часть струны можно отрезать по краям плоскостей (точки S и V) , оставив только бусинки, опирающиеся на наклонные плоскости, а эта оставшаяся часть все равно будет находиться в статическом равновесии.
Поскольку бусины располагаются на нити через равные промежутки, общее количество бусинок, поддерживаемых каждой плоскостью, общая нагрузка пропорциональна длине плоскости. Поскольку входная поддерживающая сила, натяжение струны, одинакова для обеих, механическое преимущество каждой плоскости пропорционально ее наклонной длине.

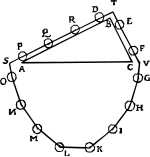
Как отметил Дейкстерхейс, ^[13]Аргументация Стевина не совсем убедительна. Силы, действующие на висячую часть цепи, не обязательно должны быть симметричными, поскольку висячая часть не обязана сохранять свою форму, когда ее отпускают. Даже если цепь отпускается с нулевым угловым моментом, движение, включая колебания, возможно, если цепь изначально не находится в равновесной конфигурации - предположение, которое сделало бы аргумент круговым.

Наклонные плоскости использовались людьми с доисторических времен для перемещения тяжелых предметов. ^[14]^[15]Наклонные дороги и дамбы , построенные древними цивилизациями, такими как римляне, являются примерами сохранившихся ранних наклонных плоскостей и показывают, что они понимали ценность этого устройства для перемещения предметов в гору. Тяжелые камни, используемые в древних каменных сооружениях, таких как Стоунхендж. ^[16] предположительно, были перемещены и установлены на месте с помощью наклонных плоскостей, сделанных из земли, ^[17]хотя трудно найти свидетельства существования таких временных пандусов. Египетские пирамиды были построены с использованием наклонных плоскостей. ^[18]^[19]^[20] Осадные пандусы позволяли древним армиям преодолевать крепостные стены. Древние греки построили мощеную рампу Диолкос длиной 6 км (3,7 мили) , чтобы перетаскивать корабли по суше через Коринфский перешеек . ^[4]

Однако наклонная плоскость была последней из шести классических простых машин, признанной машиной. Вероятно, это связано с тем, что это пассивное и неподвижное устройство (нагрузка – движущаяся часть), ^[21]а еще потому, что он встречается в природе в виде склонов и холмов. Хотя они понимали его использование для подъема тяжелых предметов, древнегреческие философы, давшие определение остальным пяти простым машинам, не включали наклонную плоскость в число машин. ^[22]Эта точка зрения сохранялась среди некоторых более поздних ученых; еще в 1826 году Карл фон Лангсдорф писал, что наклонная плоскость « …не более машина, чем склон горы ». ^[21] Задача вычисления силы, необходимой для поднятия груза по наклонной плоскости (его механическое преимущество), была предпринята греческими философами Героном Александрийским (ок. 10–60 н. э.) и Паппом Александрийским (ок. 290–350 н. э.), но их решения были неверными. ^[23]^[24]^[25]

Лишь в эпоху Возрождения наклонная плоскость была решена математически и отнесена к другим простым машинам. Первый правильный анализ наклонной плоскости появился в работе автора 13 века Иордана де Немора , ^[26]^[27] однако его решение, по-видимому, не было сообщено другим философам того времени. ^[24] Джироламо Кардано (1570) предложил неправильное решение, заключающееся в том, что входная сила пропорциональна углу плоскости. ^[10] Затем, в конце 16 века, в течение десяти лет были опубликованы три правильных решения: Михаилом Варро (1584 г.), Симоном Стевином (1586 г.) и Галилео Галилеем (1592 г.). ^[24] Хотя это было не первое изобретение фламандского инженера Саймона Стевина. ^[25] является наиболее известным из-за своей оригинальности и использования нитки бус (см. Вставку). ^[12]^[26] В 1600 году итальянский ученый Галилео Галилей включил наклонную плоскость в свой анализ простых машин в книге « Le Meccaniche » («О механике»), показав ее основное сходство с другими машинами в качестве усилителя силы. ^[28]

Первые элементарные правила трения скольжения по наклонной плоскости были открыты Леонардо да Винчи (1452-1519), но остались неопубликованными в его записных книжках. ^[29] Они были заново открыты Гийомом Амонтоном (1699 г.) и получили дальнейшее развитие Шарля-Огюстена де Кулона (1785 г.). ^[29] Леонард Эйлер (1750) показал, что тангенс угла естественного откоса на наклонной плоскости равен коэффициенту трения . ^[30]

Терминология [ править ]

Наклон [ править ]

Механическое преимущество наклонной плоскости зависит от ее наклона , то есть уклона или крутизны. Чем меньше уклон, тем больше механическое преимущество и тем меньше сила, необходимая для поднятия заданного веса. Наклон плоскости s равен разнице высот между двумя ее концами, или « подъемом », деленной на ее горизонтальную длину, или « пробег ». ^[31] Его также можно выразить углом, образующим плоскость с горизонтом: $\theta$ .

\theta =\tan ^{-1}{\bigg (}{\frac {\text{Rise}}{\text{Run}}}{\bigg )}\,

Механическое преимущество [ править ]

Механическое преимущество $\mathrm {MA}$ простой машины определяется как отношение выходной силы, действующей на нагрузку, к приложенной входной силе. Для наклонной плоскости выходная сила нагрузки представляет собой просто силу гравитации объекта нагрузки на плоскости, его вес $F_{\text{w}}$ . Входная сила – это сила $F_{\text{i}}$ приложенная к объекту параллельно плоскости, для перемещения его вверх по плоскости. Механическое преимущество заключается в

\mathrm {MA} ={\frac {F_{\text{w}}}{F_{\text{i}}}}\,

The $\mathrm {MA}$ идеальную наклонную плоскость без трения иногда называют идеальным механическим преимуществом. $\mathrm {IMA}$ тогда как MA с учетом трения называется фактическим механическим преимуществом. $\mathrm {AMA}$ . ^[32]

Наклонная плоскость без трения [ править ]

Если между перемещаемым предметом и плоскостью нет трения , то устройство называется идеальной наклонной плоскостью . Это условие может быть достигнуто, если объект катится как бочка или поддерживается на колесах или роликах . Ввиду сохранения энергии для наклонной плоскости без трения работа , совершаемая грузом, поднимающим ее, равна $W_{\text{out}}$ , равен работе, совершаемой приложенной силой, $W_{\text{in}}$ ^[33]^[34]^[35]

W_{\rm {out}}=W_{\rm {in}}\,

Работа определяется как сила, умноженная на перемещение объекта. Работа, совершаемая над грузом, равна его весу, умноженному на вертикальное перемещение, которое он поднимает, что представляет собой «подъем» наклонной плоскости.

W_{\rm {out}}=F_{\rm {w}}\cdot {\text{Rise}}\,

Входная работа равна силе $F_{\text{i}}$ на объекте, умноженное на длину диагонали наклонной плоскости.

W_{\rm {in}}=F_{\rm {i}}\cdot {\text{Length}}\,

Подставляя эти значения в приведенное выше уравнение сохранения энергии и переставляя

{\text{MA}}={\frac {F_{\rm {w}}}{F_{\rm {i}}}}={\frac {\text{Length}}{\text{Rise}}}\,

Чтобы выразить механическое преимущество через угол $\theta$ самолета, ^[34] видно, из диаграммы (вверху) что

\sin \theta ={\frac {\text{Rise}}{\text{Length}}}\,

Так

{\text{MA}}={\frac {F_{\rm {w}}}{F_{\rm {i}}}}={\frac {1}{\sin \theta }}\,

Таким образом, механическое преимущество наклонной плоскости без трения равно обратной величине синуса угла наклона. Входная сила $F_{\rm {i}}$ Из этого уравнения выводится сила, необходимая для того, чтобы удерживать груз неподвижно на наклонной плоскости или толкать его вверх с постоянной скоростью. Если входная сила больше этого значения, нагрузка ускорит самолет. Если сила меньше, он будет ускоряться вниз по самолету.

Наклонная плоскость с трением [ править ]

Там, где между самолетом и грузом существует трение , как, например, когда тяжелый ящик скользит вверх по пандусу, часть работы, приложенной прилагаемой силой, рассеивается в виде тепла за счет трения. $W_{\text{fric}}$ , поэтому над нагрузкой выполняется меньше работы. Благодаря сохранению энергии сумма выходной работы и потерь энергии на трение равна входной работе.

W_{\text{in}}=W_{\text{fric}}+W_{\text{out}}\,

Следовательно, требуется большая входная сила, а механическое преимущество ниже, чем если бы трение отсутствовало. При трении груз будет двигаться только в том случае, если результирующая сила, параллельная поверхности, больше силы трения. $F_{\text{f}}$ выступая против этого. ^[8]^[36]^[37] Максимальная сила трения определяется выражением

F_{f}=\mu F_{n}\,

где $F_{\text{n}}$ - нормальная сила между нагрузкой и плоскостью, направленная нормально к поверхности, и $\mu$ — коэффициент статического трения между двумя поверхностями, который варьируется в зависимости от материала. Если входная сила не приложена, если угол наклона $\theta$ плоскости меньше некоторого максимального значения $\phi$ составляющая гравитационной силы, параллельная плоскости, будет слишком мала, чтобы преодолеть трение, и груз останется неподвижным. Этот угол называется углом естественного откоса и зависит от состава поверхностей, но не зависит от веса груза. Ниже показано, что тангенс угла естественного откоса $\phi$ равно $\mu$

\phi =\tan ^{-1}\mu \,

При трении всегда существует некоторый диапазон входной силы. $F_{\text{i}}$ для которого нагрузка является стационарной, не скользя ни вверх, ни вниз по плоскости, тогда как в случае наклонной плоскости без трения существует только одно конкретное значение входной силы, при котором нагрузка является стационарной.

Анализ [ править ]

На груз, лежащий на наклонной плоскости, если рассматривать его как свободное тело, на него действуют три силы: ^[8]^[36]^[37]

Приложенная сила, $F_{\text{i}}$ приложенная к его перемещению нагрузка, действующая параллельно наклонной плоскости.
Вес груза, $F_{\text{w}}$ , который действует вертикально вниз
Сила самолета на нагрузку. Эту проблему можно разделить на две составляющие:
- Нормальная сила $F_{\text{n}}$ наклонной плоскости на груз, поддерживающий его. Оно направлено перпендикулярно ( нормально ) к поверхности.
- Сила трения, $F_{\text{f}}$ плоскости на нагрузку действует параллельно поверхности и всегда направлена в сторону, противоположную движению объекта. Она равна нормальной силе, умноженной на коэффициент статического трения μ между двумя поверхностями.

Согласно второму закону Ньютона, груз будет находиться в стационарном или установившемся движении, если сумма действующих на него сил равна нулю. Поскольку направление силы трения противоположно для случая движения вверх и вниз, эти два случая необходимо рассматривать отдельно:

Движение вверх: общая сила, действующая на груз, направлена к стороне подъема, поэтому сила трения направлена вниз по плоскости, противодействуя входной силе.

Получение механического преимущества при движении в гору The equilibrium equations for forces parallel and perpendicular to the plane are $\sum F_{\\|}=F_{i}-F_{f}-F_{w}\sin \theta =0\,$ $\sum F_{\perp }=F_{n}-F_{w}\cos \theta =0\,$ Substituting $F_{f}=\mu F_{n}\,$ into first equation $F_{i}-\mu F_{n}-F_{w}\sin \theta =0\,$ Solving second equation to get $F_{n}=F_{w}\cos \theta \,$ and substituting into the above equation $F_{i}-\mu F_{w}\cos \theta -F_{w}\sin \theta =0\,$ ${\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta +\mu \cos \theta }}\,$ Defining $\mu =\tan \phi \,$ ${\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta +\tan \phi \cos \theta }}={\dfrac {1}{\sin \theta +{\dfrac {\sin \phi }{\cos \phi }}\cos \theta }}={\frac {\cos \phi }{\sin \theta \cos \phi +\cos \theta \sin \phi }}\,$ Using a sum-of-angles trigonometric identity on the denominator,

Механическое преимущество заключается в

\mathrm {MA} ={\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin(\theta +\phi )}}\,

где

\phi =\tan ^{-1}\mu \,

. Это условие надвигающегося движения вверх по наклонной плоскости. Если приложенная сила F _i больше, чем указано в этом уравнении, груз переместится вверх по плоскости.

Движение под гору: общая сила, действующая на груз, направлена в сторону спуска, поэтому сила трения направлена вверх по плоскости.

Получение механического преимущества при движении под уклон The equilibrium equations are $\sum F_{\\|}=F_{i}+F_{f}-F_{w}\sin \theta =0\,$ $\sum F_{\perp }=F_{n}-F_{w}\cos \theta =0\,$ Substituting $F_{f}=\mu F_{n}\,$ into first equation $F_{i}+\mu F_{n}-F_{w}\sin \theta =0\,$ Solving second equation to get $F_{n}=F_{w}\cos \theta \,$ and substituting into the above equation $F_{i}+\mu F_{w}\cos \theta -F_{w}\sin \theta =0\,$ ${\frac {F_{w}}{F_{i}}}={\frac {1}{\sin \theta -\mu \cos \theta }}\,$ Substituting in $\mu =\tan \phi \,$ and simplifying as above ${\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin \theta \cos \phi -\cos \theta \sin \phi }}\,$ Using another trigonometric identity on the denominator,

Механическое преимущество заключается в

\mathrm {MA} ={\frac {F_{w}}{F_{i}}}={\frac {\cos \phi }{\sin(\theta -\phi )}}\,

Это условие неизбежного движения вниз по плоскости; если приложенная сила F _i меньше, чем указано в этом уравнении, груз будет скользить по плоскости. Есть три случая:

$\theta <\phi \,$ : Механическое преимущество отрицательное. В отсутствие приложенной силы груз останется неподвижным, и для его скольжения вниз потребуется некоторая отрицательная (нисходящая) сила.
$\theta =\phi \,$ : « Угол откоса ». Механическое преимущество безгранично. Без приложенной силы груз не будет скользить, но малейшая отрицательная сила (вниз по склону) заставит его скользить.
$\theta >\phi \,$ : Механическое преимущество положительное. В отсутствие приложенной силы груз будет скользить вниз по плоскости, и для его удержания в неподвижном состоянии требуется некоторая положительная (подъемная) сила.

Механическое преимущество силы счет за

Механическое преимущество наклонной плоскости заключается в соотношении веса груза на пандусе к силе, необходимой для его подъема по пандусу. Если энергия не рассеивается и не накапливается при движении груза, то это механическое преимущество можно рассчитать, исходя из размеров пандуса.

Чтобы показать это, пусть положение r железнодорожного вагона на пандусе с углом θ над горизонтом задается формулой

\mathbf {r} =R(\cos \theta ,\sin \theta ),

где R – расстояние по пандусу. Теперь скорость автомобиля на пандусе равна

\mathbf {v} =V(\cos \theta ,\sin \theta ).

Поскольку потерь нет, мощность, используемая силой F для перемещения груза вверх по пандусу, равна выходной мощности, которая представляет собой вертикальный подъем веса W. груза

Входная мощность, тянущая автомобиль вверх по пандусу, определяется выражением

P_{\mathrm {in} }=FV,\!

и выходная мощность

P_{\mathrm {out} }=\mathbf {W} \cdot \mathbf {v} =(0,W)\cdot V(\cos \theta ,\sin \theta )=WV\sin \theta .

Приравняйте входную мощность к выходной мощности, чтобы получить механическое преимущество, как

\mathrm {MA} ={\frac {W}{F}}={\frac {1}{\sin \theta }}.

Механическое преимущество наклонной плоскости также можно рассчитать по отношению длины пандуса L к его высоте H, поскольку синус угла пандуса определяется выражением

\sin \theta ={\frac {H}{L}},

поэтому,

\mathrm {MA} ={\frac {W}{F}}={\frac {L}{H}}.

Пример: Если высота пандуса H = 1 метр, а его длина L = 5 метров, то механическое преимущество равно

\mathrm {MA} ={\frac {W}{F}}=5,

это означает, что сила в 20 фунтов поднимет груз массой 100 фунтов.

Наклонная плоскость Liverpool Minard имеет размеры 1804 х 37,50 метра, что обеспечивает механическое преимущество:

\mathrm {MA} ={\frac {W}{F}}=1804/37.50=48.1,

таким образом, сила натяжения троса в 100 фунтов поднимет груз массой 4810 фунтов. Степень этого наклона составляет 2%, что означает, что угол θ достаточно мал, чтобы sin θ≈tan θ.

См. также [ править ]

Ссылки [ править ]

^ Перейти обратно: ^а ^б Коул, Мэтью (2005). Исследуйте науку, 2-е изд . Пирсон Образование. п. 178. ИСБН 978-981-06-2002-8 .
^ Университетский словарь Мерриам-Вебстера, 11-е изд . Мерриам-Вебстер. 2003. С. 629 . ISBN 978-0-87779-809-5 . словарь определений наклонной плоскости.
^ Перейти обратно: ^а ^б ^с ^д «Наклонная плоскость» . Центр математической и естественнонаучной деятельности . Едининформатика. 1999 . Проверено 11 марта 2012 г.
^ Перейти обратно: ^а ^б ^с Сильверман, Баффи (2009). Простые машины: силы в действии, 4-е изд . США: Класс Хайнемана-Рейнтри. п. 7. ISBN 978-1-4329-2317-4 .
^ Перейти обратно: ^а ^б ^с Ортлеб, Эдвард П.; Ричард Кэдис (1993). Машины и работа . Лоренц Образовательная Пресса. стр. iv. ISBN 978-1-55863-060-4 .
^ Перейти обратно: ^а ^б Рейли, Трэвис (24 ноября 2011 г.). «Урок 04: Скольжение вправо по наклонной плоскости» . Преподавайте инженерное дело . Инженерный колледж, Univ. Колорадо в Боулдере. Архивировано из оригинала 8 мая 2012 года . Проверено 8 сентября 2012 г.
^ Скотт, Джон С. (1993). Словарь гражданского строительства . Чепмен и Хилл. п. 14. ISBN 978-0-412-98421-1 . угол трения [механ.] при изучении тел, скользящих по плоским поверхностям, угол между перпендикуляром к поверхности и равнодействующей силой (между телом и поверхностью), когда тело начинает скользить. угол естественного откоса [см] для любого данного сыпучего материала - самый крутой угол к горизонту, при котором поверхность с навалом будет стоять в установленных условиях.
^ Перейти обратно: ^а ^б ^с ^д Амбекар, АГ (2007). Теория механизма и машин . Обучение PHI. п. 446. ИСБН 978-81-203-3134-1 . Угол естественного откоса — предельный угол наклона плоскости, при котором тело, помещенное на наклонную плоскость, только начинает скользить по плоскости.
^ Розен, Джо; Лиза Куинн Готард (2009). Энциклопедия физических наук, том 1 . Издательство информационной базы. п. 375. ИСБН 978-0-8160-7011-4 .
^ Перейти обратно: ^а ^б ^с Коэтсьер, Теун (2010). «Саймон Стевин и возникновение архимедовой механики в эпоху Возрождения» . Гений Архимеда – 23 века влияния на математику, науку и технику: материалы международной конференции, состоявшейся в Сиракузах, Италия, 8–10 июня 2010 г. Спрингер. стр. 94–99. ISBN 978-90-481-9090-4 .
^ Девриз, Йозеф Т.; Гвидо Ванден Берге (2008). «Магия — это не волшебство»: чудесный мир Саймона Стевина . ВИТ Пресс. стр. 136–139. ISBN 978-1-84564-391-1 .
^ Перейти обратно: ^а ^б Фейнман, Ричард П.; Роберт Б. Лейтон; Мэтью Сэндс (1963). Фейнмановские лекции по физике, Vol. Я. США: Калифорнийский институт. технологии. стр. 4.4–4.5. ISBN 978-0-465-02493-3 .
^ EJDijksterhuis: Саймон Стевин, 1943 г.
^ Тереза МакГуайр, Свет на священных камнях , в Конн, Мари А.; Тереза Бенедикт Макгуайр (2007). Не запечатлено в камне: очерки о ритуальной памяти, душе и обществе . Университетское издательство Америки. п. 23. ISBN 978-0-7618-3702-2 .
^ Датч, Стивен (1999). «Догреческие достижения» . Наследие Древнего мира . Страница профессора Стива Датча, Univ. Висконсин в Грин Бэй. Архивировано из оригинала 21 августа 2016 года . Проверено 13 марта 2012 г.
^ Моффетт, Мэриан; Майкл В. Фасио; Лоуренс Вудхаус (2003). Всемирная история архитектуры . Издательство Лоуренса Кинга. п. 9. ISBN 978-1-85669-371-4 .
^ Пит, Т. Эрик (2006). Памятники из грубого камня и их строители . Библиотека Эхо. стр. 11–12. ISBN 978-1-4068-2203-8 .
^ Томас, Берк (2005). «Транспорт и наклонная плоскость» . Строительство пирамид Гизы . world-mysteries.com. Архивировано из оригинала 13 марта 2012 года . Проверено 10 марта 2012 г.
^ Ислер, Мартин (2001). Палки, камни и тени: строительство египетских пирамид . США: Университет Оклахомы Пресс. стр. 211–216 . ISBN 978-0-8061-3342-3 .
^ Спрэг де Камп, Л. (1990). Древние инженеры . США: Барнс и Нобл. п. 43. ИСБН 978-0-88029-456-0 .
^ Перейти обратно: ^а ^б Карл фон Лангсдорф (1826) Машиноведение , цитируется в Рело, Франц (1876). Кинематика машин: Очерки теории машин . Макмиллан. стр. 604 .
^ например, списки простых машин, оставленные римским архитектором Витрувием (ок. 80–15 до н.э.) и греческим философом Героном Александрийским (ок. 10–70 н.э.), состоят из пяти классических простых машин, исключая наклонную плоскость. – Смит, Уильям (1848). Словарь греческих и римских древностей . Лондон: Уолтон и Маберли; Джон Мюррей. п. 722. , Ашер, Эбботт Пейсон (1988). История механических изобретений . США: Courier Dover Publications. стр. 98, 120. ISBN. 978-0-486-25593-4 .
^ Хит, Томас Литтл (1921). История греческой математики, Vol. 2 . Великобритания: Кларендон Пресс. стр. 349 , 433–434.
^ Перейти обратно: ^а ^б ^с Эджидио Феста и Софи Ру , Загадка наклонной плоскости в Лэрд, Уолтер Рой; Софи Ру (2008). Механика и натурфилософия до научной революции . США: Спрингер. стр. 195–221. ISBN 978-1-4020-5966-7 .
^ Перейти обратно: ^а ^б Мели, Доменико Бертолони (2006). Мышление объектами: трансформация механики в семнадцатом веке . Джу Пресс. стр. 35–39. ISBN 978-0-8018-8426-9 .
^ Перейти обратно: ^а ^б Бойер, Карл Б.; Ута К. Мерцбах (2010). История математики, 3-е изд . Джон Уайли и сыновья. ISBN 978-0-470-63056-3 .
^ Ашер, Эбботт Пейсон (1988). История механических изобретений . Публикации Курьера Дувра. п. 106. ИСБН 978-0-486-25593-4 .
^ Мачамер, Питер К. (1998). Кембриджский компаньон Галилея . Лондон: Издательство Кембриджского университета. стр. 47–48. ISBN 978-0-521-58841-6 .
^ Перейти обратно: ^а ^б Армстронг-Элуври, Брайан (1991). Управление машинами с трением . США: Спрингер. п. 10. ISBN 978-0-7923-9133-3 .
^ Мейер, Эрнст (2002). Нанонаука: трение и реология в нанометровом масштабе . Всемирная научная. п. 7. ISBN 978-981-238-062-3 .
^ Перейти обратно: ^а ^б Хэндли, Бретт; Дэвид М. Маршалл; Крейг Кун (2011). Принципы инженерии . Cengage Обучение. стр. 71–73. ISBN 978-1-4354-2836-2 .
^ Деннис, Джонни Т. (2003). Полный справочник идиота по физике . Пингвин. стр. 116–117. ISBN 978-1-59257-081-2 .
^ Нейв, Карл Р. (2010). «Наклон» . Гиперфизика . Кафедра физики и астрономии, Университет штата Джорджия . Проверено 8 сентября 2012 г.
^ Перейти обратно: ^а ^б Мартин, Лори (2010). «Lab Mech14: Наклонная плоскость — простая машина» (PDF) . Наука в движении . Вестминстерский колледж . Проверено 8 сентября 2012 г.
^ Пирсон (2009). Класс физики 10 — Серия The IIT Foundation . Нью-Дели: Pearson Education India. п. 69. ИСБН 978-81-317-2843-7 .
^ Перейти обратно: ^а ^б Бансал, РК (2005). Инженерная механика и сопротивление материалов . Публикации Лакшми. стр. 165–167. ISBN 978-81-7008-094-7 .
^ Перейти обратно: ^а ^б Это приводит к несколько более общим уравнениям, которые охватывают силу, приложенную под любым углом: Гуджрал, И.С. (2008). Инженерная механика . Брандмауэр Медиа. стр. 275–277. ISBN 978-81-318-0295-3 .

Внешние ссылки [ править ]

Интерактивное моделирование наклонной плоскости по физике.

[Cole-1] Перейти обратно: ^а ^б Коул, Мэтью (2005). Исследуйте науку, 2-е изд . Пирсон Образование. п. 178. ИСБН 978-981-06-2002-8 .

[2] Университетский словарь Мерриам-Вебстера, 11-е изд . Мерриам-Вебстер. 2003. С. 629 . ISBN 978-0-87779-809-5 . словарь определений наклонной плоскости.

[Edinformatics-3] Перейти обратно: ^а ^б ^с ^д «Наклонная плоскость» . Центр математической и естественнонаучной деятельности . Едининформатика. 1999 . Проверено 11 марта 2012 г.

[Silverman-4] Перейти обратно: ^а ^б ^с Сильверман, Баффи (2009). Простые машины: силы в действии, 4-е изд . США: Класс Хайнемана-Рейнтри. п. 7. ISBN 978-1-4329-2317-4 .

[Ortleb-5] Перейти обратно: ^а ^б ^с Ортлеб, Эдвард П.; Ричард Кэдис (1993). Машины и работа . Лоренц Образовательная Пресса. стр. iv. ISBN 978-1-55863-060-4 .

[TeachEngineering-6] Перейти обратно: ^а ^б Рейли, Трэвис (24 ноября 2011 г.). «Урок 04: Скольжение вправо по наклонной плоскости» . Преподавайте инженерное дело . Инженерный колледж, Univ. Колорадо в Боулдере. Архивировано из оригинала 8 мая 2012 года . Проверено 8 сентября 2012 г.

[7] Скотт, Джон С. (1993). Словарь гражданского строительства . Чепмен и Хилл. п. 14. ISBN 978-0-412-98421-1 . угол трения [механ.] при изучении тел, скользящих по плоским поверхностям, угол между перпендикуляром к поверхности и равнодействующей силой (между телом и поверхностью), когда тело начинает скользить. угол естественного откоса [см] для любого данного сыпучего материала - самый крутой угол к горизонту, при котором поверхность с навалом будет стоять в установленных условиях.

[Ambekar-8] Перейти обратно: ^а ^б ^с ^д Амбекар, АГ (2007). Теория механизма и машин . Обучение PHI. п. 446. ИСБН 978-81-203-3134-1 . Угол естественного откоса — предельный угол наклона плоскости, при котором тело, помещенное на наклонную плоскость, только начинает скользить по плоскости.

[Rosen-9] Розен, Джо; Лиза Куинн Готард (2009). Энциклопедия физических наук, том 1 . Издательство информационной базы. п. 375. ИСБН 978-0-8160-7011-4 .

[Koetsier-10] Перейти обратно: ^а ^б ^с Коэтсьер, Теун (2010). «Саймон Стевин и возникновение архимедовой механики в эпоху Возрождения» . Гений Архимеда – 23 века влияния на математику, науку и технику: материалы международной конференции, состоявшейся в Сиракузах, Италия, 8–10 июня 2010 г. Спрингер. стр. 94–99. ISBN 978-90-481-9090-4 .

[Devreese-11] Девриз, Йозеф Т.; Гвидо Ванден Берге (2008). «Магия — это не волшебство»: чудесный мир Саймона Стевина . ВИТ Пресс. стр. 136–139. ISBN 978-1-84564-391-1 .

[Feynman-12] Перейти обратно: ^а ^б Фейнман, Ричард П.; Роберт Б. Лейтон; Мэтью Сэндс (1963). Фейнмановские лекции по физике, Vol. Я. США: Калифорнийский институт. технологии. стр. 4.4–4.5. ISBN 978-0-465-02493-3 .

[13] EJDijksterhuis: Саймон Стевин, 1943 г.

[Conn-14] Тереза МакГуайр, Свет на священных камнях , в Конн, Мари А.; Тереза Бенедикт Макгуайр (2007). Не запечатлено в камне: очерки о ритуальной памяти, душе и обществе . Университетское издательство Америки. п. 23. ISBN 978-0-7618-3702-2 .

[Dutch-15] Датч, Стивен (1999). «Догреческие достижения» . Наследие Древнего мира . Страница профессора Стива Датча, Univ. Висконсин в Грин Бэй. Архивировано из оригинала 21 августа 2016 года . Проверено 13 марта 2012 г.

[Moffett-16] Моффетт, Мэриан; Майкл В. Фасио; Лоуренс Вудхаус (2003). Всемирная история архитектуры . Издательство Лоуренса Кинга. п. 9. ISBN 978-1-85669-371-4 .

[Peet-17] Пит, Т. Эрик (2006). Памятники из грубого камня и их строители . Библиотека Эхо. стр. 11–12. ISBN 978-1-4068-2203-8 .

[Thomas-18] Томас, Берк (2005). «Транспорт и наклонная плоскость» . Строительство пирамид Гизы . world-mysteries.com. Архивировано из оригинала 13 марта 2012 года . Проверено 10 марта 2012 г.

[Isler-19] Ислер, Мартин (2001). Палки, камни и тени: строительство египетских пирамид . США: Университет Оклахомы Пресс. стр. 211–216 . ISBN 978-0-8061-3342-3 .

[SpragueDeCamp-20] Спрэг де Камп, Л. (1990). Древние инженеры . США: Барнс и Нобл. п. 43. ИСБН 978-0-88029-456-0 .

[Reuleaux-21] Перейти обратно: ^а ^б Карл фон Лангсдорф (1826) Машиноведение , цитируется в Рело, Франц (1876). Кинематика машин: Очерки теории машин . Макмиллан. стр. 604 .

[22] например, списки простых машин, оставленные римским архитектором Витрувием (ок. 80–15 до н.э.) и греческим философом Героном Александрийским (ок. 10–70 н.э.), состоят из пяти классических простых машин, исключая наклонную плоскость. – Смит, Уильям (1848). Словарь греческих и римских древностей . Лондон: Уолтон и Маберли; Джон Мюррей. п. 722. , Ашер, Эбботт Пейсон (1988). История механических изобретений . США: Courier Dover Publications. стр. 98, 120. ISBN. 978-0-486-25593-4 .

[23] Хит, Томас Литтл (1921). История греческой математики, Vol. 2 . Великобритания: Кларендон Пресс. стр. 349 , 433–434.

[Laird-24] Перейти обратно: ^а ^б ^с Эджидио Феста и Софи Ру , Загадка наклонной плоскости в Лэрд, Уолтер Рой; Софи Ру (2008). Механика и натурфилософия до научной революции . США: Спрингер. стр. 195–221. ISBN 978-1-4020-5966-7 .

[Meli-25] Перейти обратно: ^а ^б Мели, Доменико Бертолони (2006). Мышление объектами: трансформация механики в семнадцатом веке . Джу Пресс. стр. 35–39. ISBN 978-0-8018-8426-9 .

[Boyer-26] Перейти обратно: ^а ^б Бойер, Карл Б.; Ута К. Мерцбах (2010). История математики, 3-е изд . Джон Уайли и сыновья. ISBN 978-0-470-63056-3 .

[Usher-27] Ашер, Эбботт Пейсон (1988). История механических изобретений . Публикации Курьера Дувра. п. 106. ИСБН 978-0-486-25593-4 .

[Machamer-28] Мачамер, Питер К. (1998). Кембриджский компаньон Галилея . Лондон: Издательство Кембриджского университета. стр. 47–48. ISBN 978-0-521-58841-6 .

[Armstrong-29] Перейти обратно: ^а ^б Армстронг-Элуври, Брайан (1991). Управление машинами с трением . США: Спрингер. п. 10. ISBN 978-0-7923-9133-3 .

[Meyer-30] Мейер, Эрнст (2002). Нанонаука: трение и реология в нанометровом масштабе . Всемирная научная. п. 7. ISBN 978-981-238-062-3 .

[Handley-31] Перейти обратно: ^а ^б Хэндли, Бретт; Дэвид М. Маршалл; Крейг Кун (2011). Принципы инженерии . Cengage Обучение. стр. 71–73. ISBN 978-1-4354-2836-2 .

[Dennis-32] Деннис, Джонни Т. (2003). Полный справочник идиота по физике . Пингвин. стр. 116–117. ISBN 978-1-59257-081-2 .

[Hyperphysics-33] Нейв, Карл Р. (2010). «Наклон» . Гиперфизика . Кафедра физики и астрономии, Университет штата Джорджия . Проверено 8 сентября 2012 г.

[Westminster-34] Перейти обратно: ^а ^б Мартин, Лори (2010). «Lab Mech14: Наклонная плоскость — простая машина» (PDF) . Наука в движении . Вестминстерский колледж . Проверено 8 сентября 2012 г.

[Pearson-35] Пирсон (2009). Класс физики 10 — Серия The IIT Foundation . Нью-Дели: Pearson Education India. п. 69. ИСБН 978-81-317-2843-7 .

[Bansal-36] Перейти обратно: ^а ^б Бансал, РК (2005). Инженерная механика и сопротивление материалов . Публикации Лакшми. стр. 165–167. ISBN 978-81-7008-094-7 .

[Gujral-37] Перейти обратно: ^а ^б Это приводит к несколько более общим уравнениям, которые охватывают силу, приложенную под любым углом: Гуджрал, И.С. (2008). Инженерная механика . Брандмауэр Медиа. стр. 275–277. ISBN 978-81-318-0295-3 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

Базы данных авторитетного контроля
National	France BnF data Germany Israel United States
Other	NARA