Простая машина

Эта статья о концепции в физике. Информацию о независимом лейбле см. в разделе Simple Machines . Информацию о программном обеспечении интернет-форума см. на форуме Simple Machines . Для более широкого освещения этой темы см. «Механизм (инженерия)» .

Шесть классических простых машин

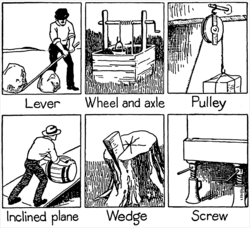
— Простая машина это механическое устройство , изменяющее направление или величину силы . В целом их можно определить как простейшие механизмы, использующие механическое преимущество (также называемое рычагом) для увеличения силы. Обычно этот термин относится к шести классическим простым машинам, которые были определены учеными эпохи Возрождения :

• Рычаг
• Колесо и ось
• Шкив
• Наклонная плоскость
• Клин
• Винт

Простая машина использует одну приложенную силу для выполнения работы против одной силы нагрузки. Если пренебречь потерями на трение , то работа, совершаемая над грузом, равна работе, совершаемой приложенной силой. Машина может увеличить величину выходной силы за счет пропорционального уменьшения расстояния, преодолеваемого грузом. Отношение выходной мощности к приложенной силе называется механическим преимуществом .

Простые машины можно рассматривать как элементарные «строительные блоки», из которых состоят все более сложные машины (иногда называемые «сложными машинами»). ) составлены. используются колеса, рычаги и шкивы Например, в механизме велосипеда . Механическое преимущество сложной машины — это просто продукт механических преимуществ простых машин, из которых она состоит.

Хотя они по-прежнему имеют большое значение в механике и прикладной науке, современная механика вышла за рамки представления о простых машинах как основных строительных блоках, из которых все машины состоят , которое возникло в эпоху Возрождения как неоклассическое расширение древнегреческих текстов. . Огромное разнообразие и сложность современных машинных связей, возникших во время промышленной революции , неадекватно описываются этими шестью простыми категориями. Различные авторы эпохи постренессанса составили расширенные списки «простых машин», часто используя такие термины, как базовые машины , составные машины , или элементы машин , чтобы отличить их от классических простых машин, описанных выше. К концу 1800-х годов Франц Рело идентифицировал сотни элементов машин, назвав их простыми машинами . Современная теория машин рассматривает машины как кинематические цепи , состоящие из элементарных связей, называемых кинематическими парами .

История

Идея простой машины возникла у греческого философа Архимеда примерно в III веке до нашей эры, который изучал простые машины Архимеда : рычаг, шкив и винт . Он открыл принцип механического преимущества рычага. Знаменитое замечание Архимеда относительно рычага: «Дайте мне точку опоры, и я переверну Землю» ( греч . δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω ). выражает свое понимание того, что не существует предела увеличению силы, которого можно достичь, используя механическое преимущество. Позже греческие философы определили пять классических простых машин (исключая наклонную плоскость ) и смогли рассчитать их (идеальное) механическое преимущество. Например, Герон Александрийский ( ок. 10–75 гг. н.э.) в своем труде «Механика» перечисляет пять механизмов, способных «приводить груз в движение»: рычаг , лебедка , шкив , клин и винт , и описывает их изготовление и использование. Однако понимание греков ограничивалось статикой простых машин (балансом сил) и не включало динамику , компромисс между силой и расстоянием или концепцию работы .

В эпоху Возрождения динамику механических сил , как называли простые машины, начали изучать с точки зрения того, насколько далеко они могут поднять груз в дополнение к силе, которую они могут приложить, что в конечном итоге привело к новой концепции механической силы. работа. В 1586 году фламандский инженер Саймон Стевин обнаружил механическое преимущество наклонной плоскости и включил ее в состав других простых машин. Полная динамическая теория простых машин была разработана итальянским ученым Галилео Галилеем в 1600 году в книге Le Meccaniche ( «О механике» ), в которой он показал основное математическое сходство машин как усилителей силы. Он был первым, кто объяснил, что простые машины не создают энергию , а только преобразуют ее.

Классические правила трения скольжения в машинах были открыты Леонардо да Винчи (1452–1519), но не были опубликованы и просто задокументированы в его записных книжках и основывались на доньютоновской науке, например, на убеждении, что трение - это эфирная жидкость. Они были заново открыты Гийомом Амонтоном (1699 г.) и получили дальнейшее развитие Шарля-Огюстена де Кулона (1785 г.).

Идеальная простая машина

Если простая машина не рассеивает энергию за счет трения, износа или деформации, то энергия сохраняется и такая машина называется идеальной простой машиной. В этом случае мощность, поступающая в машину, равна выходной мощности, а механическое преимущество можно рассчитать по ее геометрическим размерам.

Хотя каждая машина работает по-разному механически, их математические функции схожи. В каждой машине есть сила $F_{\text{in}}$ прикладывается к устройству в одной точке, и оно работает , перемещая груз $F_{\text{out}}$ в другой момент. Хотя некоторые машины меняют только направление силы, например неподвижный шкив, большинство машин умножают величину силы на коэффициент, механическое преимущество

$$\mathrm {MA} ={F_{\text{out}} \over F_{\text{in}}}$$

это можно рассчитать на основе геометрии машины и трения.

Простые машины не содержат источника энергии , поэтому они не могут выполнить больше работы , чем получают от входной силы. Простая машина, в которой нет трения и упругости, называется идеальной машиной . Благодаря сохранению энергии в идеальной простой машине выходная мощность (скорость выделения энергии) в любой момент времени $P_{\text{out}}$ равен потребляемой мощности $P_{\text{in}}$

$$P_{\text{out}}=P_{\text{in}}\!$$

Выходная мощность равна скорости нагрузки $v_{\text{out}}\,$ умноженное на силу нагрузки $P_{\text{out}}=F_{\text{out}}v_{\text{out}}\,$. Аналогично, входная мощность приложенной силы равна скорости входной точки. $v_{\text{in}}\,$ умноженное на приложенную силу $P_{\text{in}}=F_{\text{in}}v_{\text{in}}\!$. Поэтому,

$$F_{\text{out}}v_{\text{out}}=F_{\text{in}}v_{\text{in}}\,$$

Итак, механическое преимущество идеальной машины $\mathrm {MA} _{\text{ideal}}\,$ равен отношению скоростей , отношению входной скорости к выходной скорости.

$$\mathrm {MA} _{\text{ideal}}={F_{\text{out}} \over F_{\text{in}}}={v_{\text{in}} \over v_{\text{out}}}\,$$

Отношение скоростей также равно отношению расстояний, пройденных за любой данный период времени.

$${v_{\text{out}} \over v_{\text{in}}}={d_{\text{out}} \over d_{\text{in}}}$$

Следовательно, механическое преимущество идеальной машины также равно отношению расстояния , отношению пройденного входного расстояния к пройденному выходному расстоянию.

$\mathrm {MA} _{\text{ideal}}={F_{\text{out}} \over F_{\text{in}}}={d_{\text{in}} \over d_{\text{out}}}\,$

Это можно рассчитать, исходя из геометрии машины. Например, соотношение механического преимущества и расстояния рычага равно соотношению его плеч .

Механическое преимущество может быть больше или меньше единицы:

• Если $\mathrm {MA} >1\,$, выходная сила больше входной, машина действует как усилитель силы, но расстояние, преодолеваемое нагрузкой $d_{\text{out}}$ меньше расстояния, перемещаемого входной силой $d_{\text{in}}\,$.
• Если $\mathrm {MA} <1\,$, выходная сила меньше входной, но расстояние, преодолеваемое нагрузкой, больше, чем расстояние, преодолеваемое входной силой.

В винте , использующем вращательное движение, входная сила должна быть заменена крутящим моментом , а скорость - угловой скоростью вращения вала.

Трение и эффективность

Все реальные машины имеют трение, из-за которого часть входной мощности рассеивается в виде тепла. Если $P_{\text{fric}}\,$ это мощность, теряемая на трение, из-за сохранения энергии

$$P_{\text{in}}=P_{\text{out}}+P_{\text{fric}}$$

Механический КПД $\eta$ машины (где $0<\eta \ <1$) определяется как отношение выходной мощности к входной мощности и является мерой потерь энергии на трение.

$${\begin{aligned}\eta &\equiv {P_{\text{out}} \over P_{\text{in}}}\\P_{\text{out}}&=\eta P_{\text{in}}\end{aligned}}$$

Как и выше, мощность равна произведению силы и скорости, поэтому

$$F_{\text{out}}v_{\text{out}}=\eta F_{\text{in}}v_{\text{in}}$$

Поэтому,

$\mathrm {MA} ={F_{\text{out}} \over F_{\text{in}}}=\eta {v_{\text{in}} \over v_{\text{out}}}$

Так что в неидеальных машинах механическое преимущество всегда меньше передаточного числа скоростей изделия с КПД $\eta$. Таким образом, машина, в которой присутствует трение, не сможет перемещать такой же большой груз, как соответствующая идеальная машина, используя ту же входную силу.

Составные машины

Сложная машина — это машина, состоящая из набора простых машин, соединенных последовательно, при этом выходная сила одной обеспечивает входную силу для другой. Например, настольные тиски состоят из рычага (ручки тисков), последовательно соединенного с винтом, а простая зубчатая передача состоит из ряда шестерен ( колес и осей ), соединенных последовательно.

Механическое преимущество составной машины представляет собой отношение выходной силы, действующей последней машины в серии, к входной силе, приложенной к первой машине, то есть

$$\mathrm {MA} _{\text{compound}}={F_{{\text{out}}N} \over F_{\text{in1}}}$$

Поскольку выходная сила каждой машины является входной для следующей, $F_{\text{out1}}=F_{\text{in2}},\;F_{\text{out2}}=F_{\text{in3}},\,\ldots \;F_{{\text{out}}K}=F_{{\text{in}}K+1}$, это механическое преимущество также определяется формулой

$$\mathrm {MA} _{\text{compound}}={F_{\text{out1}} \over F_{\text{in1}}}{F_{\text{out2}} \over F_{\text{in2}}}{F_{\text{out3}} \over F_{\text{in3}}}\ldots {F_{{\text{out}}N} \over F_{{\text{in}}N}}\,$$

Таким образом, механическое преимущество сложной машины равно произведению механических преимуществ ряда образующих ее простых машин.

$$\mathrm {MA} _{\text{compound}}=\mathrm {MA} _{1}\mathrm {MA} _{2}\ldots \mathrm {MA} _{N}$$

Точно так же КПД сложной машины также является продуктом КПД ряда простых машин, которые ее образуют.

$$\eta _{\text{compound}}=\eta _{1}\eta _{2}\ldots \;\eta _{N}.$$

Самоблокирующиеся машины

резьбовых таких Свойство самоконтрящегося винта является причиной его широкого использования в соединениях, как болты и шурупы.

Во многих простых машинах, если сила нагрузки $F_{\textrm {out}}$ на машине достаточно высока по отношению к входной силе $F_{\textrm {in}}$, машина будет двигаться назад, при этом сила нагрузки будет совершать работу над входной силой. Таким образом, эти машины можно использовать в любом направлении, при этом движущая сила прикладывается к любой точке входа. Например, если сила нагрузки на рычаг достаточно велика, рычаг переместится назад, перемещая входной рычаг назад против входной силы. Их называют реверсивными , неблокирующими или ремонтными машинами, а движение назад – капитальным .

Однако в некоторых машинах, если силы трения достаточно велики, никакая сила нагрузки не может сдвинуть его назад, даже если входная сила равна нулю. Это называется самоблокирующейся , нереверсивной или неремонтопригодной машиной. Эти машины могут быть приведены в движение только с помощью входной силы, и когда входная сила будет снята, они останутся неподвижными, «заблокированными» трением в каком бы положении они ни находились.

Самоблокировка возникает преимущественно в машинах с большими площадями скользящего контакта между движущимися частями: винтом , наклонной плоскостью и клином :

• Самый распространенный пример – винт. В большинстве винтов приложение крутящего момента к валу может привести к его повороту, линейному перемещению вала для выполнения работы против нагрузки, но никакая осевая нагрузка на вал не заставит его повернуться назад.
• В наклонной плоскости груз может быть подтянут вверх под действием боковой силы, но если плоскость не слишком крутая и между грузом и плоскостью достаточно трения, то при снятии входной силы груз останется неподвижным и будет не скользить по самолету, независимо от его веса.
• Клин можно вбить в деревянный брусок силой на конце, например, ударив по нему кувалдой, раздвигая стороны, но никакая сила сжатия со стороны деревянных стенок не заставит его выскочить обратно из бруса. блокировать.

Машина будет самоблокирующейся тогда и только тогда, когда ее эффективность $\eta$ ниже 50%:

$$\eta \equiv {\frac {F_{\text{out}}/F_{\text{in}}}{d_{\text{in}}/d_{\text{out}}}}<0.5$$

Является ли машина самоблокирующейся, зависит как от сил трения ( коэффициента статического трения ) между ее частями, так и от соотношения расстояний $d_{\textrm {in}}/d_{\textrm {out}}$ (идеальное механическое преимущество). Если и трение, и идеальное механическое преимущество достаточно высоки, он самоблокируется.

Доказательство

Когда машина движется вперед из точки 1 в точку 2, при этом входная сила совершает работу над силой нагрузки, из-за сохранения энергии входная работа $W_{\text{1,2}}$ равна сумме работ, совершенных над силой нагрузки $W_{\text{load}}$ и работа потеряна из-за трения $W_{\text{fric}}$

$W_{\text{1,2}}=W_{\text{load}}+W_{\text{fric}}$ ( Уравнение 1 )

Если КПД ниже 50% ( $\eta =W_{\text{load}}/W_{\text{1,2}}<0.5$):

$$2W_{\text{load}}<W_{\text{1,2}}\,$$

Из уравнения. 1

$${\begin{aligned}2W_{\text{load}}&<W_{\text{load}}+W_{\text{fric}}\\W_{\text{load}}&<W_{\text{fric}}\end{aligned}}$$

Когда машина движется назад из точки 2 в точку 1, при этом сила нагрузки совершает работу над входной силой, работа теряется на трение. $W_{\text{fric}}$ это то же самое

$$W_{\text{load}}=W_{\text{2,1}}+W_{\text{fric}}$$

Таким образом, выходная работа равна

$$W_{\text{2,1}}=W_{\text{load}}-W_{\text{fric}}<0$$

Таким образом, машина самоблокируется, поскольку работа, рассеиваемая на трение, больше, чем работа, совершаемая силой груза, перемещающей ее назад, даже при отсутствии приложенной силы.

Современная теория машин

Машины изучаются как механические системы, состоящие из приводов и механизмов , передающих силы и движение, контролируемых датчиками и контроллерами. Компоненты приводов и механизмов состоят из звеньев и шарниров, образующих кинематические цепи.

Кинематические цепи

Иллюстрация четырехзвенной связи из книги «Кинематика машин», 1876 г.

Простые машины — это элементарные примеры кинематических цепей , которые используются для моделирования механических систем — от парового двигателя до роботов-манипуляторов. Подшипники, которые образуют точку опоры рычага и позволяют вращаться колесу, оси и шкивам, являются примерами кинематической пары , называемой шарнирным соединением. Точно так же плоская поверхность наклонной плоскости и клина являются примерами кинематической пары, называемой скользящим соединением. Винт обычно идентифицируется как отдельная кинематическая пара, называемая винтовым соединением.

Два рычага, или кривошипа, объединяются в плоскую четырехзвенную связь путем присоединения звена, соединяющего выход одного кривошипа со входом другого. Дополнительные звенья могут быть присоединены для образования шестизвенной связи или последовательно для формирования робота.

Классификация машин

Идентификация простых машин возникает из-за стремления к систематическому методу изобретения новых машин. Поэтому важной проблемой является то, как простые машины объединяются в более сложные машины. Один из подходов состоит в том, чтобы соединить простые машины последовательно, чтобы получить сложные машины.

Однако более успешную стратегию нашел Франц Рёло , который собрал и изучил более 800 элементарных машин. Он понял, что рычаг, шкив, колесо и ось — это, по сути, одно и то же устройство: тело, вращающееся вокруг шарнира. Аналогично наклонная плоскость, клин и винт представляют собой брусок, скользящий по плоской поверхности.

Это понимание показывает, что именно суставы или соединения, обеспечивающие движение, являются основными элементами машины. Начиная с четырех типов соединений: вращательного соединения , скользящего соединения , кулачкового соединения и зубчатого соединения , а также связанных с ними соединений, таких как тросы и ремни, можно понимать машину как совокупность твердых частей, которые соединяют эти соединения.

Кинематический синтез

Проектирование механизмов для выполнения необходимого движения и передачи силы известно как кинематический синтез . Это сборник геометрических методов механического проектирования рычажных , кулачковых и ведомых механизмов , а также зубчатых передач и зубчатых передач .

См. также

• Соединение (механическое)
• Кулачковые и следящие механизмы
• Шестерни и зубчатые передачи
• Механизм (инжиниринг)
• Роламит — единственная элементарная машина, открытая в 20 веке.