Соединение (механическое)

В данной статье речь идет о узлах звеньев, предназначенных для управления силами и движением. Чтобы узнать о других целях, см. «Связывание» .

Двигатель с регулируемым ходом поршня (Справочник Autocar, девятое издание)

Механическая связь представляет собой совокупность систем, связанных для управления силами и движением . Движение тела или звена изучается с помощью геометрии , поэтому звено считается жестким . Соединения между звеньями моделируются как обеспечивающие идеальное движение, например чистое вращение или скольжение , и называются соединениями. Связь, моделируемая как сеть жестких звеньев и идеальных соединений, называется кинематической цепью .

Связи могут быть построены из открытых цепей, закрытых цепей или комбинации открытых и закрытых цепей. Каждое звено цепи соединено шарниром с одним или несколькими другими звеньями. Таким образом, кинематическую цепь можно смоделировать как граф, в котором звенья являются путями, а соединения — вершинами, который называется графом связей.

Развертываемое зеркальное соединение состоит из ряда ромбовидных или ножничных рычагов.

Удлиненный ножничный подъемник

Движение идеального сустава обычно связывают с подгруппой группы евклидовых перемещений. Количество параметров в подгруппе называется степенями свободы (ГРИП) соединения.Механические связи обычно предназначены для преобразования заданной входной силы и движения в желаемую выходную силу и движение. Отношение выходной силы к входной силе известно как механическое преимущество рычажного механизма, а отношение входной скорости к выходной скорости известно как передаточное отношение . Передаточное число и механическое преимущество определены таким образом, чтобы в идеальном соединении они давали одинаковое число.

Кинематическая цепь, в которой одно звено неподвижно или неподвижно, называется механизмом. а связь, предназначенная для стационарного использования, называется конструкцией .

История

Архимед прикладная геометрия для изучения рычага. В 1500-х годах работы Архимеда и Героя Александрийского были основными источниками теории машин. Именно Леонардо да Винчи привнес изобретательскую энергию в машины и механизмы.

В середине 1700-х годов значение парового двигателя приобретало все большее значение, и Джеймс Уатт понял, что эффективность можно повысить, используя различные цилиндры для расширения и конденсации пара. Это привело его к поиску механизма, который мог бы преобразовать вращение кривошипа в линейное скольжение, и привело к открытию так называемого механизма Уотта . Это привело к изучению связей, которые могли бы образовывать прямые линии, хотя бы приблизительно; и вдохновил математика Дж. Дж. Сильвестра , который читал лекции о рычаге Поселье , который генерирует точную прямую линию от вращающегося кривошипа.

Работы Сильвестра вдохновили А. Б. Кемпе , который показал, что связи для сложения и умножения можно собрать в систему, описывающую заданную алгебраическую кривую. Процедура проектирования Кемпе вдохновила исследования на стыке геометрии и информатики.

В конце 1800-х годов Ф. Рело , А.Б. Кеннеди и Л. Бурместер формализовали анализ и синтез систем связей с помощью начертательной геометрии , а П. Л. Чебышев ввел аналитические методы исследования и изобретения связей.

В середине 1900-х годов Ф. Фрейденштейн и Г. Н. Шандор использовал недавно разработанный цифровой компьютер для решения уравнений контура связи и определения ее размеров для желаемой функции, начав компьютерное проектирование связей. В течение двух десятилетий эти компьютерные методы стали неотъемлемой частью анализа сложных машинных систем. и управление роботами-манипуляторами.

Р.Э. Кауфман объединили способность компьютера быстро вычислять корни полиномиальных уравнений с графическим пользовательским интерфейсом, чтобы объединить методы Фрейденштайна с геометрическими методами Рело и Бурместера и сформировать KINSYN, интерактивную компьютерную графическую систему для проектирования рычажных механизмов.

Современное исследование связей включает в себя анализ и проектирование шарнирных систем, которые появляются в роботах, станках, а также системах с тросовым приводом и тенсегрити. Эти методы также применяются к биологическим системам и даже к изучению белков.

Мобильность

Простые связи способны производить сложное движение.

Конфигурация системы жестких звеньев, соединенных идеальными соединениями, определяется набором параметров конфигурации, таких как углы вокруг поворотного соединения и скольжения по призматическим соединениям, измеренные между соседними звеньями. Геометрические ограничения связи позволяют рассчитывать все параметры конфигурации с точки зрения минимального набора, который является входными параметрами . Количество входных параметров называется подвижностью или степенью свободы системы рычагов.

Система n твердых тел, движущихся в пространстве, имеет 6n степеней свободы, измеренных относительно неподвижной системы отсчета. Включив эту систему отсчёта в счёт тел, чтобы подвижность не зависела от выбора фиксированной системы отсчёта, тогда имеем M = 6( N − 1), где N = n + 1 — количество движущихся тел плюс неподвижное тело. .

Суставы, соединяющие тела в этой системе, лишают степеней свободы и уменьшают подвижность. В частности, петли и ползунки налагают по пять ограничений и, следовательно, удаляют пять степеней свободы. Удобно определить количество ограничений c , которые накладывает сустав, через свободу соединения f , где c = 6 − f . В случае шарнира или ползунка, которые представляют собой соединения с одной степенью свободы, мы имеем f = 1 и, следовательно, c = 6 - 1 = 5.

Таким образом, подвижность рычажной системы, образованной из n движущихся звеньев и j суставов, каждый из которых имеет f _i , i = 1, ..., j , степени свободы, может быть вычислена как:

$M=6n-\sum _{i=1}^{j}(6-f_{i})=6(N-1-j)+\sum _{i=1}^{j}\ f_{i},$

где N включает фиксированную ссылку. Это известно как уравнение Куцбаха – Грюблера.

Есть два важных особых случая: (i) простая открытая цепь и (ii) простая закрытая цепь. Простая разомкнутая цепь состоит из n подвижных звеньев, соединенных встык j шарнирами, причем один конец соединен с заземляющим звеном. Таким образом, в этом случае N = j + 1 и подвижность цепи равна

$M=\sum _{i=1}^{j}\ f_{i}.$

В простой замкнутой цепи n подвижных звеньев соединены встык с помощью n +1 шарниров так, что два конца соединены с заземляющим звеном, образуя петлю. В этом случае N = j и подвижность цепи равна

$M=\sum _{i=1}^{j}\ f_{i}-6.$

Примером простой открытой цепи является серийный робот-манипулятор. Эти роботизированные системы состоят из ряда звеньев, соединенных шестью вращающимися или призматическими шарнирами с одной степенью свободы, поэтому система имеет шесть степеней свободы.

Примером простой замкнутой цепи является пространственная четырехзвенная связь РССР (оборота-сфера-сфера-оборота). Сумма свобод этих шарниров равна восьми, поэтому подвижность звена равна двум, где одна из степеней свободы представляет собой поворот муфты вокруг линии, соединяющей два S-образных шарнира.

Плоское и сферическое движение

Мобильность связей

Стопорные плоскогубцы представляют собой механическую связь с четырьмя стержнями и одной степенью свободы . с двумя степенями свободы Регулируемый базовый шарнир представляет собой пятизвенную рычажную систему .

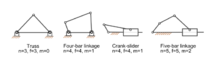
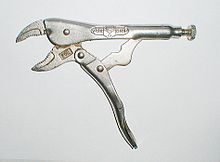
Обычной практикой является проектирование системы рычагов таким образом, чтобы движение всех тел лежало в параллельных плоскостях, образуя так называемую плоскую связь . Также возможно построить систему связей так, что все тела движутся по концентрическим сферам, образуя сферическую связь . В обоих случаях степень свободы связи теперь равна трем, а не шести, а ограничения, налагаемые соединениями, теперь равны c = 3 − f .

В этом случае формула мобильности имеет вид

$M=3(N-1-j)+\sum _{i=1}^{j}\ f_{i},$

и у нас есть особые случаи,

• плоская или сферическая простая открытая цепь,

$M=\sum _{i=1}^{j}\ f_{i},$

• плоская или сферическая простая замкнутая цепь,

$M=\sum _{i=1}^{j}\ f_{i}-3.$

Примером плоской простой замкнутой цепи является плоская четырехзвенная рычажная система, которая представляет собой четырехзвенную петлю с четырьмя шарнирами по одной степени свободы и поэтому имеет подвижность М = 1.

Суставы

Наиболее знакомыми соединениями для систем рычагов являются вращающееся или шарнирное соединение, обозначаемое буквой R, и призматическое , или скользящее, соединение, обозначаемое буквой P. Большинство других соединений, используемых для пространственных связей, моделируются как комбинации вращающихся и призматических соединений. Например,

• цилиндрическое соединение состоит из последовательной цепи RP или PR, построенной так, что оси вращательного и призматического соединений параллельны,
• универсальный шарнир состоит из последовательной цепи RR, сконструированной таким образом, что оси поворотных шарниров пересекаются под углом 90°;
• шаровой шарнир состоит из последовательной цепочки РРР, у которой каждая из осей шарнирного соединения пересекается в одной и той же точке;
• плоское соединение может быть построено как плоская последовательная цепочка RRR, RPR и PPR, имеющая три степени свободы.

Анализ и синтез связей

Основной математический инструмент для анализа связи известен как кинематические уравнения системы. Это последовательность трансформаций твердого тела по последовательной цепи внутри рычажного механизма, который позиционирует плавающее звено относительно наземной рамы. Каждая последовательная цепь в звене, соединяющем это плавающее звено с землей, предоставляет набор уравнений, которым должны удовлетворять параметры конфигурации системы. В результате получается набор нелинейных уравнений, определяющих параметры конфигурации системы для набора значений входных параметров.

Фрейденштайн представил метод использования этих уравнений для расчета плоской четырехзвенной связи для достижения заданного соотношения между входными параметрами и конфигурацией связи. Другой подход к конструкции плоского четырехзвенного механизма был предложен Л. Бурместером и называется теорией Бурместера .

степенью свободы

Формула подвижности позволяет определить количество звеньев и соединений в плоской связи, которая дает связь с одной степенью свободы. Если мы требуем, чтобы подвижность плоской связи была M = 1 и fi _: = 1, результат будет следующим

$M=3(N-1-j)+j=1,\!$

или

$j={\frac {3}{2}}N-2.\!$

Эта формула показывает, что связь должна иметь четное количество связей, поэтому мы имеем

• N = 2, j = 1: это двухзвенная связь, известная как рычаг ;
• N = 4, j = 4: это четырехзвенная связь ;
• N = 6, j = 7: это шестизвенная связь [у нее есть два звена с тремя соединениями, называемые тройными звеньями, и существует две топологии этой связи в зависимости от того, как эти звенья соединены. В топологии Ватта два тройных канала соединены между собой соединением. В топологии Стивенсона два троичных канала соединены двоичными;
• N = 8, j = 10: восьмизвенная связь имеет 16 различных топологий;
• N = 10, j = 13: 10-звенная связь имеет 230 различных топологий,
• N = 12, j = 16: 12-бар имеет 6856 топологий.

См. Сункари и Шмидта. за количество 14- и 16-стержневых топологий, а также количество связей, имеющих две, три и четыре степени свободы.

Плоская четырехзвенная связь, вероятно, является самой простой и распространенной. Это система с одной степенью свободы, которая преобразует вращение входного кривошипа или смещение ползуна в выходное вращение или скольжение.

Примеры четырехзвенных связей:

• кривошип-коромысло, у которого входной кривошип полностью вращается, а выходное звено раскачивается вперед и назад;
• ползун-кривошип, у которого входной кривошип вращается, а выходной ползун перемещается вперед и назад;
• механизмы с перетаскиванием, в которых входной кривошип полностью вращается и тащит выходной кривошип в полностью вращательное движение.

Типы четырехзвенных звеньев с присвоенной каждому звену длиной – обратите внимание на самое короткое звено S и самое длинное звено L каждого из этих механизмов.

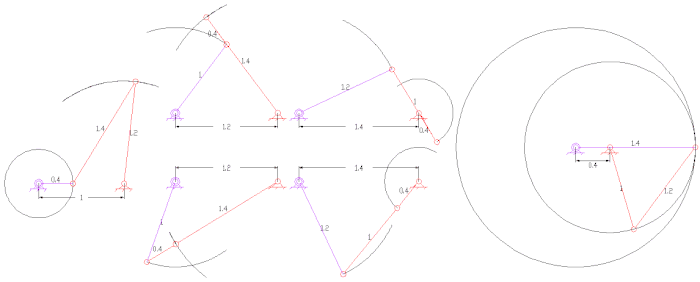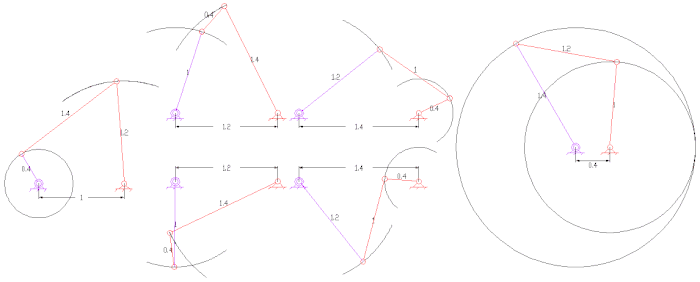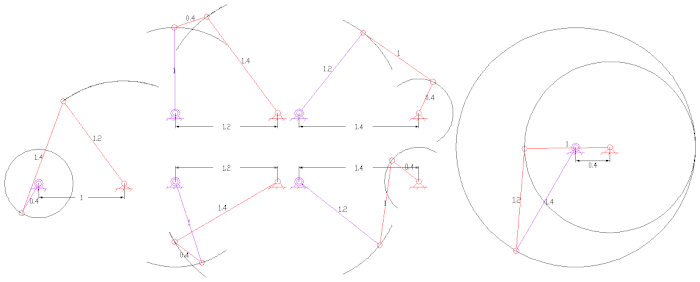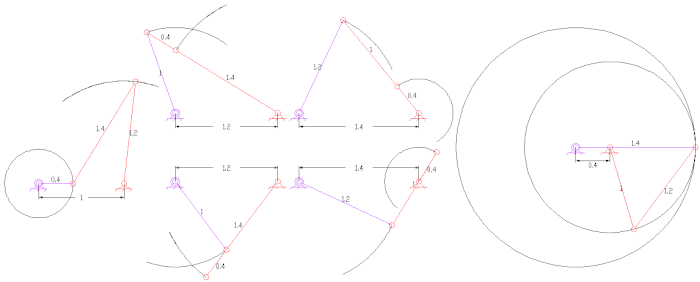
Другие интересные связи

Четырехполосный генератор функций, аппроксимирующий функцию Log(u) для 1 < u < 10.

• Пантограф (четырехполосный, две ГРИП)
• Пять звеньев часто имеют зацепляющиеся шестерни для двух звеньев, образуя рычажок с одной степенью свободы. Они могут обеспечить большую передачу мощности и большую гибкость конструкции, чем четырехзвенные рычажные механизмы.
• Рычаг Янсена представляет собой восьмирычажный механизм на ножках , который был изобретен кинетическим скульптором Тео Янсеном .
• Рычажный механизм Клана представляет собой шестизвенную рычажную систему, образующую ножной механизм ;
• Тумблеры представляют собой четырехрычажные рычаги, размеры которых позволяют их складывать и фиксировать. Положения переключателей определяются коллинеарностью двух движущихся звеньев. Рычажный механизм имеет такие размеры, что рычаг достигает положения переключения непосредственно перед складыванием. Высокое механическое преимущество позволяет входному кривошипу деформировать рычажный механизм ровно настолько, чтобы вытолкнуть его за пределы положения рычага переключения передач. Это фиксирует вход на месте. В качестве зажимов используются коленно-рычажные механизмы.

Прямолинейные механизмы

Основная статья: Прямолинейный механизм

• Джеймса Уотта Параллельное движение и связь Уатта
• Рычаг Поселье-Липкина , первый плоский рычаг, создающий идеальный прямой выходной сигнал при вращении; восьмиполосный, одна ГРИП.
• Рычаг Скотта Рассела , который преобразует линейное движение в (почти) линейное движение по линии, перпендикулярной входному сигналу.
• Рычаг Чебышева , обеспечивающий практически прямолинейное движение стрелы при четырехзвенной навеске.
• Рычаг Хукенса , обеспечивающий почти прямолинейное движение стрелы с помощью четырехрычажного механизма.
• Саррусовая связь , обеспечивающая движение одной поверхности в направлении, нормальном к другой.
• Инвертор Харта , обеспечивающий идеальное прямолинейное движение без скользящих направляющих.

Биологические связи

Системы связей широко распространены у животных. Наиболее подробный обзор различных типов связей у животных был предоставлен Мисом Мюллером. который также разработал новую систему классификации, которая особенно хорошо подходит для биологических систем. Известный пример – крестообразные связки колена.

Важное различие между биологическими и инженерными связями заключается в том, что вращающиеся стержни редки в биологии и что обычно возможен лишь небольшой диапазон теоретически возможных из-за дополнительных функциональных ограничений (особенно необходимости доставки крови). Биологические связи часто соответствуют друг другу . Часто один или несколько стержней образованы связками, и часто связи бывают трехмерными. Известны спаренные рычажные системы, а также пяти-, шести- и даже семизвенные системы. четырехзвенные соединения Однако наиболее распространенными являются .

Связи можно найти в суставах, таких как колено четвероногих . , скакательный сустав овцы и черепной механизм птиц и рептилий Последний отвечает за движение верхней части клюва вверх у многих птиц.

Рычажные механизмы особенно часты и разнообразны в голове костистых рыб , таких как губаны , у которых развилось множество специализированных механизмов питания . Особенно развиты рычажные механизмы выдвижения челюстей . При аспирационном питании система связанных четырехстержневых рычагов отвечает за скоординированное открытие рта и трехмерное расширение полости рта. Другие связи ответственны за выпячивание кости предчелюстной .

Связи также присутствуют в качестве фиксирующих механизмов, например, в колене лошади, что позволяет животному спать стоя, без активного сокращения мышц. При поворотном кормлении , используемом некоторыми костистыми рыбами, четырехстержневой рычажный механизм сначала фиксирует голову в согнутом вентральном положении за счет совмещения двух стержней. При отпускании фиксирующего механизма голова поднимается вверх, а рот перемещается в сторону добычи в течение 5–10 мс.

Галерея изображений

• 
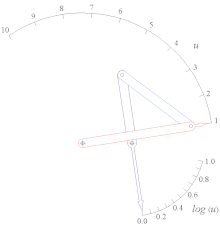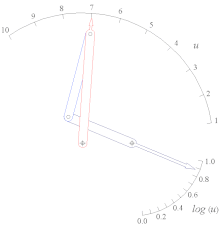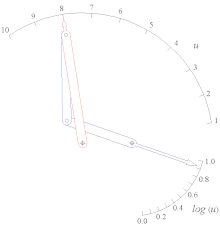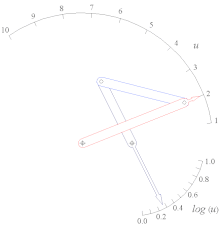
  Генератор функций кулисно-ползункового типа, аппроксимирующий функцию Log(u) для 1 < u < 10.
• 
  Генератор функций ползунка-качалки, аппроксимирующий функцию Tan(u) для 0 < u < 45°.
• 
  Неподвижные и подвижные центроды четырехзвенной рычажной системы.
• 
  Реечная четырехзвенная рычажная система
• 
  механизм РТРТР
• 
  механизм РТРТР
• 
  Шестеренчатые пятизвенные механизмы
• 
  3D кривошипно-ползунковый механизм
• 
  Анимированный персонаж Пиноккио
• 
• 
  Кроуфорда Коникограф
• 
  Раскладной механизм складывания наружу
• 
  Раскладной механизм складывания внутрь

См. также

• Ассур Группы
• Механизм задержки
• Развертываемая структура
• Инженерная механика
• Четырехзвенная связь
• Механический генератор функций
• Кинематика
• Кинематическая муфта
• Кинематическая пара
• Кинематический синтез
• Кинематические модели в Mathcad
• Механизм ног
• Рычаг
• Машина
• Схема машин
• Чрезмерно ограниченный механизм
• Параллельное движение
• Возвратно-поступательное движение
• Слайдер-кривошип
• Трехточечная сцепка

Дальнейшее чтение

• Брайант, Джон; Сангвин, Крис (2008). Насколько круглый ваш круг? : где встречаются инженерия и математика . Принстон: Издательство Принстонского университета. п. 306. ИСБН  978-0-691-13118-4 . — Связь между математическими и реальными механическими моделями, историческое развитие точной обработки, некоторые практические советы по изготовлению физических моделей, с большим количеством иллюстраций и фотографий.
• Эрдман, Артур Г.; Сандор, Джордж Н. (1984). Проектирование механизмов: анализ и синтез . Прентис-Холл. ISBN  0-13-572396-5 .
• Хартенберг, Р.С. и Дж. Денавит (1964) Кинематический синтез связей , Нью-Йорк: McGraw-Hill — Интернет-ссылка из Корнельского университета .
• Кидвелл, Пегги Олдрич ; Эми Акерберг-Гастингс; Дэвид Линдси Робертс (2008). Инструменты американского преподавания математики, 1800–2000 гг . Балтимор: Издательство Университета Джонса Хопкинса. стр. 233–242. ISBN  978-0-8018-8814-4 . - «Связи: своеобразное увлечение» (глава 14) представляет собой обсуждение использования механических связей в американском математическом образовании, включает обширные ссылки.
• Как нарисовать прямую линию - историческое обсуждение конструкции связей в Корнельском университете.
• Пармли, Роберт. (2000). «Раздел 23: Связь». Иллюстрированный справочник по механическим компонентам. Нью-Йорк: МакГроу Хилл. ISBN   0-07-048617-4 Рисунки и обсуждение различных связей.
• Склейтер, Нил. (2011). «Связи: приводы и механизмы». Справочник по механизмам и механическим устройствам. 5-е изд. Нью-Йорк: МакГроу Хилл. стр. 89–129. ISBN   978-0-07-170442-7 . Чертежи и конструкции различных связей.

Внешние ссылки

• Цифровая библиотека кинематических моделей для проектирования (KMODDL) — крупный веб-ресурс по кинематике. Фильмы и фотографии сотен работающих моделей механических систем из коллекции механизмов и машин Рело Корнелльского университета , а также пяти других крупных коллекций. Включает библиотеку электронных книг , содержащую десятки классических текстов по машиностроению и проектированию. Включает модели САПР и стереолитографические файлы для выбранных механизмов.
• Библиотека цифровых механизмов и механизмов (DMG-Lib) (на немецком языке: Digitale Mechanismen- und Getriebebibliothek) — Интернет-библиотека о рычажных механизмах и кулачках (в основном на немецком языке)
• Расчеты связей
• Вводная лекция по связям
• Виртуальные механизмы, анимированные Java
• Аппарат для рисования на основе связей Роберта Хаусара
• (АСОМ) Анализ, синтез и оптимизация многозвенных связей
• Анимация рычажных механизмов на сайте Mechanicaldesign101.com включает плоские и сферические четырех- и шестизвенные рычаги.
• Анимация плоских и сферических четырехзвенных рычагов.
• Анимация связи Беннета.
• Пример генератора функций с шестью полосами, который вычисляет угол места для заданного диапазона.
• Анимации шестирычажной подвески велосипеда.
• Разнообразие конструкций шестизвенных рычагов.
• Введение в связи
• Система моделирования механизма планарной связи и механического синтеза с открытым исходным кодом.