Прямолинейный механизм

Прямолинейный механизм — это механизм , который преобразует любой тип вращательного или углового движения в идеальное или почти идеальное прямолинейное движение или наоборот . Прямолинейное движение — это линейное движение определенной длины или «хода», при котором за каждым ходом вперед следует обратный ход, что дает возвратно-поступательное движение . Первый такой механизм, запатентованный в 1784 году Джеймсом Уоттом , производил приблизительно прямолинейное движение, названное Уаттом параллельным движением .

Прямолинейные механизмы используются в различных приложениях, таких как двигатели, подвески транспортных средств, шагающие роботы и колеса вездеходов. ^{[ нужна ссылка ]}

История

В конце восемнадцатого века, до изобретения строгального и фрезерного станка , было чрезвычайно сложно обрабатывать прямые, плоские поверхности. В то время много внимания уделялось проблеме достижения прямолинейного движения , поскольку это позволило бы обрабатывать плоские поверхности. Чтобы найти решение проблемы, первый прямолинейный механизм разработал Джеймс Уотт для направления поршня первых паровых двигателей. Хотя он и не создает точную прямую линию, хорошее приближение достигается на значительном расстоянии.

Идеальные прямолинейные соединения были обнаружены позже, в девятнадцатом веке, но они не были столь необходимы, поскольку к тому времени были разработаны другие методы механической обработки. ^{[ нужна ссылка ]}

Список связей

Приблизительные прямые связи

В этих механизмах часто используются четырехрычажные тяги, поскольку для них требуется очень мало деталей. Эти четырехзвенные рычаги имеют кривые муфты , которые имеют одну или несколько областей почти идеального прямолинейного движения. Исключением в этом списке является параллельное движение Уатта, которое сочетает в себе рычажное соединение Уотта с другим четырехзвенным рычажным механизмом – пантографом – для усиления существующего приблизительно прямолинейного движения.

Невозможно создать идеально прямолинейное движение с помощью четырехзвенной рычажной системы без использования призматического шарнира .

Связь Ватта (1784 г.)
Параллельное движение Ватта (1784 г.)
Рычаг Эванса "Кузнечик" (1801 г.)
Чебышевская навеска
Чебышевская лямбда-связь (1878 г.) - родственная связь Чебышевской связи.
Связь Робертса
Соединение «лошадь-голова»
Рычажный механизм Hoecken (1926 г.) - требует скользящего соединения.

Идеальные прямые связи

В конечном итоге будет достигнуто идеальное прямолинейное движение.

Связь Саррюса была первой идеальной линейной связью, созданной в 1853 году. Однако это скорее пространственная связь, чем плоская связь. Первое плоское соединение было осуществлено только в 1864 году.

В настоящее время все плоские связи, которые обеспечивают идеальное линейное движение, используют инверсию вокруг круга для создания гипотетического круга бесконечного радиуса, который представляет собой линию. Поэтому их называют инверторами или инверторными ячейками.
Самыми простыми решениями являются W-образная рама Харта, в которой используются 6 стержней, и четырехплоскостные инверторы - Сильвестр-Кемпе и Кумара-Камплинг, в которых также используются 6 стержней.

Рычаг Скотта Рассела (1803 г.) передает линейное движение под прямым углом, но сам по себе не является прямолинейным механизмом. Связь «Луч Кузнечика/Эванса» , приблизительная прямая связь, и связь Брикара, точная прямая связь, имеют общие черты со связью Скотта Рассела и « Траммелю Архимеда» .

Сложные эксцентриковые механизмы с эллиптическим движением

Эти механизмы используют принцип кривой качения вместо кривой муфты и могут преобразовывать непрерывное, а не просто ограниченное вращательное движение в возвратно-поступательное движение и наоборот посредством эллиптического движения. Прямолинейное синусоидальное движение не создает сил инерции второго порядка, что упрощает балансировку в высокоскоростных машинах.

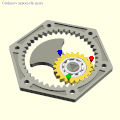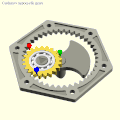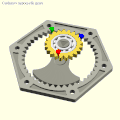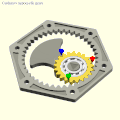
Карданный прямолинейный механизм . Используя принцип пары Туси (1247), прямозубая шестерня вращается внутри кольцевой шестерни с внутренними зубьями , вдвое большего диаметра. Гипоциклоида , очерченная любой точкой делительной окружности меньшего колеса, представляет собой диаметр большего колеса. Этот механизм использовался в гипоциклическом двигателе Мюррея .

Тропа Архимеда . Первоначально эллипсограф. В качестве механизма он использует тот факт, что окружность и прямая линия являются частными случаями эллипса. Он основан во многом на том же кинематическом принципе, что и прямолинейный механизм Кардана (см. выше), и его можно рассматривать как прямозубую шестерню с двумя зубьями в кольцевой шестерне с четырьмя зубьями. Он использовался в двигателе Бейкер-Кросс. ^[3] В перевернутой форме он использовался в паровой машине Парсонса. ^[4] и сегодня его все еще можно найти в дальнейшей инверсии, как связь Олдема .

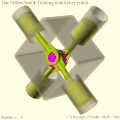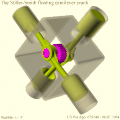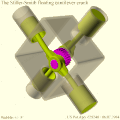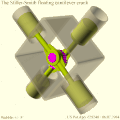
Механизм MultiFAZE . ^[5] В составном эксцентриковом механизме с несколькими фиксированными осями вала также используется эллиптическое движение, но здесь оно преобразуется во вращательное движение с помощью эксцентриковой зубчатой передачи вместо двухскоростного подшипника двойной нагрузки с размерными ограничениями, чтобы уменьшить трение и износ. Механизм MultiFAZE использовался в конфигурации с плавающей консолью в «действительно уникальном» двигателе Стиллера-Смита. ^[6]^[7] (см. Галерею ). Недостатки плавающей консольной системы являются предметом компьютерного моделирования с использованием стохастических методов и анализа методом конечных элементов. ^[8]^[9]

Галерея

Приблизительные прямые связи

Детали/звенья одного цвета имеют одинаковые размеры.

Связь Ватта
Рычаг параллельного движения Уоттса
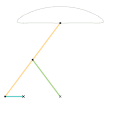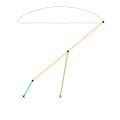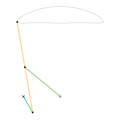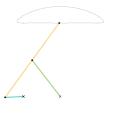
Связь Эванса "Кузнечик"
Связь Робертса
Чебышевская навеска
Чебышевская лямбда-связь
Связь с таблицей Чебышева
Связь Хеккена

Идеальные прямые связи

Детали/звенья одного цвета имеют одинаковые размеры.

Саррусовая связь (вариант Барса)
Саррусовая связь (вариант пластин)
Инвертор Поселье-Липкина
Инвертор Хартс 1
Хартс Инвестор 2 ^{[Примечание 1]}
Перролатц инвестор
Инверторный кайт Kempe 1 ^{[Примечание 1]}
Кайт-инвертор Kempe 2 ^{[Примечание 1]}
Кайт-инвертор Kempe 3 ^{[Примечание 1]}
Соединение Скотта Рассела (соединение ползуна) ^{[Примечание 1]}
Связь Скотта Рассела (связана со связью Поселье-Липкина)
Инвертор Брикара ^{[Примечание 1]}
Квадрупланарный инвертор Сильвестра-Кемпе 1 ^{[Примечание 1]}
Квадрупланарный инвертор Сильвестра-Кемпе 2 ^{[Примечание 1]}
Квадрупланарный инвертор Сильвестра-Кемпе 3
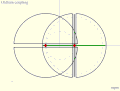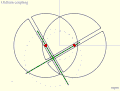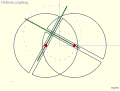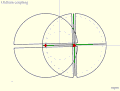
Инвестор Кумара-Камплинг ^{[Примечание 1]}

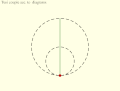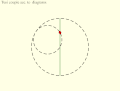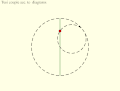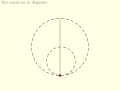
Пара Туси, эллиптическое движение: версии и инверсии

Пара Туси по схемам в переводе копии оригинального описания Туси: Малый круг катится внутри большого круга.
Пара Туси согласно переводу копии оригинального описания Туси: Круги вращаются в одном направлении, соотношение скоростей 1:2.
Взгляд Коперника на пару Туси: направление вращения и орбита движущегося круга равны и противоположны.
Инверсия №3
Инверсия №4
Инверсия №5 – передаточное число 1:3
Инверсия №6
Механизм Парсонса представляет собой удвоенную версию инверсии № 2 пары Туси, соединенной архимедовой трамвайной системой.
Муфта Олдема . Концы двух валов с прорезями (черного цвета) соединены крестовиной (зеленой). Сравните с парой Туси Инверсия №4.
Кинематика механизма MultiFAZE характеризуется параллелограммом ABCD. Большой пунктирный круг предназначен только для справки.

Сложные эксцентриковые механизмы с эллиптическим движением

Прямозубая шестерня с двумя зубьями катится внутри коронной шестерни с четырьмя зубьями: Архимед, Тузи или Кардано?
Гипоциклические шестерни Кардано: красные, зеленые и синие штифты совершают возвратно-поступательное движение в зависимости от диаметра кольцевой шестерни.
Три батута Архимеда на треугольном роторе, показывающие круговую орбиту средних точек батутов.
Двигатель X4 с углом поворота 60° и механизмом MultiFAZE с противовесами для полной балансировки.
Двигатель MultiFAZE 90° X4 с траверсами, трамбовочными механизмами и возвратно-поступательными балансирами/ползунами.
Принцип кривошипа Стиллера-Смита с плавающей консолью. Имитация колебаний и перерегулирований преувеличена для эффекта.
Плавающий консольно-шатунный двигатель Стиллера-Смита, вид сбоку

См. также

Примечания

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Рычаг имеет нестабильные положения, которые не учитываются. Для ясности меры по смягчению последствий указанных нестабильных положений не показаны.

Ссылки

^ Кемпе, Альфред Брей (1877). Как нарисовать прямую линию: лекция о связях . Макмиллан и компания. ISBN 978-1-4297-0244-7 .
^ Артоболевский Иван Иванович. Механизмы в современном машиностроении . ISBN 978-5-9710-5698-0 .
^ Четырехцилиндровый четырехтактный двигатель с двумя поршневыми компонентами, AJS Baker, ME Cross, Институт инженеров-механиков, Автомобильный отдел, Том 188 38/74
^ Эпициклический двигатель Парсонса
^ Патент № DE 3232974, опубликован в марте 1984 г.
^ Заявка на патент № US 628 248, поданная в июле 1984 г. (см. US 4 641 611).
↑ Профессора WVU разрабатывают «революционный» двигатель, Архив UPI, 5 ноября 1984 г.
^ Расчетные нагрузки системы плавающей передачи в механизме Стиллера-Смита
^ Двигатель Стиллера-Смита: анализ плавающей шестерни

Теория машин и механизмов, Джозеф Эдвард Шигли

Внешние ссылки

Корнельский университет (в архиве) - Модели прямолинейных механизмов
Альфред Кемпе (1877 г.). Как нарисовать прямую линию (PDF) . Макмиллан – через Калифорнийский университет в Ирвине .
Дайна Таймина . «Как нарисовать прямую линию — урок» . Корнеллский университет .
Моделирование с использованием программного обеспечения Molecular Workbench.
bham.ac.uk - А-кадр Харта (перетаскиваемая анимация), 6-тактная связь

[Note01-10] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Рычаг имеет нестабильные положения, которые не учитываются. Для ясности меры по смягчению последствий указанных нестабильных положений не показаны.

[1] Кемпе, Альфред Брей (1877). Как нарисовать прямую линию: лекция о связях . Макмиллан и компания. ISBN 978-1-4297-0244-7 .

[2] Артоболевский Иван Иванович. Механизмы в современном машиностроении . ISBN 978-5-9710-5698-0 .

[3] Четырехцилиндровый четырехтактный двигатель с двумя поршневыми компонентами, AJS Baker, ME Cross, Институт инженеров-механиков, Автомобильный отдел, Том 188 38/74

[4] Эпициклический двигатель Парсонса

[5] Патент № DE 3232974, опубликован в марте 1984 г.

[6] Заявка на патент № US 628 248, поданная в июле 1984 г. (см. US 4 641 611).

[7] Профессора WVU разрабатывают «революционный» двигатель, Архив UPI, 5 ноября 1984 г.

[8] Расчетные нагрузки системы плавающей передачи в механизме Стиллера-Смита

[9] Двигатель Стиллера-Смита: анализ плавающей шестерни

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[Примечание 1]