Механическое равновесие

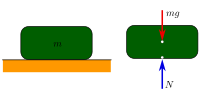
Объект, лежащий на поверхности, и соответствующая диаграмма свободного тела, показывающая силы, действующие на объект. Нормальная сила N равна, противоположна и коллинеарна гравитационной силе *mg,* поэтому результирующая сила и момент равны нулю. Следовательно, объект находится в состоянии статического механического равновесия.

В классической механике частица действующая на эту частицу , находится в механическом равновесии , если результирующая сила, равна нулю. ^[1]^: 39 В более широком смысле, физическая система, состоящая из многих частей, находится в механическом равновесии, если результирующая сила, действующая на каждую из ее отдельных частей, равна нулю. ^[1]^: 45–46^[2]

Помимо определения механического равновесия с точки зрения силы, существует множество альтернативных определений механического равновесия, которые все математически эквивалентны.

С точки зрения импульса система находится в равновесии, если импульс всех ее частей постоянен.
С точки зрения скорости система находится в равновесии, если скорость постоянна. * При вращательном механическом равновесии угловой момент объекта сохраняется, а чистый крутящий момент равен нулю. ^[2]

В более общем смысле, в консервативных системах равновесие устанавливается в точке конфигурационного пространства , где градиент потенциальной энергии по отношению к обобщенным координатам равен нулю.

Если частица, находящаяся в равновесии, имеет нулевую скорость, эта частица находится в статическом равновесии . ^[3]^[4] Поскольку все частицы, находящиеся в равновесии, имеют постоянную скорость, всегда можно найти инерциальную систему отсчета , в которой частица неподвижна относительно системы отсчета.

Стабильность [ править ]

Важным свойством систем, находящихся в механическом равновесии, является их устойчивость .

энергетическую стабильность потенциальную на Тест

В функции, описывающей потенциальную энергию системы, равновесие системы можно определить с помощью исчисления . Система находится в механическом равновесии в критических точках функции, описывающей потенциальную энергию системы. Эти точки можно найти, используя тот факт, что производная функции равна нулю в этих точках. Чтобы определить, является ли система стабильной или нестабильной, тест второй производной применяется . С $V$ Обозначая статическое уравнение движения системы с одной степенью свободы, можно провести следующие вычисления:

Вторая производная < 0: Потенциальная энергия находится в локальном максимуме, что означает, что система находится в неустойчивом равновесном состоянии. Если систему сместить на сколь угодно малое расстояние от состояния равновесия, силы системы заставят ее отойти еще дальше.

Вторая производная > 0: Потенциальная энергия находится на уровне локального минимума. Это устойчивое равновесие. Реакцией на небольшое возмущение являются силы, стремящиеся восстановить равновесие. Если для системы возможно более одного устойчивого состояния равновесия, любое равновесие, потенциальная энергия которого выше абсолютного минимума, представляет собой метастабильные состояния.

Вторая производная = 0: Состояние нейтрально до самого низкого порядка и почти остается в равновесии при небольшом перемещении. Чтобы исследовать точную устойчивость системы, производные более высокого порядка можно изучить . Состояние нестабильно, если наименьшая ненулевая производная имеет нечетный порядок или имеет отрицательное значение, и стабильно, если наименьшая ненулевая производная имеет четный порядок и имеет положительное значение. Если все производные равны нулю, то невозможно сделать какие-либо выводы только по производным. Например, функция $e^{-1/x^{2}}$ (определяется как 0 при x=0) имеет все производные, равные нулю. В то же время эта функция имеет локальный минимум при x=0, поэтому является устойчивым равновесием. Если эту функцию умножить на функцию Sign , все производные по-прежнему будут равны нулю, но это станет нестабильным равновесием.

Схема шара, находящегося в нейтральном равновесии.

Функция локально постоянна: В истинно нейтральном состоянии энергия не меняется, и состояние равновесия имеет конечную ширину. Иногда это называют состоянием минимальной стабильности, состоянием безразличия или нестабильным равновесием.

При рассмотрении более чем одного измерения можно получить разные результаты в разных направлениях, например стабильность относительно смещений в направлении x , но нестабильность в направлении y , случай, известный как седловая точка . Обычно равновесие называют устойчивым только в том случае, если оно стабильно во всех направлениях.

Статически неопределимая система [ править ]

Иногда недостаточно информации о силах, действующих на тело, чтобы определить, находится оно в равновесии или нет. Это делает ее статически неопределимой системой.

Примеры [ править ]

Стационарный объект (или набор объектов) находится в «статическом равновесии», которое является частным случаем механического равновесия. Пресс-папье на столе — пример статического равновесия. Другие примеры включают скульптуру баланса на камне или стопку блоков в игре Дженга , при условии, что скульптура или стопка блоков не находятся в состоянии разрушения .

Движущиеся объекты также могут находиться в равновесии. Ребенок, скатывающийся с горки с постоянной скоростью, находился бы в механическом равновесии, но не в статическом равновесии (в системе отсчета земли или горки).

Другим примером механического равновесия является человек, прижимающий пружину к определенной точке. Он или она может подтолкнуть его в произвольную точку и удерживать там, при этом сжимающая нагрузка и реакция пружины становятся равными. В этом состоянии система находится в механическом равновесии. Когда сжимающая сила снимается, пружина возвращается в исходное состояние.

Особый интерес представляет минимальное число статических равновесий однородных выпуклых тел (при покое под действием силы тяжести на горизонтальной поверхности). В плоском случае минимальное количество — 4, тогда как в трехмерном можно построить объект всего с одной устойчивой и одной неустойчивой точкой равновесия. ^[5] Такой объект называется гёмбёк .

См. также [ править ]

Примечания и ссылки [ править ]

^ Jump up to: Перейти обратно: ^а ^б Джон Л. Синдж и Байрон А. Гриффит (1949). Основы механики (2-е изд.). МакГроу-Хилл.
^ Jump up to: Перейти обратно: ^а ^б Бир Ф.П., Джонстон Э.Р., Мазурек Д.Ф., Корнелл П.Дж. и Айзенберг, Э.Р. (2009). Векторная механика для инженеров: статика и динамика (9-е изд.). МакГроу-Хилл. п. 158. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Герберт Чарльз Корбен и Филип Стел (1994). Классическая механика (переиздание 1960 г., второе изд.). Публикации Курьера Дувра. п. 113. ИСБН 0-486-68063-0 .
^ Лакшмана К. Рао; Дж. Лакшминарасимхан; Раджу Сетураман; Шринивасан М. Сивакумар (2004). Инженерная механика . PHI Learning Pvt. ООО п. 6. ISBN 81-203-2189-8 .
^ «Математика» . Гёмбёк . 2021 . Проверено 12 ноября 2023 г.

Дальнейшее чтение [ править ]

Мэрион Дж.Б. и Торнтон С.Т. (1995) Классическая динамика частиц и систем. Четвертое издание, Harcourt Brace & Company.

[Synge-1] Jump up to: Перейти обратно: ^а ^б Джон Л. Синдж и Байрон А. Гриффит (1949). Основы механики (2-е изд.). МакГроу-Хилл.

[beer-2] Jump up to: Перейти обратно: ^а ^б Бир Ф.П., Джонстон Э.Р., Мазурек Д.Ф., Корнелл П.Дж. и Айзенберг, Э.Р. (2009). Векторная механика для инженеров: статика и динамика (9-е изд.). МакГроу-Хилл. п. 158. {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[Stehle-3] Герберт Чарльз Корбен и Филип Стел (1994). Классическая механика (переиздание 1960 г., второе изд.). Публикации Курьера Дувра. п. 113. ИСБН 0-486-68063-0 .

[Rao-4] Лакшмана К. Рао; Дж. Лакшминарасимхан; Раджу Сетураман; Шринивасан М. Сивакумар (2004). Инженерная механика . PHI Learning Pvt. ООО п. 6. ISBN 81-203-2189-8 .

[5] «Математика» . Гёмбёк . 2021 . Проверено 12 ноября 2023 г.

[1]

[2]

[3]

[4]

[5]