Дробь единицы

Чтобы узнать о долях единицы измерения, см. Префикс единицы измерения .

Кусочки примерно 1/8 пиццы.

Единичная дробь — это положительная дробь с единицей в числителе , 1/ n . Это мультипликативный обратный (обратный) знаменатель дроби , который должен быть положительным натуральным числом . Примеры: 1/1, 1/2, 1/3, 1/4, 1/5 и т. д. Когда объект делится на равные части, каждая часть представляет собой единичную долю целого.

Умножение двух единичных дробей дает еще одну единичную дробь, но другие арифметические операции не сохраняют единичные дроби. В модульной арифметике дробные единицы можно преобразовать в эквивалентные целые числа, что позволяет преобразовать модульное деление в умножение. Каждое рациональное число можно представить как сумму различных долей единицы; эти представления называются египетскими дробями на основании их использования в древнеегипетской математике . Многие бесконечные суммы единичных дробей имеют математический смысл.

В геометрии единичные дроби можно использовать для характеристики кривизны групп треугольников и касаний окружностей Форда . Единичные дроби обычно используются при справедливом делении , и это знакомое применение используется в математическом образовании как ранний шаг к пониманию других дробей. Единичные дроби широко распространены в теории вероятностей из-за принципа безразличия . Они также имеют применение в комбинаторной оптимизации и при анализе структуры частот в спектральном ряду водорода .

Арифметика

Единичные дроби – это рациональные числа , которые можно записать в виде $${\frac {1}{n}},$$ где $n$ может быть любым положительным натуральным числом . Таким образом, они являются мультипликативными обратными числами положительных целых чисел. Когда что-то разделено на $n$ равные части, каждая часть представляет собой $1/n$ часть целого.

Элементарная арифметика

Умножение любых двух единичных дробей приводит к получению продукта, который представляет собой другую единичную дробь: $${\frac {1}{x}}\times {\frac {1}{y}}={\frac {1}{xy}}.$$Однако, добавив , вычитание , или деление двух единичных дробей дает результат, который обычно не является единичной дробью: $${\frac {1}{x}}+{\frac {1}{y}}={\frac {x+y}{xy}}$$

$${\frac {1}{x}}-{\frac {1}{y}}={\frac {y-x}{xy}}$$

$${\frac {1}{x}}\div {\frac {1}{y}}={\frac {y}{x}}.$$

Как показывает последняя из этих формул, каждую дробь можно выразить как частное двух единичных дробей.

Модульная арифметика

В модульной арифметике любую единичную дробь можно преобразовать в эквивалентное целое число с помощью расширенного алгоритма Евклида . Это преобразование можно использовать для модульного деления: деления на число. $x$, модуль $y$, может быть выполнено путем преобразования единичной дроби $1/x$ в эквивалентное целое число по модулю $y$, а затем умножить на это число.

Более подробно предположим, что $x$ является относительно простым для $y$ (иначе деление на $x$ не определяется по модулю $y$). Расширенный алгоритм Евклида для определения наибольшего общего делителя можно использовать для поиска целых чисел. $a$ и $b$ так, что тождество Безу удовлетворено: $$\displaystyle ax+by=\gcd(x,y)=1.$$По форме- $y$ арифметика, термин $by$ можно исключить, так как оно равно нулю по модулю $y$. Это оставляет $$\displaystyle ax\equiv 1{\pmod {y}}.$$То есть, $a$ является модульной обратной величиной $x$, число, которое при умножении на $x$ производит один. Эквивалентно, $$a\equiv {\frac {1}{x}}{\pmod {y}}.$$Таким образом, деление на $x$ (модуль $y$) вместо этого можно выполнить путем умножения на целое число $a$.

Комбинации

Некоторые конструкции в математике включают объединение нескольких дробных единиц вместе, часто путем их сложения.

Конечные суммы

Смотрите также: Список сумм обратных величин § Конечное число членов

Любое положительное рациональное число можно записать как сумму различных дробных единиц несколькими способами. Например,

${\frac {4}{5}}={\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{20}}={\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{10}}.$

Эти суммы называются египетскими дробями , поскольку древние египетские цивилизации использовали их в качестве обозначения более общих рациональных чисел . Сегодня по-прежнему существует интерес к анализу методов, используемых древними для выбора среди возможных представлений дробного числа и вычислений с использованием таких представлений. Тема египетских дробей также вызвала интерес в современной теории чисел ; например, гипотеза Эрдеша – Грэма и гипотеза Эрдеша – Штрауса касаются сумм единичных долей, как и определение гармонических чисел Оре .

Узор из сферических треугольников с симметрией отражения по каждому краю треугольника. Сферические модели отражения, подобные этому, с $2x$, $2y$, и $2z$ треугольники в каждой вершине (здесь $x,y,z=2,3,5$) существуют только тогда, когда ${\tfrac {1}{x}}+{\tfrac {1}{y}}+{\tfrac {1}{z}}>1$.

В геометрической теории групп группы треугольников подразделяются на евклидовы, сферические и гиперболические случаи в зависимости от того, равна ли связанная сумма единичных дробей единице, больше единицы или меньше единицы соответственно.

Бесконечная серия

Смотрите также: Список сумм обратных величин § Бесконечно много членов

Члены многих известных бесконечных рядов представляют собой доли единицы. К ним относятся:

• Гармонический ряд — сумма всех положительных единичных дробей. Эта сумма расходится, а ее частичные суммы $${\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}$$ близко приближается к натуральному логарифму $n$ плюс постоянная Эйлера-Машерони . Изменение каждого последующего сложения на вычитание дает чередующийся гармонический ряд, сумма которого равна натуральному логарифму 2 : $$\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$$
• Формула Лейбница для π : $$1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots ={\frac {\pi }{4}}.$$
• Базельская проблема касается суммы долей квадратных единиц: $$1+{\frac {1}{4}}+{\frac {1}{9}}+{\frac {1}{16}}+\cdots ={\frac {\pi ^{2}}{6}}.$$ Точно так же константа Апери — это иррациональное число , сумма кубических долей единицы.
• Бинарная геометрическая прогрессия – это $$1+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =2.$$

Матрицы

Матрица Гильберта – это квадратная матрица, в которой элементы $i$все антидиагонали равны единичной дроби $1/i$. То есть в нем есть элементы $$B_{i,j}={\frac {1}{i+j-1}}.$$Например, матрица $${\begin{bmatrix}1&{\frac {1}{2}}&{\frac {1}{3}}\\{\frac {1}{2}}&{\frac {1}{3}}&{\frac {1}{4}}\\{\frac {1}{3}}&{\frac {1}{4}}&{\frac {1}{5}}\end{bmatrix}}$$является матрицей Гильберта. Он обладает необычным свойством: все элементы его обратной матрицы являются целыми числами. Точно так же Ричардсон (2001) определил матрицу, элементами которой являются единичные дроби, знаменателями которых являются числа Фибоначчи : $$C_{i,j}={\frac {1}{F_{i+j-1}}},$$где $F_{i}$ обозначает $i$число Фибоначчи. Он называет эту матрицу матрицей Филберта, и она обладает тем же свойством: иметь целочисленную обратную матрицу.

Смежность и круги Форда

Дроби с касательными кругами Форда отличаются на единицу дроби

Две фракции $a/b$ и $c/d$ (в самых простых терминах) называются смежными, если $$ad-bc=\pm 1,$$ откуда следует, что они отличаются друг от друга на долю единицы: $$\left|{\frac {1}{a}}-{\frac {1}{b}}\right|={\frac {|ad-bc|}{bd}}={\frac {1}{bd}}.$$Например, ${\tfrac {1}{2}}$ и ${\tfrac {3}{5}}$ находятся рядом: $1\cdot 5-2\cdot 3=-1$ и ${\tfrac {3}{5}}-{\tfrac {1}{2}}={\tfrac {1}{10}}$. Однако некоторые пары дробей, разность которых равна единице дроби, не являются соседними в этом смысле: например, ${\tfrac {1}{3}}$ и ${\tfrac {2}{3}}$ различаются на долю единицы, но не являются соседними, поскольку для них $ad-bc=3$.

Эта терминология возникла в результате изучения кругов Форда . Это система кругов, которые касаются числовой прямой в данной дроби и имеют диаметр в квадрате знаменателя дроби. Фракции $a/b$ и $c/d$ смежны тогда и только тогда, когда их окружности Форда являются касательными .

Приложения

Справедливое разделение и математическое образование

В математическом образовании единичные дроби часто вводятся раньше, чем другие виды дробей, из-за простоты визуального объяснения их как равных частей целого. Обычное практическое использование дробей единиц состоит в том, чтобы разделить еду поровну между несколькими людьми, а упражнения по выполнению такого рода справедливого деления являются стандартным примером в классе для обучения студентов работе с дробями единиц.

Вероятность и статистика

Шестигранный кубик имеет вероятность выпадения 1/6 на каждой стороне.

При равномерном распределении в дискретном пространстве все вероятности равны долям единицы. Из-за принципа безразличия вероятности этой формы часто возникают в статистических расчетах.

возникают неравные вероятности, связанные с долями единицы В законе Ципфа . Это означает, что для многих наблюдаемых явлений, связанных с выбором элементов из упорядоченной последовательности, вероятность того, что $n$выбранный элемент пропорционален доле единицы $1/n$.

Комбинаторная оптимизация

При изучении комбинаторной оптимизации задач задачи упаковки корзин включают в себя входную последовательность предметов дробных размеров, которые необходимо поместить в корзины, емкость которых (общий размер предметов, помещенных в каждую корзину) равна единице. Исследование этих проблем включало изучение задач ограниченной упаковки в контейнеры, где размеры предметов представляют собой доли единицы.

Одной из причин этого является тестовый пример для более общих методов упаковки в контейнеры. Другой вариант включает в себя форму планирования «вертушки» , при которой набор сообщений одинаковой длины должен многократно транслироваться по ограниченному числу каналов связи, при этом каждое сообщение имеет максимальную задержку между моментами начала его повторных трансляций. Товар, задержка которого составляет $k$ раз длина сообщения должна занимать долю по крайней мере $1/k$ временных интервалов на канале, которому он назначен, поэтому решение проблемы планирования может быть получено только путем решения проблемы упаковки ячеек единичных фракций с каналами в качестве ячеек и фракций. $1/k$ как размеры товара.

Даже в случае проблем с упаковкой в ​​корзину с предметами произвольных размеров может быть полезно округлить размер каждого предмета до следующей большей доли единицы, а затем применить алгоритм упаковки в корзину, специально предназначенный для размеров единичных фракций. В частности, метод упаковки гармонических ячеек делает именно это, а затем упаковывает каждую корзину, используя предметы только с одним округленным размером дроби.

Физика

Спектральный ряд водорода в логарифмическом масштабе. Частоты эмиссионных линий пропорциональны разностям пар долей единицы.

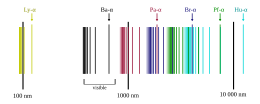
Энергетические уровни фотонов , которые могут быть поглощены или испущены атомом водорода, согласно формуле Ридберга , пропорциональны разностям двух единичных долей. Объяснение этому явлению дает модель Бора , согласно которой энергетические уровни электронных орбиталей в атоме водорода обратно пропорциональны квадратным долям единицы, а энергия фотона квантуется разнице между двумя уровнями.

Артур Эддингтон утверждал, что константа тонкой структуры представляет собой долю единицы. Сначала он думал, что это 1/136, но позже изменил свою теорию на 1/137. Это утверждение было опровергнуто, учитывая, что текущие оценки постоянной тонкой структуры составляют (с точностью до 6 значащих цифр) 1/137,036.

См. также

• Загадка о наследстве из 17 животных - головоломка, включающая справедливое разделение на отдельные дроби.
• Submultiple — число, которое дает единичную дробь при использовании в качестве числителя с заданным знаменателем.
• Суперчастичное отношение , единица плюс единичная дробь, важное для музыкальной гармонии.