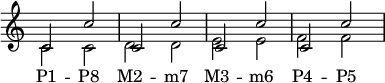Интервал (музыка)

$\макет { ширина линии = 60\мм отступ = 0\мм } \относительный с''{ \clef treble \time 3/1 \hide Staff.TimeSignature d,1 гс \бар "||" \перерыв \time 1/1 <d f> \bar "||" <d g> \bar "||" <f g> \bar "||" }$

Мелодические и гармонические интервалы

В теории музыки интервал – это разница в высоте двух звуков. ^[1] Интервал может быть описан как горизонтальный , линейный или мелодический, если он относится к последовательно звучащим тонам, например, к двум соседним тонам в мелодии, и как вертикальный или гармонический , если он относится к одновременно звучащим тонам, например, в аккорде . ^[2]^[3]

В западной музыке интервалы чаще всего представляют собой различия между нотами диатонической гаммы . Интервалы между последовательными нотами гаммы также известны как шаги гаммы. Наименьший из этих интервалов — полутон . Интервалы меньше полутона называются микротонами . Они могут быть образованы с использованием нот различных видов недиатонических гамм. Некоторые из самых маленьких из них называются запятыми и описывают небольшие расхождения, наблюдаемые в некоторых системах настройки , между энгармонически эквивалентными нотами, такими как C ♯ и D ♭ . Интервалы могут быть сколь угодно малыми и даже незаметными для человеческого уха.

С физической точки зрения интервал — это соотношение двух звуковых частот. Например, любые две ноты, находящиеся на расстоянии октавы, имеют соотношение частот 2:1. Это означает, что последовательное увеличение высоты звука на один и тот же интервал приводит к экспоненциальному увеличению частоты, хотя человеческое ухо воспринимает это как линейное увеличение высоты звука. По этой причине интервалы часто измеряются в центах — единице, полученной из логарифма отношения частот.

В западной теории музыки наиболее распространенная схема наименования интервалов описывает два свойства интервала: качество ( совершенный, мажорный, минорный, увеличенный, уменьшенный) и число (унисон, секунда, треть и т. д.). Примеры включают второстепенную треть или идеальную квинту . интервал Эти названия определяют не только разницу в полутонах между верхними и нижними нотами, но и то, как пишется . Важность правописания проистекает из исторической практики дифференциации частотных соотношений энгармонических интервалов, таких как G – G ♯ и G – A ♭ . ^[4]

Размер [ править ]

$\относительный с''{ \hide Staff.TimeSignature <cc,>1 | в,4 в'с,2 }$

Пример: Идеальная октава ноты C в равной темперации и точной интонации: 2/1 = 1200 центов.

Размер интервала (также известный как его ширина или высота) может быть представлен с использованием двух альтернативных и одинаково допустимых методов, каждый из которых подходит для своего контекста: отношений частот или центов.

Отношения частот [ править ]

Размер интервала между двумя нотами можно измерить соотношением их частот . Когда музыкальный инструмент настроен с использованием системы точной интонационной настройки, размер основных интервалов может быть выражен маленькими целыми числами, такими как 1:1 ( унисон ), 2:1 ( октава ), 5:3 ( большая секста). ), 3:2 ( идеальная пятая ), 4:3 ( идеальная четвёртая ), 5:4 ( большая треть ), 6:5 ( второстепенная треть ). Интервалы с малоцелыми отношениями часто называют просто интервалами , или чистыми интервалами .

Однако чаще всего в настоящее время музыкальные инструменты настраиваются с использованием другой системы настройки, называемой 12-тональной равнотемперированной . Как следствие, размеры большинства равнотемперированных интервалов не могут быть выражены малыми целыми числами, хотя они очень близки к размерам соответствующих справедливых интервалов. Например, равнотемперированная квинта имеет соотношение частот 2. ^{7 ⁄ 12}:1, примерно равно 1,498:1 или 2,997:2 (очень близко к 3:2). Для сравнения размера интервалов в разных системах настройки см. § Размер интервалов, используемых в разных системах настройки .

Центы [ править ]

Стандартная система сравнения размеров интервалов — в центах . Цент — логарифмическая единица измерения. Если частота выражается в логарифмической шкале , и по этой шкале расстояние между данной частотой и ее дублем (также называемым октавой ) делится на 1200 равных частей, каждая из этих частей равна одному центу. В двенадцатитоновой равнотемперированной (12-ТЕТ) системе настройки, в которой все полутона имеют одинаковый размер, размер одного полутона составляет ровно 100 центов. Следовательно, в 12-TET цент также можно определить как одну сотую полутона .

Математически размер интервала от частоты f ₁ до частоты f ₂ в центах равен

n=1200\cdot \log _{2}\left({\frac {f_{2}}{f_{1}}}\right)

Основные интервалы [ править ]

В таблице приведены наиболее употребительные условные названия интервалов между нотами хроматической гаммы . Идеальный унисон (также известный как идеальное простое число) ^[5]интервал, образованный двумя одинаковыми нотами. Его размер составляет ноль центов . Полутон — это интервал , — это любой интервал между двумя соседними нотами хроматической гаммы, целый тон охватывающий два полутона (например, большая секунда ), а тритон — это интервал, охватывающий три тона или шесть полутонов (например, дополненная четвёртая). ^[а] В редких случаях термин дитон также используется для обозначения интервала, охватывающего два целых тона (например, мажорную треть ), или, более строго, как синоним мажорной терции.

Интервалы с разными названиями могут охватывать одинаковое количество полутонов и даже иметь одинаковую ширину. Например, интервал от D до F ♯ — это большая терция , а от D до G ♭ — уменьшенная кварта . Однако оба они охватывают 4 полутона. Если инструмент настроен так, что 12 нот хроматической гаммы расположены на одинаковом расстоянии друг от друга (как в равнотемперированной ), эти интервалы также имеют одинаковую ширину. А именно, все полутона имеют ширину 100 центов , а все интервалы, охватывающие 4 полутона, имеют ширину 400 центов.

Перечисленные здесь имена невозможно определить только путем подсчета полутонов. Правила их определения описаны ниже. Другие имена, определенные с использованием других соглашений об именах, перечислены в отдельном разделе . интервалы меньше одного полутона (запятые или микротоны) и больше одной октавы Ниже представлены (сложные интервалы).

Количество полутона	Минор, мажор, или идеальные интервалы	Короткий	Дополненная или уменьшенные интервалы	Короткий	Широко используемый альтернативные имена	Короткий	Аудио
0	Идеальный унисон	П1	Уменьшенная секунда	d2			Играть ^ⓘ
1	Незначительная секунда	м2	Расширенный унисон	А1	Полутон , полутон, полутон	С	Играть ^ⓘ
2	Главный второй	М2	Уменьшенная треть	д3	Тон , целый тон, целый шаг	Т	Играть ^ⓘ
3	Малая треть	m3	Дополненная секунда	А2			Играть ^ⓘ
4	Основная треть	M3	Уменьшенный четвертый	d4			Играть ^ⓘ
5	Идеальная четвертая	П4	Дополненная треть	А3			Играть ^ⓘ
6			Уменьшенная пятая часть	d5	Тритон	ТТ	Играть ^ⓘ
6			Дополненная четвертая	A4	Тритон	ТТ	Играть ^ⓘ
7	Идеальная пятая часть	П5	Уменьшенная шестая позиция	d6			Играть ^ⓘ
8	Малая шестая	м6	Дополненная пятая	А5			Играть ^ⓘ
9	Майор шестой	М6	Уменьшенный седьмой	d7			Играть ^ⓘ
10	Минорная седьмая	м7	Дополненная шестая	А6			Играть ^ⓘ
11	Майор седьмой	М7	Уменьшенная октава	d8			Играть ^ⓘ
12	Идеальная октава	Р8	Дополненная седьмая	A7			Играть ^ⓘ

Количество и качество интервалов [ править ]

В западной теории музыки интервал называется по его номеру (также называемому диатоническим числом, размером интервала). ^[6] или общий интервал ^[7]) и качество . Например, мажорная терция (или M3 ) — это имя интервала, в котором термин мажор ( M ) описывает качество интервала, а терция ( 3 ) указывает его номер.

Номер [ править ]

Номер интервала — это количество названий букв или позиций нотного стана (строк и пробелов), которые он охватывает, включая позиции обеих нот, образующих интервал. Например, интервал C–G является квинтой (обозначается P5 ), поскольку ноты от C до G над ним охватывают имена из пяти букв (C, D, E, F, G) и занимают пять последовательных нотных должностей, включая позиции C и G. В таблице и на рисунке выше показаны интервалы с номерами от 1 (например, P1 ) до 8 (например, P8 ). Интервалы с большими номерами называются составными интервалами .

существует однозначное соответствие . диатонической гаммы Между позициями нотного аппарата и ступенями (нотами диатонической гаммы ) ^[б]Это означает, что номера интервалов также можно определить путем подсчета ступеней диатонической гаммы, а не позиций нотного стана, при условии, что две ноты, образующие интервал, взяты из диатонической гаммы. А именно, C–G является квинтой, потому что в любой диатонической гамме, содержащей C и G, последовательность от C до G включает пять нот. Например, в диатонической гамме A мажор ♭ пять нот: C–D ♭ –E ♭ –F–G (см. рисунок). Это справедливо не для всех видов весов. Например, в хроматической гамме восемь нот от C до G: (C–C ♯ –D–D ♯ –E–F–F ♯ –G). По этой причине интервальные числа также называются диатоническими числами , и это соглашение называется диатонической нумерацией .

добавить какие-либо случайные звуки Если к нотам, образующим интервал, , ноты по определению не изменят своего нотного положения. Как следствие, любой интервал имеет тот же номер интервала, что и соответствующий ему натуральный интервал, образованный теми же нотами без случайностей. Например, интервалы C – G ♯ (охватывающие 8 полутонов) и C ♯ –G (охватывающие 6 полутонов) являются квинтами, как и соответствующий натуральный интервал C – G (7 полутонов).

Обратите внимание, что номера интервалов представляют собой общее количество включенных должностей персонала или названий заметок, а не разницу между конечными точками. Другими словами, нижний тон начинают считать за единицу, а не за ноль. По этой причине интервал C – C, идеальный унисон, называется простым числом (что означает «1»), даже если между конечными точками нет разницы. Продолжая, интервал C–D — это секунда, но D — это только одна позиция нотоносца или ступень диатонической гаммы выше C. Точно так же C–E является терцией, но E — всего на две позиции нотоносца выше C, и так далее. . Как следствие, соединение двух интервалов всегда дает интервал номер на единицу меньше их суммы. Например, интервалы C–E и E–G являются терциями, но вместе они образуют квинту (C–G), а не шестую. Точно так же стопка из трех третей, например C–E, E–G и G–B, представляет собой седьмую (C–B), а не девятую.

Эта схема применима к интервалам до октавы (12 полутонов). Чтобы узнать о больших интервалах, см. § Сложные интервалы ниже.

Качество [ править ]

Интервалы, образованные нотами диатонической гаммы до мажор.

Название любого интервала дополнительно уточняется с использованием терминов совершенный ( P ), основной ( M ), минорный ( m ), увеличенный ( A ) и уменьшенный ( d ). Это называется его интервальным качеством (или модификатором ^[8]^[7]). Возможны вдвое уменьшенные и вдвое увеличенные интервалы, но это довольно редко, поскольку встречается только в хроматических контекстах. Сочетание числа (или родового интервала) и качества (или модификатора) называется конкретным интервалом . ^[7] диатонический интервал (иногда используется только для интервалов, встречающихся в диатонической гамме), или просто интервал . ^[8]

Качество составного интервала — это качество простого интервала, на котором он основан. Некоторые другие квалификаторы, такие как нейтральный , субминорный и супермажорный, используются для недиатонических интервалов .

Идеально [ править ]

Идеальные интервалы на C: PU , П4 , П5 , P8

Совершенные интервалы называются так потому, что традиционно считались совершенно созвучными. ^[9] хотя в западной классической музыке идеальная кварта иногда рассматривалась как не совсем идеальное созвучие, когда ее функция была контрапунктной . ^{[ нечеткий ]} И наоборот, минорные, мажорные, увеличенные или уменьшенные интервалы обычно считаются менее согласными и традиционно классифицируются как посредственные созвучия, несовершенные созвучия или почти диссонансы. ^[9]

В диатонической гамме ^[б]все унисоны ( P1 ) и октавы ( P8 ) идеальны. Большинство четвертых и пятых тона также идеальны ( P4 и P5 ) с пятью и семью полутонами соответственно. Одно появление кварты увеличивается ( A4 ), а одна квинта уменьшается ( d5 ), оба охватывают шесть полутонов. Например, в гамме до мажор A4 находится между F и B, а d5 — между B и F (см. таблицу).

По определению, обращение идеального интервала также является совершенным. Поскольку инверсия не меняет высоту звука двух нот, она практически не влияет на уровень их созвучия (совпадения их гармоник ). И наоборот, другие виды интервалов имеют противоположное качество по отношению к их инверсии. Инверсия большого интервала — это малый интервал, инверсия увеличенного интервала — уменьшенный интервал.

Мажор и минор [ править ]

Мажорные и минорные интервалы на C: m2 , М2 , m3 , M3 , м6 , М6 , м7 , М7

Как показано в таблице, диатоническая гамма ^[б]определяет семь интервалов для каждого номера интервала, каждый из которых начинается с отдельной ноты (семь унисонов, семь секунд и т. д.). Интервалы, образованные нотами диатонической гаммы, называются диатоническими. За исключением унисонов и октав, диатонические интервалы с заданным номером интервала всегда встречаются в двух размерах, различающихся на один полутон. Например, шесть квинт охватывают семь полутонов. Другой охватывает шесть полутонов. Четыре из третей охватывают три полутона, остальные — четыре. Если один из двух вариантов представляет собой идеальный интервал, другой называется либо уменьшенным (т.е. суженным на один полутон), либо увеличенным (т.е. расширенным на один полутон). В противном случае большая версия называется мажорной, а меньшая — минорной. Например, поскольку квинта из 7 полутонов представляет собой идеальный интервал ( P5 ), квинта из 6 полутонов называется «уменьшенной квинтой» ( d5 ). И наоборот, поскольку ни один из видов терций не является совершенным, больший называется «большой терцией» ( M3 ), меньший — «малой терцией» ( m3 ).

В диатонической гамме ^[б] унисоны и октавы всегда квалифицируются как совершенные, кварты - как совершенные или увеличенные, квинты - как совершенные или уменьшенные, а все остальные интервалы (секунды, терции, шестые, септимы) - как мажорные или минорные.

Увеличение и уменьшение [ править ]

Увеличенные и уменьшенные интервалы на C: d2 , А2 , д3 , А3 , d4 , A4 , d5 , А5 , d6 , А6 , d7 , A7 , d8 , А8

Увеличенные интервалы шире на один полутон, чем совершенные или мажорные интервалы, при том же количестве интервалов (т. е. охватывая то же количество штатных должностей): они шире на хроматический полутон . С другой стороны, уменьшенные интервалы уже на один полутон, чем идеальные или минорные интервалы с тем же номером интервала: они уже на хроматический полутон. Например, увеличенная треть, такая как C – E ♯, охватывает пять полутонов, превышая большую треть (C – E) на один полутон, а уменьшенная треть, такая как C ♯ –E ♭, охватывает два полутона, не дотягивая до второстепенной трети. (C – E ♭ ) на один полутон.

Увеличенная кварта ( A4 ) и уменьшенная квинта ( d5 ) — единственные увеличенные и уменьшенные интервалы, которые появляются в диатонических гаммах. ^[б] (см. таблицу).

Пример [ править ]

Ни количество, ни качество интервала нельзя определить только путем подсчета полутонов . Как объяснялось выше, необходимо также учитывать количество штатных должностей.

Например, как показано в таблице ниже, существует четыре полутона между A ♭ и B ♯ , между A и C ♯ , между A и D ♭ и между A ♯ и E. , но

A ♭ –B ♯ является секундой, поскольку включает в себя две нотные позиции (A, B), и она увеличивается вдвое, поскольку превышает большую секунду (например, A–B) на два полутона.
A – C ♯ является терцией, поскольку охватывает три нотных позиции (A, B, C), и является мажорной, поскольку охватывает 4 полутона.
A – D ♭ - это кварта, поскольку она охватывает четыре нотных позиции (A, B, C, D), и она уменьшается, поскольку не достигает идеальной кварты (например, A – D) на один полутон.
А ♯ - Е является квинтой, поскольку включает в себя пять нотных позиций (A, B, C, D, E), и она уменьшается в три раза, поскольку отстает от идеальной квинты (например, A–E) на три полутона.

Число полутонов	Название интервала	Штатные должности
Число полутонов	Название интервала	1	2	3	4	5
4	дважды увеличенная секунда ( АА2 )	A ♭	B ♯
4	мажорная треть ( M3 )	А		C ♯
4	уменьшенная четвертая ( d4 )	А			D ♭
4	тройно уменьшенная пятая часть ( ddd5 )	A ♯				И

Сокращенное обозначение [ править ]

Интервалы часто обозначаются буквами P — идеальный, m — минор , M — мажор , d — уменьшенный , A — увеличенный , за которым следует номер интервала. Обозначения М и Р часто опускаются. Октава — P8 , а унисон обычно называют просто «унисон», но может обозначаться как P1. Тритон собой , увеличенная кварта или уменьшенная квинта, часто представляет ТТ . Интервальные качества также могут быть сокращены до perf , min , maj , dim , aug . Примеры:

м2 (или мин2): меньшая секунда,
M3 (или maj3): мажорная терция,
A4 (или aug4): дополненная четвертая,
d5 (или dim5): уменьшенная пятая часть,
P5 (или perf5): идеальная пятая часть.

Инверсия [ править ]

Простой интервал (т. е. интервал, меньший или равный октаве) можно инвертировать , повышая нижний тон на октаву или понижая верхний тон на октаву. Например, кварта от нижнего «до» к более высокому «фа» может быть перевернута, чтобы получить квинту от более низкого «фа» к более высокому «до».

${ \override Score.TimeSignature #'stencil = ##f \override Score.SpacingSpanner.strict-note-spacing = ##t \set Score.proportionalNotationDuration = #(ly:make-moment 1/4) \новый персонал << \ключ скрипичный \время 4/4 \новый голос \relative c' { \stemUp c2 c' c, c' c, c' c, c' } \новый голос \relative c' { \stemDown c2 cddeeff } \addlyrics { "P1" -- "P8" "M2" -- "m7" "M3" -- "m6" "P4" -- "P5" } >> }$

Существует два правила определения количества и качества обращения любого простого интервала: ^[10]

Номер интервала и номер его обращения всегда в сумме дают девять (4 + 5 = 9, в только что приведенном примере).
Инверсия большого интервала становится второстепенным интервалом, и наоборот; обращение идеального интервала также совершенно; инверсия увеличенного интервала есть уменьшенный интервал, и наоборот; инверсия дважды увеличенного интервала является дважды уменьшенным интервалом, и наоборот.

Например, интервал от C до E ♭ над ним представляет собой второстепенную терцию. Согласно двум только что данным правилам, интервал от E ♭ до ноты C над ним должен составлять большую шестую часть.

Поскольку составные интервалы больше октавы, «инверсия любого составного интервала всегда такая же, как и инверсия простого интервала, из которого он составлен». ^[11]

Для интервалов, определяемых их соотношением, инверсия определяется путем изменения отношения и умножения отношения на 2, пока оно не станет больше 1. Например, инверсия соотношения 5:4 представляет собой соотношение 8:5.

Для интервалов, определяемых целым числом полутонов, инверсия получается вычитанием этого числа из 12.

Поскольку класс интервала — это наименьшее число, выбранное среди целого числа интервала и его инверсии, классы интервалов не могут быть инвертированы.

Классификация [ править ]

Интервалы можно описывать, классифицировать или сравнивать друг с другом по различным критериям.

$\макет { ширина линии = 60\мм отступ = 0\мм } \относительный с''{ \clef treble \time 3/1 \hide Staff.TimeSignature d,1 гс \бар "||" \перерыв \time 1/1 <d f> \bar "||" <d g> \bar "||" <f g> \bar "||" }$

Мелодические и гармонические интервалы

Мелодично-гармонический [ править ]

Интервал можно описать как

Вертикальный или гармонический , если две ноты звучат одновременно.
Горизонтальные, линейные или мелодичные , если они звучат последовательно. ^[2] Мелодические интервалы могут быть восходящими (низкий тон предшествует высокому) или нисходящим .

Диатонический и хроматический [ править ]

В общем,

Диатонический диатонической интервал — интервал, образованный двумя нотами гаммы .
Хроматический интервал — недиатонический интервал, образованный двумя нотами хроматической гаммы .

Восходящая и нисходящая хроматическая гамма C.

В таблице выше показаны 56 диатонических интервалов, образованных нотами гаммы до мажор (диатоническая гамма). Обратите внимание, что эти интервалы, как и любой другой диатонический интервал, также могут быть образованы нотами хроматической гаммы.

Различие между диатоническими и хроматическими интервалами является спорным, поскольку оно основано на определении диатонической гаммы, которая варьируется в литературе. Например, интервал B – E ♭ ( уменьшенная кварта , встречающаяся в гармонической гамме до-минор ) считается диатоническим, если гармонические минорные гаммы также считаются диатоническими. ^[12]В противном случае он считается хроматическим. Подробности смотрите в основной статье .

По общепринятому определению диатонической гаммы ^[б](исключая гармонический минор и мелодический минор ), все совершенные, мажорные и минорные интервалы являются диатоническими. И наоборот, никакой увеличенный или уменьшенный интервал не является диатоническим, за исключением увеличенной кварты и уменьшенной квинты.

А ♭ - мажорная гамма

Различие между диатоническими и хроматическими интервалами также может зависеть от контекста. Упомянутые выше 56 интервалов, образованных гаммой до-мажор, иногда называют диатоническими до-мажор . Все остальные интервалы называются хроматическими до мажор . Например, идеальная квинта A ♭ –E ♭ является хроматической по отношению к до мажор, потому что A ♭ и E ♭ не содержатся в гамме до мажор. он диатоничен Однако для других, например, для гаммы A ♭ мажор, .

Согласные и диссонансные [ править ]

Консонанс и диссонанс — относительные термины, обозначающие стабильность или состояние покоя определенных музыкальных эффектов. Диссонантные интервалы – это те, которые вызывают напряжение и желание разрешиться в согласные интервалы.

Эти термины относятся к использованию различных композиционных стилей.

В XV и XVI веках идеальные квинты и октавы, а также мажорные и малые трети и шестые считались гармонически согласными, а все остальные интервалы - диссонансными, включая идеальную кварту, которая к 1473 году была описана (Иоганнесом Тинкторисом ) как диссонансная, кроме верхних частей вертикальной звучности - например, с опорной третью внизу («6-3 аккорда»). ^[13]В период общепринятой практики имеет больше смысла говорить о согласных и диссонансных аккордах, и определенные интервалы, ранее считавшиеся диссонансными (например, минорные септимы), стали приемлемыми в определенных контекстах. Однако на протяжении всего этого периода начинающих музыкантов все еще обучали практике XVI века.
Герман фон Гельмгольц (1821–1894) предположил, что диссонанс вызывается наличием биений . ^[14] Гельмгольц далее считал, что биение, производимое верхними частями гармонических звуков, является причиной диссонанса в интервалах, слишком далеких друг от друга, чтобы вызвать биение между основными звуками . ^[15] Затем Гельмгольц отметил, что два гармонических тона, которые имеют общие низкие части, будут более созвучными, поскольку они производят меньше долей. ^[16]^[17] Гельмгольц игнорировал частичные звуки выше седьмой, так как считал, что они недостаточно слышны, чтобы иметь значительный эффект. ^[18] Исходя из этого, Гельмгольц классифицирует октаву, чистую квинту, идеальную кварту, большую шестую, большую треть и малую треть как согласные с уменьшающейся значимостью, а другие интервалы - как диссонансные.
Дэвид Коуп (1997) предлагает концепцию интервальной силы . ^[19]в котором сила, созвучие или стабильность интервала определяется его приближением к более низкому и более сильному или более высокому и более слабому положению в гармоническом ряду . См. Также: закон Липпса – Мейера и корень #Interval.

Все приведенные выше анализы относятся к вертикальным (одновременным) интервалам.

Простое и сложное [ править ]

Простой интервал — это интервал, охватывающий не более одной октавы (см. Основные интервалы выше). Интервалы, охватывающие более одной октавы, называются составными интервалами, поскольку их можно получить путем добавления одной или нескольких октав к простому интервалу ( см. Ниже ). подробности ^[20]

Шаги и пропуски [ править ]

Линейные (мелодические) интервалы можно описать как шаги или пропуски . Шаг , или сопряженное движение , ^[21]представляет собой линейный интервал между двумя последовательными нотами гаммы. Любой больший интервал называется пропуском (также называемым прыжком ), или дизъюнктным движением . ^[21] В гамме диатонической ^[б] шаг представляет собой либо второстепенную секунду (иногда также называемую полушагом ), либо большую секунду (иногда также называемую целым шагом ), при этом все интервалы второстепенной трети или больше пропускаются.

Например, от C до D (большая секунда) — это шаг, тогда как от C до E ( большая треть ) — это пропуск.

В более общем смысле, шаг — это меньший или более узкий интервал в музыкальной строке, а пропуск — это более широкий или больший интервал, где категоризация интервалов на шаги и пропуски определяется системой настройки и используемым пространством высоты тона .

Мелодическое движение , при котором интервал между любыми двумя последовательными тонами составляет не более шага или, менее строго, там, где пропуски редки, называется ступенчатым или слитным мелодическим движением, в отличие от скачкообразных или дизъюнктивных мелодических движений, характеризующихся частыми скачками.

Энгармонические интервалы [ править ]

Два интервала считаются энгармоническими или энгармонически эквивалентными , если они оба содержат одинаковые высоты звука , написанные по-разному; то есть, если ноты в двух интервалах сами по себе энгармонически эквивалентны. Энгармонические интервалы охватывают одинаковое количество полутонов .

Например, все четыре интервала, перечисленные в таблице ниже, энгармонически эквивалентны, поскольку ноты F ♯ и G ♭ обозначают одинаковую высоту звука, и то же самое верно для A ♯ и B ♭ . Все эти интервалы охватывают четыре полутона.

Число полутонов	Название интервала	Штатные должности
Число полутонов	Название интервала	1	2	3	4
4	главная треть	F ♯		A ♯
4	главная треть		G ♭		B ♭
4	уменьшенная четвертая	F ♯			B ♭
4	вдвое увеличенная секунда		G ♭	A ♯

При игре на фортепианной клавиатуре как отдельные аккорды эти интервалы неразличимы для слуха, поскольку все они играются одними и теми же двумя клавишами. Однако в музыкальном контексте диатоническая функция нот, входящих в эти интервалы, совсем другая.

Обсуждение выше предполагает использование распространенной системы настройки, 12-тоновой равнотемперированной («12-ТЕТ»). Но в других исторических темпераментах среднего тона высота пар нот, таких как F ♯ и G ♭, может не обязательно совпадать. Эти две ноты энгармоничны в 12-TET, но могут быть не такими в другой системе настройки. В таких случаях образуемые ими интервалы также не будут энгармоническими. Например, в четверть-запятой означает один все четыре интервала, показанные в примере выше, будут разными.

Минутные интервалы [ править ]

Есть также ряд минутных интервалов, не встречающихся в хроматической гамме и не имеющих диатонической функции, которые имеют собственные названия. Их можно описать как микротоны , а некоторые из них можно также классифицировать как запятые , поскольку они описывают небольшие расхождения, наблюдаемые в некоторых системах настройки, между энгармонически эквивалентными нотами. В следующем списке размеры интервалов в центах являются приблизительными.

Пифагорейская запятая — это разница между двенадцатью правильно настроенными идеальными квинтами и семью октавами. Оно выражается соотношением частот 531441:524288 (23,5 цента).
Синтоническая запятая — это разница между четырьмя правильно настроенными идеальными квинтами и двумя октавами плюс мажорная треть. Оно выражается соотношением 81:80 (21,5 цента).
Септимальная запятая равна 64:63 (27,3 цента) и представляет собой разницу между пифагорейской или 3-предельной «7-й» и «гармонической 7-й».
Диезис . обычно используется для обозначения разницы между тремя правильно настроенными мажорными терциями и одной октавой Оно выражается соотношением 128:125 (41,1 цента). Однако его использовали для обозначения других небольших интервалов: см. в разделе «Диесис» . подробности
Диашизма — это разница между тремя октавами и четырьмя правильно настроенными чистыми квинтами плюс двумя правильно настроенными мажорными терциями. Оно выражается соотношением 2048:2025 (19,6 центов).
Раскол (также схизма ) — это разница между пятью октавами и восемью правильно настроенными квинтами плюс одна правильно настроенная мажорная треть. Оно выражается соотношением 32805:32768 (2,0 цента). В этом также разница между пифагорейскими и синтонными запятыми. (Раскольническая мажорная терция - это раскол, отличный от просто мажорной терции, восемью квинтами вниз и пятью октавами вверх, F ♭ в C.)
Клейсма — это разница между шестью малыми терциями и одной тритавой или идеальной двенадцатой терцией ( октава плюс чистая квинта с соотношением частот 15625:15552 (8,1 цента). ) ).
Септимальная клейсма — это величина, на которую две основные трети 5:4 и семеричная мажорная треть, или супермажорная треть, 9:7 превышают октаву. Соотношение 225:224 (7,7 цента).
Четверть тона равна половине ширины полутона , что составляет половину ширины целого тона . Он равен ровно 50 центам.

Сложные интервалы [ править ]

Сложный интервал – это интервал, занимающий более одной октавы. ^[20] И наоборот, интервалы, охватывающие не более одной октавы, называются простыми интервалами (см. Основные интервалы ниже).

В общем, составной интервал может определяться последовательностью или «стеком» двух или более простых интервалов любого типа. Например, мажорная десятая часть (две позиции персонала выше одной октавы), также называемая составной мажорной терцией , охватывает одну октаву плюс одну мажорную треть.

Любой составной интервал всегда можно разложить на одну или несколько октав плюс один простой интервал. Например, мажорную семнадцатую можно разложить на две октавы и одну мажорную треть, и именно по этой причине ее называют составной мажорной терцией, даже если она построена путем сложения четырех пятых.

Диатоническое число DN _c сложного интервала, образованного из n простых интервалов с диатоническими числами DN ₁ , DN ₂ , ..., DN _n , определяется:

DN_{c}=1+(DN_{1}-1)+(DN_{2}-1)+...+(DN_{n}-1),\

что также можно записать как:

DN_{c}=DN_{1}+DN_{2}+...+DN_{n}-(n-1),\

Качество составного интервала определяется качеством простого интервала, на котором он основан. Например, составная мажорная терция представляет собой мажорную десятую часть (1+(8-1)+(3-1) = 10) или мажорную семнадцатую часть (1+(8-1)+(8-1)+(3 −1) = 17), а составная чистая квинта — это чистая двенадцатая (1+(8−1)+(5−1) = 12) или чистая девятнадцатая (1+(8−1)+(8−1) )+(5−1) = 19). Обратите внимание, что две октавы — это пятнадцатая, а не шестнадцатая (1+(8−1)+(8−1) = 15). Аналогично, три октавы — это двадцать вторая (1+3×(8−1) = 22) и так далее.

Основные сложные интервалы [ править ]

Количество полутона	Минор, мажор, или идеальные интервалы	Короткий	Дополненная или уменьшенные интервалы	Короткий
12			Уменьшенная девятая	d9
13	Малая девятая	м9	Расширенная октава	А8
14	Майор девятый	М9	Уменьшенная десятая	d10
15	Малая десятая	м10	Дополненная девятая	А9
16	Основная десятая	М10	Уменьшенный одиннадцатый	д11
17	Идеальный одиннадцатый	P11	Дополненная десятая	А10
18			Уменьшено двенадцатое место	д12
18			Дополненная одиннадцатая	А11
19	Идеальная двенадцатая или Тритава	Р12	Уменьшенный тринадцатый	д13
20	Минор тринадцатый	м13	Дополненная двенадцатая	А12
21	Майор тринадцатый	М13	Уменьшенный четырнадцатый	д14
22	Минор четырнадцатый	м14	Дополненная тринадцатая	А13
23	Майор четырнадцатый	М14	Уменьшенный пятнадцатый	д15
24	Идеальная пятнадцатая или двойная октава	P15	Дополненная четырнадцатая	А14
25			Дополненная пятнадцатая	А15

Здесь также стоит упомянуть мажорную семнадцатую (28 полутонов) — интервал, превышающий две октавы, который можно считать кратным чистой квинты (7 полутонов), поскольку его можно разложить на четыре чистых квинты (7 × 4 = 28 полутонов). ), или две октавы плюс мажорная треть (12 + 12 + 4 = 28 полутонов). Интервалы, превышающие мажорную семнадцатую, встречаются редко, чаще всего их называют составными названиями, например «две октавы плюс пятая». ^[22] а не «19-й».

Интервалы в аккордах [ править ]

Аккорды представляют собой наборы из трех и более нот. Обычно их определяют как комбинацию интервалов, начинающихся с общей ноты, называемой основной нотой аккорда. Например, мажорное трезвучие — это аккорд, содержащий три ноты, определяемые основным тоном и двумя интервалами (мажорная треть и чистая квинта). даже одиночный интервал ( диаду ). Иногда аккордом считают ^[23] Аккорды классифицируются по качеству и количеству определяющих их интервалов.

Качество аккордов интервалов качество и

Основные качества аккорда — мажорный , минорный , увеличенный , уменьшенный , полууменьшенный и доминантный . Символы . , используемые для обозначения качества аккорда, аналогичны символам, используемым для обозначения качества интервала (см. Выше) Кроме того, + или aug используется для увеличения, ° или dim для уменьшения, ^ø для наполовину уменьшенного и dom для доминирующего (сам по себе символ − не используется для уменьшенного).

Вычисление интервалов компонентов из названий и символов аккордов [ править ]

Основные правила расшифровки названий или символов аккордов кратко изложены ниже. Более подробная информация приведена в Правилах декодирования названий и символов аккордов .

Для трехнотных аккордов ( трезвучий ) мажор или минор всегда относятся к интервалу терции над основной нотой , тогда как увеличенные и уменьшенные всегда относятся к интервалу квинты над основной нотой. То же самое справедливо и для соответствующих символов (например, Cm означает C ^m3, а C+ означает C ⁺⁵). Таким образом, термины третий и пятый и соответствующие символы 3 и 5 обычно опускаются. Это правило можно распространить на все виды аккордов. ^[с]при условии, что вышеупомянутые качества появляются сразу после основной ноты или в начале названия или символа аккорда. Например, в обозначениях аккордов Cm и Cm ⁷, m относится к интервалу m3, а 3 опускается. Когда эти качества не появляются сразу после основной ноты или в начале имени или символа, их следует считать качествами интервала , а не качествами аккорда. Например, в См ^М7( минорный мажорный септаккорд ), m — качество аккорда и относится к интервалу m3, а M — к интервалу M7. Если номер дополнительного интервала указан сразу после качества аккорда, качество этого интервала может совпадать с качеством аккорда (например, CM ⁷ = СМ ^М7). Однако это не всегда верно (например, Cm ⁶ = См ^М6, С+ ⁷ = С+ ^м7, СМ ¹¹ = СМ ^P11). ^[с] смотрите в основной статье . Дополнительную информацию
Без противоположной информации большая терция и совершенная квинта ( мажорное трезвучие подразумеваются ). Например, аккорд C представляет собой трезвучие до мажор, а имя до минор септаккорд (Cm ⁷) подразумевает второстепенную терцию по правилу 1, идеальную 5-ю по этому правилу и второстепенную 7-ю по определению (см. ниже). У этого правила есть одно исключение (см. следующее правило).
Когда пятый интервал уменьшен , третий должен быть второстепенным. ^[д] Это правило переопределяет правило 2. Например, Cdim ⁷ подразумевает уменьшенную 5-ю по правилу 1, второстепенную 3-ю по этому правилу и уменьшенную 7-ю по определению (см. ниже).
Имена и символы, которые содержат только номер простого интервала (например, «септаккорд») или основу аккорда и число (например, «седьмой до» или «до». ⁷) интерпретируются следующим образом:
- Если число равно 2, 4, 6 и т. д., аккорд является аккордом мажорного тона (например, C ⁶ = С ^М6 = С ^{добавить6}) и содержит, вместе с подразумеваемым мажорным трезвучием, дополнительную мажорную 2-ю , идеальную 4-ю или мажорную 6-ю ступень (см. названия и символы добавленных тональных аккордов ).
- Если число 7, 9, 11, 13 и т. д., аккорд является доминантным (например, C ⁷ = С ^дом7) и содержит вместе с подразумеваемым мажорным трезвучием один или несколько следующих дополнительных интервалов: минорный 7-й, мажорный 9-й, совершенный 11-й и мажорный 13-й (см. названия и символы септаккордов и расширенных аккордов ).
- Если число равно 5, аккорд (технически не аккорд в традиционном понимании, а диада ) является пауэр-аккордом . Играются только основной тон, чистая квинта и обычно октава.

В таблице указаны интервалы, содержащиеся в некоторых основных аккордах ( компонентных интервалах ), и некоторые символы, используемые для их обозначения. Качество интервала или цифры, выделенные жирным шрифтом, можно вывести из названия или символа аккорда, применив правило 1. В примерах символов C используется в качестве основного корня аккорда.

Основные аккорды		Интервалы компонентов
Имя	символов Примеры	Третий	Пятый	Седьмой
Мажорная триада	С	M3	П5
Мажорная триада	CM или Cmaj	M 3	П5
Минорное трезвучие	См или Cмин	m 3	П5
Дополненная триада	C+ или Кауг	M3	AА5
Уменьшенная триада	C ° или Cdim	m3	д 5
Доминантный септаккорд	С ⁷, или С ^дом7	M3	П5	м 7
Минорный септаккорд	См ⁷, или Cмин ⁷	m 3	П5	м 7
Мажорный септаккорд	СМ ⁷, или Cmaj ⁷	M 3	П5	М 7
Дополненный септаккорд	С+ ⁷, Ках ⁷, С ^{7 ♯ 5}, или С ^{7 авг5}	M3	AА5	м 7
Уменьшенный септаккорд	С ° ⁷или Cdim ⁷	m3	д 5	d 7
Полууменьшенный септаккорд	С ^ø⁷, См ^{7 ♭ 5}, или См ^7dim5	m3	д 5	м 7

Размер интервалов, используемых в разных системах настройки [ править ]

Количество полутона	Имя	5-предельная настройка (отношение шага)	Сравнение ширины интервала (в центах)
Количество полутона	Имя	5-предельная настройка (отношение шага)	5-предельная настройка	Пифагорейский тюнинг	1/4 – запятая имелся в виду	Равный темперамент
0	Идеальный унисон	1:1	0	0	0	0
1	Незначительная секунда	16:15 27:25	112 133	90	117	100
2	Главный второй	9:8 10:9	204 182	204	193	200
3	Малая треть	6:5 32:27	316 294	294 318	310 (волк) 269	300
4	Основная треть	5:4	386	408 384	386 (волк) 427	400
5	Идеальная четвертая	4:3 27:20	498 520	498 (волк) 522	503 (волк) 462	500
6	Дополненная четвертая Уменьшенная пятая часть	45:32 25:18	590 569	612 588	579 621	600
7	Идеальная пятая часть	3:2 40:27	702 680	702 (волк) 678	697 (волк) 738	700
8	Малая шестая	8:5	814	792	814	800
9	Майор шестой	5:3 27:16	884 906	906	890	900
10	Минорная седьмая	16:9 9:5	996 1018	996	1007	1000
11	Майор седьмой	15:8 50:27	1088 1067	1110	1083	1100
12	Идеальная октава	2:1	1200	1200	1200	1200

В этой таблице сравниваются ширины интервалов, используемые в четырех различных системах настройки. Для облегчения сравнения только интервалы , предусмотренные 5-предельной настройкой (см. симметричную шкалу № 1 ), выделены жирным шрифтом, а значения в центах округлены до целых чисел. Обратите внимание, что в каждой из неравных систем строя ширина каждого типа интервала (включая полутон) по определению меняется в зависимости от ноты, с которой начинается интервал. Это искусство именно интонации . При равном темпераменте интервалы никогда не совпадают точно друг с другом. Такова цена использования равноотстоящих интервалов в 12-тоновой шкале. Для простоты для некоторых типов интервалов в таблице указано только одно значение ( наиболее часто наблюдаемое ).

В 1 ⁄ - запятая означала , что по определению 11 чистых пятых имеют размер примерно 697 центов (700 − ε центов, где ε ≈ 3,42 цента); так как средний размер 12 квинт должен равняться ровно 700 центам (как при равном темпераменте), то другой должен иметь размер около 738 центов (700 + 11 ε , волчья квинта или уменьшенная шестая ); 8 основных терций имеют размер около 386 центов (400 − 4 ε ), 4 имеют размер около 427 центов (400 + 8 ε , фактически уменьшенные кварты ), а их средний размер составляет 400 центов. Короче говоря, аналогичные различия в ширине наблюдаются для всех типов интервалов, кроме унисонов и октав, и все они кратны ε (разница между 1 / 4 -запятая означала одну пятую и среднюю пятую). Более подробный анализ представлен на сайте 1/4 - запятая означает размер интервалов . 1 ⁄ - запятая означает, что тон был создан для получения только основных третей, но только 8 из них являются простыми (5:4, около 386 центов).

Пифагорейская настройка характеризуется меньшими различиями, поскольку они кратны меньшему ε ( ε ≈ 1,96 цента, разница между пифагорейской квинтой и средней квинтой). Обратите внимание, что здесь квинта шире 700 центов, тогда как у большинства средних темпераментов , в том числе 1 ⁄ - запятая означает, что она сокращена до размера меньше 700. Более подробный анализ представлен в разделе Пифагорейская настройка § Размер интервалов .

Система настройки с 5 лимитами использует в качестве строительных блоков только тона и полутона, а не набор идеальных квинт, и это приводит к еще большему разнообразию интервалов по всей гамме (каждый тип интервала имеет три или четыре разных размера). Более детальный анализ представлен при 5-предельной настройке § Размер интервалов . 5-лимитная настройка была разработана для максимизации количества справедливых интервалов, но даже в этой системе некоторые интервалы не являются простыми (например, 3 квинты, 5 больших терций и 6 малых терций не являются справедливыми; кроме того, 3 мажорных и 3 малых терции являются неполными). волчьи интервалы ).

Вышеупомянутая симметричная гамма 1, определенная в 5-предельной системе настройки, не является единственным методом получения только интонации . Можно построить более точные интервалы или просто интервалы, более близкие к равнотемперным эквивалентам, но большинство из перечисленных выше исторически использовались в эквивалентных контекстах. В частности, асимметричная версия 5-предельной шкалы настройки обеспечивает более точное значение минорной седьмой части (9:5, а не 16:9). Более того, тритон (увеличенная кварта или уменьшенная квинта) мог иметь и другие справедливые соотношения; например, 7:5 (около 583 центов) или 17:12 (около 603 центов) являются возможными альтернативами увеличенной кварты (последнее довольно распространено, поскольку оно ближе к равномерному значению в 600 центов). Интервал 7:4 (около 969 центов), также известный как гармоническая седьмая часть , был спорным вопросом на протяжении всей истории теории музыки; это на 31 цент более лестно, чем равнотемперированная минорная седьмая часть. Для получения дополнительной информации об эталонных соотношениях см. 5-предельную настройку § Самые справедливые соотношения. .

В диатонической системе каждый интервал имеет один или несколько энгармонических эквивалентов , например, увеличенную секунду для малой терции .

Интервальный корень [ править ]

Хотя интервалы обычно обозначаются относительно их нижней ноты, Дэвид Коуп ^[19] и Хиндемит ^[24]оба предполагают концепцию интервального корня . Чтобы определить корень интервала, нужно найти его ближайшее приближение в гармоническом ряду. Таким образом, корень идеальной кварты является ее верхней нотой, поскольку это октава основного тона в гипотетическом гармоническом ряду. Нижняя нота всех нечетных интервалов с диатонической нумерацией является корнем, как и вершина всех четных интервалов. Таким образом, корень набора интервалов или аккорда определяется интервальным корнем его самого сильного интервала.

Что касается его полезности, Коуп ^[19]представляет собой пример финального тонического аккорда некоторой популярной музыки, который традиционно анализируется как «субмедиантный аккорд шесть-пять» ( добавленные шестые аккорды по популярной терминологии) или первый инверсный септаккорд (возможно, доминанта срединного V / iii) . В соответствии с интервальным тоном самого сильного интервала аккорда (в первом обращении, CEGA), идеальная квинта (C – G) является нижней до, тоникой.

Интервальные циклы [ править ]

Интервальные циклы «разворачивают [т. е. повторяют] один повторяющийся интервал в серии, которая завершается возвратом к исходному классу высоты тона», и обозначены Джорджем Перлом буквой «C» для обозначения цикла с классом интервала. целое число, чтобы отличить интервал. Таким образом, уменьшенный септаккорд будет C3, а увеличенное трезвучие — C4. Можно добавить верхний индекс, чтобы различать транспозиции, используя цифры 0–11 для обозначения самого низкого класса высоты тона в цикле. ^[25]

Альтернативные соглашения об именах интервалов [ править ]

Как показано ниже, некоторые из вышеупомянутых интервалов имеют альтернативные названия, а некоторые из них принимают конкретное альтернативное имя в пифагорейской настройке , пятипредельной настройке или системах настройки темперамента с значком, например, с четвертью запятой . Все интервалы с приставкой полуторный- настроены правильно , а их отношение частот , представленное в таблице, представляет собой сверхчастичное число (или эпиморное отношение). То же самое справедливо и для октавы.

Обычно запятая — это уменьшенная секунда, но это не всегда так (подробнее см. Альтернативные определения запятой ). Например, в пифагорейской настройке уменьшенная секунда представляет собой нисходящий интервал (524288:531441, или около -23,5 цента), а пифагорейская запятая является его противоположностью (531441:524288, или около 23,5 цента). 5-предельная настройка определяет четыре вида запятых , три из которых соответствуют определению уменьшенной секунды и, следовательно, перечислены в таблице ниже. Четвертая, называемая синтонной запятой (81:80), не может рассматриваться ни как уменьшенная секунда, ни как ее противоположность. см. в разделе «Уменьшение секунд при 5-предельной настройке» Дополнительную информацию .

Количество полутона	Общие имена				Конкретные имена
	Качество и количество		Другое соглашение об именах		Пифагорова настройка	5-предельная настройка	1/4 – запятая имелся в виду
	Полный	Короткий	Другое соглашение об именах		Пифагорова настройка	5-предельная настройка	1/4 – запятая имелся в виду
0	идеальный унисон или идеальное простое число	П1
	уменьшенная секунда	d2			нисходящий Пифагорова запятая (524288:531441)	менее острый (128:125)
	уменьшенная секунда	d2			нисходящий Пифагорова запятая (524288:531441)	диашизма (2048:2025) больший диезис (648:625)
1	второстепенная секунда	м2	полутон , полутона, полшага	диатонический полутон, мажорный полутон	клей (256:243)
1	расширенный унисон или дополненное простое число	А1	полутон , полутона, полшага	хроматический полутон, минорный полутон	апотом (2187:2048)
2	главная секунда	М2	тон, целый тон , целый шаг		полоктавы (9:8)
3	малая треть	m3				полуторный (6:5)
4	главная треть	M3				полуторный (5:4)
5	идеальная четвертая	П4			шесть третей (4:3)
6	уменьшенная пятая часть	d5	тритон ^[а]
6	дополненная четвертая	A4	тритон ^[а]
7	идеальная пятая часть	П5			половина (3:2)
12	идеальная октава	Р8			дуплекс (2:1)

Кроме того, в некоторых культурах мира есть свои собственные названия интервалов, встречающихся в их музыке. Например, 22 вида интервалов, называемых шрути канонически определены в индийской классической музыке .

Латинская номенклатура [ править ]

До конца XVIII века латынь использовалась в качестве официального языка по всей Европе для научных и музыкальных учебников. В музыке многие английские термины произошли от латыни. Например, полутон происходит от латинского полутонуса .

Префикс полу- обычно используется здесь для обозначения «более короткого», а не «половинного». ^[26]^[27]^[28]А именно, полутонус, полудитонус, семидиатессарон, полудиапенте, полугексахордум, полугептахордум или полудиапазон короче соответствующего целого интервала на один полутон. Например, полудитон (3 полутона, или около 300 копеек) — это не половина дитона (4 полутона, или около 400 копеек), а укороченный на один полутон дитон. Более того, в пифагорейском строе (наиболее распространенной системе строя до XVI века) полутритон (d5) меньше тритона (А4) на одну пифагорейскую запятую (около четверти полутона).

Количество полутона	Качество и количество	Короткий	латинский номенклатура
0	Идеальный унисон	П1	унисон
1	Незначительная секунда	м2	полутон
1	Расширенный унисон	А1	ненужный унисон
2	Главный второй	М2	тонны
2	Уменьшенная треть	д3
3	Малая треть	m3	полутон
3	Дополненная секунда	А2	ненужный тон
4	Основная треть	M3	дитонический
4	Уменьшенный четвертый	d4	полудиатессарон
5	Идеальная четвертая	П4	диатессарон
5	Дополненная треть	А3	лишний дитонус
6	Уменьшенная пятая часть	d5	полудиапенте, полутритонус
6	Дополненная четвертая	A4	тритон
7	Идеальная пятая часть	П5	диапанте
7	Уменьшенная шестая позиция	d6	полугексахорд
8	Малая шестая	м6	меньше гексахорда, полутон мажор с диапенте, тетратон
8	Дополненная пятая	А5	совершенно лишний
9	Майор шестой	М6	мажорный гексахорд, тон с диапенте
9	Уменьшенный седьмой	d7	полугептахорда
10	Минорная седьмая	м7	меньше гептахорды, полутона с диапентой, пентатона
10	Дополненная шестая	А6	лишние гексахорды
11	Майор седьмой	М7	мажорный гептахорд, дитон с диапенте
11	Уменьшенная октава	d8	полудиапазон
12	Идеальная октава	Р8	камертон
12	Дополненная седьмая	A7	лишние гептахорды

Недиатонические интервалы [ править ]

Интервалы в недиатонических гаммах можно называть, используя аналоги названий диатонических интервалов, используя диатонический интервал аналогичного размера и различая его путем изменения качества или путем добавления других модификаторов. Например, справедливый интервал 7/6 можно назвать субмалой терцией , поскольку его ширина ~ 267 центов, что уже, чем второстепенная терция (300 центов в 12-TET, ~ 316 центов для справедливого интервала 6/). 5), или как семеричную малую терцию , поскольку это семипредельный интервал. Эти названия относятся только к размеру отдельного интервала, и номер интервала не обязательно соответствует количеству ступеней шкалы (гептатонической) шкалы. Это наименование особенно распространено в интонационных и микротональных гаммах. ^[29]

Наиболее распространенными из этих расширенных качеств являются нейтральный интервал между минорным и мажорным интервалом; и субминорные и супермажорные интервалы , соответственно уже минорного интервала или шире мажорного интервала. Точный размер таких интервалов зависит от системы настройки, но часто они отличаются от размеров диатонических интервалов примерно на четверть тона (50 центов, половина хроматического шага). Например, нейтральная секунда , характерный интервал арабской музыки , в 24-TET составляет 150 центов, ровно на полпути между малой и большой секундами. прогрессию В совокупности они дают уменьшенную, субминорную, минорную, нейтральную, мажорную, супермажорную , увеличенную для секунд, третей, шестых и седьмых. Это соглашение об именах может быть расширено до унисонов, четвертых, пятых и октав с помощью sub и super , в результате чего прогрессия уменьшена, суб, совершенна, супер, увеличена . Это позволяет называть все интервалы в 24-TET или 31-TET, последний из которых использовал Адриан Фоккер . Различные дополнительные расширения используются в Ксенгармоническая музыка . ^[29]

Интервалы высоты тона [ править ]

В посттональной или атональной теории, первоначально разработанной для равнотемперированной европейской классической музыки, написанной с использованием двенадцатитоновой техники или сериализма , часто используется целочисленная запись , особенно в теории музыкальных множеств . В этой системе интервалы называются по количеству полушагов от 0 до 11, при этом наибольший класс интервалов равен 6.

В атональной или музыкальной теории множеств существует множество типов интервалов, первым из которых является упорядоченный интервал высоты тона , расстояние между двумя высотами звука вверх или вниз. Например, интервал от C вверх до G равен 7, а интервал от G вниз до C равен −7. Можно также измерить расстояние между двумя звуками без учета направления с помощью неупорядоченного интервала высоты звука, чем-то похожего на интервал в теории тонов.

Интервал между классами высоты звука может измеряться с помощью упорядоченных и неупорядоченных интервалов классов высоты звука. Упорядоченный интервал, также называемый направленным интервалом, можно рассматривать как меру вверх, которая, поскольку мы имеем дело с классами высоты звука, зависит от того, какая высота выбрана равной 0. Для неупорядоченных интервалов класса высоты см. класс интервала . ^[30]

Общие и специальные интервалы [ править ]

В диатонической теории множеств различают и родовые интервалы конкретные . Конкретные интервалы — это класс интервалов или количество полутонов между шагами гаммы или элементами коллекции, а общие интервалы — это количество шагов диатонической гаммы (или позиций нотоносца) между нотами коллекции или гаммы.

Обратите внимание, что позиции нотного стана, когда они используются для определения обычного номера интервала (второго, третьего, четвертого и т. д.), подсчитываются с учетом позиции нижней ноты интервала, тогда как общие номера интервалов подсчитываются без учета этой позиции. Таким образом, общие номера интервалов меньше на 1 по сравнению с обычными номерами интервалов.

Сравнение [ править ]

Конкретный интервал		Общий интервал	Диатоническое имя
Количество полутонов	Интервальный класс	Общий интервал	Диатоническое имя
0	0	0	Идеальный унисон
1	1	1	Незначительная секунда
2	2	1	Главный второй
3	3	2	Малая треть
4	4	2	Основная треть
5	5	3	Идеальная четвертая
6	6	3 4	Дополненная четвертая Уменьшенная пятая часть
7	5	4	Идеальная пятая часть
8	4	5	Малая шестая
9	3	5	Майор шестой
10	2	6	Минорная седьмая
11	1	6	Майор седьмой
12	0	7	Идеальная октава

Обобщения и использование без подачи [ править ]

Термин «интервал» также можно распространить на другие музыкальные элементы, помимо высоты звука. Дэвида Левина интервал В книге «Обобщенные музыкальные интервалы и трансформации» используется как общая мера расстояния между моментами времени , тембрами или более абстрактными музыкальными явлениями. ^[31]^[32]

Например, все еще ощутим интервал между двумя колоколообразными звуками, не имеющими высоты тона. Когда два тона имеют схожие акустические спектры (наборы частиц), интервал представляет собой всего лишь расстояние сдвига спектра тона вдоль оси частот, поэтому привязка к высоте звука как к контрольным точкам не требуется. Тот же принцип, естественно, применим и к высоким тонам (со схожим гармоническим спектром), а это означает, что интервалы можно воспринимать «напрямую», без распознавания высоты звука. Этим, в частности, объясняется преобладание интервального слуха над абсолютным слухом. ^[33]^[34]

См. также [ править ]

Примечания [ править ]

^ Перейти обратно: ^а ^б Термин тритон иногда используется более строго как синоним увеличенной кварты (А4).
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Выражение «диатоническая гамма» здесь строго определяется как 7-тоновая гамма , которая представляет собой либо последовательность последовательных натуральных нот (таких как гамма до мажор , C–D–E–F–G–A–B или нота A). - минорная гамма , A–B–C–D–E–F–G) или любое ее транспонирование . Другими словами, гамма, которую можно написать семью последовательными нотами без случайностей на нотоносце с обычной тональностью или без подписи. Сюда входят, например, мажорные и натуральные минорные гаммы, но не включаются некоторые другие семитоновые гаммы, такие как мелодический минор и гармонический минор (см. также Диатонические и хроматические гаммы ).
^ Перейти обратно: ^а ^б Общее правило 1 обеспечивает согласованность интерпретации таких символов, как CM. ⁷, См ⁶и С+ ⁷. Некоторые музыканты обоснованно предпочитают думать, что в CM ⁷, M относится к седьмому, а не к третьему. Этот альтернативный подход правомерен, поскольку и третий, и седьмой являются основными, но он противоречив, поскольку подобная интерпретация невозможна для Cm. ⁶ и С+ ⁷ (в см ⁶, m не может относиться к шестому, который является старшим по определению, и в C+ ⁷, + не может относиться к седьмому, который является второстепенным). Оба подхода раскрывают только один из интервалов (М3 или М7) и требуют других правил для выполнения задачи. Каким бы ни был метод декодирования, результат один и тот же (например, CM ⁷всегда традиционно декодируется как C–E–G–B, подразумевая M3, P5, M7). Преимущество правила 1 состоит в том, что оно не имеет исключений, что делает его самым простым из возможных подходов к декодированию качества аккордов.

Согласно этим двум подходам, некоторые могут отформатировать мажорный септаккорд как CM. ⁷ (общее правило 1: M относится к M3), а другие как C ^М7(альтернативный подход: M относится к M7). К счастью, даже С. ^М7 становится совместимым с правилом 1, если оно считается аббревиатурой CM ^М7, в котором первая буква M опущена. Опущенное М является качеством третьего и выводится согласно правилу 2 (см. выше), в соответствии с интерпретацией простого символа С, который по тому же правилу обозначает СМ.
^ Все трезвучия представляют собой тертические аккорды (аккорды, определяемые последовательностями терций), и основная треть в этом случае будет давать нетретовый аккорд. А именно, уменьшенная квинта охватывает 6 полутонов от основного тона, поэтому ее можно разложить на последовательность из двух малых терций , каждая из которых охватывает 3 полутона (m3 + m3), что совместимо с определением терцианного аккорда. Если бы использовалась мажорная треть (4 полутона), это повлекло бы за собой последовательность, содержащую мажорную секунду (M3 + M2 = 4 + 2 полутона = 6 полутонов), что не соответствовало бы определению терцианного аккорда.

Ссылки [ править ]

^ Праут, Эбенезер (1903), «Я-Введение», Гармония, ее теория и практика (30-е издание, исправленное и в значительной степени переписанное издание), Лондон: Огенер; Бостон: Boston Music Co., стр. 1, ISBN 978-0781207836
^ Перейти обратно: ^а ^б Линдли, Марк; Кэмпбелл, Мюррей; Великий, Клайв (2001). «Интервал». В Сэди, Стэнли ; Тиррелл, Джон (ред.). Словарь музыки и музыкантов New Grove (2-е изд.). Лондон: Издательство Macmillan . ISBN 978-1-56159-239-5 . ‎
^ Олдуэлл, Э.; Шахтер, К.; Кадвалладер, А. (11 марта 2010 г.), «Часть 1: Основные материалы и процедуры, Часть 1», Гармония и голосовое руководство (4-е изд.), Ширмер, стр. 8, ISBN 978-0495189756
^ Даффин, Росс В. (2007), «3. Настройка без клавиатуры», Как равный темперамент разрушил гармонию (и почему вас это должно волновать) (1-е изд.), WW Norton, ISBN 978-0-393-33420-3
^ «Prime (ii). См. Unison» , Grove Music Online . Издательство Оксфордского университета. По состоянию на август 2013 г. (требуется подписка) )
^ Бурштейн, Л. Паунди; Штраус, Джозеф Н. (2016). Краткое введение в тональную гармонию (1-е изд.). Нью-Йорк: WW Нортон. п. 55. ИСБН 978-0-393-26476-0 .
^ Перейти обратно: ^а ^б ^с Лайтц, Стивен Г. (2016). Полный музыкант: комплексный подход к теории, анализу и прослушиванию (4-е изд.). Нью-Йорк: Издательство Оксфордского университета . стр. 27–31. ISBN 9780199347094 .
^ Перейти обратно: ^а ^б Костка, Стефан; Пейн, Дороти; Альмен, Байрон (2018). Тональная гармония, введение в посттональную музыку (8-е изд.). Нью-Йорк: МакГроу Хилл . стр. 16–18. ISBN 9781259447099 .
^ Перейти обратно: ^а ^б Определение совершенного созвучия из Вебер, Годфри (1841). Общий учитель музыки . идеальное согласие
^ Костка, Стефан ; Пейн, Дороти (2008). Тональная гармония , с. 21. Первое издание, 1984 г.
^ Праут, Эбенезер (1903). Гармония: ее теория и практика , 16-е издание. Лондон: Augener & Co. (перепечатка факса, Сент-Клер Шорс, Мичиган: Scholarly Press, 1970), стр. 10. ISBN 0-403-00326-1 .
^ См., например, Уильям Лавлок, Рудименты музыки (Нью-Йорк: St Martin's Press; Лондон: Дж. Белл, 1957): ^{[ нужна страница ]}, перепечатано в 1966, 1970 и 1976 годах Дж. Беллом, в 1971 году издательством St Martins Press, в 1981, 1984 и 1986 годах, Лондон: Bell & Hyman. ISBN 9780713507447 (пбк). ISBN 9781873497203
^ Драбкин, Уильям (2001). «Четвертый». Словарь музыки и музыкантов New Grove , второе издание, под редакцией Стэнли Сэди и Джона Тиррелла . Лондон: Макмиллан.
^ Гельмгольц 1895 , с. 172: «Резкость при одновременном звучании двух тонов зависит… от количества ударов, производимых в секунду».
^ Гельмгольц 1895 , с. 178: «Причину этого явления следует искать в долях, создаваемых высокими верхними частями таких сложных тонов».
^ Гельмгольц 1895 , с. 182.
^ Гельмгольц, Герман Л.Ф. Об ощущениях тона как теоретической основе теории музыки , 2-е английское издание, перевод Эллиса, Александра Дж. (1885), переиздано Dover Publications с новым введением (1954). ISBN 0-486-60753-4 , с. 182d: «Подобно тому, как совпадения двух первых верхних частичных тонов привели нас к естественным созвучиям Октавы и Квинты, совпадения более высоких верхних частичных тонов привели бы нас к дальнейшей серии естественных созвучий».
^ Гельмгольц 1895 , с. 183: «Здесь я остановился, потому что 7-й частичный тон полностью устранен или, по крайней мере, значительно ослаблен».
^ Перейти обратно: ^а ^б ^с Коуп, Дэвид (1997). Техники современного композитора , стр. 40–41. Нью-Йорк, Нью-Йорк: Книги Ширмера. ISBN 0-02-864737-8 .
^ Перейти обратно: ^а ^б Вятт, Кейт ; Шредер, Карл (1998). Гармония и теория . Корпорация Хэла Леонарда . п. 77. ИСБН 9780793579914 .
^ Перейти обратно: ^а ^б Бондс, Марк Эван (2006). История музыки в западной культуре , стр.123. 2-е изд. ISBN 0-13-193104-0 .
^ Айкин, Джим (2004). Руководство для исполнителя по аккордам и гармонии: теория музыки для реальных музыкантов , с. 24. ISBN 0-87930-798-6 .
^ Каройи, Отто (1965), Знакомство с музыкой , с. 63. Хаммондсворт (Англия) и Нью-Йорк: Penguin Books. ISBN 0-14-020659-0 .
^ Хиндемит, Пол (1934). Мастерство музыкальной композиции . Нью-Йорк: Associated Music Publishers. Цитируется в Коупе (1997), с. 40–41.
^ Перл, Джордж (1990). Слушающий композитор , с. 21. Калифорния: Издательство Калифорнийского университета. ISBN 0-520-06991-9 .
^ Джозеффо Зарлино, Le Istitutioneharmiche... в которой, помимо предметов, принадлежащих к музыке, заявлены многие места Поэтов, Историков и Философов, как можно ясно видеть при их чтении (Венеция, 1558): 162 .
^ JF Niermeyer [ de ] , Mediae latinitatis lexicon minus: Lexique latin médiéval – français/anglais: Средневековый латинско-французский/английский словарь , сокращения и указатель источников, составленный К. ван де Кифтом с помощью GSMM Lake-Schoonebeek ( Лейден: Э. Дж. Брилл, 1976): 955. ISBN 90-04-04794-8 .
^ Роберт Де Хэндло: Правила и Йоханнес Ханбойс, Сумма: новый критический текст и перевод Теория греческой и латинской музыки 7 (Линкольн: University of Nebraska Press, 1991): 193fn17. ISBN 0803279345 .
^ Перейти обратно: ^а ^б «Имена расширенно-диатонических интервалов» . Ксенгармоническая вики .
^ Редер, Джон (2001). «Интервальный класс». В Сэди, Стэнли ; Тиррелл, Джон (ред.). Словарь музыки и музыкантов New Grove (2-е изд.). Лондон: Издательство Macmillan . ISBN 978-1-56159-239-5 . ‎
^ Левин, Дэвид (1987). Обобщенные музыкальные интервалы и трансформации , например разделы 3.3.1 и 5.4.2. Нью-Хейвен: Издательство Йельского университета. Перепечатано издательством Оксфордского университета, 2007 г. ISBN 978-0-19-531713-8
^ Окельфорд, Адам (2005). Повторение в музыке: теоретические и метатеоретические перспективы , с. 7. ISBN 0-7546-3573-2 . «Левин постулирует понятие музыкальных «пространств», состоящих из элементов, между которыми мы можем интуитивно уловить «интервалы».... Левин приводит ряд примеров музыкальных пространств, включая диатоническую гамму тонов, расположенных в скалярном порядке; 12 тонов. классы с одинаковым темпераментом; последовательность моментов времени, пульсирующих на регулярных временных расстояниях с интервалом в одну единицу времени, и семейство длительностей, каждая из которых измеряет временной интервал в единицах времени ... предлагаются преобразования тембра, происходящие из изменений в; спектр частичных..."
^ Тангиан (Тангиан), Андраник (1993). Искусственное восприятие и распознавание музыки . Конспект лекций по искусственному интеллекту. Том. 746. Берлин-Гейдельберг: Шпрингер. ISBN 978-3-540-57394-4 .
^ Тангиан (Тангиан), Андраник (1994). «Принцип корреляции восприятия и его применение к распознаванию музыки». Музыкальное восприятие . 11 (4): 465–502. дои : 10.2307/40285634 . JSTOR 40285634 .

Источники [ править ]

Гельмгольц, HLF фон (1895) [1877]. Об ощущениях звука как теоретической основе теории музыки . Перевод Александра Джона Эллиса (3-е английское изд.). Лонгманс, Грин и Ко.

Внешние ссылки [ править ]

[TritoneA4-6] Перейти обратно: ^а ^б Термин тритон иногда используется более строго как синоним увеличенной кварты (А4).

[diatonic-9] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Выражение «диатоническая гамма» здесь строго определяется как 7-тоновая гамма , которая представляет собой либо последовательность последовательных натуральных нот (таких как гамма до мажор , C–D–E–F–G–A–B или нота A). - минорная гамма , A–B–C–D–E–F–G) или любое ее транспонирование . Другими словами, гамма, которую можно написать семью последовательными нотами без случайностей на нотоносце с обычной тональностью или без подписи. Сюда входят, например, мажорные и натуральные минорные гаммы, но не включаются некоторые другие семитоновые гаммы, такие как мелодический минор и гармонический минор (см. также Диатонические и хроматические гаммы ).

[rule1-26] Перейти обратно: ^а ^б Общее правило 1 обеспечивает согласованность интерпретации таких символов, как CM. ⁷, См ⁶и С+ ⁷. Некоторые музыканты обоснованно предпочитают думать, что в CM ⁷, M относится к седьмому, а не к третьему. Этот альтернативный подход правомерен, поскольку и третий, и седьмой являются основными, но он противоречив, поскольку подобная интерпретация невозможна для Cm. ⁶ и С+ ⁷ (в см ⁶, m не может относиться к шестому, который является старшим по определению, и в C+ ⁷, + не может относиться к седьмому, который является второстепенным). Оба подхода раскрывают только один из интервалов (М3 или М7) и требуют других правил для выполнения задачи. Каким бы ни был метод декодирования, результат один и тот же (например, CM ⁷всегда традиционно декодируется как C–E–G–B, подразумевая M3, P5, M7). Преимущество правила 1 состоит в том, что оно не имеет исключений, что делает его самым простым из возможных подходов к декодированию качества аккордов.

Согласно этим двум подходам, некоторые могут отформатировать мажорный септаккорд как CM. ⁷ (общее правило 1: M относится к M3), а другие как C ^М7(альтернативный подход: M относится к M7). К счастью, даже С. ^М7 становится совместимым с правилом 1, если оно считается аббревиатурой CM ^М7, в котором первая буква M опущена. Опущенное М является качеством третьего и выводится согласно правилу 2 (см. выше), в соответствии с интерпретацией простого символа С, который по тому же правилу обозначает СМ.

[rule4-27] Все трезвучия представляют собой тертические аккорды (аккорды, определяемые последовательностями терций), и основная треть в этом случае будет давать нетретовый аккорд. А именно, уменьшенная квинта охватывает 6 полутонов от основного тона, поэтому ее можно разложить на последовательность из двух малых терций , каждая из которых охватывает 3 полутона (m3 + m3), что совместимо с определением терцианного аккорда. Если бы использовалась мажорная треть (4 полутона), это повлекло бы за собой последовательность, содержащую мажорную секунду (M3 + M2 = 4 + 2 полутона = 6 полутонов), что не соответствовало бы определению терцианного аккорда.

[1] Праут, Эбенезер (1903), «Я-Введение», Гармония, ее теория и практика (30-е издание, исправленное и в значительной степени переписанное издание), Лондон: Огенер; Бостон: Boston Music Co., стр. 1, ISBN 978-0781207836

[LindleyMarkCampbell-2] Перейти обратно: ^а ^б Линдли, Марк; Кэмпбелл, Мюррей; Великий, Клайв (2001). «Интервал». В Сэди, Стэнли ; Тиррелл, Джон (ред.). Словарь музыки и музыкантов New Grove (2-е изд.). Лондон: Издательство Macmillan . ISBN 978-1-56159-239-5 . ‎

[3] Олдуэлл, Э.; Шахтер, К.; Кадвалладер, А. (11 марта 2010 г.), «Часть 1: Основные материалы и процедуры, Часть 1», Гармония и голосовое руководство (4-е изд.), Ширмер, стр. 8, ISBN 978-0495189756

[4] Даффин, Росс В. (2007), «3. Настройка без клавиатуры», Как равный темперамент разрушил гармонию (и почему вас это должно волновать) (1-е изд.), WW Norton, ISBN 978-0-393-33420-3

[prime-5] «Prime (ii). См. Unison» , Grove Music Online . Издательство Оксфордского университета. По состоянию на август 2013 г. (требуется подписка) )

[7] Бурштейн, Л. Паунди; Штраус, Джозеф Н. (2016). Краткое введение в тональную гармонию (1-е изд.). Нью-Йорк: WW Нортон. п. 55. ИСБН 978-0-393-26476-0 .

[:0-8] Перейти обратно: ^а ^б ^с Лайтц, Стивен Г. (2016). Полный музыкант: комплексный подход к теории, анализу и прослушиванию (4-е изд.). Нью-Йорк: Издательство Оксфордского университета . стр. 27–31. ISBN 9780199347094 .

[:1-10] Перейти обратно: ^а ^б Костка, Стефан; Пейн, Дороти; Альмен, Байрон (2018). Тональная гармония, введение в посттональную музыку (8-е изд.). Нью-Йорк: МакГроу Хилл . стр. 16–18. ISBN 9781259447099 .

[Weber-11] Перейти обратно: ^а ^б Определение совершенного созвучия из Вебер, Годфри (1841). Общий учитель музыки . идеальное согласие

[12] Костка, Стефан ; Пейн, Дороти (2008). Тональная гармония , с. 21. Первое издание, 1984 г.

[13] Праут, Эбенезер (1903). Гармония: ее теория и практика , 16-е издание. Лондон: Augener & Co. (перепечатка факса, Сент-Клер Шорс, Мичиган: Scholarly Press, 1970), стр. 10. ISBN 0-403-00326-1 .

[14] См., например, Уильям Лавлок, Рудименты музыки (Нью-Йорк: St Martin's Press; Лондон: Дж. Белл, 1957): ^{[ нужна страница ]}, перепечатано в 1966, 1970 и 1976 годах Дж. Беллом, в 1971 году издательством St Martins Press, в 1981, 1984 и 1986 годах, Лондон: Bell & Hyman. ISBN 9780713507447 (пбк). ISBN 9781873497203

[15] Драбкин, Уильям (2001). «Четвертый». Словарь музыки и музыкантов New Grove , второе издание, под редакцией Стэнли Сэди и Джона Тиррелла . Лондон: Макмиллан.

[FOOTNOTEHelmholtz1895p._172:_"The_roughness_from_sounding_two_tones_together_depends..._the_number_of_beats_produced_in_a_second."-16] Гельмгольц 1895 , с. 172: «Резкость при одновременном звучании двух тонов зависит… от количества ударов, производимых в секунду».

[FOOTNOTEHelmholtz1895p._178:_"The_cause_of_this_phenomenon_must_be_looked_for_in_the_beats_produced_by_the_high_upper_partials_of_such_compound_tones"-17] Гельмгольц 1895 , с. 178: «Причину этого явления следует искать в долях, создаваемых высокими верхними частями таких сложных тонов».

[FOOTNOTEHelmholtz1895182-18] Гельмгольц 1895 , с. 182.

[19] Гельмгольц, Герман Л.Ф. Об ощущениях тона как теоретической основе теории музыки , 2-е английское издание, перевод Эллиса, Александра Дж. (1885), переиздано Dover Publications с новым введением (1954). ISBN 0-486-60753-4 , с. 182d: «Подобно тому, как совпадения двух первых верхних частичных тонов привели нас к естественным созвучиям Октавы и Квинты, совпадения более высоких верхних частичных тонов привели бы нас к дальнейшей серии естественных созвучий».

[FOOTNOTEHelmholtz1895p._183:_"Here_I_have_stopped,_because_the_7th_partial_tone_is_entirely_eliminated,_or_at_least_much_weakened."-20] Гельмгольц 1895 , с. 183: «Здесь я остановился, потому что 7-й частичный тон полностью устранен или, по крайней мере, значительно ослаблен».

[Cope-21] Перейти обратно: ^а ^б ^с Коуп, Дэвид (1997). Техники современного композитора , стр. 40–41. Нью-Йорк, Нью-Йорк: Книги Ширмера. ISBN 0-02-864737-8 .

[compound-22] Перейти обратно: ^а ^б Вятт, Кейт ; Шредер, Карл (1998). Гармония и теория . Корпорация Хэла Леонарда . п. 77. ИСБН 9780793579914 .

[Bonds-23] Перейти обратно: ^а ^б Бондс, Марк Эван (2006). История музыки в западной культуре , стр.123. 2-е изд. ISBN 0-13-193104-0 .

[24] Айкин, Джим (2004). Руководство для исполнителя по аккордам и гармонии: теория музыки для реальных музыкантов , с. 24. ISBN 0-87930-798-6 .

[Otto-25] Каройи, Отто (1965), Знакомство с музыкой , с. 63. Хаммондсворт (Англия) и Нью-Йорк: Penguin Books. ISBN 0-14-020659-0 .

[28] Хиндемит, Пол (1934). Мастерство музыкальной композиции . Нью-Йорк: Associated Music Publishers. Цитируется в Коупе (1997), с. 40–41.

[Perle-29] Перл, Джордж (1990). Слушающий композитор , с. 21. Калифорния: Издательство Калифорнийского университета. ISBN 0-520-06991-9 .

[30] Джозеффо Зарлино, Le Istitutioneharmiche... в которой, помимо предметов, принадлежащих к музыке, заявлены многие места Поэтов, Историков и Философов, как можно ясно видеть при их чтении (Венеция, 1558): 162 .

[31] JF Niermeyer [ de ] , Mediae latinitatis lexicon minus: Lexique latin médiéval – français/anglais: Средневековый латинско-французский/английский словарь , сокращения и указатель источников, составленный К. ван де Кифтом с помощью GSMM Lake-Schoonebeek ( Лейден: Э. Дж. Брилл, 1976): 955. ISBN 90-04-04794-8 .

[32] Роберт Де Хэндло: Правила и Йоханнес Ханбойс, Сумма: новый критический текст и перевод Теория греческой и латинской музыки 7 (Линкольн: University of Nebraska Press, 1991): 193fn17. ISBN 0803279345 .

[xen-extended-33] Перейти обратно: ^а ^б «Имена расширенно-диатонических интервалов» . Ксенгармоническая вики .

[34] Редер, Джон (2001). «Интервальный класс». В Сэди, Стэнли ; Тиррелл, Джон (ред.). Словарь музыки и музыкантов New Grove (2-е изд.). Лондон: Издательство Macmillan . ISBN 978-1-56159-239-5 . ‎

[35] Левин, Дэвид (1987). Обобщенные музыкальные интервалы и трансформации , например разделы 3.3.1 и 5.4.2. Нью-Хейвен: Издательство Йельского университета. Перепечатано издательством Оксфордского университета, 2007 г. ISBN 978-0-19-531713-8

[36] Окельфорд, Адам (2005). Повторение в музыке: теоретические и метатеоретические перспективы , с. 7. ISBN 0-7546-3573-2 . «Левин постулирует понятие музыкальных «пространств», состоящих из элементов, между которыми мы можем интуитивно уловить «интервалы».... Левин приводит ряд примеров музыкальных пространств, включая диатоническую гамму тонов, расположенных в скалярном порядке; 12 тонов. классы с одинаковым темпераментом; последовательность моментов времени, пульсирующих на регулярных временных расстояниях с интервалом в одну единицу времени, и семейство длительностей, каждая из которых измеряет временной интервал в единицах времени ... предлагаются преобразования тембра, происходящие из изменений в; спектр частичных..."

[Tanguiane1993-37] Тангиан (Тангиан), Андраник (1993). Искусственное восприятие и распознавание музыки . Конспект лекций по искусственному интеллекту. Том. 746. Берлин-Гейдельберг: Шпрингер. ISBN 978-3-540-57394-4 .

[Tangian1994-38] Тангиан (Тангиан), Андраник (1994). «Принцип корреляции восприятия и его применение к распознаванию музыки». Музыкальное восприятие . 11 (4): 465–502. дои : 10.2307/40285634 . JSTOR 40285634 .

[1]

[2]

[3]

[4]

[5]

[а]

[6]

[7]

[б]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[с]

[д]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

v т Это Созвучие и диссонанс
Argument Avoid note Beating Cadence Chord Interval Musical note Nonchord tone Cambiata Changing tones Pedal point Preparation Resolution Spectra
Consonances	Unison Minor third Major third Perfect fourth Perfect fifth Minor sixth Major sixth Octave
Dissonances	Minor second Major second Tritone Minor seventh Major seventh
List of musical intervals