Пятипредельная настройка

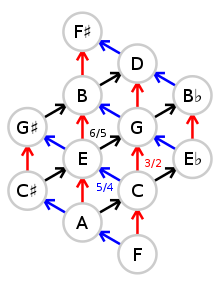
Настройка с пятью пределами , настройка с пятью пределами или настройка с пятью простыми пределами (не путать с настройкой с пятью нечетными пределами ) — это любая система настройки , музыкального инструмента которая получает частоту каждой ноты путем умножения частоты. данной справочной ноты (базовой ноты) на произведения целых степеней 2, 3 или 5 ( простые числа ограничены 5 или меньше), например 2 ⁻³·3 ¹·5 ¹ = 15/8 .

Степени 2 представляют интервальные движения по октавам. Степени 3 представляют собой движения с интервалами в полные квинты (плюс одну октаву, которую можно удалить, умножив на 1/2, т. е. 2). ⁻¹). Степени 5 представляют собой интервалы больших терций (плюс две октавы, которые можно удалить умножением на 1/4, т. е. 2 ⁻²). Таким образом, 5-лимитные настройки полностью состоят из суммирования трех основных чисто настроенных интервалов (октав, терций и квинт). Поскольку восприятие созвучия, по-видимому, связано с низкими числами в гармоническом ряду, а 5-предельная настройка опирается на три самых низких простых числа, 5-предельная настройка должна быть способна создавать очень согласные гармонии. Следовательно, настройка на 5 пределов считается методом получения именно интонации .

Количество потенциальных интервалов, классов высоты тона, высоты тона, центров тональности, аккордов и модуляций, доступных для 5-предельных настроек, не ограничено, поскольку никакая (ненулевая целая) степень любого простого числа не равна любой степени любого другого простого числа, поэтому доступные интервалы могут Можно представить, что оно простирается бесконечно в трехмерной решетке (одно измерение или одно направление для каждого простого числа). Если октавы игнорируются, их можно рассматривать как двумерную решетку классов высоты звука (названий нот), простирающуюся бесконечно в двух направлениях.

Однако большинство систем настройки, предназначенных для акустических инструментов, ограничивают общее количество тонов по практическим соображениям. Также типично (но не всегда) иметь одинаковое количество высот в каждой октаве, что представляет собой транспозицию октав фиксированного набора классов высоты звука. В этом случае систему настройки можно также рассматривать как октавно-повторяющуюся шкалу с определенным количеством тонов на октаву.

Частоту любого тона в конкретной 5-предельной системе настройки можно получить путем умножения частоты фиксированного эталонного тона, выбранного для системы настройки (например, A440 , A442, A432, C256 и т. д.), на некоторую комбинацию степеней. 3 и 5 для определения класса высоты звука и некоторую степень 2 для определения октавы.

Например, если у нас есть система настройки с 5 пределами, в которой базовая нота — C256 (это означает, что она имеет 256 циклов в секунду, и мы решили назвать ее C), то f _C = 256 Гц, или «частота C равна 256 Гц. ." Есть несколько способов определить E выше этого C. Используя терции, можно подняться на один фактор 5 и уменьшить на два фактора 2, достигнув соотношения частот 5/4, или, используя квинты, можно подняться на четыре раза по 3 и уменьшить на шесть раз. коэффициенты 2, достигая 81/64. Частоты становятся:

f_{E}=5^{1}\cdot 3^{0}\cdot 2^{-2}\cdot f_{C}={5 \over 4}\cdot 256\ \mathrm {Hz} =320\ \mathrm {Hz}

или

f_{E}=5^{0}\cdot 3^{4}\cdot 2^{-6}\cdot f_{C}={81 \over 64}\cdot 256\ \mathrm {Hz} =324\ \mathrm {Hz}

Диатоническая гамма

Предполагая, что мы ограничимся семью классами высоты звука (семь нот на октаву), можно настроить знакомую диатоническую гамму, используя 5-предельную настройку несколькими способами, каждый из которых делает большинство трезвучий идеально настроенными, согласными и стабильными. насколько это возможно, но оставьте некоторые триады в менее стабильных интервальных конфигурациях.

Выдающиеся ноты данной гаммы настроены так, что их частоты образуют отношения относительно небольших целых чисел. Например, в тональности соль мажор соотношение частот нот G и D ( чистая квинта ) составляет 3/2, а соотношение частот нот G и C — 2/3 (нисходящая чистая квинта) или 4/. 3 ( идеальная кварта ) идет вверх, а основная треть от G до B равна 5/4.

Справедливую диатоническую гамму можно получить следующим образом. Представив тональность до мажор, предположим, мы настаиваем на том, чтобы субдоминантный корень F и доминантный корень G находились на расстоянии одной квинты (3:2) от тонического корня C с обеих сторон, а аккорды FAC, CEG и GBD были просто мажорными. триады (с соотношением частот 4:5:6):

Тон	Имя	С		Д		И		Ф		Г		А		Б		С
	Соотношение	1/1		9/8		5/4		4/3		3/2		5/3		15/8		2/1
	Естественный	24		27		30		32		36		40		45		48
	центы	0		204		386		498		702		884		1088		1200

Шаг	Интервал		Т		т		с		Т		т		Т		с
	Соотношение		9/8		10/9		16/15		9/8		10/9		9/8		16/15
	Шаг центов		204		182		112		204		182		204		112

Это известно как интенсивная диатоническая гамма Птолемея . Здесь строка, озаглавленная «Натуральный», выражает все эти отношения, используя общий список натуральных чисел (путем умножения строки выше на 1см ее знаменателей). Другими словами, наименьшее появление этой формы однооктавной гаммы в гармоническом ряду представляет собой подмножество 7 из 24 гармоник, находящихся в октаве от гармоник с 24 по 48.

Три основные трети правильные (5:4), а три второстепенные трети такие же, как и ожидалось (6:5), но от D до F - это полудитон или пифагорейская минорная треть (равная трем нисходящим просто идеальным квинтам с поправкой на октаву) , синтоническая запятая уже, чем правильно настроенная второстепенная треть (6:5).

Как следствие, мы получаем шкалу, в которой EGB и ACE являются всего лишь второстепенными триадами (10:12:15), но триада DFA не имеет той минорной формы или звука, которую мы могли бы ожидать, будучи (27:32:40) . Более того, триада BDF не является уменьшенной триадой (25:30:36) , которую мы получили бы, сложив две второстепенные терции 6:5, а представляет собой (45:54:64): ^[1]^[2]

Видно, что появляются основные ступенчатые интервалы шкалы:

с = 16:15 ( полутон )
т = 10:9 ( минорный тон )
Т = 9:8 ( мажорный тон )

которые могут быть объединены для формирования более крупных интервалов (среди прочего):

Ц = 6:5 (малая треть)
Тт = 5:4 (большая треть)
Ттс = 4:3 (идеальная четвёртая)
ТТц = 3:2 (идеальная пятая часть)
ТТТтссс 2:1 (октава)

Другой способ сделать это заключается в следующем. Думая в относительной минорной тональности ля минор и используя D, A и E в качестве квинты, мы можем утверждать, что аккорды DFA, ACE и EGB представляют собой всего лишь минорные трезвучия (10:12:15):

Тон	Имя	А		Б		С		Д		И		Ф		Г		А
	Соотношение	1/1		9/8		6/5		4/3		3/2		8/5		9/5		2/1
	Естественный	120		135		144		160		180		192		216		240
	центы	0		204		316		498		702		814		1018		1200

Шаг	Интервал		Т		с		т		Т		с		Т		т
	Соотношение		9/8		16/15		10/9		9/8		16/15		9/8		10/9
	Шаг центов		204		112		182		204		112		204		182

Если мы сравним это с более ранней гаммой, мы увидим, что для пяти пар последовательных нот соотношения шагов остаются прежними, но в одной ноте, D, шаги CD и DE поменяли свои соотношения.

Три основные трети по-прежнему составляют 5:4, а три второстепенные трети по-прежнему составляют 6:5, а четвертая - 32:27, за исключением того, что теперь BD вместо DF составляет 32:27. FAC и CEG по-прежнему образуют лишь мажорные триады (4:5:6), но теперь это GBD (108:135:160), а теперь BDF (135:160:192).

Есть и другие возможности, такие как повышение A вместо понижения D, но каждая корректировка нарушает что-то еще.

Очевидно, невозможно получить одновременно все семь диатонических трезвучий в конфигурации (4:5:6) для мажора, (10:12:15) для минора и (25:30:36) для уменьшенных, если ограничимся семью веревками.

Это демонстрирует необходимость увеличения количества нот для достижения желаемых гармоний.

Двенадцатитоновая шкала

Чтобы построить двенадцатитоновую гамму при пятипредельной настройке, мы начнем с построения таблицы, содержащей пятнадцать правильно интонируемых звуков:

Фактор	1 ⁄ 9	1 ⁄ 3	1	3 ⁄ 1	9 ⁄ 1
5 ⁄ 1	Д- 10/9 182 ^[3]	А 5/3 884	И 5/4 386	Б 15/8 1088	F ♯ + 45/32 590 ^[3]	примечание соотношение центы
1	B ♭ − 16/9 996 ^[3]	Ф 4/3 498	С 1 0	Г 3/2 702	Д 9/8 204	примечание соотношение центы
1 ⁄ 5	G ♭ − 64/45 610 ^[3]	D ♭ − 16/15 112 ^[3]	A ♭ 8/5 814	E ♭ 6/5 316	B ♭ 9/5 1018	примечание соотношение центы

Множители, перечисленные в первой строке и первом столбце, представляют собой степени 3 и 5 соответственно (например, 1 ⁄ 9 = 3 ⁻²). Цветами обозначены пары энгармонических нот почти одинаковой высоты. Все соотношения выражены относительно C в центре этой диаграммы (базовая нота для этой шкалы). Они рассчитываются в два этапа:

Для каждой ячейки таблицы базовый коэффициент получается путем умножения соответствующих коэффициентов. Например, базовое соотношение для нижней левой ячейки составляет 1/9 · 1/5 = 1/45.
Затем базовое соотношение умножается на отрицательную или положительную степень 2, настолько большую, насколько это необходимо, чтобы привести его в диапазон октавы, начиная с C (от 1/1 до 2/1). Например, базовое соотношение для нижней левой ячейки (1/45) умножается на 2. ⁶, и полученное соотношение составит 64/45, что представляет собой число от 1/1 до 2/1.

Обратите внимание, что степени двойки, используемые на втором этапе, можно интерпретировать как возрастающую или нисходящую октаву . Например, умножив частоту ноты на 2. ⁶ означает увеличение его на 6 октав. При этом каждую строку таблицы можно рассматривать как последовательность квинт (по возрастанию вправо), а каждый столбец — как последовательность больших терций (по возрастанию вверх). Например, в первой строке таблицы находится восходящая квинта от D и A, а также еще одна (за которой следует нисходящая октава) от A до E. Это предполагает альтернативный, но эквивалентный метод вычисления тех же отношений. Например, вы можете получить A (соотношение 5/3), начиная с C, переместив одну ячейку влево и одну вверх по таблице, что означает снижение на одну пятую (2/3) и повышение на одну большую треть ( 5/4):

{1 \over 1}\cdot {2 \over 3}\cdot {5 \over 4}={10 \over 12}={5 \over 6}.

Поскольку это ниже C, вам нужно подняться на октаву, чтобы попасть в желаемый диапазон соотношений (от 1/1 до 2/1):

{5 \over 6}\cdot {2 \over 1}={10 \over 6}={5 \over 3}.

12-тоновая гамма получается удалением одной ноты на каждую пару энгармонических нот. Это можно сделать по крайней мере тремя способами, общим для которых является удаление G ♭ в соответствии с соглашением, действительным даже для пифагорейских шкал на основе C и средних шкал с 1/4 запятой. Обратите внимание, что это уменьшенная квинта , примерно на полоктавы, выше тона C, которая представляет собой дисгармонический интервал; кроме того, его соотношение имеет самые большие значения в числителе и знаменателе среди всех тонов шкалы, что делает его наименее гармоничным: есть причины избегать его.
Первая стратегия, которую мы здесь условно обозначим как симметричная шкала 1 , состоит в выделении для удаления тонов в левом верхнем и правом нижнем углах таблицы. Второй, обозначенный как симметричная гамма 2 , заключается в отбрасывании нот в первой и последней ячейке второго ряда (с пометкой « 1 »). Третий, обозначаемый как асимметричный масштаб , состоит в отбрасывании первого столбца (с пометкой « 1/9 »). Полученные 12-тоновые гаммы показаны ниже:

Симметричный масштаб 1
Фактор	1 ⁄ 9	1 ⁄ 3	1	3	9
5		А 5/3	И 5/4	Б 15/8	F ♯ + 45/32
1	B ♭ − 16/9	Ф 4/3	С 1	Г 3/2	Д 9/8
1 ⁄ 5		D ♭ − 16/15	A ♭ 8/5	E ♭ 6/5

Симметричный масштаб 2
Фактор	1 ⁄ 9	1 ⁄ 3	1	3	9
5	Д- 10/9	А 5/3	И 5/4	Б 15/8	F ♯ + 45/32
1		Ф 4/3	С 1	Г 3/2
1 ⁄ 5		D ♭ − 16/15	A ♭ 8/5	E ♭ 6/5	B ♭ 9/5

Асимметричная шкала
Фактор	1 ⁄ 9	1 ⁄ 3	1	3	9
5		А 5/3	И 5/4	Б 15/8	F ♯ + 45/32
1		Ф 4/3	С 1	Г 3/2	Д 9/8
1 ⁄ 5		D ♭ − 16/15	A ♭ 8/5	E ♭ 6/5	B ♭ 9/5

В первой и второй гамме B ♭ и D являются точной инверсией друг друга. Для третьего это не так. По этой причине эти две гаммы считаются симметричными (хотя удаление G ♭ делает все 12 тоновых гамм, включая те, которые создаются с помощью любой другой системы настройки, слегка асимметричными).

Асимметричная система имеет то преимущество, что имеет «самые справедливые» соотношения (содержащие меньшие числа), девять чистых квинт (фактор 3/2), восемь чистых мажорных терций (коэффициент 5/4), а также шесть чистых второстепенных терций (коэффициент 3/2) . коэффициент 6/5). Однако он также содержит две нечистые квинты (например, от D до A — 40/27, а не 3/2) и три нечистые второстепенные трети (например, от D до F — 32/27, а не 6/5), что практически ограничивает модуляцию. узкому диапазону клавиш. Аккорды тоники C, доминанты G и субдоминанты F чистые, а также D ♭ , A ♭ , E ♭ и минорные аккорды Fm, Cm, Gm, Am, Bm и Em, но не Dm.

Недостатком асимметричной системы является то, что она дает 14 волчьих интервалов, а не 12, как симметричные.

B ♭ в первой симметричной гамме отличается от B ♭ в других шкалах синтонной запятой и составляет более 21 цента. В одинаково темперированных гаммах разница устраняется за счет того, что все ступени имеют одинаковое соотношение частот.

Асимметричная шкала, построенная путем суммирования частотных коэффициентов 2/1 (синий), 3/2 (зеленый) и 5/4 (коричневый) в логарифмическом масштабе.

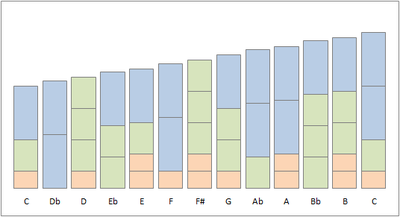Построение асимметричной шкалы графически показано на рисунке. Каждый блок имеет высоту в центах конструктивных отношений частот 2/1, 3/2 и 5/4. Можно распознать повторяющиеся закономерности. Например, во многих случаях следующая нота создается путем замены блока 5/4 и блока 3/2 на блок 2/1, что представляет собой соотношение 16/15.

Аналогичное изображение, построенное с использованием частотных коэффициентов 2, 3 и 5, а не 2/1, 3/2 и 5/4, смотрите здесь .

Справедливые соотношения

Справедливые соотношения, использованные для построения этих шкал, можно использовать как ориентир для оценки созвучия интервалов в других шкалах (например, см. эту сравнительную таблицу ). Однако 5-лимитная настройка — не единственный способ получить только интонацию . Можно построить просто интервалы с еще более «справедливыми» соотношениями или, альтернативно, со значениями, более близкими к равнотемперированным эквивалентам. Например, настройка с семью пределами иногда используется, чтобы получить немного более точный и, следовательно, более согласный интервал для малой септимы (7/4) и ее инверсии, мажорной секунды (8/7). Список этих эталонных соотношений, которые можно назвать чистыми или строго справедливыми интервалами или соотношениями, представлен ниже:

Название интервала	Короткий	Количество полутона	5-предельная настройка				7-ми предельная настройка	17-лимитная настройка
			Симметричные весы		Асимметричные весы
			№ 1	№ 2	Стандартный	Расширенный
Идеальный унисон	П1	0	1/1	1/1	1/1	1/1	1/1	1/1
Незначительная секунда	м2	1	16/15	16/15	16/15	16/15	15/14	14/13
Главный второй	М2	2	9/8	10/9	9/8	9/8	8/7	8/7
Малая треть	m3	3	6/5	6/5	6/5	6/5	6/5	6/5
Основная треть	M3	4	5/4	5/4	5/4	5/4	5/4	5/4
Идеальная четвертая	П4	5	4/3	4/3	4/3	4/3	4/3	4/3
Дополненная четвертая	A4	6	45/32	45/32	45/32	25/18	7/5	05.07 или 17.12.
Уменьшенная пятая часть	d5	6	64/45	64/45	64/45	36/25	10/7	7.10 или 24.17
Идеальная пятая часть	П5	7	3/2	3/2	3/2	3/2	3/2	3/2
Малая шестая	м6	8	8/5	8/5	8/5	8/5	8/5	8/5
Майор шестой	М6	9	5/3	5/3	5/3	5/3	5/3	5/3
Минорная седьмая	м7	10	16/9	9/5	9/5	9/5	7/4	7/4
Майор седьмой	М7	11	15/8	15/8	15/8	15/8	15/8	13/7
Идеальная октава	Р8	12	2/1	2/1	2/1	2/1	2/1	2/1

Ячейки, выделенные желтым цветом, обозначают более точные интервалы, чем интервалы в неокрашенных ячейках в той же строке. Те, что выделены голубым, указывают на еще более справедливые соотношения.

Обратите внимание, что соотношения 45/32 и 64/45 для тритонов (увеличенная кварта и уменьшенная квинта) не во всех контекстах считаются строго справедливыми, но они являются наиболее справедливыми из возможных в вышеупомянутых 5-предельных шкалах настройки. Расширенная асимметричная 5-предельная шкала (см. ниже) обеспечивает несколько более точные соотношения для обоих тритонов (25/18 и 36/25), чистота которых также вызывает споры. Настройка с семью пределами позволяет использовать максимально оптимальные соотношения, а именно 7/5 (около 582,512 центов, также известный как септимальный тритон ) и 10/7 (около 617,488 центов). Эти соотношения более созвучны, чем 17/12 (около 603 000 центов) и 24/17 (около 597 000 центов), которые можно получить при настройке на 17 пределов, однако последние также довольно распространены, поскольку они ближе к равным. умеренная стоимость 600.000 центов.

Вышеупомянутый интервал 7/4 (около 968,826 центов), также известный как септимальная минорная септима или гармоническая септима, был спорным вопросом на протяжении всей истории теории музыки; это на 31 цент более лестно, чем равнотемперированная минорная седьмая часть.

Размер интервалов

В таблицах выше показаны только соотношения частот каждой ноты по отношению к базовой ноте. можно определить двенадцать интервалов Однако интервалы могут начинаться с любой ноты, поэтому для каждого типа интервала — двенадцать унисонов, двенадцать полутонов , двенадцать двухполутоновых интервалов и т. д.

В 5-предельной настройке каждый тип интервала, за исключением унисонов и октав, имеет три или четыре разных размера. Это цена, которую приходится платить за поиск именно интонации. В таблице справа показаны их соотношения частот для асимметричной шкалы: отклонения окрашены в цвет, а отклонения, соответствующие волчьим интервалам, выделены фиолетовым цветом. Отклонения возникают потому, что ноты определяют четыре разных полутона :

S_{1}={{5 \over 4}\div {6 \over 5}}={25 \over 24}\approx 70.672\ {\hbox{cents}}

(«Просто» расширенный унисон между E ♭ и E)

S_{2}={{9 \over 8}\div {16 \over 15}}={135 \over 128}\approx 92.179\ {\hbox{cents}}

(Дополненный унисон между D ♭ и D)

S_{3}={16 \over 15}\approx 111.731\ {\hbox{cents}}

(«Просто» второстепенная секунда между C и D ♭ )

S_{4}={{9 \over 5}\div {5 \over 3}}={27 \over 25}\approx 133.238\ {\hbox{cents}}

(Незначительная секунда между A и B ♭ )

Напротив, в одинаково темперированной хроматической гамме все полутона измеряются

S_{E}={\sqrt[{12}]{2}}=100.000{\text{ cents}}

и интервалы любого типа имеют одинаковый размер, но ни один из них не настроен правильно, за исключением унисонов и октав.

Запятые

В других системах настройки запятая может определяться как минутный интервал, равный разнице между двумя видами полутонов (диатоническим и хроматическим, также известным как малая секунда, m2 , или увеличенный унисон, A1 ). Однако в этом случае образуются 4 вида полутонов (два A1, S ₁ и S ₂ и два m2, S ₃ и S ₄ ), а 12 различных запятых можно определить как разницу между их размерами в центах или, что то же самое, как соотношения между их соотношениями. Среди них мы выбираем шесть по возрастанию (те, у которых соотношение больше 1/1 и положительный размер в центах):

Название запятой	Эквивалентные определения		Размер
Название запятой	В смысле темперамент	В 5-лимитном тюнинге (асимметричный масштаб)	Соотношение	центы
Диашизма ( DS )	${m2 \over A1}$ через 1/6 запятой означало одно	${S_{3} \over S_{2}}={{16 \over 15}\div {135 \over 128}}$	${2048 \over 2025}$	$19.6~$
Синтонная запятая ( SC )	${{LD} \over {DS}}={{GD} \over {LD}}$	${S_{2} \over S_{1}}={{135 \over 128}\div {25 \over 24}}$	${81 \over 80}$	$21.5~$
Синтонная запятая ( SC )	${{LD} \over {DS}}={{GD} \over {LD}}$	${S_{4} \over S_{3}}={{27 \over 25}\div {16 \over 15}}$	${81 \over 80}$	$21.5~$
Малый диезис ( МД )	${m2 \over A1}$ через 1/4 запятой имелось в виду	${S_{3} \over S_{1}}={{16 \over 15}\div {25 \over 24}}$	${128 \over 125}$	$41.1~$
Малый диезис ( МД )	${m2 \over A1}$ через 1/4 запятой имелось в виду	${S_{4} \over S_{2}}={{27 \over 25}\div {135 \over 128}}$	${128 \over 125}$	$41.1~$
Большой диезис ( БГ )	${m2 \over A1}$ через 1/3 запятой имелось в виду	${S_{4} \over S_{1}}={{27 \over 25}\div {25 \over 24}}$	${648 \over 625}$	$62.6~$

Остальные шесть отношений отбрасываются, поскольку они прямо противоположны этим и, следовательно, имеют точно такую же длину, но противоположное направление (т. е. нисходящее направление, соотношение меньше 1/1 и отрицательный размер в центах). . Мы получаем запятые четырех разных размеров: диашизма, малая диезис, синтонная запятая и большая диезис. Поскольку S ₁ ( просто A1 ) и S ₃ ( просто m2 ) являются наиболее часто встречающимися полутонами в этой 12-тоновой гамме (см. таблицы выше), то меньший диезис, определяемый как соотношение между ними, является наиболее часто встречающимся. заметил запятую.

Синтоническая запятая также определяется в 5-предельной настройке как соотношение между основным тоном (M2 с размером 9/8) и второстепенным тоном (M2 с размером 10/9). Обратите внимание, что в других системах настройки его нельзя определить как соотношение между диатоническими и хроматическими полутонами (м2/А1), но это важное эталонное значение, используемое для настройки идеальной квинты в любой системе настройки в синтоническом континууме темперамента (включая также имел в виду один темперамент).

Уменьшенные секунды

Три из вышеупомянутых запятых, а именно диашизма, диезис и большой диезис, соответствуют определению уменьшенной секунды , являясь разницей между размерами в центах диатонического и хроматического полутона (или, что то же самое, соотношением между их частотами). соотношения).

Напротив, синтоническая запятая определяется либо как разница в центах между двумя хроматическими полутонами (S ₂ и S ₁ ), либо между двумя диатоническими полутонами (S ₄ и S ₃ ), и не может считаться уменьшенной секундой.

Расширение двенадцатитоновой гаммы

В приведенной выше таблице для построения базовых соотношений используются только низкие степени 3 и 5. Однако его можно легко расширить, используя более высокие положительные и отрицательные степени тех же чисел, например 5. ² = 25, 5 ⁻² = 1/25, 3 ³ = 27 или 3 ⁻³ = 1/27. Комбинируя эти базовые соотношения, можно получить шкалу с 25, 35 или даже более шагами.

Например, можно получить 35 шагов, добавляя строки в каждом направлении следующим образом:

Фактор		1/9	1/3	1	3	9
125	примечание соотношение центы	A ♯ 125/72 955.0 ^[3]	E ♯ 125/96 457.0	B ♯ 125/64 1158.9	Ф + 375/256 660.9 ^[3]	С + 1125/1024 162.9 ^[3]
25	примечание соотношение центы	F ♯ 25/18 568.7 ^[3]	C ♯ 25/24 70.7	G ♯ 25/16 772.6	D ♯ 75/64 274.6	A ♯ + 225/128 976.5 ^[3]
5	примечание соотношение центы	Д- 10/9 182.4	А 5/3 884.4	И 5/4 386.3	Б 15/8 1088.3	F ♯ + 45/32 590.2
1	примечание соотношение центы	B ♭ − 16/9 996.1	Ф 4/3 498.0	С 1/1 0.0	Г 3/2 702.0	Д 9/8 203.9
1/5	примечание соотношение центы	G ♭ − 64/45 609.8	D ♭ − 16/15 111.7	A ♭ 8/5 813.7	E ♭ 6/5 315.6	B ♭ 9/5 1017.6
1/25	примечание соотношение центы	И − 256/225 223.5 ^[3]	Б − 128/75 925.4 ^[3]	F ♭ 32/25 427.4	C ♭ 48/25 1129.3	G ♭ 36/25 631.3
1/125	примечание соотношение центы	С − 2048/1125 1037.1 ^[3]	Г − 512/375 539.1 ^[3]	Д − 128/125 41.1 ^[3]	А 192/125 743.0	И 144/125 245.0

Левый столбец ( 1/9 ) иногда удаляется (как в асимметричной шкале, показанной выше), создавая таким образом асимметричную таблицу с меньшим количеством шагов. Обратите внимание, что для уменьшенной квинты получается более точное соотношение (CG ♭ = 36/25) по сравнению с описанной выше ограниченной 5-лимитной настройкой (где от C до G ♭ - = 64/45). ^[4]

История

В пифагорейской настройке, возможно, первой системе настройки, теоретизированной на Западе, ^[5] единственными очень согласными интервалами были чистая квинта и ее инверсия, идеальная кварта . Пифагорейская мажорная терция (81:64) и минорная терция (32:27) были диссонансными , и это мешало музыкантам использовать трезвучия и аккорды , заставляя их на протяжении веков писать музыку с относительно простой фактурой . В позднем Средневековье музыканты поняли, что, слегка смягчая высоту некоторых нот, пифагорейские терции можно сделать созвучными . Например, если вы уменьшите синтонную запятую (81:80), частота E, CE (большая треть) и EG (малая треть) станет справедливой. А именно, CE сужается до справедливо интонированного соотношения

{81 \over 64}\cdot {80 \over 81}={{1\cdot 5} \over {4\cdot 1}}={5 \over 4}

и в то же время EG расширяется до справедливого соотношения

{32 \over 27}\cdot {81 \over 80}={{2\cdot 3} \over {1\cdot 5}}={6 \over 5}

Недостаток в том, что квинты AE и EB, сглаживая E, становятся почти такими же диссонирующими, как квинта пифагорейского волка . Но пятая CG остается созвучной, поскольку только E сглажена (CE * EG = 5/4 * 6/5 = 3/2) и может использоваться вместе с CE для получения до- мажорного трезвучия (CEG).

Обобщая это простое обоснование, Джозеффо Зарлино в конце шестнадцатого века создал первую правильно интонируемую 7-тоновую ( диатоническую ) гамму, которая содержала чистые совершенные квинты (3:2), чистые мажорные терции и чистые минорные терции:

F → A → C → E → G → B → D

Это последовательность только больших терций (M3, соотношение 5:4) и только второстепенных терций (m3, соотношение 6:5), начиная с F:

Ф + М3 + м3 + М3 + м3 + М3 + м3

Поскольку M3 + m3 = P5 (идеальная квинта), т. е. 5/4 * 6/5 = 3/2, это в точности эквивалентно диатонической гамме, полученной в 5-предельной простой интонации, и, следовательно, может рассматриваться как подмножество таблица построения, используемая для 12-тоновой ( хроматической ) гаммы:

А	→	И	→	Б
↑		↑		↑
Ф	→	С	→	Г	→	Д

где обе строки представляют собой последовательности только квинт, а FA, CE, GB — это только основные трети:

M3		M3		M3
+		+		+
Ф	+	П5	+	П5	+	П5

См. также

Примечания

^ Райт, Дэвид (2009). Математика и музыка , стр. 140–141. ISBN 978-0-8218-4873-9 .
^ Джонстон, Бен и Гилмор, Боб (2006). «Система обозначений для расширенной простой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , с. 78. ISBN 978-0-252-03098-7 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот Джон Фонвилл . «Расширенная справедливая интонация Бена Джонстона - Руководство для переводчиков», стр. 113–114, « Перспективы новой музыки» , том. 29, нет. 2 (лето 1991 г.), стр. 106–137.
^ Примечания от G ♯ до D ♭ взяты из Дона Майкла Рэндела , Гарвардский музыкальный словарь , 4-е издание. Кембридж, Массачусетс: Belknap Press, 2003, стр. 415 . Кроме того, что касается заметок Ф. вплоть до D ♭ , в Энциклопедии микротональной музыки Tonalsoft говорится: «Фактически эта структура прекрасно описывает . просто-интонационную структуру Салинаса»
^ Самое старое известное описание пифагорейской системы настройки встречается в вавилонских артефактах. См.: Уэст, М.Л. «Вавилонская нотная запись и хурритские мелодические тексты», Music & Letters , vol. 75, нет. 2 (май 1994 г.). стр. 161–179.

Внешние ссылки

Искусство Штатов: микротональные/справедливые интонационные произведения с использованием справедливой интонации американских композиторов
The Chrysalis Foundation – Просто интонация: два определения
Гитара 21 Tone Just Intonation Данте Розати
«Просто интонация», Марк Новицки
Просто интонация, объясненная Кайл Ганн
Подборка работ Just Intonation, отредактированных сетью Just Intonation Network, опубликованных в архиве проекта журнала Tellus Audio Cassette Magazine на UbuWeb.
Фонд средневековой музыки и искусства
Music Novatory - Just Intonation. Архивировано 15 июня 2011 г. в Wayback Machine.
Почему Just Intonation звучит так хорошо?
Архивы Уилсона
Барбьери, Патрицио. Энгармонические инструменты и музыка, 1470–1900 гг . (2008) Латина, Иль Леванте
Программное обеспечение для клавиатуры 22 Note Just Intonation с 12 звуками индийских инструментов Libreria Editrice
Plainsound Music Edition - Музыка и исследования с простой интонацией (JI), информация о Гельмгольца - Эллиса JI. нотации

[1] Райт, Дэвид (2009). Математика и музыка , стр. 140–141. ISBN 978-0-8218-4873-9 .

[2] Джонстон, Бен и Гилмор, Боб (2006). «Система обозначений для расширенной простой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , с. 78. ISBN 978-0-252-03098-7 .

[Fonville-3] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот Джон Фонвилл . «Расширенная справедливая интонация Бена Джонстона - Руководство для переводчиков», стр. 113–114, « Перспективы новой музыки» , том. 29, нет. 2 (лето 1991 г.), стр. 106–137.

[4] Примечания от G ♯ до D ♭ взяты из Дона Майкла Рэндела , Гарвардский музыкальный словарь , 4-е издание. Кембридж, Массачусетс: Belknap Press, 2003, стр. 415 . Кроме того, что касается заметок Ф. вплоть до D ♭ , в Энциклопедии микротональной музыки Tonalsoft говорится: «Фактически эта структура прекрасно описывает . просто-интонационную структуру Салинаса»

[5] Самое старое известное описание пифагорейской системы настройки встречается в вавилонских артефактах. См.: Уэст, М.Л. «Вавилонская нотная запись и хурритские мелодические тексты», Music & Letters , vol. 75, нет. 2 (май 1994 г.). стр. 161–179.

[1]

[2]

[3]

[4]

[5]

v т и инструмента Интонация
Просто интонация в любой тональности	Безладовый струнный инструмент Педальная стальная гитара Тромбон Литавры Человеческий голос Синтезатор
Динамическая регулировка интонации	Крук Ладовый струнный инструмент Духовые инструменты
Просто интонация в одной тональности	Волынки Натуральный рог Смерч Длиннострунный инструмент Гармоника
Возвратный к простому ключу	Клавишные инструменты Сплит острый
Тоны флажоле (гармоники) или натуральных обертонов серия	Гуцинь Дэн Бау
Физическая только что произнесенная строка часть связи с дополнительным третьим мостом	монохорд Пенчилина Мудсвингер