Гексани

7-ступенчатая шестигранная шкала

9- предельная шкала гексани без 7

Проблемы с воспроизведением этих файлов? См. справку для СМИ .

В музыкальных системах настройки гексани , изобретенный Эрвом Уилсоном , ^[1] представляет собой одну из простейших структур, встречающихся в его наборах комбинированных продуктов .

Ее называют нецентрированной структурой, что означает отсутствие тоника. Это достигается за счет использования консонантных отношений в отличие от методов диссонанса, обычно используемых в атональности. Хотя его часто и досадно перекрывают с родом Эйлера-Фоккера , последующая звездность наборов комбинированных продуктов (CPS) Уилсона находится за пределами этого рода. Род Эйлера-Фоккера не рассматривает 1 как возможный член множества, за исключением отправной точки. Числа вершин его комбинационных множеств соответствуют числам в треугольнике Паскаля . В этой конструкции гексани является третьим сечением четырехфакторного множества и первым нецентрированным. гексани — это название, которое Эрв Уилсон дал шести нотам в наборе комбинированных продуктов 2 из 4, сокращенно 2*4 CPS. ^[2]

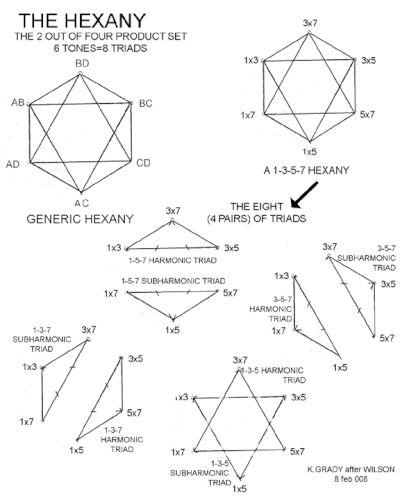
Проще говоря, гексани — это набор 2 из 4. Он строится путем взятия любых четырех факторов и набора из двух одновременно, а затем их попарного умножения. Например, гармонические факторы 1, 3, 5 и 7 объединяются в пары 1*3, 1*5, 1*7, 3*5, 3*7, 5*7, в результате чего получаются 1, 3, 5, 7 гексаний. Ноты обычно сдвинуты на октаву, чтобы разместить их все в одной октаве, что не влияет на интервальные отношения и созвучие трезвучий. Возможность того, что октава станет решением, не выходит за рамки концепции Уилсона и используется в случаях размещения более крупных комбинированных наборов продуктов на универсальных клавиатурах.

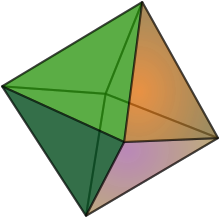
Гексани можно рассматривать как аналог октаэдра . Ноты расположены так, что каждая точка представляет высоту звука, каждый край — интервал, а каждая грань — трезвучие. Таким образом, он имеет восемь интонационных трезвучий, каждое из которых имеет две общие ноты с тремя другими аккордами. Каждое трезвучие встречается только один раз, его инверсия представлена тремя противоположными тонами. На краях октаэдра показаны музыкальные интервалы между вершинами, обычно выбираемые в качестве согласных интервалов из гармонического ряда. Точки представляют собой музыкальные ноты, а три ноты, образующие каждую из треугольных граней, представляют собой музыкальные трезвучия. Уилсон также указал и исследовал идею мелодичных гексаний.

Тюнинг

Это показывает трехмерную версию гексани.

Орфографическая проекция.

Dekany 1 3 5 7 9

9-ти предельная деканская шкала

Проблемы с воспроизведением этого файла? См. справку для СМИ .

Гексани — это фигура, содержащая как показанные треугольники, так и соединительные линии между ними.

В этой 2D-конструкции интервальные соотношения такие же. См. также рисунок 2 статьи Крейга Грейди. ^[3]

Например, грань с вершинами 3×5, 1×5, 5×7 является аккордом отона (мажорного типа), поскольку ее можно записать как 5×(1, 3, 7), используя гармоники с низкими номерами . 5×7, 3×7, 3×5 — это утональный аккорд (минорный тип), поскольку его можно записать как 3×5×7×(1/3, 1/5, 1/7), используя малонумерованные аккорды. субгармоники .

Чтобы превратить это в традиционную гармоническую конструкцию с 1/1 в качестве первой ноты, все ноты сначала уменьшаются до октавы. Поскольку гармоническая конструкция, как ее назвал Эрв, поскольку он не считал ее гаммой и у нее еще нет 1/1, любая выбранная нота может использоваться для разделения каждой ноты с точностью до октавного уменьшения. Обозначения соотношений здесь показывают соотношения частот нот. Если 1/1 — это 500 герц, то 6/5 — 600 герц и так далее.

В музыке

Композиторы, в том числе Крейг Грейди , Дэниел Джеймс Вольф и Джозеф Персон, использовали структуру высоты звука, основанную на гексани. ^{[ нужна ссылка ]}

См. также

Род Эйлера-Фоккера

Ссылки

^ Чалмерс, Джон Х. (1993). Деления тетрахорда: пролегомен к построению музыкальных гамм , стр.116. Музыка Лягушачьего Пика. ISBN 978-0-945996-04-0 .
^ ^{[ автор отсутствует ]} (1993). Музыкальные произведения, выпуски 55–60 , стр.43. Музыкальная галерея.
^ Грейди, Крейг (1991). «Гексани Эрвина Уилсона» (PDF) . Просто интонация . 7 (1): 8–11.

Дальнейшее чтение

Нарушима, Теруми (2018). Микротональность и системы настройки Эрва Вильсона . Лондон. ISBN 978-1-315-71858-3 . OCLC 1019658301 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
Грейди, Крейг (1991), «Гексания Эрвина Уилсона» (PDF) , Just Intonation , vol. 7, нет. 1, стр. 8–11.
Шимер, Грег, «Темперированный Деканис: эффект хора с использованием микротональных интервалов, основанный только на интонации» (PDF) , Материалы 7-й Международной конференции по восприятию и познанию музыки, Сидней, 2002 , стр. 300–302 ^{[ мертвая ссылка ]} (см. раздел «Справочная информация»)
Уилсон, Эрв. «Д'Алессандро, как ураган» (PDF) . Ксенгармоникон . 12:10 , 21.

Внешние ссылки

«Немного гексани и алмазных решеток (и заготовок) из гексани» , Архив Уилсона . Оригинальные бумаги из гексанита, показывающие различные грани и конфигурации, собранные не Эрвом Уилсоном (с 1967 г.)
«Архивы Уилсона» , Anaphoria.com
«гексани» , RobertInventor.com . С помощью гексани вы можете развернуться и щелкнуть по любой его вершине, ребру или грани, чтобы услышать аккорды.
«Шаблоны наборов комбинированных продуктов» , Xenharmonicon IX (1986), Крейг Грейди.
«Документы Эйкосани» , Anaphoria.com .
«Музыкальная геометрия» , Музыка и виртуальные цветы . Введение. к музыкальной геометрии.
«The Tumbling Dekany» , «Необычные музыкальные гаммы», домашняя страница Дэйва Кинана . «Декани» Дэйва Кинана, кувыркающийся в 4 измерениях — как музыкальная таблица Excel

[1] Чалмерс, Джон Х. (1993). Деления тетрахорда: пролегомен к построению музыкальных гамм , стр.116. Музыка Лягушачьего Пика. ISBN 978-0-945996-04-0 .

[2] {[ автор отсутствует ]} (1993). Музыкальные произведения, выпуски 55–60 , стр.43. Музыкальная галерея.

[3] Грейди, Крейг (1991). «Гексани Эрвина Уилсона» (PDF) . Просто интонация . 7 (1): 8–11.

[1]

[2]

[3]