Цент (музыка)

Один цент по сравнению с полутоном усеченного монохорда .

Октавы увеличиваются экспоненциально при измерении по линейной шкале частот (Гц).

Октавы расположены на одинаковом расстоянии друг от друга при измерении в логарифмическом масштабе (центах).

Цент логарифмическая — музыкальных единица измерения интервалов . Двенадцатитоновая равнотемперация делит октаву на 12 полутонов по 100 центов каждый. Обычно центы используются для выражения небольших интервалов, для проверки интонации или для сравнения размеров сопоставимых интервалов в разных системах настройки . Для людей один цент слишком мал, чтобы его можно было воспринимать между последовательными нотами.

Центы, как их описал Александр Джон Эллис , следуют традиции измерения интервалов с помощью логарифмов , которая началась с Хуана Карамуэля-и-Лобковица в 17 веке. Эллис решил основывать свои измерения на сотой доле полутона. ¹²⁰⁰ √ 2 , по Роберта Холфорда Макдауэлла Бозанкета предложению . Проведя обширные измерения музыкальных инструментов со всего мира, Эллис использовал центы, чтобы составить отчет и сравнить используемые шкалы. и далее описал и использовал эту систему в своем издании 1875 года « Германа фон Гельмгольца » О ощущениях тона . Это стало стандартным методом представления и сравнения музыкальных тонов и интервалов.

История

Александра Джона Эллиса Статья «О музыкальных гаммах разных народов» , опубликованный Журналом Общества искусств в 1885 году, официально представил систему центов, которая будет использоваться при изучении путем сравнения и сопоставления музыкальных гамм различных народов. Система центов уже была определена в его «Истории музыкальной высоты звука» , где Эллис пишет: «Если бы мы предположили, что между каждой парой соседних нот, образующих равный полутон [...], было бы вставлено 99 других нот, образующих точно равные интервалами друг с другом, мы должны разделить октаву на 1200 равных сотен [ sic ] одинакового полутона, или центов , как их можно кратко назвать».

Эллис определил высоту музыкальной ноты в своей работе 1880 года « История музыкальной высоты звука». это «количество двойных или полных колебаний вперед и назад, совершаемых за каждую секунду частицей воздуха, пока слышна нота». Позже он определил музыкальную высоту как «высоту звука или V [для «двойных вибраций»] любой названной музыкальной ноты, которая определяет высоту всех остальных нот в определенной системе настроек». Он отмечает, что эти ноты, когда они звучат последовательно, образуют гамму инструмента, а интервал между любыми двумя нотами измеряется «отношением меньшего номера тона к большему или дробью, образованной путем деления большего на тем меньше». абсолютный и относительный шаг . На основе этих соотношений также определялись

Эллис отметил, что «цель тюнера состоит в том, чтобы сделать интервал [...] между любыми двумя нотами, отвечающими на любые две соседние клавиши пальца по всему инструменту, абсолютно одинаковым. Результат называется равной темперацией или настройкой, и является ли система в настоящее время используется по всей Европе. Далее он приводит расчеты, позволяющие приблизительно оценить соотношение в центах, добавляя, что «как правило, нет необходимости выходить за пределы ближайшего целого числа центов».

В этой статье Эллис представляет применение системы центов в музыкальных гаммах различных народов, в том числе: (I. Гептатонические гаммы) Древняя Греция и Современная Европа, Персия, Аравия, Сирия и Шотландское нагорье, Индия, Сингапур, Бирма и Сиам; (II. Пентатоника) Южная часть Тихого океана, Западная Африка, Ява, Китай и Япония. И он приходит к выводу, что «Музыкальная гамма не едина, не «естественна» и даже не основана обязательно на законах строения музыкального звука, так прекрасно разработанных Гельмгольцем, а очень разнообразна, очень искусственна и очень капризна. ".

Использовать

Сравнение равнотемперированных (черный) и пифагорейских (зеленый) интервалов, показывающее связь между соотношением частот и значениями интервалов в центах.

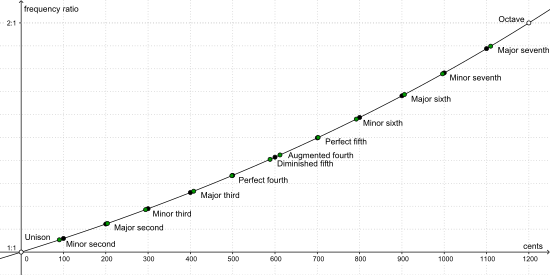
Цент — единица измерения отношения двух частот. полутон Равномерный (интервал между двумя соседними клавишами фортепиано) по определению составляет 100 центов. Октава — две ноты с соотношением частот 2:1 — охватывает двенадцать полутонов и, следовательно, 1200 центов. Отношение частот с разницей в один цент в точности равно 2 ^{1 ⁄ 1200} = ¹²⁰⁰ √ 2 , корень 1200-й степени из 2, что примерно равно 1.000 577 7895 . Таким образом, повышение частоты на один цент соответствует умножению исходной частоты на это постоянное значение. Увеличение частоты на 1200 центов удваивает частоту, в результате чего получается ее октава.

Если знать частоты $f_{1}$ и $f_{2}$ из двух банкнот, количество центов $c$ измеряя интервал от $f_{1}$ к $f_{2}$ является:

$c=1200\cdot \log _{2}\left({\frac {f_{2}}{f_{1}}}\right)$

Аналогично, если знать $f_{1}$ и количество центов $c$ в интервале от $f_{1}$ к $f_{2}$, затем $f_{2}$ равно:

$f_{2}=f_{1}\times 2^{\frac {c}{1200}}\,.$

Сравнение мажорной терции в справедливом и равном темпераменте

Большая терция в чистой интонации имеет соотношение частот 5:4 или ~386 центов, а в равнотемперированной - 400 центов. Эта разница в 14 центов составляет примерно седьмую полшага и достаточно велика, чтобы ее можно было услышать.

Кусочно-линейная аппроксимация

По мере увеличения x от 0 до 1 ⁄ 12 , функция 2 ^х увеличивается почти линейно от 1,000 00 до 1,059 46 , что позволяет использовать кусочно-линейную аппроксимацию . Таким образом, хотя центы представляют собой логарифмическую шкалу, небольшие интервалы (менее 100 центов) можно приблизительно аппроксимировать линейным соотношением 1 + 0,000 5946.  $c$ вместо истинного показательного соотношения 2 ^{c ⁄ 1200} . Ошибка округления равна нулю, если $c$ равно 0 или 100 и составляет всего около 0,72 цента при $c$= 50 (чье правильное значение 2 ^{1 ⁄ 24} ≅ 1,029 30 аппроксимируется 1 + 0,000 5946 × 50 ≅ 1,02973). Эта погрешность значительно ниже всего, что может услышать человек, что делает эту кусочно-линейную аппроксимацию адекватной для большинства практических целей.

Человеческое восприятие

Формы сигналов унисона (синий) и цента (красный) практически неотличимы.

Трудно установить, сколько центов воспринимается человеком; эта точность сильно варьируется от человека к человеку. Один автор заявил, что люди могут различать разницу в высоте звука примерно в 5–6 центов. Порог чувствительности, технически известный как едва заметная разница (JND), также варьируется в зависимости от частоты, амплитуды и тембра . В одном исследовании изменения качества звука снизили способность студентов-музыкантов распознавать расстроенные высоты звука, которые отклонялись от соответствующих значений на ± 12 центов. Также было установлено, что усиление тонального контекста позволяет слушателям более точно судить о высоте звука. «Хотя интервалы менее нескольких центов незаметны для человеческого уха в мелодическом контексте, в гармонии очень небольшие изменения могут вызвать большие изменения в долях и шероховатости аккордов».

Есть свидетельства того, что при прослушивании высоты звука с вибрато люди воспринимают среднюю частоту как центр высоты звука. Одно исследование современного исполнения « Аве Марии» Шуберта показало, что диапазон вибрато обычно находится в диапазоне от ± 34 центов до ± 123 центов со средним значением ± 71 цент, и отметило более высокие вариации в оперных ариях Верди .

Нормальные взрослые способны очень надежно распознавать разницу в высоте звука всего в 25 центов. Однако взрослым с амузией трудно распознавать различия менее 100 центов, а иногда возникают проблемы с этими или более крупными интервалами.

Другие представления интервалов логарифмами

Октава

Представление музыкальных интервалов логарифмами почти так же старо, как и сами логарифмы. Логарифмы были изобретены лордом Нейпиром в 1614 году. Еще в 1647 году Хуан Карамуэль-и-Лобковиц (1606-1682) в письме Афанасию Кирхеру описал использование логарифмов с основанием 2 в музыке. В этой базе октава обозначается 1, полутон — 1/12 и т. д.

Гептамериды

Жозеф Совер в своей книге «Принципы акустики и музыки» 1701 года предложил использовать логарифмы с основанием 10, вероятно, потому, что были доступны таблицы. Он использовал логарифмы, вычисляемые с тремя десятичными знаками. Логарифм 2 по основанию 10 равен примерно 0,301, который Совер умножает на 1000, чтобы получить 301 единицу в октаве. Чтобы работать с более управляемыми единицами, он предлагает взять 7/301, чтобы получить единицы 1/43 октавы. Таким образом, октава разделена на 43 части, называемые «меридами», которые сами разделены на 7 частей, «гептамериды». Совер также предполагал возможность дальнейшего разделения каждого гептамерида на 10, но на самом деле не использовал такие микроскопические единицы.

Савар

Феликс Савар (1791–1841) перенял систему Совера, не ограничивая количество десятичных знаков логарифма 2, так что значение его единицы варьируется в зависимости от источников. С пятью десятичными знаками десятичный логарифм числа 2 равен 0,30103, что дает 301,03 саварта в октаве. Это значение часто округляется до 1/301 или до 1/300 октавы.

Прони

В начале XIX века Гаспар де Прони предложил логарифмическую единицу измерения. ${\sqrt[{12}]{2}}$, где единица соответствует полутону равной темперации. Александр Джон Эллис в 1880 году описывает большое количество стандартов высоты звука, которые он отметил или рассчитал, указывая в прони с двумя десятичными знаками, то есть с точностью до 1/100 полутона. интервал, отделявший их от теоретической высоты 370 Гц, взятой за точку отсчета.

Сантитоны

Сантитон музыкальным (также Иринг ) также является интервалом (2 ^{1 ⁄ 600} , ${\sqrt[{600}]{2}}$), равный двум центам (2 ^{2 ⁄ 1200} ) предложена в качестве единицы измерения ( ) Видогаста Иринга в «Die reine Stimmung in der Musik» (1898) как 600 шагов на октаву , а затем Джозефа Яссера в «Теории эволюции тональности» (1932) как 100 шагов на один равномерный целый тон .

Иринг заметил, что Град/Веркмейстер (1,96 цента, 12 на пифагорейскую запятую ) и раскол (1,95 цента) почти одинаковы (≈ 614 шагов на октаву), и оба могут быть аппроксимированы 600 шагами на октаву (2 цента). Яссер продвигал децитон , сантитон и миллитон (10, 100 и 1000 шагов на целый тон = 60, 600 и 6000 шагов на октаву = 20, 2 и 0,2 цента).

Например: равная темперированная чистая пятая = 700 центов = 175,6 саваров = 583,3 миллиоктавы = 350 сентитонов.

Сантитоны	центы
1 сантитон	2 цента
0,5 сантитона	1 цент
2 1 ⁄ 600	2 2 ⁄ 1200
50 за полутон	100 на полутон
100 за целый тон	200 за целый тон

Звуковые файлы

Следующие аудиофайлы воспроизводятся с различными интервалами. В каждом случае первой сыгранной нотой является средняя нота «до». Следующая нота выше «до» на присвоенное значение в центах. Наконец, две ноты играются одновременно.

Обратите внимание, что JND для разницы высоты звука составляет 5–6 центов. При исполнении по отдельности ноты могут не проявлять заметной разницы, но при их совместном исполнении могут быть слышны биения (например, если звучат средняя до и нота на 10 центов выше). В любой конкретный момент две формы сигналов в большей или меньшей степени усиливают или нейтрализуют друг друга, в зависимости от их мгновенного фазового соотношения. Настройщик фортепиано может проверить точность настройки, определяя время ударов при одновременном звучании двух струн.

, частота биений = 0,16 Гц
, частота биений = 1,53 Гц
, частота биений = 3,81 Гц

См. также

• Степень
• Градиан
• Микротональная музыка
• Радиан

Ссылки

Источники

• Апель, Вилли (1970). Гарвардский музыкальный словарь . Тейлор и Фрэнсис.
• Барбьери, Патрисия (1987). «Хуан Карамуэль Лобковиц (1606–1682): о музыкальных логарифмах и проблеме музыкальной температуры». Теория музыки . 2 (2): 145–168.
• Бенсон, Дэйв (2007). Музыка: математическое предложение . Кембридж. ISBN  9780521853873 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Браун, Дж. К.; Вон, КВ (сентябрь 1996 г.). «Центр высоты звука вибрато струнных инструментов» (PDF) . Журнал Акустического общества Америки . 100 (3): 1728–1735. Бибкод : 1996ASAJ..100.1728B . дои : 10.1121/1.416070 . ПМИД   8817899 . Проверено 28 сентября 2008 г.
• Эллис, Александр Дж .; Хипкинс, Альфред Дж. (1884), «Тонометрические наблюдения над некоторыми существующими негармоничными музыкальными гаммами», Proceedings of the Royal Society of London , 37 (232–234): 368–385, doi : 10.1098/rspl.1884.0041 , JSTOR   114325 , Зенодо : 1432077 .
• Эллис, Александр Дж. (1880), «История музыкальной высоты» , Журнал Общества искусств , 21 (545): 293–337, Бибкод : 1880Natur..21..550E , doi : 10.1038/021550a0 , S2CID   4107831
• Эллис, Александр Дж. (1885), «О музыкальных масштабах разных народов» , Журнал Общества искусств : 485–527 , получено 1 января 2020 г.
• Фарнсворт, Пол Рэндольф (1969). Социальная психология музыки . Издательство Университета штата Айова. ISBN  9780813815473 .
• Герингер, Дж. М.; Уорти, доктор медицины (1999). «Влияние изменений качества тона на интонацию и рейтинги качества тона инструменталистов средней школы и колледжа». Журнал исследований в области музыкального образования . 47 (2): 135–149. дои : 10.2307/3345719 . JSTOR   3345719 . S2CID   144918272 .
• Леффлер, Д.Б. (апрель 2006 г.). Тембры инструментов и оценка высоты звука в полифонической музыке (магистратура). Кафедра электротехники и вычислительной техники Технологического института Джорджии. Архивировано из оригинала 18 декабря 2007 г.
• Перец, И.; Хайд, КЛ (август 2003 г.). «Что особенного в обработке музыки? Выводы из врожденной амузии». Тенденции в когнитивных науках . 7 (8): 362–367. CiteSeerX   10.1.1.585.2171 . дои : 10.1016/S1364-6613(03)00150-5 . ПМИД   12907232 . S2CID   3224978 .
• Праме, Э. (июль 1997 г.). «Степень вибрато и интонация в профессиональном западном лирическом пении» . Журнал Акустического общества Америки . 102 (1): 616–621. Бибкод : 1997ASAJ..102..616P . дои : 10.1121/1.419735 .
• Рэндел, Дон Майкл (1999). Гарвардский краткий словарь музыки и музыкантов . Издательство Гарвардского университета. ISBN  978-0-674-00084-1 .
• Рэндел, Дон Майкл (2003). Гарвардский музыкальный словарь (4-е изд.). Издательство Гарвардского университета. ISBN  978-0-674-01163-2 .
• Ренольд, Мария (2004) [1998], Анна Мейсс (редактор), Интервалы, гаммы, тона и концертная высота C = 128 Гц , перевод Бевиса Стивенса, Temple Lodge, ISBN  9781902636467 , Пропорции интервалов можно преобразовать в значения центов, которые широко используются сегодня. {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Уорриер, CM; Заторре, Р.Дж. (февраль 2002 г.). «Влияние тонального контекста и тембральных вариаций на восприятие высоты звука» . Восприятие и психофизика . 64 (2): 198–207. дои : 10.3758/BF03195786 . ПМИД   12013375 . S2CID   15094971 .
• Ясир, Джозеф (1932). Теория эволюции тональности . Американская библиотека музыковедения.

Внешние ссылки

• Преобразование центов: соотношение целых чисел к центам. Архивировано 22 апреля 2017 г. в Wayback Machine [округлено до целого числа].
• Конвертация центов: онлайн-утилита с несколькими функциями