Запятая (музыка)

В теории музыки запятая — это очень маленький интервал , разница возникает в результате настройки одной ноты двумя разными способами. ^[1] Строго говоря, существует только два вида запятых: синтонная запятая , «разница между просто мажорной терцией и четырьмя просто идеальными квинтами за вычетом двух октав», и пифагорейская запятая , «разница между двенадцатью квинтами и семью октавами». ^[2] Слово запятая, используемое без уточнений, относится к синтонной запятой , ^[3] например, как разницу между F ♯, на основе D настроенным с использованием пифагорейской системы настройки , и другим F ♯, на основе D. среднего тона с четвертью запятой настроенным с использованием системы настройки который можно определить , Интервалы, разделенные соотношением 81:80, считаются одной и той же нотой, поскольку 12-нотная западная хроматическая шкала не отличает пифагорейские интервалы от 5-предельных интервалов в своих обозначениях. Другие интервалы считаются запятыми из-за энгармонической эквивалентности системы настройки. Например, в 53TET , B ♭ и A ♯ аппроксимируются одним и тем же интервалом, хотя они находятся на семеричной клеизме друг от друга.

Этимология

В данном контексте «запятая» означает «волосик», то есть «отрезать всего лишь волосок». ^{[ нужна ссылка ]}. Слово «запятая» пришло из латыни от греческого $κόμμα$ , от более раннего * $κοπ-μα$ : «результат или эффект разрезания». Более полная этимология приведена в статье $κόμμα$ (Древнегреческий) в Викисловаре .

Описание

В пределах одной и той же системы настройки две энгармонически эквивалентные ноты (например, G ♯ и A ♭ ) могут иметь немного разную частоту, а интервал между ними представляет собой запятую. Например, в расширенных гаммах, созданных с настройкой с пятью пределами, нота A ♭ , настроенная как мажорная треть ниже C ₅ , и G ♯, настроенная как две мажорные трети выше C _4, не являются совершенно одной и той же нотой, поскольку они были бы в равной темперации . Интервал между этими нотами, диезиса , представляет собой легко слышимую запятую (ее размер составляет более 40% полутона ) .

Запятые часто определяют как разницу в размере двух полутонов. ^{[ нужна ссылка ]} Каждая темперамента система настройки означает 12 тонов, характеризующихся двумя разными типами полутонов (диатоническими и хроматическими) и, следовательно, запятой уникального размера. То же самое справедливо и для пифагорейской настройки.

В одной только интонации может быть получено более двух видов полутонов. Таким образом, одна система настройки может характеризоваться несколькими разными запятыми. Например, широко используемая версия пятипредельной настройки дает 12-тоновую гамму с четырьмя видами полутонов и четырьмя запятыми .

Размер запятых обычно выражается и сравнивается в центах : 1/1200 октавы доли . в логарифмическом масштабе

Запятые в разных контекстах

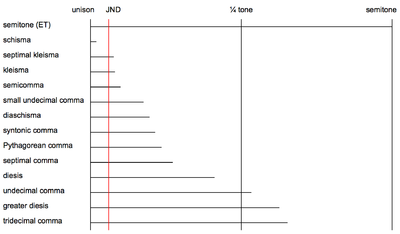
В столбце ниже «Разница между полутонами » мин 2 — это минорная секунда (диатонический полутон), ^август1 — это расширенный унисон (хроматический полутон), а S ₁ , S ₂ , S ₃ , S ₄ — это полутона, определенные здесь . В столбцах с надписью « Интервал 1» и «Интервал 2» предполагается, что все интервалы настроены только по интонации . Обратите внимание, что запятая Пифагора ( $κ$ _𝜋 ) и синтонная запятая ( $κ$ _S ) являются основными интервалами, которые можно использовать в качестве критериев для определения некоторых других запятых. Например, разница между ними — маленькая запятая, называемая схизма . Раскол не слышен во многих контекстах, поскольку его размер уже, чем наименьшая слышимая разница между тонами (которая составляет около шести центов, также известная как едва заметная разница , или JND).

Название запятой	Альтернативное название	Определения				Размер
		Разница между полутона	Разница между запятые	Разница между		центы	Соотношение
		Разница между полутона	Разница между запятые	Интервал 1	Интервал 2	центы	Соотношение
раскол	skhisma	^август1 - мин 2 в ⁠ 1/12 один ⁠ запятая означает	1 $к$ _𝜋 − 1 $к$ _S	8 идеальных пятых + 1 большая треть	5 октав	1.95	${\tfrac {\ 32805\ }{32768}}$
семеричная клейсма				3 основные трети	1 октава — 1 семеричная запятая	7.71	${\tfrac {\ 225\ }{224}}$
клейсма				6 малых третей	1 октава + 1 идеальная пятая часть (« тритаве »)	8.11	${\tfrac {\ 15625\ }{15552}}$
маленькая недесятичная запятая ^[4]				1 нейтральная секунда	1 минорный тон	17.40	${\tfrac {\ 100\ }{99}}$
диашизм	диашизм	мин 2 - ^август1 в ⁠ 1/6 запятую ⁠ означало , С3 − _С2 в 5-лимитном тюнинге	2 $k$ _S − 1 $k$ _𝜋	3 октавы	4 идеальных квинты + 2 основные трети	19.55	${\tfrac {\ 2048\ }{2025}}$
синтонная запятая ( $κ$ _С )	У нас есть две запятые	С ₂ - С ₁ в 5-лимитном тюнинге		4 идеальных пятых	2 октавы + 1 большая треть	21.51	${\tfrac {\ 81\ }{80}}$
синтонная запятая ( $κ$ _С )	У нас есть две запятые	С ₂ - С ₁ в 5-лимитном тюнинге		мажорный тон	минорный тон	21.51	${\tfrac {\ 81\ }{80}}$
53 ТЕТ запятая ( $к$ ₅₃ )	1 шаг (в 53 ТЕТ )	⁠ 1/9 ⁠ мажорный тон (в 53 ТЕТ )	⁠ 1/8 ⁠ минорный тон (в 53 ТЕТ )	мажорный тон (в 53 ТЕТ )	минорный тон (в 53 ТЕТ )	22.64	${\bigl (}2{\bigr )}^{\tfrac {\ 1\ }{53}}$
Пифагорова запятая ( $к$ _𝜋 )	дитоническая запятая	^август1 - мин 2 (в пифагорейской настройке )		12 идеальных пятых	7 октав	23.46	${\tfrac {\ 531441\ }{524288}}$
семеричная запятая ^[5]	Запятая Архита ( $к$ _А )			малая седьмая	септимальная минорная седьмая	27.26	${\tfrac {\ 64\ }{63}}$
острый	менее острый уменьшенная секунда	мин 2 - ^август1 в ⁠ 1/4 ⁠ запятая означала , С ₃ - С ₁ в 5-лимитном тюнинге	3 $κ$ _S − 1 $κ$ _𝜋	октава	3 основные трети	41.06	${\tfrac {\ 128\ }{125}}$
недесятичная запятая ^[5]^[6]	Недесятичный четверть тона			одиннадцатый тритон	идеальная четвертая	53.27	${\tfrac {\ 33\ }{32}}$
больший диезис		мин 2 - ^август1 в ⁠ 1/3 запятую ⁠ означало , С ₄ - С ₁ в 5-лимитном тюнинге	4 $k$ _S − 1 $k$ _𝜋	4 второстепенные трети	октава	62.57	${\tfrac {\ 648\ }{625}}$
трехдесятичная запятая	трехзначный третий тон			трехдесятичный тритон	идеальная четвертая	65.34	${\tfrac {\ 27\ }{26}}$

Многие другие запятые были перечислены и названы микротоналистами. ^[7]

Синтоническая запятая сыграла решающую роль в истории музыки. Это степень, на которую некоторые ноты, полученные при пифагорейской настройке, были сглажены или обострены, чтобы образовались только второстепенные и мажорные трети. В пифагорейской настройке единственными очень согласными интервалами были чистая квинта и ее инверсия, идеальная кварта . Пифагорейская мажорная терция (81:64) и минорная терция (32:27) были диссонансными , и это мешало музыкантам свободно использовать трезвучия и аккорды , заставляя их писать музыку с относительно простой фактурой . Музыканты позднего средневековья признавали, что, слегка смягчая высоту некоторых нот, пифагорейские терции можно сделать созвучными . Например, если вы уменьшите частоту E на синтонную запятую (81:80), C–E (большая терция) и E–G (малая терция) станут справедливыми: C–E сглаживается справедливым соотношением

{\frac {\ 81\ }{64}}\cdot {\frac {\ 80\ }{81}}={\frac {\ 1\cdot 5\ }{4\cdot 1}}={\frac {\ 5\ }{4}}

и в то же время E–G заточена до точного соотношения

{\frac {32}{\ 27\ }}\cdot {\frac {81}{\ 80\ }}={\frac {2\cdot 3}{\ 1\cdot 5\ }}={\frac {6}{\ 5\ }}

Это привело к созданию новой системы настройки , известной как четверть запятой , которая позволяла полноценно развивать музыку со сложной текстурой , например полифоническую музыку или мелодии с инструментальным сопровождением . С тех пор были разработаны другие системы настройки, и синтонная запятая использовалась в качестве эталонного значения для смягчения идеальных квинт во всем семействе синтонических темпераментов , включая средние темпераменты .

Альтернативные определения

В четверти запятой означает уменьшенную секунду и любую систему настройки темперамента, которая смягчает квинту до размера меньше 700 центов, запятая представляет собой уменьшенную секунду , которую можно эквивалентно определить как разницу между:

минорная секунда и расширенный унисон (также известный как диатонические и хроматические полутона ) или
большая секунда и уменьшенная треть , или
малая треть и увеличенная секунда , или
большая треть и уменьшенная кварта , или
идеальная кварта и увеличенная треть , или
увеличенная кварта и уменьшенная квинта , или
идеальная квинта и уменьшенная шестая , или
малая шестая и увеличенная пятая , или
большая шестая и уменьшенная седьмая , или
минорная седьмая и увеличенная шестая , или
мажорная седьмая и уменьшенная октава .

В пифагорейской настройке и любой системе настройки среднего темперирования, которая смягчает квинту до размера, превышающего 700 центов (например, ⁠ 1/12 противоположностью уменьшенной секунды, а значит , означала), запятая является ⁠ запятая противоположностью вышеперечисленных различий. Точнее, в этих системах настройки уменьшенная секунда представляет собой нисходящий интервал, а запятая — его восходящую противоположность. Например, пифагорейская запятая (531441:524288, или около 23,5 центов) может быть вычислена как разница между хроматическим и диатоническим полутоном, что является противоположностью уменьшенной пифагорейской секунды (524288:531441, или около -23,5 цента). .

В каждой из вышеперечисленных систем тюнинга вышеперечисленные различия имеют одинаковый размер. Например, в пифагорейской настройке все они равны противоположности пифагорейской запятой , а в четвертной запятой, означающей один, все они равны диезису .

Обозначения

В 2000–2004 годах Марк Сабат и Вольфганг фон Швайниц вместе работали в Берлине над разработкой метода точного указания высоты звука в нотной записи. Этот метод получил название расширенной нотации высоты тона Гельмгольца-Эллиса JI . ^[8] Сабат и Швайниц рассматривают «обычные» бемоли, натуральные и диезы как пифагорейскую серию идеальных квинт. Таким образом, серия идеальных квинт, начинающаяся с F, продолжается CGDAEBF ♯ и так далее. Преимущество для музыкантов состоит в том, что традиционное прочтение основных четвертей и квинт остается привычным. Такой подход также отстаивали Дэниел Джеймс Вольф и Джо Монзо, который называет его аббревиатурой HEWM (Гельмгольц-Эллис-Вольф-Монцо). ^[9] В дизайне Сабата-Швайница синтонические запятые обозначаются стрелками, прикрепленными к плоскому, естественному или острому знаку, семеричные запятые - с использованием символа Джузеппе Тартини, а недесятичные четвертьтона - с использованием общепринятых четвертьтоновых знаков (одиночный крест и обратная плоскость ). Для высших простых чисел разработаны дополнительные знаки. Чтобы облегчить быструю оценку высоты тона, можно добавить указание в центах (отклонения вниз ниже и отклонения вверх выше соответствующего случайного значения). Используемое соглашение заключается в том, что написанные центы относятся к темперированной высоте звука, подразумеваемой плоским, естественным или диезным знаком и названием ноты. Одним из больших преимуществ любой такой записи является то, что она позволяет точно записать естественный гармонический ряд. Полная легенда и шрифты для обозначений (см. примеры) находятся в открытом исходном коде и доступны в Plainsound Music Edition. ^{[ нужна полная цитата ]} Таким образом, шкала Пифагора — это CDEFGABC , а правильная шкала — CDE. ФГА Б С.

Композитор Бен Джонстон использует знак «-», чтобы указать, что нота опускается на синтоническую запятую, или «+», чтобы указать, что нота поднимается на синтоническую запятую; ^[10] однако «базовая гамма» Джонстона (простые номиналы ABCDEFG ) настроена на чистую интонацию и, таким образом, уже включает синтонную запятую. Таким образом, пифагорейская шкала — это CD E+ FG A+ B+ C , а правильная — CDEFGAB .

Умеренность запятых

Запятые часто используются при описании музыкальных темпераментов , где они описывают различия между музыкальными интервалами, которые устраняются этой системой настройки. Запятую можно рассматривать как расстояние между двумя музыкальными интервалами. Когда в системе настройки заданная запятая смягчается, возможность различать эти два интервала в этой настройке теряется. Например, разница между диатоническим полутоном и хроматическим полутоном называется диезисом. Широко используемая 12-тоновая равная темперация смягчает диэзис и, таким образом, не делает различия между двумя разными типами полутонов. С другой стороны, 19-тоновая равномерная темпераментность не смягчает эту запятую и, таким образом, различает два полутона.

Примеры:

12 ТЕТ смягчает диэзис, как и множество других запятых.
19 ТЕТ смягчает септимальный диезис и синтонную запятую , но не смягчает диэзис.
22 ТЕТ смягчает септимальную запятую Архита , но не смягчает септимальную диезис или синтонную запятую.
31 ТЕТ смягчает синтонную запятую, а также запятую, определяемую соотношением ⁠ 99 / 98 ⁠ , но не смягчает диезис, семеричный диезис или септимальную запятую Архита.

В следующей таблице указано количество используемых шагов, соответствующих различным интервалам в различных системах настройки. Нули указывают, что интервал представляет собой запятую (т. е. смягчается) в данном конкретном равном темпераменте. ^{[ нужны разъяснения ]} Все соотношения частот в первом столбце связаны со статьей в Википедии.

Интервал (отношение частот)	5 Т ЭДО	7 Т ЭДО	12 Т ЭДО	19 Т ЭДО	22 Т ЭДО	31 Т ЭДО	34 Т ЭДО	41 Т ЭДО	53 Т ЭДО	72 Т ЭДО
${\tfrac {\ 2\ }{1}}$	5	7	12	19	22	31	34	41	53	72
${\tfrac {\ 15\ }{8}}$	5	6	11	17	20	28	31	37	48	65
${\tfrac {\ 9\ }{5}}$	4	6	10	16	19	26	29	35	45	61
${\tfrac {\ 7\ }{4}}$	4	6	10	15	18	25	28	33	43	58
${\tfrac {\ 5\ }{3}}$	4	5	9	14	16	23	25	30	39	53
${\tfrac {\ 8\ }{5}}$	3	5	8	13	15	21	23	28	36	49
${\tfrac {\ 3\ }{2}}$	3	4	7	11	13	18	20	24	31	42
${\tfrac {\ 10\ }{7}}$	3	3	6	10	11	16	17	21	27	37
${\tfrac {\ 64\ }{45}}$	2	4	6	10	11	16	17	21	27	37
${\tfrac {\ 45\ }{32}}$	3	3	6	9	11	15	17	20	26	35
${\tfrac {\ 7\ }{5}}$	2	4	6	9	11	15	17	20	26	35
${\tfrac {\ 4\ }{3}}$	2	3	5	8	9	13	14	17	22	30
${\tfrac {\ 9\ }{7}}$	2	2	4	7	8	11	12	15	19	26
${\tfrac {\ 5\ }{4}}$	2	2	4	6	7	10	11	13	17	23
${\tfrac {\ 6\ }{5}}$	1	2	3	5	6	8	9	11	14	19
${\tfrac {\ 7\ }{6}}$	1	2	3	4	5	7	8	9	12	16
${\tfrac {\ 8\ }{7}}$	1	1	2	4	4	6	6	8	10	14
${\tfrac {\ 9\ }{8}}$	1	1	2	3	4	5	6	7	9	12
${\tfrac {\ 10\ }{9}}$	1	1	2	3	3	5	5	6	8	11
${\tfrac {\ 27\ }{25}}$	0	1	1	2	3	3	4	5	6	8
${\tfrac {\ 15\ }{14}}$	1	0	1	2	2	3	3	4	5	7
${\tfrac {\ 16\ }{15}}$	0	1	1	2	2	3	3	4	5	7
${\tfrac {\ 21\ }{20}}$	0	1	1	1	2	2	3	3	4	5
${\tfrac {\ 25\ }{24}}$	1	0	1	1	1	2	2	2	3	4
${\tfrac {\ 648\ }{625}}$	−1	1	0	1	2	1	2	3	3	4
${\tfrac {\ 28\ }{27}}$	0	1	1	1	1	2	2	2	3	4
${\tfrac {\ 36\ }{35}}$	0	0	0	1	1	1	1	2	2	3
${\tfrac {\ 128\ }{125}}$	−1	1	0	1	1	1	1	2	2	3
${\tfrac {\ 49\ }{48}}$	0	1	1	0	1	1	2	1	2	2
${\tfrac {\ 50\ }{49}}$	1	−1	0	1	0	1	0	1	1	2
${\tfrac {\ 64\ }{63}}$	0	0	0	1	0	1	0	1	1	2
${\tfrac {\ 531441\ }{524288}}$	1	−1	0	−1	2	−1	2	1	1	0
${\tfrac {\ 81\ }{80}}$	0	0	0	0	1	0	1	1	1	1
${\tfrac {\ 2048\ }{2025}}$	−1	1	0	1	0	1	0	1	1	2
${\tfrac {\ 126\ }{125}}$	−1	1	0	0	1	0	1	1	1	1
${\tfrac {\ 1728\ }{1715}}$	0	−1	−1	1	0	0	−1	1	0	1
${\tfrac {\ 2109375\ }{2097152}}$	3	−2	1	−1	0	0	1	−1	0	−1
${\tfrac {\ 15625\ }{15552}}$	2	−1	1	0	−1	1	0	−1	0	0
${\tfrac {\ 225\ }{224}}$	1	−1	0	0	0	0	0	0	0	0
${\tfrac {\ 32805\ }{32768}}$	1	−1	0	−1	1	−1	1	0	0	−1
${\tfrac {\ 2401\ }{2400}}$	−1	2	1	−1	1	0	2	0	1	0
${\tfrac {\ 4375\ }{4374}}$	−1	0	−1	0	1	−1	0	1	0	0

Запятую также можно считать дробным интервалом, остающимся после «полного круга» некоторого повторяющегося выбранного интервала; все повторяющиеся интервалы имеют одинаковый размер по относительной высоте, и все производимые тона понижаются или повышаются на целые октавы обратно до октавы, окружающей начальную высоту. Пифагорейская запятая, например, — это разница, полученная, скажем, между A ♭ и G ♯ после круга из двенадцати ровно пятых. Круг из трех только больших третей, например A ♭ CEG ♯ , образует малый диезис. ⁠ 128/125 ♭ цента ⁠ (41,1 ) G ♯ и A . между Круг из четырех второстепенных третей, например G ♯ BDFA ♭ , образует интервал ⁠ 648/625 том, что эта и т. д. Интересное свойство темпераментов состоит в ⁠ между A ♭ и G ♯ разница сохраняется при любой настройке интервалов, образующих круг. ^[11]В этом смысле запятые и тому подобные минутные интервалы никогда не могут быть полностью смягчены, какая бы настройка ни была.

Последовательность запятых

Последовательность запятых определяет музыкальный темперамент посредством уникальной последовательности запятых при возрастании простых чисел пределов . ^[12]Первая запятая последовательности запятых находится в $q$ -пределе, где $q$ — $n$ -е нечетное простое число (простое число 2 игнорируется, поскольку оно представляет октаву), а $n$ — количество образующих . Последующие запятые находятся в пределах простых чисел, каждая из которых является следующей по порядку простым числом над последней.

Другие интервалы, называемые запятыми

Есть также несколько интервалов, называемых запятыми, которые технически не являются запятыми, поскольку не являются рациональными дробями, подобными указанным выше, а являются их иррациональными аппроксимациями. К ним относятся запятые Холдриана и Меркатора, ^[13]и размер шага между тонами в 53 TET .

См. также

Ссылки

^ Уолдо Селден Пратт (1922). Словарь музыки и музыкантов Гроува , Vol. 1, с. 568. Джон Александр Фуллер Мейтленд , сэр Джордж Гроув , ред. Макмиллан.
^ Клайв Грейтед (2001). «Запятая», Grove Music Online . doi : 10.1093/gmo/9781561592630.article.06186
^ Бенсон, Дэйв (2006). Музыка: математическое предложение , с. 171. ISBN 0-521-85387-7 .
^ Галушка, Ян (2003). Математическая теория тональных систем . ЦРК Пресс. п. $XXVI$ . ISBN 0-8247-4714-3 .
↑ Перейти обратно: Перейти обратно: ^а ^б Раш, Рудольф (2000). «Пара слов о настройках Гарри Партча». В Данне, Дэвид (ред.). Гарри Партч: Антология критических взглядов . п. 34 . ISBN 90-5755-065-2 . — Описывает разницу между 11 предельными и 3 предельными интервалами.
^ Раш, Рудольф (1988). «Системы музыкальной интонации Фарея». В Бенитесе, Х.М.; и др. (ред.). Слушаю . Том. 2. п. 40. ИСБН 3-7186-4846-6 . = Источник для 32:33 как разница между 11:16 и 2:3 .
^ «Список запятых по простому пределу» . Ксенгармоническая вики .
^ см. статью «Расширенная нотация высоты звука Гельмгольца-Эллиса JI: метод записи натуральных интервалов» в журнале « Микротоны и многое другое» - «О гамбургских путях Дьёрдя Лигети» , изд. Манфреда Станке , Бокель Верлаг, Гамбург, 2005 г. ISBN 3-932696-62-Х
^ Статья в энциклопедии Tonalsoft об обозначении HEWM.
^ Джон Фонвилл . «Расширенная справедливая интонация Бена Джонстона - Руководство для переводчиков», с. 109, Перспективы новой музыки , т. 109, Перспективы новой музыки. 29, нет. 2 (лето 1991 г.), стр. 106–137. и Джонстон, Бен и Гилмор, Боб (2006). «Система обозначений для расширенной простой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , с. 78. ISBN 978-0-252-03098-7
^ Раш, Рудольф (2002). «Тюнинг и темперамент». В Кристенсене, Т. (ред.). Кембриджская история теории западной музыки . Издательство Кембриджского университета. п. 201. ИСБН 0-521-62371-5 .
^ Смит, Г.В. «Последовательности запятых» . Ксенгармония . Проверено 26 июля 2012 г. - через lumma.org.
^ Монзо, Джо. «Меркатора-запятая / Запятая Меркатора» . tonalsoft.com .

[1] Уолдо Селден Пратт (1922). Словарь музыки и музыкантов Гроува , Vol. 1, с. 568. Джон Александр Фуллер Мейтленд , сэр Джордж Гроув , ред. Макмиллан.

[2] Клайв Грейтед (2001). «Запятая», Grove Music Online . doi : 10.1093/gmo/9781561592630.article.06186

[3] Бенсон, Дэйв (2006). Музыка: математическое предложение , с. 171. ISBN 0-521-85387-7 .

[4] Галушка, Ян (2003). Математическая теория тональных систем . ЦРК Пресс. п. $XXVI$ . ISBN 0-8247-4714-3 .

[Rasch-5] Перейти обратно: Перейти обратно: ^а ^б Раш, Рудольф (2000). «Пара слов о настройках Гарри Партча». В Данне, Дэвид (ред.). Гарри Партч: Антология критических взглядов . п. 34 . ISBN 90-5755-065-2 . — Описывает разницу между 11 предельными и 3 предельными интервалами.

[6] Раш, Рудольф (1988). «Системы музыкальной интонации Фарея». В Бенитесе, Х.М.; и др. (ред.). Слушаю . Том. 2. п. 40. ИСБН 3-7186-4846-6 . = Источник для 32:33 как разница между 11:16 и 2:3 .

[7] «Список запятых по простому пределу» . Ксенгармоническая вики .

[8] см. статью «Расширенная нотация высоты звука Гельмгольца-Эллиса JI: метод записи натуральных интервалов» в журнале « Микротоны и многое другое» - «О гамбургских путях Дьёрдя Лигети» , изд. Манфреда Станке , Бокель Верлаг, Гамбург, 2005 г. ISBN 3-932696-62-Х

[9] Статья в энциклопедии Tonalsoft об обозначении HEWM.

[Fonville-10] Джон Фонвилл . «Расширенная справедливая интонация Бена Джонстона - Руководство для переводчиков», с. 109, Перспективы новой музыки , т. 109, Перспективы новой музыки. 29, нет. 2 (лето 1991 г.), стр. 106–137. и Джонстон, Бен и Гилмор, Боб (2006). «Система обозначений для расширенной простой интонации» (2003), «Максимальная ясность» и другие сочинения о музыке , с. 78. ISBN 978-0-252-03098-7

[11] Раш, Рудольф (2002). «Тюнинг и темперамент». В Кристенсене, Т. (ред.). Кембриджская история теории западной музыки . Издательство Кембриджского университета. п. 201. ИСБН 0-521-62371-5 .

[12] Смит, Г.В. «Последовательности запятых» . Ксенгармония . Проверено 26 июля 2012 г. - через lumma.org.

[13] Монзо, Джо. «Меркатора-запятая / Запятая Меркатора» . tonalsoft.com .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]