Квинтовый круг
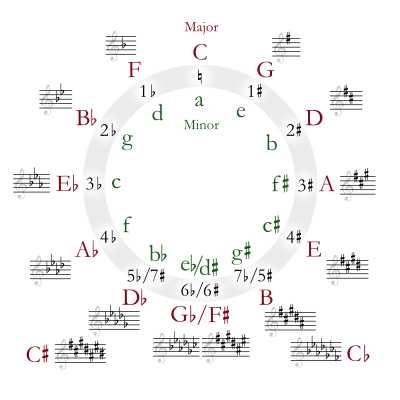
В теории музыки круг квинт представляет собой способ организации высоты звука как последовательность идеальных квинт . Начиная с ноты C и используя стандартную систему настройки для западной музыки ( 12 тонов равной темперации ), последовательность следующая: C, G, D, A, E, B, F ♯ (G ♭ ), C ♯ (D ♭ ), G ♯ (A ♭ ), D ♯ (E ♭ ), A ♯ (B ♭ ), E ♯ (F), C. В этом порядке наиболее тесно связанные ключевые подписи располагаются рядом друг с другом. Обычно его изображают в виде круга.
Двенадцатитоновая настройка равной темперации делит каждую октаву на двенадцать эквивалентных полутонов, а круг квинт приводит к ноте C на семь октав выше начальной точки. Если квинты настроены с точным соотношением 3:2 (система настройки, известная как просто интонация ), это не так (круг не «замыкается»).
Определение [ править ]
Круг квинт организует высоту звука в последовательность идеальных квинт , обычно изображаемую в виде круга с высотами звука (и соответствующими им клавишами) по часовой стрелке. Его можно рассматривать в направлении против часовой стрелки как круг четвертей. Гармонические прогрессии в западной музыке обычно используют соседние клавиши в этой системе, что делает ее полезным справочником по музыкальной композиции и гармонии. [1]
В верхней части круга показана тональность до мажор, без диезов и бемолей . Двигаясь по часовой стрелке, высота звука увеличивается на квинты. Сигнатуры клавиш, связанные с этими высотами, соответственно изменяются: тональность G имеет один диез, тональность D — 2 диеза и так далее. Против часовой стрелки от вершины круга ноты меняются по нисходящим квинтам и соответственно изменяются тональности: в тональности F одна бемоль, в тональности B ♭ — 2 бемоли и так далее. Некоторые клавиши (внизу круга) могут быть записаны как диезами, так и бемолями .
Начиная с любой высоты и поднимаясь на квинту, генерируются все тона, прежде чем вернуться к начальному классу высоты (класс высоты состоит из всех нот, обозначенных данной буквой, независимо от октавы - например, все ноты «C» принадлежат к тот же тональный класс). Двигаясь против часовой стрелки, высота звука понижается на квинту, но повышение на чистую кварту приведет к той же ноте на октаву выше (следовательно, к тому же классу высоты тона). Движение против часовой стрелки от C можно рассматривать как опускание на квинту до F или подъем на кварту до F.
Структура и использование [ править ]
Диатонические тональности [ править ]
Каждая высота звука может служить тоникой мажорной или минорной каждой из этих тональностей будет связана диатоническая гамма тональности, и с . На круговой диаграмме показано количество диезов или бемолей в каждой тональности , при этом мажорная тональность обозначается заглавной буквой, а минорная тональность — строчной буквой. Мажорные и второстепенные ключи, имеющие одинаковую сигнатуру, называются относительными мажорными и относительными второстепенными друг друга.
Модуляция и последовательность аккордов [ править ]
Тональная музыка часто модулируется в новый тональный центр, тональность которого отличается от оригинала только на один бемоль или диез. Эти тесно связанные тональности находятся на расстоянии одной квинты друг от друга и, следовательно, соседствуют в квинтовом круге. Последовательности аккордов также часто перемещаются между аккордами, корни которых связаны идеальной квинтой, что делает круг квинт полезным для иллюстрации «гармонического расстояния» между аккордами.

Квинтовый круг используется для организации и описания гармонической или тональной аккордов функции . [2] Аккорды могут развиваться по схеме восходящих чистых четвертей (поочередно рассматриваемых как нисходящие чистые квинты) в «функциональной последовательности». Это можно показать «... кругом квинт (в котором, следовательно, ступень II гаммы ближе к доминанте , чем ступень IV гаммы)». [3] С этой точки зрения тоника или тональный центр считается конечной точкой последовательности аккордов, полученной из квинтового круга.

Согласно книге Ричарда Франко Гольдмана « Гармония в западной музыке », «в простейших механизмах диатонических отношений IV аккорд находится на наибольшем расстоянии от I. С точки зрения [нисходящего] круга квинт он уводит от I, а не к этому». [4] Он утверждает, что прогрессия I–ii–V–I ( аутентичная каденция ) будет казаться более окончательной или решенной, чем I–IV–I ( плагальная каденция ). Голдман [5] согласен с Наттиезом, который утверждает, что «аккорд четвертой ступени появляется задолго до аккорда II и последующего финального I в прогрессии I – IV – VII». тот –iii–vi–ii–V–I», и там тоже дальше от тоники. [6] (В этой и связанных статьях римские цифры в верхнем регистре обозначают основные триады, а римские цифры в нижнем регистре — второстепенные триады.)
круга в неравных настройки системах Замыкание
Использование точного соотношения частот 3:2 для определения идеальной квинты ( просто интонации ) не совсем приводит к возврату к высоте звука начальной ноты после прохождения круга квинт. Двенадцатитоновая равнотемперированная настройка дает квинты, которые возвращаются к тону ровно на семь октав выше исходного тона и делают соотношение частот хроматического полутона таким же, как и диатонического полутона. Стандартная темперированная пятая часть имеет соотношение частот 2. 7/12 :1 (или около 1,498307077:1), примерно на два цента уже правильно настроенной квинты.
Восхождение на двенадцать правильно настроенных квинт не позволяет замкнуть круг на превышение примерно на 23,46 цента , примерно четверть полутона , интервал, известный как пифагорейская запятая . Если пифагорейский строй ограничен двенадцатью тонами на октаву, он заметно сокращает ширину одной из двенадцати пятых, что делает его сильно диссонирующим . Эту аномальную квинту называют волчьей квинтой – юмористическая отсылка к волку, выющему нестандартную ноту. Нерасширенная четверть-запятая означает, что используются одиннадцать пятых, немного уже, чем одинаково умеренная квинта, и требуется гораздо более широкая и даже более диссонирующая волчья пятая, чтобы замкнуть круг. Более сложные системы настройки, основанные только на интонации, такие как настройка с 5 пределами , используют не более восьми правильно настроенных квинт и как минимум три неправильных квинты (некоторые немного уже, а некоторые немного шире, чем только квинта), чтобы замкнуть круг.
Равнотемперированные строи с более нотами чем двенадцатью
В настоящее время, с появлением электронных изоморфных клавиатур , настройки равной темперации с более чем двенадцатью нотами на октаву могут использоваться для замыкания квинтового круга для других настроек. Например, равная темперация с 31 тоном близко соответствует среднему тону с четверть запятой, а равная темперация с 53 тонами близко соответствует пифагорейской настройке.
История [ править ]


Квинтовый круг возник в конце 1600-х и начале 1700-х годов для теоретизирования модуляции эпохи барокко (см. § Эпоха барокко ).
Диаграмма первого круга квинт появляется в « Грамматике» (1677) композитора и теоретика Николая Дилецкого , который намеревался представить теорию музыки как инструмент композиции. [7] Это был «первый в своем роде, направленный на то, чтобы научить российскую аудиторию писать полифонические композиции в западном стиле».
Диаграмма квинтового круга была независимо создана немецким композитором и теоретиком Иоганном Давидом Хейнихеном в его Ной-изобретенных и подробных инструкциях (1711 г.). [8] который он назвал «Музыкальный кружок» (нем. Musicalischer Circul ). [9] [10] Это было также опубликовано в его «Генерал-басе в композиции» (1728).
Хейнихен поместил относительную минорную тональность рядом с мажорной, что не отражало фактическую близость клавиш. Иоганн Маттесон (1735 г.) и другие пытались улучшить это - Дэвид Келлнер (1737 г.) предложил располагать основные клавиши в одном круге, а относительные второстепенные клавиши - во втором, внутреннем круге. Позже это было развито в хордовое пространство , включив также параллельный минор. [11]
Некоторые источники предполагают, что квинтовый круг был известен в древности Пифагору . [12] [13] [14] Это недоразумение и анахронизм. [15] Настройка по квинтам (так называемая пифагорейская настройка ) восходит к Древней Месопотамии; [16] см. « Музыка Месопотамии § Теория музыки» , хотя они не расширили ее до двенадцати нотной шкалы, остановившись на семи. Пифагорова запятая была вычислена Евклидом и китайскими математиками (в « Хуайнаньцзы »); см. запятую Пифагора § История . Таким образом, в древности было известно, что цикл из двенадцати квинт почти точно равен семи октавам (более практично, чередование восходящих квинт и нисходящих кварт составляет почти точно октаву). Однако это были теоретические знания, которые не использовались ни для построения повторяющейся двенадцатитоновой гаммы, ни для модуляции. Позже это было сделано с использованием средней темперации и двенадцатитоновой равной темперации , которые позволяли модулировать, сохраняя строй, но не получили развития в Европе примерно до 1500 года. Хотя он был популяризирован как квинтовый круг, его англосаксонское этимологическое происхождение восходит к название «квинтовое колесо».
Используйте [ править ]
В музыкальных произведениях эпохи барокко и классической эпохи музыки , а также в западной популярной музыке , традиционной музыке и народной музыке , когда пьесы или песни модулируются в новой тональности, эти модуляции часто связаны с квинтовым кругом.
На практике в композициях редко используется весь квинтовый круг. Чаще всего композиторы используют «композиционную идею «цикла» квинт, когда музыка последовательно движется через меньший или больший сегмент тональных структурных ресурсов, которые абстрактно представляет круг». [17] Обычной практикой является получение круга квинт из семи тонов диатонической гаммы, а не из всего диапазона двенадцати тонов, присутствующих в хроматической гамме. В этой диатонической версии круга одна из квинт не является настоящей квинтой: это тритон (или уменьшенная квинта), например, между F и B в «естественной» диатонической гамме (т. е. без диезов и бемолей). Вот как получается квинтовый круг путем перестановки диатонической мажорной гаммы:
И из (натурального) минора:
Ниже приводится основная последовательность аккордов, которые можно построить на основе основной басовой партии:
И над минором:
Добавление септаккордов к аккордам создает большее ощущение движения вперед в гармонии:
Эпоха барокко [ править ]
По словам Ричарда Тарускина , Арканджело Корелли был самым влиятельным композитором, сделавшим этот образец стандартным гармоническим «тропом» : «Именно во времена Корелли, в конце семнадцатого века, квинтовый круг «теоретизировался» как основной двигатель гармонического движения, и именно Корелли больше, чем кто-либо другой композитор, воплотил эту новую идею в впечатляющую практику». [18]
Квинтовый круг часто встречается в музыке И. С. Баха . Далее, из Jauchzet Gott в Allen Landen , BWV 51 , даже когда соло-басовая партия подразумевает, а не указывает задействованные аккорды:
Гендель использует последовательность квинт в качестве основы для части пассакальи из своей сюиты № 6 для клавесина соль минор.
Композиторы эпохи барокко научились усиливать «движущую силу» гармонии, порождаемой кругом квинт, «путем добавления септаккордов к большинству составляющих аккордов». «Эти седьмые, будучи диссонансами, создают потребность в разрешении, превращая, таким образом, каждую последовательность круга в одновременное облегчение и рестимулятор гармонического напряжения... Следовательно, они используются для выразительных целей». [19] Поразительные отрывки, иллюстрирующие использование седьмых, встречаются в арии «Pena tiranna» оперы Генделя 1715 года «Амадиги ди Гаула» :
Концерта – и в клавишной аранжировке Баха Алессандро Марчелло для гобоя и струнных .
Девятнадцатый век [ править ]
Экспромт ми-бемоль мажор Франца Шуберта , D 899, содержит гармонии, движущиеся по модифицированному кругу квинт:
из Часть Интермеццо Струнного Мендельсона квартета № 2 имеет короткий сегмент с квинтовым движением (ii° заменяется на iv):
В «Ребенке, засыпающем» Роберта Шумана из « Kinderszenen» используется прогрессия, изменяя ее в конце - пьеса заканчивается на аккорде ля минор вместо ожидаемого тоника ми минор.
В « опере Вагнера Götterdämmerung» в музыке присутствует цикл квинт, который переходит от конца пролога к первой сцене первого акта, действие которой происходит во внушительном зале богатых Гибихунгов. «Статус и репутация написаны во всех мотивах, присвоенных Гюнтеру», [20] вождь клана Гибичунг:
Джаз и популярная музыка [ править ]
Непреходящая популярность квинтового круга как формообразующего средства и как выразительного музыкального образа очевидна в количестве « стандартных » популярных песен, написанных в двадцатом веке. Джазовые музыканты также предпочитают его как средство импровизации, поскольку квинтовый круг помогает авторам песен понимать интервалы, соотношения аккордов и прогрессии.
Песня открывается набором нисходящих фраз – по сути, зацепкой песни – представленной с успокаивающей предсказуемостью, как будто будущее направление мелодии диктуется первыми пятью нотами. Гармоническая прогрессия, в свою очередь, редко выходит за пределы квинтового круга. [21]
- Джером Керн , « Все, чем ты являешься » [22]
- Рэй Ноубл , « Чероки ». Многим джазовым музыкантам это показалось особенно трудным, поскольку средние восьмерки очень быстро продвигаются по кругу, «создавая серию последовательностей II – V – I , которые временно проходят через несколько тональностей ». [23]
- Косма, Превер и Мерсер, « Осенние листья ». [24]
- Битлз , « Ты никогда не даешь мне своих денег » [25] [ нужен неосновной источник ]
- Майк Олдфилд , « Заклинания » [26]
- Карлос Сантана , « Европа (Крик Земли, Улыбка Небес) » [ нужна ссылка ]
- Глория Гейнор , « Я выживу » [27] [ нужен неосновной источник ]
- Мальчики из зоомагазина , « Это грех » [28] [ нужен неосновной источник ]
- Донна Саммер , « Люблю любить тебя, детка » [29] [ нужен неосновной источник ]
Связанные понятия [ править ]
Диатонический круг квинт [ править ]
Диатонический круг квинт — это круг квинт, охватывающий только члены диатонической гаммы. Следовательно, он содержит уменьшенную квинту до мажор между B и F. См. структуру подразумевает множественность .Круговая прогрессия обычно представляет собой круг квинт через диатонические аккорды, включая один уменьшенный аккорд . Круговая прогрессия до мажор с аккордами I – IV – vii. тот –iii–vi–ii–V–I показано ниже.
Хроматический круг [ править ]
Квинтовый круг тесно связан с хроматическим кругом , который также располагает равнотемперированные классы высоты звука определенной настройки в круговом порядке. Ключевое различие между двумя кругами заключается в том, что хроматический круг можно понимать как непрерывное пространство, где каждая точка круга соответствует мыслимому классу высоты тона , а каждый мыслимый класс высоты соответствует точке на круге. Напротив, квинтовый круг по своей сути представляет собой дискретную структуру, организованную через отдельные интервалы , и не существует очевидного способа назначить классы высоты звука для каждой из его точек. В этом смысле два круга математически совершенно различны.
Однако для любого положительного целого числа N классы высоты тона в N -тонах равной темперации могут быть представлены циклической группой порядка N или, что то же самое, классами остатков по модулю, равным N , . Группа имеет двенадцать тонов равной темпераментности. имеет четыре генератора, которые можно отождествить с восходящими и нисходящими полутонами, а также с восходящими и нисходящими чистыми квинтами. Генератор полутонов порождает хроматический круг , а чистая кварта и чистая квинта порождают квинтовый круг. В большинстве других строев, таких как 31 равнотемперированный , в качестве генератора можно использовать гораздо больше интервалов, и в результате возможно гораздо больше кругов.
Связь с хроматической гаммой [ править ]

Круг квинт или четвертей можно отобразить на основе хроматической гаммы путем умножения , и наоборот. Чтобы отобразить квинтовый круг и хроматическую гамму (в целочисленной записи ), умножьте на 7 ( M7 ), а для квинтового круга умножьте на 5 (P5).
В двенадцатитоновой равной темперации можно начать с упорядоченного кортежа из 12 ( тонального ряда ) целых чисел:
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
представляющие ноты хроматической гаммы: 0 = C, 2 = D, 4 = E, 5 = F, 7 = G, 9 = A, 11 = B, 1 = C ♯ , 3 = D ♯ , 6 = F ♯. , 8 знак равно г ♯ , 10 знак равно А ♯ . Теперь умножьте весь кортеж из 12 на 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
а затем примените сокращение по модулю 12 к каждому из чисел (вычтите 12 из каждого числа столько раз, сколько необходимо, пока число не станет меньше 12):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
что эквивалентно
- (C, G, D, A, E, B, F ♯ , C ♯ , G ♯ , D ♯ , A ♯ , F)
это квинтовый круг.Это энгармонически эквивалентно:
- (C, G, D, A, E, B, G ♭ , D ♭ , A ♭ , E ♭ , B ♭ , F).
спираль квинт , теоретические ключи и Энгармонические эквиваленты


В настройках равной темперации не используется точное соотношение частот 3: 2, которое определяет идеальную квинту, тогда как только интонация использует это точное соотношение. Восхождение на квинты при равной темпераментности приводит к возврату к исходному классу высоты тона - начиная с C и возрастая на квинты, после определенного количества итераций приводит к другому C. Этого не происходит, если используется точное соотношение 3:2 (только интонация). Регулировка, сделанная при равнотемперированной настройке, называется запятой Пифагора . Из-за этой разницы высота звука, энгармонически эквивалентная в равных темперациях (например, C ♯ и D ♭ в 12-тоновой равной темперации или C ♯ и D ![]() в 19 равный темперамент ) не эквивалентны при использовании только интонации.
в 19 равный темперамент ) не эквивалентны при использовании только интонации.
Таким образом, при простой интонации последовательность квинт можно визуализировать в виде спирали, а не круга - последовательность из двенадцати квинт приводит к « накачиванию запятой » пифагорейской запятой, визуализируемой как подъем на уровень вверх по спирали. См. также § Замыкание круга в неравных системах настройки .
Без энгармонических эквивалентов продолжение последовательности квинт приводит к образованию нот с двойными акциденциями (двойными диезами или двойными бемолью) или даже тройными или четверными акциденциями. В большинстве настроек с равной темперацией их можно заменить энгармонически эквивалентными нотами.
Ключи с двойными или тройными диезами и бемолями в тональностях называются теоретическими ключами ; они избыточны в 12-тоновой равнотемперации, поэтому их употребление крайне редко, но если число нот в октаве не кратно 12, их выделяют. Обозначения в этих случаях не стандартизированы.
Поведение LilyPond по умолчанию (на фото выше) записывает одинарные диезы или бемоли в порядке квинт, прежде чем переходить к двойным диеям или бемолям. Этот формат используется в Джона Фулда » «Всемирном реквиеме , соч. 60, [31] который заканчивается ключевой подписью G ♯ мажор, как показано выше. Диезы в ключевой подписи G ♯ мажор здесь продолжаются C ♯ , G ♯ , D ♯ , A ♯ , E ♯ , B ♯ , F ![]() .
.
Отдельные диез или бемоль в ключевой подписи иногда повторяются из вежливости, например, «Дополнение Макса Регера к теории модуляции» , которое содержит D ♭ минорные ключевые подписи на стр. 42–45 . У них есть B ♭ в начале, а также B. ![]() в конце (с двойным плоским символом) идут B ♭ , E ♭ , A ♭ , D ♭ , G ♭ , C ♭ , F ♭ , B
в конце (с двойным плоским символом) идут B ♭ , E ♭ , A ♭ , D ♭ , G ♭ , C ♭ , F ♭ , B ![]() . Соглашение LilyPond и Foulds подавило бы начальную B ♭ .Иногда в начале ключевой подписи пишутся двойные знаки, за которыми следуют одинарные знаки. Например, ключевая подпись F ♭ обозначается как B.
. Соглашение LilyPond и Foulds подавило бы начальную B ♭ .Иногда в начале ключевой подписи пишутся двойные знаки, за которыми следуют одинарные знаки. Например, ключевая подпись F ♭ обозначается как B. ![]() , Е ♭ , А ♭ , D ♭ , G ♭ , C ♭ , F ♭ . Это соглашение использует Виктор Эвальд, [32] программой Finale и некоторыми теоретическими работами.
, Е ♭ , А ♭ , D ♭ , G ♭ , C ♭ , F ♭ . Это соглашение использует Виктор Эвальд, [32] программой Finale и некоторыми теоретическими работами.
См. также [ править ]
- Подход к хорде
- Сонатная форма
- Ну темперамент
- Текстовая таблица круга пятых
- Созвездие высоты тона
- Мультипликативная группа целых чисел по модулю n
- Умножение (музыка)
- Круг третей
Примечания [ править ]
Ссылки [ править ]
- ↑ Майкл Пилхофер и Холли Дэй (23 февраля 2009 г.). «Квинтовый круг: краткая история» , www.dummies.com.
- ^ Брекхейс, Рожье (11 октября 2022 г.). «Квинтовое колесо – гармоническая функция» . Квинтовое колесо . Проверено 5 октября 2023 г.
- ^ Наттиез 1990 , с. 225.
- ^ Голдман 1965 , с. 68.
- ^ Goldman 1965 , глава 3.
- ^ Наттиез 1990 , с. 226.
- ^ Дженсен 1992 , стр. 306–307.
- ^ Иоганн Давид Хайнихен, Новое и тщательное обучение (1711), стр. 261
- ^ Барнетт 2002 , стр. 444.
- ^ Лестер 1989 , стр. 110–112.
- ^ Лердал, Фред (2005). Тональное пространство . Нью-Йорк: Издательство Оксфордского университета. п. 42. ИСБН 0195178297 .
- ^ «Полное руководство по пятому кругу!» . 17 января 2021 г.
- ^ «Круг пятых прояснился» .
- ^ «Челок – обучение стало проще» .
- ^ Фрейзер, Питер А. (2001), Разработка систем музыкальной настройки (PDF) , стр. 9, 13, заархивировано из оригинала (PDF) 1 июля 2013 г. , получено 24 мая 2020 г.
- ^ Дамбрил, Ричард Дж. (2005). Археомузыкология Древнего Ближнего Востока . Виктория, Британская Колумбия, с. 18. ISBN 978-1412055383 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Уиттолл, А. (2002, стр. 259) «Круг пятых», статья в Latham, E. (ред.) The Oxford Companion to Music . Издательство Оксфордского университета.
- ^ Тарускин 2010 , стр. 184.
- ^ Тарускин 2010 , с.
- ^ Скратон, Р. (2016, стр. 121) Кольцо истины: Мудрость Вагнера, Кольцо Нибелунга . Лондон, Аллен Лейн.
- ^ Джоя 2012 , с. 115.
- ^ Джоя 2012 , с. 16.
- ^ Скотт, Ричард Дж. (2003, стр. 123) Последовательности аккордов для авторов песен . Блумингтон, Индиана, Пресса Клуба писателей.
- ^ Костка, Стефан ; Пейн, Дороти; Альмен, Байрон (2013). Тональная гармония с введением в музыку двадцатого века (7-е изд.). Нью-Йорк: МакГроу-Хилл. стр. 46, 238. ISBN. 978-0-07-131828-0 .
- ^ «Ты никогда не даешь мне свои деньги» (1989, стр. 1099–1100, такты 1–16) Полные партитуры The Beatles . Хэл Леонард.
- ^ Оукс, Тим (июнь 1980 г.). «Майк Олдфилд» . Международный музыкант и мир звукозаписи . Проверено 19 февраля 2021 г. - через Tubular.net.
- ^ Фекарис, Д. и Перрен, Ф.Дж. (1978) «Я выживу». Международное издательство Полиграмма.
- ^ Теннант, Н. и Лоу, К. (1987, такты 1–8) «Это грех». Sony/ATV Music Publishing (UK) Ltd.
- ^ Мородер, Г. , Беллот, П. и Саммер, Д. (1975, такты 11–14) «Люблю любить тебя, детка» 1976, Bulle Music
- ^ Маккартин 1998 , стр. 364.
- ^ «Фолдс, Джон, Всемирный реквием , соч. 60, стр. 153 и далее» .
- ^ «Эвальд, Виктор, Квинтет № 4 ля ля ♭ , соч. 8 для духового квинтета [211.01]» .
Источники [ править ]
- Барнетт, Грегори (2002). «Тональная организация в теории музыки семнадцатого века». В Томасе Кристенсене (ред.). Кембриджская история теории западной музыки . Кембридж: Издательство Кембриджского университета. стр. 407–455.
- Джоя, Тед (2012). Джазовые стандарты: Путеводитель по репертуару . Издательство Оксфордского университета. ISBN 9780199769155 .
- Гольдман, Ричард Франко (1965). Гармония в западной музыке . Нью-Йорк: WW Нортон.
- Дженсен, Клаудия Р. (лето 1992 г.). «Теоретический труд Московии конца семнадцатого века: «Грамматика» Николая Дилецкого и ранний квинтовый кружок». Журнал Американского музыковедческого общества . 45 (2): 305–331. дои : 10.2307/831450 . JSTOR 831450 .
- Лестер, Джоэл (1989). Между модусами и ключами: немецкая теория 1592–1802 гг . Стуйвесант: Pendragon Press.
- Маккартин, Брайан Дж. (ноябрь 1998 г.). «Прелюдия к музыкальной геометрии» . Математический журнал колледжа . 29 (5): 354–370. дои : 10.1080/07468342.1998.11973971 . JSTOR 2687250 . Архивировано из оригинала 17 мая 2008 г. Проверено 29 июля 2008 г.
- Наттиез, Жан-Жак (1990). Музыка и дискурс: к семиологии музыки в переводе Кэролин Эббейт. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-02714-5 . (Первоначально опубликовано на французском языке под названием «Общая музыковедение и семиология» . Париж: К. Бургуа, 1987. ISBN 2-267-00500-X ).
- Тарускин, Ричард (2010). Оксфордская история западной музыки: музыка семнадцатого и восемнадцатого веков . Издательство Оксфордского университета.
Дальнейшее чтение [ править ]
- Д'Инди, Винсент (1903). Уроки музыкальной композиции . Париж: А. Дюран и др.
- Лестер, Джоэл. Между модусами и ключами: немецкая теория, 1592–1802 гг . 1990.
- Миллер, Майкл. Полное руководство идиота по теории музыки, 2-е изд . [Индианаполис, Индиана]: Альфа, 2005. ISBN 1-59257-437-8 .
- Пурвинс, Хендрик (2005). « Профили классов высоты звука: кругообразность относительной высоты звука и тональности - эксперименты, модели, вычислительный анализ музыки и перспективы ». доктор философии диссертация. Берлин: Технический университет Берлина .
- Пурвинс, Хендрик, Бенджамин Бланкерц и Клаус Обермайер (2007). « Тороидальные модели в теории тона и анализе высотных классов ». в: Вычисления в музыковедении 15 («Тональная теория для цифровой эпохи»): 73–98.
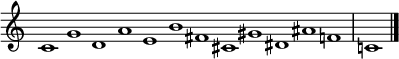







![{ << \new PianoStaff << \new Staff = "аккорды" << \magnifyStaff #2/3 \новый голос \relative c' { \key f \major \set Score.tempoHideNote = ##t \tempo 4 = 40 \time 3/4 \mark \markup { \abs-fontsize #10 { \bold { Адажио } } } d8 ддддд | эээээ | ггггг | \stemUp d'( f) \stemNeutral f( a) a( c16 bes) | bes2\mordent r4 | \перерыв c,8( e16 d) e8( g16 f) g8( bes16 a) | а2 \мордент r4 | bes,16( c32 a bes16 d32 cis) d16( e32 cis d16 f32 e) f16( g32 e f16 a32 g) | \перерыв g2 \мордент r4 | a,32( gis abab cis b) cis( d cis dedefefg! fgfge) | f4 \ мордент s4 } \новый голос \relative c' { с2. | s | \stemDown e8 ееее | f8 } \new Staff << \magnifyStaff #2/3 \новый голос \relative c' { \key f \major \clef F \time 3/4 Р2. | d8 ддддд | \stemUp цис-цис-цис-цис-цис | d <d f>[ <d f> <d f> <d f> <d f>] | <d f> <d f> <d f> <d f> <d f> <d f> | эээээ | <c e> <c e> <c e> <c e> <c e> <c e> | дддддд | <bes d> <bes d> <bes d> <bes d> <bes d> <bes d> | цис цис цис цис цис цис | д[ д] с4 } \новый голос \relative c' { \clef F с2. | s | \stemDown a8 ааааа | д, р р4 р | g8 гггг | c8 ccccc | е, фффф | бес-бес-бес-бес-бес-бес | е, ээээ | аааааа | д,[д]с4 } \addlyrics \with { alignAboveContext = "chords" } { \override LyricText.font-size = #-1.5 _ _ _ _ _ _ Dm \markup{\concat{Gm\super{7}}} _ _ _ _ _ C _ _ _ _ _ \markup{\concat{F\super{maj7}}} _ _ _ _ _ B♭ _ _ _ _ _ \markup{\concat{Em\super{7(♭5)}}} _ _ _ _ _ \markup{\concat{A\super{7}}} _ _ _ _ _ Dm }>> >> >>\новый персонал \с { \ опустить TimeSignature \magnifyStaff #2/3 первый ключ = ##f } \ относительно с' { \hide Staff.KeySignature \key f \major \clef bass {\stopStaff s2. ss \startStaff \hide Stem d8 sssssg, ssssscsssssf, ssss bes ssssse, ssssasssssd,}} >> }\layout { ширина строки = #150 }](http://upload.wikimedia.org/score/2/r/2rj0hc4pt0k6grm4sbdi8k7nqi1sdl7/2rj0hc4p.png)



![{<< \новый состав хора << \относительный с' { \magnifyStaff #3/4 \set Score.tempoHideNote = ##t \tempo 4 = 60 \time 3/4 \set Staff.midiInstrument = #"trumpet" \transposition f'^"in F" \p \grace {s16 s} ees2( d4) | ees2( d4) | цис2. ~ цис4-рр | Р2. | р | р | р | р | Р } \new Staff \with{\magnifyStaff #3/4 } << \new Voice \relative c' { \override Hairpin.minimum-length = #3 \set Staff.midiInstrument = #"trumpet" \transposition e'^"in E" \p \grace {s16 s} \hide \pp <g bes>2( <bes g>4) | <g bes>2( <bes g>4) | <bes d>4.( <g bes>8 <a c>4 | <bes d>2.) |<bes d>4.( <g bes>8 <a c>4 ) | <bes d>2 ееес4-! | c2._"(марк.)" | с2. | р | Р } \новый голос \relative c' { \stemDown \hide \p \grace {s16 s} s2. | s | s | s | s | с2 еес4-! | с2. | d4-! бес2 | Р2. | Р2. \бар "|." } >> >> \относительный с' { \magnifyStaff #3/4 \set Staff.midiInstrument = #"trombone" \transposition e^"in E" \p \grace {s16 s} \hide \pp g'2. ~ г ~ г ~ г | г~г2 бес4-! | g2._"(марк.)" | d'4-! бес2 | c2_"тусклый." р4 | \пп d2 r4 } \новый состав хора << \относительный с' { \magnifyStaff #3/4 \clef tenor \set Staff.midiInstrument = #"тромбон" \p \grace {s16 s} aes2( g4) | аес2( g4) | фис2. ~ фис | фис ~ фис2 b4-! | g2._"(марк.)" | цис4-! б2 | b2_"тусклый." р4 | \pp ais2 r4 } \относительный с' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"тромбон" \p \grace {s16 s} \hide \pp <b, d>2. | <б д> | <б д> ~ <б д> | <b d> ~ <b d>2 <b g'>4-! | <e g>2._"(марк.)" | <fis a>4-! <д фис>2 | <e g>_"тусклый." р4 | \pp <цис-фис>2 r4 } >> \относительный с' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"тромбон" \p \grace {s16 s} \hide \pp f,,!2( g4) | f!2( g4) | gis2. ~ гис | г! ~ g2 e4 ~ e a8._"(marc.)"[ g16 fis8. е16] | d2 g4( | цис,2_"разм.") r4 | \пп фис2 r4 } \относительный с' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"timpani" \p \grace {b,16 b} b4 rr | \ благодать {b16 b} b4 rr | \ благодать {b16 b} b4 rr | рбб | \ благодать {b16 b} b4 rr | рб ж' | б, р-р | Р2. | р | Р } \относительный с' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"tuba" \p \grace {s16 s} R2. | р | р | р | р | r4 re,, ~ e a8._"(marc.)"[ g16 fis8. е16] | d2 g4( цис,2_"тускл." ) r4 | \пп фис2 r4 } >> }\layout { ширина строки = #150 }](http://upload.wikimedia.org/score/b/9/b9cg7s9gxq732qwfg97n25bgulyaxon/b9cg7s9g.png)



