Круг третей
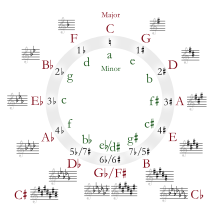
В теории музыки круг терций , также известный как цикл терций , представляет собой способ организации высоты тона и является основополагающим образцом в музыке . Этот цикл выражается через последовательность из 24 клавиш и, следовательно, нот , которые изменяются путем смещения вверх или вниз на мажорную или минорную терцию . Это, в свою очередь, приведет к заметному зрительному паттерну ( круг ) и слуховому паттерну (взаимосвязанным высотам), которые выводятся из хроматической гаммы . Начиная с C , цикл идет следующим образом: C, Em, G, Bm, D, F♯m, A, C♯m, E, G♯, B, D♯m, F♯/G♭, B♭m. , D♭, Fm, A♭, Cm, E♭, Gm, B♭, Dm, F, Am и обратно в C. [1] [а]
Круг терций образуется путем размещения нот мажорной или минорной гаммы в порядке терций, а не в порядке возрастания ступеней гаммы . Другими словами, этот образец не зависит от позиции в гамме, а скорее от последовательности терций. При использовании тональности, отличной от C, последовательность не будет начинаться с C, но она все равно будет в том же общем порядке, если рассматривать ее как круг. [2]
История
[ редактировать ]Происхождение
[ редактировать ]Понятие «третий круг» относительно новое в истории музыки. , конечно, не первый, кто его использовал, Популярный американский джазовый музыкант по имени Джон Колтрейн часто использовал цикл, состоящий из последовательности основных терций , для своих уникальных изменений тональности , отсюда и тезка « смены Колтрейна ». Его популярность в 1960-е годы, особенно благодаря его таким альбомам, как Bags & Trane , пролила свет на расширенные триады и в то же время на концепцию цикла терций. Эта концепция была в основном вдохновлена « изменениями Колтрейна », хотя и более развитыми. [3] [4]
Хотя точная дата появления термина «круг терций» неизвестна, вполне вероятно, что это произошло вскоре после смерти Джона Колтрейна в 1967 году. Тем не менее, круг терций и изменения Колтрейна продолжают использоваться во многих джазовых песнях, чтобы этот день, и, соответственно, вся музыка. [4]
Структура и современное использование
[ редактировать ]Весы
[ редактировать ]Круг терций, хотя и не так популярен, как круг квинт, тем не менее, имеет потенциал как полезный инструмент. В частности, этот цикл можно использовать как визуальный инструмент, помогающий запомнить порядок третей, минора и мажора в гамме, а также ноты любых аккордов в любой мажорной или минорной гамме . [2]
Вдобавок ко всему, цикл терций также может быть полезным инструментом для понимания связи между относительными тональностями . Потому что, как упомянуто ниже, цикл терций — это просто мажорные тональности квинтового круга, объединенные с их относительными второстепенными, и каждая клавиша имеет общую ключевую подпись с другой тональностью. Таким образом, можно получить приличное представление обо всех относительных тональностях и их обозначениях в нотной записи.
Аккорды
[ редактировать ]
В музыке круг терций может быть полезным для создания аккордов , а затем трезвучий и арпеджио . Это связано с тем, что многие аккорды построены на минорных и мажорных терциях. Например, мажорные аккорды состоят из единства интервалов большой терции и малой трети, в то время как минорные аккорды основаны на минорной терции и мажорной трети, уменьшенные аккорды - это две малые терции, а увеличенные аккорды - две мажорные терции. [б]
В качестве более практичного примера рассмотрим трезвучие до мажор, которое представляет собой просто сумму нот C, E, G в любом порядке. Расстояние ( интервал ) между C и E составляет четыре полутона , то есть большая терция. [5] Интервал между E и G составляет 3 полутона, то есть является второстепенной терцией. Как упоминалось в абзаце ниже, комбинация минорной трети и мажорной трети аналогична идеальной квинте, поэтому завершается все необходимое для создания аккорда до мажор, который является основной нотой (C), и следующих интервалов: мажорная треть (E) и чистая квинта (G). Это относится и к другим типам аккордов, упомянутым ранее, с той лишь разницей, как они построены и расположены.
Другое использование
[ редактировать ]Квинтовый круг
[ редактировать ]может Квинтовый круг действовать как подмножество терционного круга. Это связано с тем, что объединение мажорной трети (4 полутона/2 целых шага) с малой терцией (3 полутона) дает идеальную квинту (7 полутонов). Следовательно, последовательность отсчета каждой второй ноты в паттерне в цикле терций составит круг квинт. [1] Другими словами, если объединить мажорные тональности с их относительными минорными терциями (которые являются второстепенными терциями), можно получить модель терционного круга с включенным кругом квинт. [1]
Последовательности аккордов
[ редактировать ]Круг терций может быть полезным инструментом для понимания последовательности аккордов . Как и почему это происходит, можно посмотреть на тональность C и последовательность аккордов I—IV—V. Начиная с C, последовательность идет следующим образом: C—F—G. В круге третей F находится на два шага против часовой стрелки от C, а G также на два шага от C, но по часовой стрелке . Независимо от того, с какой тональности вы начинаете, они достигнут одного и того же рисунка, если это одна и та же последовательность аккордов.
См. также
[ редактировать ]- Квинтовый круг
- Основная треть
- Малая треть
- Хроматическая шкала
- Изменения Колтрейна
- Последовательность аккордов
Ссылки
[ редактировать ]Цитаты
[ редактировать ]- ^ Перейти обратно: а б с «Бреккерские свистки и флейты» . music.bracker.uk . Проверено 30 января 2024 г.
- ^ Перейти обратно: а б «Круг третей: визуальный инструмент для аккордов в мажорных и минорных гаммах» . отключено.io . Проверено 31 января 2024 г.
- ^ Мари, Йона (9 августа 2021 г.). «Круг третей — это что-то?» . Йона Мари Музыка .
- ^ Перейти обратно: а б «Объяснение изменений Колтрейна» . ТЖПС . Проверено 31 января 2024 г.
- ^ «Основы теории музыки 4: Трезвучия на гитаре» . Ноты на гитаре . 17.11.2021 . Проверено 6 февраля 2024 г.