53 равный темперамент

Рисунок 1: 53-TET в континууме настройки синтонного темперамента на отметке 701,89, из (Milne et al. 2007).

В музыке 53 равных темперамента , называемые 53 TET , 53 EDO или 53 ET , представляют собой темперированную гамму, полученную путем деления октавы на 53 равных шага (равных соотношения частот). Каждый шаг представляет соотношение частот 2 ^{1 ⁄ 53} , или 22,6415 центов ( ), интервал, который иногда называют холдровой запятой .

53-TET — это равнотемперированный строй , в котором темперированная чистая квинта имеет ширину 701,89 цента, как показано на рисунке 1.

Настройка 53-TET соответствует унисону или смягчает интервалы. 32805/32768 и , известный как раскол , 15625/15552 , клейсма как . известная Оба этих 5-предельных интервала включают в свою факторизацию только простые числа 2, 3 и 5, и тот факт, что 53 ET смягчает оба, полностью характеризует его как 5-предельный темперамент: это единственный правильный темперамент, смягчающий оба этих интервала. , или запятые , факт , который , кажется , был впервые признан японским теоретиком музыки Шохе Танакой . Поскольку он смягчает их, 53-ТЕТ может использоваться как для раскольнического темперамента , смягчающего раскол, так и для темперамента Хансона (также называемого клейсмическим), смягчающего клейсму.

Интервал 7 ⁄ 4 составляет 4,8 цента в 53-TET, и использование его для 7-предельной гармонии означает, что септимальная клеизма , интервал 225/224 , также закалено.

История и использование

Теоретический интерес к этому разделению восходит к античности. Цзин Фан (78–37 гг. до н.э.), китайский теоретик музыки, заметил, что ряд из 53 составляет всего лишь пятую часть ([ 3 ⁄ 2 ] ⁵³ ) почти равна 31 октаве (2 ³¹ ). Он вычислил эту разницу с точностью до шести цифр и составил 177147 ⁄ 176776 . Позднее такое же наблюдение сделал математик и теоретик музыки Николас Меркатор (ок. 1620–1687), вычисливший эту величину именно как (3 ⁵³ ) ⁄ (2 ⁸⁴ ) = 19383245667680019896796723 ⁄ 19342813113834066795298816 , которая известна как запятая Меркатора . Запятая Меркатора изначально имеет такое маленькое значение (≈ 3,615 цента), но 53 равных темперамента выравнивают каждую пятую лишь на 1 ⁄ 53 этой запятой (≈ 0,0682 цента ≈ 1 ⁄ 315   синтонная запятая ≈ 1/344 ) пифагорова   запятая . Таким образом, 53 равных тона темперации для всех практических целей эквивалентны расширенной пифагорейской настройке .

После Меркатора Уильям Холдер опубликовал в 1694 году трактат, в котором указывалось, что 53 равных темперамента также очень близко приближаются к основной терции (с точностью до 1,4 цента), и, следовательно, 53 равных темпераментов очень хорошо сочетаются с интервалами 5, ограничивающими только интонацию . Это свойство 53-ТЕТ могло быть известно ранее; Неопубликованные рукописи Исаака Ньютона позволяют предположить, что он знал об этом еще в 1664–1665 годах.

Музыка

В 19 веке люди начали разрабатывать инструменты 53 TET, рассчитывая использовать их для исполнения музыки с лимитом почти в 5 пределов . Такие инструменты были изобретены RHM Bosanquet. и американский тюнер JP White . Впоследствии темперамент время от времени использовался композиторами на Западе, и к началу 20 века 53 TET стал наиболее распространенной формой настройки в османской классической музыке , заменив ее старую неравную настройку. Арабская музыка , которая по большей части основывает свою теорию на четвертьтонах , также в некоторой степени использовала их; Сирийский скрипач и теоретик музыки Туфик Аль-Сабаг предложил вместо равного разделения октавы на 24 части использовать 24-нотную шкалу в 53 TET в качестве основной шкалы для арабской музыки.

Хорватский композитор Йосип Штолцер-Славенски написал одно произведение, которое никогда не публиковалось, которого используется Энгармониум Бозанке в первой части , под названием «Музыка для системы Natur-ton» . Кроме того, генерал Томпсон работал в сотрудничестве с лондонским производителем гитар Луи Панормо над созданием энгармонической гитары.

Обозначения

Обозначения, используемые в османской классической музыке, где тон разделен на 9 запятых.

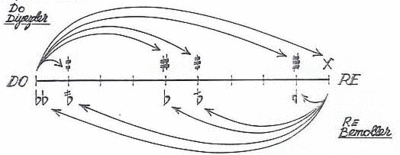
Попытка использовать стандартные обозначения, семибуквенные ноты плюс диез или бемоль, может быстро привести к путанице. Это не похоже на случай с 19 TET и 31 TET , где нет никакой двусмысленности. Не будучи подразумеваемым, это добавляет некоторые проблемы, которые требуют большего внимания. пифагорейскую мажорную терцию ( дитон В частности, различают ) и просто мажорную треть, а также пифагорейскую минорную терцию (полудитон) и просто минорную терцию. Тот факт, что синтонная запятая не умерена, означает, что ноты и интервалы необходимо определять точнее. Османская классическая музыка использует нотацию бемолей и диезов для тона с 9 запятыми.

Более того, поскольку 53 не кратно 12, такие ноты, как G ♯ и A ♭, не являются энгармонически эквивалентными, как и соответствующие ключевые знаки . В результате многие ключевые подписи потребуют использования двойных диезов (например, G ♯ мажор / E ♯ минор), двойных бемолей (например, F ♭ мажор / D ♭ минор) или микротональных изменений.

Расширенная пифагорейская нотация , использующая только диез и бемоль, дает следующую хроматическую гамму:

• С, Б ♯ , А ♯ , и , Д ♭ , С ♯ , Б , Ф , и ,
• Д, С , B ♯ , Ф , E ♭ , D ♯ , C ♯ , Г , F ♭ ,
• Э, Д , С /А , Г ,
• Ж, Е ♯ , Д ♯ , А , Г ♭ , Ж ♯ , Е , Д /Б , А ,
• Г, Ф , E ♯ , Б , A ♭ , G ♯ , F ♯ , С , Б ,
• А, Г , Ф /Д , С , B ♭ , A ♯ , G ♯ , Д , C ♭ ,
• Б, А , Г /И , Д , С

К сожалению, ноты заканчиваются, и требуется до четверных диезов и бемолей. В результате только большая третья должна быть записана как уменьшенная четвертая.

Обозначения взлетов и падений сохраняет ноты в порядке, а также сохраняет традиционное значение диез и бемоль. Он использует стрелки вверх и вниз, написанные в виде каретки или строчной буквы «v», обычно шрифтом без засечек. Одна стрелка равна одному шагу 53-TET. В названиях нот стрелки идут первыми, чтобы облегчить наименование аккордов. Множество энгармонических эквивалентов предоставляют большую свободу написания.

• C, ^C, ^^C, vvC ♯ /vD ♭ , vC ♯ /D ♭ , C ♯ /^D ♭ , ^C ♯ /^^D ♭ , vvD, vD,
• D, ^D, ^^D, vvD♯ / vE ♭ , vD♯ / E ♭ , D♯ , vvE /^E ♭ , ^ D♯ /^^E ♭ , vE,
• Е, ^Е, ^^Е/ввФ, вФ,
• F, ^F, ^^F, vvF ♯ /vG ♭ , vF ♯ /G ♭ , F ♯ /^G ♭ , ^F ♯ /^^G ♭ , vvG, vG,
• G, ^G, ^^G, vvG ♯ /vA ♭ , vG ♯ /A ♭ , G ♯ /^A ♭ , ^G ♯ /^^A ♭ , vvA, vA,
• A, ^A, ^^A, vvA ♯ /vB ♭ , vA ♯ /B ♭ , A ♯ /^B ♭ , ^A ♯ /^^B ♭ , vvB, vB,
• Б, ^B, ^^B/vvC, vC, C

Аккорды 53 равной темперации

Поскольку 53-TET — это пифагорейская система с почти чистыми квинтами, правильно интонированные мажорные и минорные трезвучия не могут быть написаны так же, как при средней тональной настройке. Вместо этого мажорные трезвучия представляют собой аккорды типа CF ♭ -G (с использованием обозначений, основанных на Пифагоре), где мажорная треть представляет собой уменьшенную кварту; это определяющая характеристика раскольнического темперамента . Точно так же минорные трезвучия представляют собой аккорды типа CD ♯ -G. В 53-TET доминирующий септаккорд будет писаться как CF ♭ -GB ♭ , но отональная тетрада будет CF ♭ -GC. , а CF ♭ -GA ♯ — это еще один септаккорд. Утональная -GG тетрада, инверсия отонной тетрады, пишется CD ♯ . .

Дальнейшие септимальные аккорды представляют собой уменьшенное трезвучие, имеющее две формы CD ♯ -G ♭ и CF. -G ♭ , субминорное трезвучие, CF -G, супермажорное триада CD -G и соответствующие тетрады CF -ГБ и компакт-диск -ГА ♯ . Поскольку 53-TET смягчает септимальную клейсму , септимальная клейсма дополнена триадой CF ♭ -B. в различных своих инверсиях также является аккордом системы. Так же и тетрада Оруэлла, CF ♭ -D -Г в различных его инверсиях.

Обозначения взлетов и падений допускают более традиционное написание. Поскольку он также называет интервалы 53-TET, он также предоставляет точные названия аккордов. Пифагоров минорный аккорд с терцией 32/27 до сих пор называется Cm и пишется C – E ♭ –G. Но в минорном аккорде с 5-лимитным пределом используется верхняя минорная 3-я 6/5 и пишется C–^E ♭ –G. Этот аккорд называется C^m. Сравните с ^Cm (^C–^E ♭ –^G).

• Мажорное трезвучие: C-vE-G (нижний мажор)
• Минорное трезвучие: C-^E ♭ -G (верхний минор)
• Доминантный 7-й номер: C-vE-GB ♭ (дополнение-7 вниз)
• Отональная тетрада: C-vE-G-vB ♭ (вниз7)
• Utonal tetrad: C-^E ♭ -G-^A (upminor6)
• Уменьшенная триада: C-^E ♭ -G ♭ (увеличенное значение)
• Уменьшенная триада: C-vE ♭ -G ♭ (тусклый)
• Субминорная триада: C-vE ♭ -G (нижний минор)
• Супермажорное триада: C-^EG (верхний мажор)
• Subminor tetrad: C-vE ♭ -G-vA (downminor6)
• Supermajor tetrad: C-^E-G-^B ♭ (up7)
• Дополненная триада: C-vE-vvG ♯ (downaug dud-5)
• Триада Оруэлла: C-vE-vvG-^A (мажорный dud-5 up6)

Поскольку 53-TET совместим как с раскольническим, так и с синтоническим темпераментом , его можно использовать в качестве основной настройки при модуляции темперамента (музыкальный эффект, создаваемый динамической тональностью ).

Размер интервала

7-Ограничьте только интонационные интервалы, аппроксимированные в 53-ET.

Поскольку расстояние в 31 ступень в этой гамме почти точно равно идеальной квинте , теоретически эту гамму можно считать слегка смягченной формой пифагорейской настройки , расширенной до 53 тонов. Таким образом, доступные интервалы могут иметь те же свойства, что и любой пифагорейский строй, например, квинты, которые являются (практически) чистыми, мажорные терции, которые широки от всего (около 81 ⁄ 64 в отличие от более чистого 5 ⁄ 4 и малые трети, которые наоборот узкие ( 32 ⁄ 27 по сравнению с 6 ⁄ 5 ).

Однако 53-ТЕТ содержит дополнительные интервалы, очень близкие к просто интонации. Например, интервал в 17 шагов тоже является большой терцией, но лишь на 1,4 цента уже очень чистого простого интервала. 5 ⁄ 4 . 53-ТЕТ очень хорош в качестве аппроксимации любого интервала в 5, ограничивая только интонацией. Аналогично, чистый справедливый интервал 6 ⁄ 5 всего на 1,3 цента шире, чем 14 шагов в 53-TET.

Совпадения с точными интервалами, включающими 7-ю гармонику, немного менее близки (43 шага составляют 4,8 цента для 7 ⁄ 4 ), но все такие интервалы по-прежнему довольно точно совпадают, причем наибольшее отклонение соответствует 7/5 ​ тритона . 11-я гармоника и входящие в нее интервалы менее точно совпадают, о чем свидетельствуют недесятичные нейтральные секунды и трети в таблице ниже. Передаточные числа 7 пределов окрашены в светло-серый цвет, а передаточные числа 11 и 13 пределов — в темно-серый цвет.

Размер ( шаги )	Размер (центов)	Название интервала	Только соотношение	Только (центов)	Ошибка (центов)	Лимит
53	1200.00	идеальная октава	2:1	1200.00	0	2
48	1086.79	классический мажорный септак	15:8	1088.27	−1.48	5
45	1018.87	просто второстепенная седьмая	9:5	1017.60	+1.27	5
44	996.23	Пифагорейская минорная седьмая	16:9	996.09	+0.14	3
43	973.59	гармоническая седьмая	7:4	968.83	+4.76	7
39	883.02	мажорная шестая	5:3	884.36	−1.34	5
37	837.73	трехзначный нейтральный шестой	13:8	840.53	−2.8	13
36	815.09	малая шестая	8:5	813.69	+1.40	5
31	701.89	идеальная пятая часть	3:2	701.96	−0.07	3
30	679.25	могила пятая	40:27	680.45	−1.21	5
27	611.32	Пифагорейская дополненная четвертая	729:512	611.73	−0.41	3
26	588.68	диатонический тритон	45:32	590.22	−1.54	5
26	588.68	семимальный тритон	7:5	582.51	+6.17	7
25	566.04	классический тритон	25:18	568.72	−2.68	5
24	543.40	недесятичный старший четвертый	11:8	551.32	−7.92	11
24	543.40	пятая уменьшенная вдвое	512:375	539.10	+4.30	5
24	543.40	недесятичная дополненная четвертая	15:11	536.95	+6.45	11
23	520.76	острая четвертая	27:20	519.55	+1.21	5
22	498.11	идеальная четвертая	4:3	498.04	+0.07	3
21	475.47	могила четвертая	320:243	476.54	−1.07	5
21	475.47	септимальная узкая четвертая	21:16	470.78	+4.69	7
20	452.83	классическая дополненная треть	125:96	456.99	−4.16	5
20	452.83	трехдесятичная дополненная треть	13:10	454.21	−1.38	13
19	430.19	семеричная большая треть	9:7	435.08	−4.90	7
19	430.19	классическая уменьшенная четвертая часть	32:25	427.37	+2.82	5
18	407.54	Пифагорейские тона	81:64	407.82	−0.28	3
17	384.91	просто главная треть	5:4	386.31	−1.40	5
16	362.26	серьезная мажорная треть	100:81	364.80	−2.54	5
16	362.26	нейтральная третья , трехдесятичная	16:13	359.47	+2.79	13
15	339.62	нейтральная треть , недесятичная	11:9	347.41	−7.79	11
15	339.62	острая малая треть	243:200	337.15	+2.47	5
14	316.98	просто второстепенная треть	6:5	315.64	+1.34	5
13	294.34	Пифагорейский полудитон	32:27	294.13	+0.21	3
12	271.70	классическая дополненная секунда	75:64	274.58	−2.88	5
12	271.70	семимальная малая треть	7:6	266.87	+4.83	7
11	249.06	классическая уменьшенная треть	144:125	244.97	+4.09	5
10	226.41	семимерный целый тон	8:7	231.17	−4.76	7
10	226.41	уменьшенная треть	256:225	223.46	+2.95	5
9	203.77	целый тон , мажорный тон	9:8	203.91	−0.14	3
8	181.13	целый тон, минорный тон	10:9	182.40	−1.27	5
7	158.49	нейтральная секунда , большая десятичная дробь	11:10	165.00	−6.51	11
7	158.49	серьезный весь тон	800:729	160.90	−2.41	5
7	158.49	нейтральная секунда , меньшая десятичная дробь	12:11	150.64	+7.85	11
6	135.85	мажорный диатонический полутон	27:25	133.24	+2.61	5
5	113.21	Пифагорейский мажорный полутон	2187:2048	113.69	−0.48	3
5	113.21	просто диатонический полутон	16:15	111.73	+1.48	5
4	90.57	основной клей	135:128	92.18	−1.61	5
4	90.57	Пифагорейский минорный полутон	256:243	90.22	+0.34	3
3	67.92	просто хроматический полутон	25:24	70.67	−2.75	5
3	67.92	больший диезис	648:625	62.57	+5.35	5
2	45.28	просто диэзис	128:125	41.06	+4.22	5
1	22.64	синтонная запятая	81:80	21.51	+1.14	5
0	0.00	идеальный унисон	1:1	0.00	0.00	1

Масштабная диаграмма

Ниже представлена ​​21 из 53 нот хроматической гаммы. Остальное можно легко добавить.

Интервал (шаги)		3		2		4		3		2		3		2		1		2		4		1		4		3		2		4		3		2		3		2		1		2
Интервал (центов)		68		45		91		68		45		68		45		23		45		91		23		91		68		45		91		68		45		68		45		23		45
Название ноты (нотация Пифагора)	С		И		C ♯		Д		Ф		D ♯		F ♭		Д		С /А		Ф		G ♭		F ♯		Г		Б		G ♯		Б		С		A ♯		C ♭		А		Г /И		С
Название ноты (обозначение подъемов и падений)	С		vvC ♯ /vD ♭		C ♯ /^D ♭		Д		vvD ♯ /vE ♭		D ♯ /^E ♭		вЕ		^Э		^^E/ввФ		Ф		vF ♯ /G ♭		F ♯ /^G ♭		Г		vvG ♯ /vA ♭		G ♯ /^A ♭		и А		vvA ♯ /vB ♭		A ♯ /^B ♭		вБ		^ Б		^^B/vvC		С
Примечание (центов)	0		68		113		204		272		317		385		430		453		498		589		611		702		770		815		883		974		1018		1087		1132		1155		1200
Примечание (шаги)	0		3		5		9		12		14		17		19		20		22		26		27		31		34		36		39		43		45		48		50		51		53

Холдрова запятая

В теории музыки и музыкальной настройке запятая Холдриана , также называемая запятой Гельдера , и редко арабская запятая , представляет собой небольшой музыкальный интервал примерно 22,6415 центов , равен одному шагу из 53 равных темпераментов, или ${\sqrt[{53}]{2}}$ ( ). Название «запятая» вводит в заблуждение, поскольку этот интервал является иррациональным числом и не описывает компромисс между интервалами какой-либо системы настройки; он получил это название, потому что это приближение к синтонной запятой (21,51 цента) ( ), который широко использовался в качестве меры настройки во Уильяма Холдера времена .

Происхождение запятой Гёльдера связано с тем, что древние греки (или, по крайней мере, Боэций) ) считал, что в пифагорейской настройке тон можно разделить на девять запятых, четыре из которых образуют диатонический полутон, а пять - хроматический полутон. Если все эти запятые будут одинакового размера, то получится октава из 5 тонов + 2 диатонических полутона, 5×9 + 2×4 = 53 равных запятых. Держатель деление октавы на 53 равные части приписывает Николаю Меркатору , кто бы назвал 1/53 часть октавы «искусственной запятой».

Запятая Меркатора и запятая Холдриа.

Запятая Меркатора — это имя, которое часто используется для обозначения близкого интервала из-за его связи с Николасом Меркатором. Один из этих интервалов был впервые описан Цзин-Фангом в 45 г. до н.э. Меркатор применил логарифмы, чтобы определить, что ${\sqrt[{55}]{2}}$ (≈ 21,8182 цента) было почти эквивалентно синтонной запятой ≈ 21,5063 цента (особенность преобладающего среднего темперамента в то время ). Он также считал, что «искусственная запятая» ${\sqrt[{53}]{2}}$ может быть полезно, потому что 31 октаву можно практически аппроксимировать циклом из 53 квинт . Уильям Холдер , в честь которого названа запятая Холдриана, отдавал предпочтение этой последней единице, потому что интервалы 53 равного темперамента ближе к простой интонации, чем интервалы 55. Таким образом, запятая Меркатора и запятая Холдриана представляют собой два разных, но связанных интервала.

Использование в турецкой теории макама

Холдрианская запятая использовалась в основном в османско-турецкой теории музыки Кемалем Илеричи и турецким композитором Эролом Саяном . Название этой запятой по-турецки — Holder koması .

Название интервала	Запятые	центы	Символ
Приходить	1	22.64	Ф
Баланс	4	90.57	Б
Маленький Мюценнеп	5	113.21	С
Великий Великолепный	8	181.13	К
Танины	9	203.77	Т
Сейчас декабрь (12)	12	271.70	А (12)
Сейчас декабрь (13)	13	294.34	А (13)

Например, Раст-макам (похожий на западную мажорную гамму или, точнее, на правильно настроенную мажорную гамму ) можно рассматривать с точки зрения холдровых запятых:

где обозначает холдровскую запятую, в отличие от макама Нихавенда (похожего на западную минорную гамму ):

где ♭ обозначает квартиру с пятью запятыми,имеет средние секунды между d–e ♭ , e–f , g–a ♭ , a ♭ – b ♭ и b ♭ – c' , причем средняя секунда находится где-то между 8 и 9 запятыми.

Ссылки

• Холдер, Уильям (1967) [1694]. Трактат о естественных основах и принципах гармонии (факсимиле). Нью-Йорк, штат Нью-Йорк: Братья Броуд. стр. 103–106.

Внешние ссылки

• Роджерс, Прент (май 2007 г.). «Песня-шепот в 53 ЭДО» . Bumper Music (подкаст) (медленная ред.).
• Хэнсон, Ларри (1989). «Разработка 53-тональной раскладки клавиатуры» (PDF) . Ксенгармоникон XII . Ганновер, Нью-Хэмпшир: Музыка Frog Peak: 68–85 . Получено 4 января 2021 г. - через Anaphoria.com.
• «Алгебра тональных функций» . Сонантометрия (блог). 01.05.2007. Тональные функции как степени 53-TET.
• Барбьери, Патрицио (2008). «Энгармонические инструменты и музыка, 1470–1900» . Латина, Il Levante Libreria Editrice . Италия. Архивировано из оригинала 15 февраля 2009 г.
• Кукула, Джим (август 2005 г.). «Равная темперация с 53 тонами на октаву» . Взаимозависимая наука . Фрактальная микротональная музыка . Проверено 4 января 2021 г.