Изменение вертикального давления

Вертикальное изменение давления — это изменение давления в зависимости от высоты . В зависимости от рассматриваемой жидкости и контекста, о котором идет речь, она также может значительно различаться по размерам, перпендикулярным высоте, и эти изменения имеют значение в контексте силы градиента давления и ее эффектов. Однако вертикальные изменения особенно значительны, поскольку они возникают в результате действия силы тяжести на жидкость; а именно, для одной и той же жидкости уменьшение высоты внутри нее соответствует более высокому столбу жидкости, давящему на эту точку.

Основная формула

Относительно простая версия ^[1] Вертикальное изменение давления жидкости заключается в том, что разница давлений между двумя высотами является продуктом изменения высоты, силы тяжести и плотности . Уравнение выглядит следующим образом: ${\frac {dP}{dh}}=-\rho g,$ где

$P$ – давление,
$ρ$ – плотность,
$g$ – ускорение свободного падения , а
$h$ — высота.

Символ дельты указывает на изменение данной переменной. Поскольку $g$ отрицательно, то увеличение высоты будет соответствовать уменьшению давления, что согласуется с приведенными ранее рассуждениями о весе столба жидкости.

Когда плотность и сила тяжести примерно постоянны (то есть при относительно небольших изменениях высоты), простое умножение разницы высот, силы тяжести и плотности даст хорошее приближение разницы давлений. Если известно, что давление в одной точке жидкости с однородной плотностью ρ равно P ₀ , то давление в другой точке равно P ₁ :

P_{1}=P_{0}-\rho g(h_{1}-h_{0})

где h ₁ - h ₀ — вертикальное расстояние между двумя точками. ^[2]

Если разные жидкости наслаиваются друг на друга, общая разница давлений будет получена путем сложения двух разностей давлений; первый - от точки 1 до границы, второй - от границы до точки 2; что потребует просто замены $значений ρ$ и $Δ h$ для каждой жидкости и суммирования результатов. Если плотность жидкости меняется с высотой, математическое интегрирование потребуется .

Можно ли обоснованно аппроксимировать плотность и гравитацию как постоянные, зависит от необходимого уровня точности , а также от масштаба разницы высот, поскольку сила тяжести и плотность также уменьшаются с увеличением высоты. В частности, рассматриваемая жидкость также важна для плотности; морская вода , например, считается несжимаемой жидкостью ; его плотность может меняться с высотой, но гораздо менее существенно, чем у воздуха. Таким образом, плотность воды можно более разумно считать постоянной, чем плотность воздуха, и при одинаковой разнице высот перепады давления в воде примерно равны на любой высоте.

Гидростатический парадокс

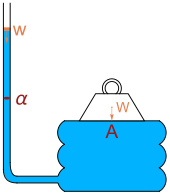
Барометрическая формула зависит только от высоты камеры с жидкостью, а не от ее ширины или длины. При достаточно большой высоте можно достичь любого давления. Эта особенность гидростатики получила название гидростатического парадокса . Как выразился В. Х. Безант , ^[3]

Любое количество жидкости, каким бы малым оно ни было, может выдержать любой вес, каким бы большим он ни был.

Фламандский ученый Саймон Стевин был первым, кто математически объяснил парадокс. ^[4] В 1916 году Ричард Глейзбрук упомянул гидростатический парадокс, описывая устройство, которое он приписывал Паскалю : тяжелый груз $W$ лежит на доске, площадь $А$ опирается на пузырек с жидкостью, соединенный с вертикальной трубкой с площадью поперечного сечения α. воду массой $w,$ Если вылить в трубку в конечном итоге поднимется тяжелый груз. Баланс сил приводит к уравнению

W={\frac {wA}{\alpha }}.

Глейзбрук говорит: «Сделав площадь доски значительной, а площадь трубки — маленькой, большой вес $W$ можно удержать на небольшом весе $воды w$ . Этот факт иногда называют гидростатическим парадоксом». ^[5]

Гидравлическое оборудование использует это явление для увеличения силы или крутящего момента. Демонстрация гидростатического парадокса используется при обучении этому явлению. ^[6]^[7]

В контексте атмосферы Земли

Если проанализировать изменение вертикального давления в атмосфере Земли , то масштаб длины очень значителен ( одна только тропосфера в несколько километров имеет высоту ; термосфера - несколько сотен километров), а участвующая в этом жидкость (воздух) сжимаема. Гравитацию все еще можно разумно считать постоянной, поскольку масштабы длины порядка километров все еще малы по сравнению с радиусом Земли, который в среднем составляет около 6371 км. ^[8] а гравитация является функцией расстояния от ядра Земли. ^[9]

С другой стороны, плотность более существенно меняется с высотой. следует, Из закона идеального газа что $\rho ={\frac {mP}{kT}},$ где

$m$ — средняя масса воздуха молекулы ,
$P$ – давление в данной точке,
$k$ — постоянная Больцмана ,
$Т$ — температура в Кельвинах .

Проще говоря, плотность воздуха зависит от атмосферного давления. Учитывая, что давление воздуха также зависит от плотности воздуха, легко могло бы сложиться впечатление, что это круговое определение , но это просто взаимозависимость различных переменных. Тогда это дает более точную формулу вида $P_{h}=P_{0}e^{-{\frac {mgh}{kT}}},$ где

$P h$ – давление на высоте $h$ ,
$P 0$ — давление в контрольной точке 0 (обычно относится к уровню моря),
$m$ — масса молекулы воздуха,
$g$ — ускорение свободного падения ,
$h$ — высота от контрольной точки 0,
$k$ — постоянная Больцмана ,
$Т$ — температура в Кельвинах.

Таким образом, вместо того, чтобы давление было линейной функцией высоты, как можно было бы ожидать от более простой формулы, приведенной в разделе «Основная формула», оно более точно представляется как экспоненциальная функция высоты.

Обратите внимание, что в этом упрощении температура считается постоянной, хотя температура также меняется с высотой. Однако изменение температуры в нижних слоях атмосферы ( тропосфера , стратосфера ) составляет лишь десятки градусов, в отличие от их термодинамической температуры , которая исчисляется сотнями, поэтому изменение температуры достаточно мало и поэтому игнорируется. При небольших перепадах высот, в том числе сверху вниз даже в самых высоких зданиях (таких как Си-Эн Тауэр ) или в горах сопоставимого размера, изменение температуры легко будет в пределах однозначных цифр. (См. также процент ошибок .)

Альтернативный вывод, показанный Портлендским государственным аэрокосмическим обществом, ^[10] Вместо этого используется для определения высоты как функции давления. Это может показаться нелогичным, поскольку давление зависит от высоты, а не наоборот, но такая формула может быть полезна при определении высоты на основе разницы давления, когда известно последнее, а не первое. Для разных видов приближений представлены разные формулы; для сравнения с предыдущей формулой первой в статье будет ссылка на ту же формулу, в которой применяется то же приближение постоянной температуры; в этом случае: $z=-{\frac {RT}{g}}\ln {\frac {P}{P_{0}}}$ где (со значениями, использованными в статье)

$z$ — высота в метрах,
$R$ — удельная газовая постоянная = 287,053 Дж/(кг·К).
$Т$ — абсолютная температура в Кельвинах = 288,15 К на уровне моря,
$g$ — ускорение свободного падения = 9,806· 65 м/с. ² на уровне моря,
$P$ — давление в данной точке на высоте $z$ в Паскалях , и
$P 0$ — давление в контрольной точке = 101325 Па на уровне моря.

Более общая формула, полученная в той же статье, учитывает линейное изменение температуры в зависимости от высоты (ступень градиента) и сводится к вышеуказанному, когда температура постоянна: $z={\frac {T_{0}}{L}}\left(\left({\frac {P}{P_{0}}}\right)^{-{\frac {LR}{g}}}-1\right)$ где

$L$ - градиент атмосферы (изменение температуры, разделенное на расстояние) = -6,5 × 10. ⁻³ К/м и
$T 0$ – температура в той же контрольной точке, для которой $P = P 0$

а остальные величины такие же, как указано выше. Это рекомендуемая формула для использования.

См. также

Ссылки

^ «Барометрическая формула» .
^ Стритер, Виктор Л. (1966). Механика жидкости , 4-е издание, стр.28, McGraw-Hill.
^ Безант, WH (1900). Элементарная гидростатика . Джордж Белл и сыновья . п. 11 – через Интернет-архив .
^ Ру, Софи (25 сентября 2012 г.). Механизация натуральной философии . Springer Science & Business Media. п. 160. ИСБН 978-9400743458 . Стевин предлагает оригинальную математическую демонстрацию так называемого гидростатического парадокса.
^ Глейзбрук, Ричард (1916). Гидростатика: Элементарный учебник, теоретический и практический . Издательство Кембриджского университета . п. 42 – через Интернет-архив .
^ Гринслейд-младший, Томас Б. «Гидростатический парадокс» . Кеньонский колледж .
^ Объяснение на YouTube
^ «Радиус Земли» . 2 марта 2009 г.
^ «Закон гравитации Ньютона» . www.splung.com . Проверено 23 июня 2023 г.
^ «Краткий вывод, связывающий высоту с давлением воздуха» (PDF) . Архивировано из оригинала (PDF) 28 сентября 2011 г. Проверено 30 ноября 2011 г.

Мерлино, Роберт Л. (2003). «Статика – жидкости в состоянии покоя» . Проверено 20 ноября 2014 г.

Внешние ссылки

СМИ, связанные с гидростатическим парадоксом, на Викискладе?

[1] «Барометрическая формула» .

[2] Стритер, Виктор Л. (1966). Механика жидкости , 4-е издание, стр.28, McGraw-Hill.

[3] Безант, WH (1900). Элементарная гидростатика . Джордж Белл и сыновья . п. 11 – через Интернет-архив .

[4] Ру, Софи (25 сентября 2012 г.). Механизация натуральной философии . Springer Science & Business Media. п. 160. ИСБН 978-9400743458 . Стевин предлагает оригинальную математическую демонстрацию так называемого гидростатического парадокса.

[5] Глейзбрук, Ричард (1916). Гидростатика: Элементарный учебник, теоретический и практический . Издательство Кембриджского университета . п. 42 – через Интернет-архив .

[6] Гринслейд-младший, Томас Б. «Гидростатический парадокс» . Кеньонский колледж .

[7] Объяснение на YouTube

[8] «Радиус Земли» . 2 марта 2009 г.

[9] «Закон гравитации Ньютона» . www.splung.com . Проверено 23 июня 2023 г.

[10] «Краткий вывод, связывающий высоту с давлением воздуха» (PDF) . Архивировано из оригинала (PDF) 28 сентября 2011 г. Проверено 30 ноября 2011 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]