Температура

Температура
Температура
	Тепловая вибрация сегмента альфа-спирали белка . Его амплитуда увеличивается с температурой
Общие символы	Т
И объединились	К
Другие подразделения	°C , °F , °R , °Rø , °Ré , °N , °D , °L , °W
Интенсивный ?	Да
Выводы из ; другие количества	,
Измерение

Температура – это физическая величина , количественно выражающая признак жары или холода. Температуру измеряют термометром . Он отражает среднюю кинетическую энергию колеблющихся и сталкивающихся атомов, составляющих вещество.

Термометры калибруются по различным температурным шкалам , которые исторически основывались на различных контрольных точках и термометрических веществах для определения. Наиболее распространенными шкалами являются шкала Цельсия с символом единицы °C (ранее называвшаяся стоградусной ), шкала Фаренгейта (°F) и шкала Кельвина (K), причем последняя используется преимущественно в научных целях. Кельвин — одна из семи основных единиц Международной системы единиц (СИ).

Абсолютный ноль , то есть ноль Кельвина или -273,15 °C, является самой низкой точкой термодинамической температурной шкалы. Экспериментально к этому можно приблизиться очень близко, но на самом деле не достичь, как это признается в третьем законе термодинамики . Было бы невозможно извлечь энергию в виде тепла из тела при такой температуре.

Температура важна во всех областях естествознания , включая физику , химию , науку о Земле , астрономию , медицину , биологию , экологию , материаловедение , металлургию , машиностроение и географию , а также в большинстве аспектов повседневной жизни.

Эффекты [ править ]

Многие физические процессы связаны с температурой; некоторые из них приведены ниже:

физические свойства материалов, включая фазу ( твердую , жидкую , газообразную или плазменную ), плотность , растворимость , давление паров , электропроводность , твердость , износостойкость , теплопроводность , коррозионную стойкость , прочность.
скорость и степень химических реакций протекания ^[1]
количество и свойства теплового излучения , испускаемого поверхностью объекта
температура воздуха влияет на все живые организмы
скорость звука , которая в газе пропорциональна квадратному корню из абсолютной температуры. ^[2]

Весы [ править ]

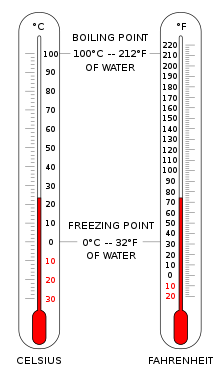
Для определения температурных шкал необходимы два значения: точка, выбранная за ноль градусов, и величина приращенной единицы температуры.

( Шкала Цельсия °C) используется для обычных измерений температуры в большинстве стран мира. Это эмпирическая шкала, которая сложилась исторически, в результате чего ее нулевая точка 0 ° C определяется как точка замерзания воды , а 100 ° C — как точка кипения воды, как при атмосферном давлении на уровне моря. Ее назвали стоградусной шкалой из-за интервала в 100 градусов. ^[3] После стандартизации кельвина в Международной системе единиц он впоследствии был переопределен с точки зрения эквивалентных точек фиксации по шкале Кельвина, так что приращение температуры на один градус Цельсия эквивалентно приращению на один кельвин, хотя численно шкалы различаются точным смещением 273,15.

широко Шкала Фаренгейта используется в Соединенных Штатах. Вода замерзает при температуре 32 °F и кипит при температуре 212 °F при атмосферном давлении на уровне моря.

Абсолютный ноль [ править ]

При абсолютном нуле температуры никакая энергия не может быть отведена от материи в виде тепла, и этот факт выражен в третьем законе термодинамики . При этой температуре вещество не содержит макроскопической тепловой энергии, но все же имеет квантовомеханическую нулевую энергию , как предсказывает принцип неопределенности , хотя это не входит в определение абсолютной температуры. Экспериментально к абсолютному нулю можно приблизиться лишь очень близко; она никогда не может быть достигнута (самая низкая температура, достигнутая экспериментом, составляет 38 пК). ^[4]Теоретически в теле при температуре абсолютного нуля прекращается всякое классическое движение его частиц и они находятся в полном покое в этом классическом смысле. Абсолютный ноль, определяемый как 0 K , в точности равен –273,15 °C или –459,67 °F .

Абсолютные шкалы [ править ]

Ссылаясь на константу Больцмана , распределение Максвелла – Больцмана Больцмана механическое определение энтропии и статистико - , в отличие от определения Гиббса, ^[5]для независимо движущихся микроскопических частиц, без учета межчастичной потенциальной энергии, по международному соглашению определяется температурная шкала, которая называется абсолютной, поскольку она не зависит от характеристик конкретных термометрических веществ и термометра механизмов . Кроме абсолютного нуля, у него нет эталонной температуры. Она известна как шкала Кельвина , широко используемая в науке и технике. Кельвин (название единицы пишется с маленькой буквы «к») — единица температуры в Международной системе единиц (СИ). Температура тела в состоянии термодинамического равновесия всегда положительна относительно абсолютного нуля.

Помимо международно признанной шкалы Кельвина, существует также термодинамическая температурная шкала , изобретенная лордом Кельвином , также с ее числовым нулем при абсолютном нуле температуры, но напрямую относящаяся к чисто макроскопическим термодинамическим концепциям, включая макроскопическую энтропию , хотя с микроскопической точки зрения ее можно отнести к Статистическое механическое определение Гиббса энтропии для канонического ансамбля , которое учитывает межчастичную потенциальную энергию, а также независимое движение частиц, так что оно может учитывать измерения температур, близких к абсолютному нулю. ^[5] Эта шкала имеет эталонную температуру в тройной точке воды, числовое значение которой определяется измерениями с использованием вышеупомянутой международно-согласованной шкалы Кельвина.

Шкала Кельвина [ править ]

Во многих научных измерениях используется температурная шкала Кельвина (обозначение единицы измерения: К), названная в честь физика, который первым ее определил . Это абсолютная шкала. Его числовая нулевая точка 0 К соответствует абсолютному нулю температуры. С мая 2019 года кельвин определяется с помощью кинетической теории частиц и статистической механики. В Международной системе единиц (СИ) величина кельвина определяется с помощью постоянной Больцмана , значение которой определяется как установленное международным соглашением. ^[6]^[7]

механические и температурные шкалы термодинамические Статистические

С мая 2019 года величина Кельвина определяется применительно к микроскопическим явлениям, характеризуемым с точки зрения статистической механики. Ранее, но с 1954 года, Международная система единиц определяла шкалу и единицу измерения кельвина как термодинамическую температуру , используя надежно воспроизводимую температуру тройной точки воды в качестве второй контрольной точки, причем первая контрольная точка составляла 0 К при абсолютный ноль. ^{[ нужна цитата ]}

Исторически температура тройной точки воды определялась как ровно 273,16 К. Сегодня это эмпирически измеряемая величина. Точка замерзания воды при атмосферном давлении на уровне моря происходит при температуре, очень близкой к 273,15 К ( 0 ° C ).

Классификация весов [ править ]

Существуют различные виды температурной шкалы. Возможно, будет удобно классифицировать их как эмпирически и теоретически обоснованные. Эмпирические температурные шкалы исторически старше, а теоретически обоснованные шкалы возникли в середине девятнадцатого века. ^[8]^[9]

Эмпирические шкалы [ править ]

Эмпирически обоснованные температурные шкалы основаны непосредственно на измерениях простых макроскопических физических свойств материалов. Например, длина столбика ртути, заключенного в капиллярной трубке со стеклянными стенками, во многом зависит от температуры и является основой очень полезного ртутного термометра в стекле. Такие шкалы действительны только в удобных диапазонах температур. Например, при температуре выше точки кипения ртути ртутный стеклянный термометр непригоден. Большинство материалов расширяются при повышении температуры, но некоторые материалы, такие как вода, сжимаются при повышении температуры в определенном диапазоне, и тогда их вряд ли можно использовать в качестве термометрических материалов. Материал бесполезен в качестве термометра вблизи одной из температур фазового перехода, например, точки кипения.

Несмотря на эти ограничения, наиболее часто используемые на практике термометры относятся к эмпирическому типу. В частности, его использовали для калориметрии , что внесло большой вклад в открытие термодинамики. Тем не менее, эмпирическая термометрия имеет серьезные недостатки, если рассматривать ее как основу теоретической физики. Термометры, основанные на эмпирическом опыте, помимо простых прямых измерений обычных физических свойств термометрических материалов, могут быть перекалиброваны с использованием теоретических физических рассуждений, и это может расширить диапазон их адекватности.

Теоретические шкалы

Теоретически обоснованные температурные шкалы основаны непосредственно на теоретических аргументах, особенно на аргументах кинетической теории и термодинамики. Они более или менее идеально реализованы в практически осуществимых физических устройствах и материалах. Теоретически обоснованные температурные шкалы используются в качестве калибровочных стандартов для практических термометров, основанных на эмпирическом опыте.

механическая шкала Микроскопическая статистическая

В физике принятая на международном уровне общепринятая шкала температур называется шкалой Кельвина. Он калибруется по согласованному и предписанному на международном уровне значению постоянной Больцмана, ^[6]^[7]Речь идет о движении микроскопических частиц, таких как атомы, молекулы и электроны, входящих в состав тела, температуру которого необходимо измерить. В отличие от термодинамической температурной шкалы, изобретенной Кельвином, общепринятая в настоящее время температура Кельвина не определяется ни путем сравнения с температурой эталонного состояния стандартного тела, ни с точки зрения макроскопической термодинамики.

Помимо абсолютного нуля температуры, температура Кельвина тела в состоянии внутреннего термодинамического равновесия определяется измерениями подходящим образом выбранных его физических свойств, которые имеют точное известное теоретическое объяснение в терминах постоянной Больцмана . ^{[ нужна цитата ]}Эта константа относится к избранным видам движения микроскопических частиц в составе тела. При таких видах движения частицы движутся индивидуально, без взаимного взаимодействия. Такие движения обычно прерываются столкновениями между частицами, но для измерения температуры движения выбираются так, чтобы между столкновениями неинтерактивные участки их траекторий были известны как доступные для точного измерения. При этом межчастичная потенциальная энергия не учитывается.

В идеальном газе и других теоретически понятных телах температура Кельвина определяется как пропорциональная средней кинетической энергии неинтерактивно движущихся микроскопических частиц, которую можно измерить подходящими методами. Константа пропорциональности представляет собой простое кратное константе Больцмана. Если молекулы, атомы или электроны ^[10]^[11] испускаются из материала и измеряются их скорости, спектр их скоростей часто почти подчиняется теоретическому закону, называемому распределением Максвелла-Больцмана , который дает обоснованное измерение температур, для которых этот закон выполняется. ^[12] Пока еще не было успешных экспериментов такого рода, которые напрямую использовали бы распределение Ферми–Дирака для термометрии, но, возможно, это будет достигнуто в будущем. ^[13]

характера газа Скорость звука в газе можно рассчитать теоретически, исходя из молекулярного , температуры, давления и постоянной Больцмана. Для газа с известным молекулярным характером и давлением это обеспечивает связь между температурой и постоянной Больцмана. Эти величины могут быть известны или измерены более точно, чем термодинамические переменные, определяющие состояние образца воды в его тройной точке. Следовательно, принимая значение постоянной Больцмана в качестве изначально определенного эталона точно определенного значения, измерение скорости звука может обеспечить более точное измерение температуры газа. ^[14]

Измерение спектра электромагнитного излучения идеального трехмерного черного тела может обеспечить точное измерение температуры, поскольку частота максимальной спектральной яркости излучения черного тела прямо пропорциональна температуре черного тела; это известно как закон смещения Вина и имеет теоретическое объяснение в законе Планка и законе Бозе-Эйнштейна .

Измерение спектра мощности шума, создаваемого электрическим резистором, также может обеспечить точное измерение температуры. Резистор имеет две клеммы и по сути представляет собой одномерное тело. Закон Бозе-Эйнштейна для этого случая показывает, что мощность шума прямо пропорциональна температуре резистора, значению его сопротивления и ширине полосы шума. В данной полосе частот мощность шума имеет равные вклады от каждой частоты и называется шумом Джонсона . Если известно значение сопротивления, то можно найти температуру. ^[15]^[16]

термодинамическая шкала Макроскопическая

Исторически сложилось так, что до мая 2019 года определение шкалы Кельвина было изобретенным Кельвином и основанным на соотношении количеств энергии в процессах в идеальном двигателе Карно, полностью с точки зрения макроскопической термодинамики. ^{[ нужна цитата ]}Этот двигатель Карно должен был работать между двумя температурами: температурой тела, температуру которого нужно было измерить, и эталонной температурой тела с температурой тройной точки воды. Тогда эталонная температура тройной точки была определена как равная ровно 273,16 К. С мая 2019 года это значение не зафиксировано по определению, но должно измеряться с помощью микроскопических явлений, включающих константу Больцмана, как описано выше. Микроскопическое статистическое механическое определение не имеет эталонной температуры.

Идеальный газ [ править ]

Материалом, на котором может быть основана макроскопически определенная температурная шкала, является идеальный газ . Давление, оказываемое фиксированным объемом и массой идеального газа, прямо пропорционально его температуре. Некоторые природные газы демонстрируют настолько почти идеальные свойства в подходящем диапазоне температур, что их можно использовать для термометрии; это было важно во время развития термодинамики и имеет практическое значение до сих пор. ^[17]^[18]Однако идеальный газовый термометр теоретически не идеален для термодинамики. Это связано с тем, что энтропия идеального газа при абсолютном нуле температуры не является положительной полуопределенной величиной, что ставит газ в нарушение третьего закона термодинамики. В отличие от реальных материалов, идеальный газ не сжижается и не затвердевает, каким бы холодным он ни был. Альтернативное мышление, закон идеального газа, относится к пределу бесконечно высокой температуры и нулевого давления; эти условия гарантируют невзаимодействующие движения составляющих молекул. ^[19]^[20]^[21]

кинетической Подход теории

Величина кельвина теперь определяется с точки зрения кинетической теории, полученной из значения постоянной Больцмана .

Кинетическая теория обеспечивает микроскопическое объяснение температуры некоторых тел материала, особенно газов, на основе того, что макроскопические системы состоят из множества микроскопических частиц, таких как молекулы и ионы различных видов, причем все частицы одного вида одинаковы. Он объясняет макроскопические явления посредством классической механики микроскопических частиц. Теорема о равнораспределении кинетической теории утверждает, что каждая классическая степень свободы свободно движущейся частицы имеет среднюю кинетическую энергию $k B T /2$ , где $k B$ обозначает постоянную Больцмана . ^{[ нужна цитата ]} Поступательное движение частицы имеет три степени свободы, так что, за исключением очень низких температур, когда преобладают квантовые эффекты, средняя поступательная кинетическая энергия свободно движущейся частицы в системе с температурой $Т$ будет равна $3 k B T /2$ .

Молекулы, такие как кислород (O ₂ ), имеют больше степеней свободы, чем отдельные сферические атомы: они совершают вращательные и колебательные движения, а также поступательные движения. Нагревание приводит к повышению температуры из-за увеличения средней поступательной кинетической энергии молекул. Нагревание также приведет к за счет эквираспределения увеличению энергии, связанной с колебательными и вращательными режимами, . Таким образом, двухатомному газу потребуется больше затрат энергии для повышения его температуры на определенную величину, т.е. он будет иметь большую теплоемкость , чем одноатомный газ.

Как отмечалось выше, скорость звука в газе можно рассчитать, исходя из молекулярного характера газа, температуры, давления и постоянной Больцмана. Принимая значение постоянной Больцмана в качестве первоначально определенного эталона точно определенного значения, измерение скорости звука может обеспечить более точное измерение температуры газа. ^[14]

Можно измерить среднюю кинетическую энергию составляющих микроскопических частиц, если им позволить выйти из объема системы через небольшое отверстие в содержащей стенке. Необходимо измерить спектр скоростей и на его основе рассчитать среднее значение. Это не обязательно тот случай, когда частицы, которые улетают и измеряются, имеют такое же распределение скоростей, как и частицы, которые остаются в объеме системы, но иногда возможен хороший образец.

Термодинамический подход [ править ]

Температура — одна из основных величин в изучении термодинамики . Раньше величина Кельвина определялась в терминах термодинамики, но в настоящее время, как упоминалось выше, она определяется в терминах кинетической теории.

Термодинамическую температуру называют абсолютной по двум причинам. Во-первых, его формальный характер не зависит от свойств конкретных материалов. Другая причина заключается в том, что его ноль в некотором смысле является абсолютным, поскольку он указывает на отсутствие микроскопического классического движения составляющих частиц материи, так что они имеют предельную нулевую удельную теплоемкость при нулевой температуре в соответствии с третьим законом. термодинамики. Тем не менее термодинамическая температура действительно имеет определенное числовое значение, произвольно выбранное по традиции и зависящее от свойств конкретных материалов; это просто менее произвольно, чем относительные шкалы «градусов», такие как Цельсия и Фаренгейта . Поскольку это абсолютная шкала с одной фиксированной точкой (нулем), для произвольного выбора остается только одна степень свободы, а не две, как в относительных шкалах. Для шкалы Кельвина с мая 2019 года международной конвенцией был сделан выбор в пользу использования знаний о режимах работы различных термометрических устройств, опирающихся на микроскопические кинетические теории молекулярного движения. Числовая шкала устанавливается общепринятым определением значения Константа Больцмана , которая связывает макроскопическую температуру со средней микроскопической кинетической энергией частиц, таких как молекулы. Его числовое значение произвольно, и существует альтернативная, менее широко используемая шкала абсолютных температур, называемая шкалой Ренкина , которая согласована со шкалой Фаренгейта, как Кельвин со шкалой Цельсия.

Термодинамическое определение температуры принадлежит Кельвину. Он создан в виде идеализированного устройства, называемого двигателем Карно , который, как предполагается, работает в воображаемом непрерывном цикле последовательных процессов , которые пересекают цикл состояний его рабочего тела. Двигатель забирает некоторое количество тепла $Q 1$ из горячего резервуара и отдает меньшее количество отходящего тепла $Q 2 < 0$ в холодный резервуар. Чистая тепловая энергия, поглощенная рабочим телом, передается в виде термодинамической работы в рабочий резервуар и считается мощностью двигателя. Предполагается, что цикл протекает настолько медленно, что в каждой точке цикла рабочее тело находится в состоянии термодинамического равновесия. Таким образом, предполагается, что последовательные процессы цикла протекают обратимо, без производства энтропии . Тогда количество энтропии, поступившей из горячего резервуара при нагреве рабочего тела, будет равно количеству энтропии, переданной в холодный резервуар при охлаждении рабочего тела. Тогда абсолютные или термодинамические температуры, $T 1$ и $T 2$ резервуаров определяются так, что ^[22]

{\frac {T_{1}}{T_{2}}}=-{\frac {Q_{1}}{Q_{2}}}.

(1)

Нулевой закон термодинамики позволяет использовать это определение для измерения абсолютной или термодинамической температуры произвольного интересующего тела, заставляя другой резервуар тепла иметь ту же температуру, что и интересующее тело.

Оригинальная работа Кельвина, постулирующая абсолютную температуру, была опубликована в 1848 году. Она была основана на работе Карно до формулировки первого закона термодинамики. У Карно не было ни четкого понимания тепла, ни конкретного понятия энтропии. Он написал о «калориях» и сказал, что все теплоты, прошедшие из горячего резервуара, перешли в холодный резервуар. Кельвин писал в своей статье 1848 года, что его шкала была абсолютной в том смысле, что она определялась «независимо от свойств какого-либо конкретного вида материи». Его окончательная публикация, в которой изложено только что изложенное определение, была напечатана в 1853 году, а статья прочитана в 1851 году. ^[23]^[24]^[25]^[26]

Численные детали ранее определялись путем создания одного из резервуаров тепла в виде ячейки в тройной точке воды, абсолютная температура которой была определена как 273,16 К. ^[27] В настоящее время числовое значение вместо этого получается путем измерения с помощью международного микроскопического статистического механического определения, как указано выше.

Интенсивная изменчивость

С термодинамической точки зрения температура является интенсивной переменной , поскольку она равна дифференциальному коэффициенту одной экстенсивной переменной по отношению к другой для данного тела. он имеет размеры отношения Таким образом , двух экстенсивных переменных. В термодинамике два тела часто рассматривают как соединенные контактом с общей стенкой, обладающей некоторыми специфическими проницаемыми свойствами. Такую удельную проницаемость можно отнести к конкретной интенсивной переменной. Примером может служить диатермическая стена, проницаемая только для тепла; интенсивной переменной в этом случае является температура. Когда два тела были соединены через специально проницаемую стенку в течение очень долгого времени и достигли постоянного устойчивого состояния, соответствующие интенсивные переменные равны в двух телах; для диатермической стенки это утверждение иногда называют нулевым законом термодинамики. ^[28]^[29]^[30]

В частности, когда тело описывается путем указания его внутренней энергии $U$ , экстенсивной переменной, как функции его энтропии $S$ , также экстенсивной переменной, и других переменных состояния $V, N$ , с $U = U (S, V, N$ ), то температура равна частной производной внутренней энергии по энтропии: ^[29]^[30]^[31]

T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}.

(2)

Аналогично, когда тело описывается путем указания его энтропии $S$ как функции его внутренней энергии $U$ и других переменных состояния $V, N$ с $S = S (U, V, N)$ , тогда обратная величина температуры равна частная производная энтропии по внутренней энергии: ^[29]^[31]^[32]

{\frac {1}{T}}=\left({\frac {\partial S}{\partial U}}\right)_{V,N}.

(3)

Приведенное выше определение абсолютной температуры, уравнение (1), дано Кельвину. Оно относится к системам, закрытым для переноса вещества, и уделяет особое внимание непосредственно экспериментальным процедурам. Изложение термодинамики Гиббсом начинается на более абстрактном уровне и касается систем, открытых для переноса материи; в этом развитии термодинамики приведенные выше уравнения (2) и (3) фактически являются альтернативными определениями температуры. ^[33]

термодинамическое равновесие Локальное

Реальные тела часто не находятся в термодинамическом равновесии и не однородны. Для исследования методами классической необратимой термодинамики тело обычно концептуально разделяют в пространстве и времени на «ячейки» небольшого размера. Если в такой «ячейке» с хорошим приближением выполняются классические условия термодинамического равновесия вещества, то она однородна и для нее существует температура. Если это так для каждой «клетки» тела, то говорят, что локальное термодинамическое равновесие преобладает во всем теле. ^[34]^[35]^[36]^[37]^[38]

Имеет смысл, например, сказать об экстенсивной переменной $U$ или об экстенсивной переменной $S$ , что она имеет плотность на единицу объема или количество на единицу массы системы, но бессмысленно говорить об экстенсивной переменной S . плотность температуры на единицу объема или количество температуры на единицу массы системы. С другой стороны, нет смысла говорить о внутренней энергии в точке, а при преобладании локального термодинамического равновесия имеет смысл говорить о температуре в точке. Следовательно, температура может меняться от точки к точке в среде, не находящейся в глобальном термодинамическом равновесии, но в которой существует локальное термодинамическое равновесие.

Таким образом, когда в теле преобладает локальное термодинамическое равновесие, температуру можно рассматривать как пространственно изменяющееся локальное свойство этого тела, поскольку температура является интенсивной переменной.

Основная теория [ править ]

Температура является мерой качества состояния материала. ^[39] Качество можно рассматривать как более абстрактную сущность, чем любая конкретная температурная шкала, которая его измеряет, и называют его жаром . некоторые авторы ^[40]^[41]^[42]Качество теплоты относится к состоянию материала только в определенной местности, и вообще, за исключением тел, находящихся в устойчивом состоянии термодинамического равновесия, жара варьируется от места к месту. Это не обязательно тот случай, когда материал в определенном месте находится в устойчивом и почти однородном состоянии, позволяющем ему иметь четко определенную температуру или температуру. Теплоту можно абстрактно представить как одномерное многообразие . Каждая действующая температурная шкала имеет свою собственную карту в многообразии температуры. ^[43]^[44]

Когда две системы, находящиеся в тепловом контакте, имеют одинаковую температуру, теплообмен между ними отсутствует. Когда существует разница температур, тепло самопроизвольно перетекает от более теплой системы к более холодной, пока они не придут в тепловое равновесие . Такая передача тепла происходит за счет проводимости или теплового излучения. ^[45]^[46]^[47]^[48]^[49]^[50]^[51]^[52]

Физики-экспериментаторы, например Галилей и Ньютон , ^[53]обнаружил, что существует бесконечно много эмпирических температурных шкал . Тем не менее, нулевой закон термодинамики гласит, что все они измеряют одно и то же качество. Это значит, что для тела, находящегося в состоянии внутреннего термодинамического равновесия, всякий правильно откалиброванный термометр любого типа, измеряющий температуру тела, регистрирует одну и ту же температуру. Для тела, не находящегося в состоянии внутреннего термодинамического равновесия, разные термометры могут регистрировать разные температуры в зависимости соответственно от механизмов действия термометров.

Тела в термодинамическом равновесии [ править ]

Для экспериментальной физики тепло означает, что при сравнении любых двух данных тел в их соответствующих отдельных термодинамических состояниях любые два эмпирических термометра с показаниями числовой шкалы согласуются относительно того, какое из двух данных тел более горячее, или что они имеют та же температура. ^[54] Это не требует, чтобы два термометра имели линейную зависимость между показаниями их числовых шкал, но требует, чтобы связь между их числовыми показаниями была строго монотонной . ^[55]^[56]Определенное ощущение большей температуры, независимо от калориметрии, термодинамики и свойств конкретных материалов, можно получить закона смещения Вина теплового излучения : температура ванны теплового излучения пропорциональна из универсальной константе частота максимума его частотного спектра ; эта частота всегда положительна, но может иметь значения, стремящиеся к нулю . Тепловое излучение первоначально определяется для полости, находящейся в термодинамическом равновесии. Эти физические факты оправдывают математическое утверждение о том, что тепло существует в упорядоченном одномерном многообразии . Это фундаментальный признак температуры и термометров для тел, находящихся в собственном термодинамическом равновесии. ^[8]^[43]^[44]^[57]^[58]

За исключением системы, претерпевающей первого порядка фазовый переход , такой как таяние льда, по мере того, как замкнутая система получает тепло, без изменения ее объема и без изменения действующих на нее внешних силовых полей ее температура повышается. Для системы, претерпевающей такой фазовый переход настолько медленно, что отклонением от термодинамического равновесия можно пренебречь, ее температура остается постоянной, поскольку в систему поступает скрытое тепло . И наоборот, потеря тепла из закрытой системы без фазового перехода, без изменения объема и без изменения внешних силовых полей, действующих на нее, снижает ее температуру. ^[59]

Тела, находящиеся в устойчивом состоянии, но не в термодинамическом равновесии [ править ]

В то время как для тел, находящихся в их собственных состояниях термодинамического равновесия, понятие температуры требует, чтобы все эмпирические термометры соглашались относительно того, какое из двух тел горячее или что они имеют одинаковую температуру, это требование небезопасно для тел, находящихся в устойчивом состоянии. состояния, хотя и не находящиеся в термодинамическом равновесии. Тогда вполне может быть, что разные эмпирические термометры расходятся во мнениях относительно того, какой из них горячее, и если это так, то по крайней мере одно из тел не имеет четко определенной абсолютной термодинамической температуры. Тем не менее, любое данное тело и любой подходящий эмпирический термометр все же могут поддерживать понятия эмпирической, неабсолютной теплоты и температуры для подходящего диапазона процессов. Это предмет изучения неравновесной термодинамики . ^{[ нужна цитата ]}

Тела не находятся в устойчивом состоянии [ править ]

Когда тело не находится в устойчивом состоянии, понятие температуры становится еще менее безопасным, чем для тела, находящегося в устойчивом состоянии и не находящегося в термодинамическом равновесии. Это также является предметом изучения неравновесной термодинамики .

равновесия Аксиоматика термодинамического

Для аксиоматической трактовки термодинамического равновесия с 1930-х годов стало принято ссылаться на нулевой закон термодинамики . Обычно формулируемая минималистская версия такого закона постулирует только то, что все тела, которые при термическом соединении находились бы в тепловом равновесии, должны иметь одинаковую температуру по определению, но сама по себе не устанавливает температуру как величину, выраженную как действительная величина. число на шкале. Более физически информативная версия такого закона рассматривает эмпирическую температуру как диаграмму на многообразии температуры. ^[43]^[58]^[60] В то время как нулевой закон допускает определения многих различных эмпирических шкал температуры, второй закон термодинамики выбирает определение одной предпочтительной абсолютной температуры , уникальной с точностью до произвольного масштабного коэффициента, откуда она называется термодинамической температурой . ^[8]^[43]^[61]^[62]^[63]^[64]Если внутреннюю энергию рассматривать как функцию объема и энтропии однородной системы, находящейся в термодинамическом равновесии, термодинамическая абсолютная температура появляется как частная производная внутренней энергии по энтропии при постоянном объеме. Его естественным, внутренним источником или нулевой точкой является абсолютный ноль, при котором энтропия любой системы минимальна. Хотя это самая низкая абсолютная температура, описываемая моделью, третий закон термодинамики постулирует, что абсолютный ноль не может быть достигнут ни одной физической системой.

Теплоемкость [ править ]

Когда передача энергии к телу или от него осуществляется только в виде тепла, состояние тела меняется. В зависимости от окружающей среды и стен, отделяющих их от тела, в организме возможны различные изменения. Они включают химические реакции, повышение давления, повышение температуры и фазовый переход. Для каждого вида изменения при определенных условиях теплоемкость представляет собой отношение количества переданного тепла к величине изменения. ^[65]

Например, если изменение представляет собой повышение температуры при постоянном объеме, без фазового перехода и без химического изменения, то температура тела повышается и его давление увеличивается. Количество переданного тепла $Δ Q$ , разделенное на наблюдаемое изменение температуры $Δ T$ тела , представляет собой теплоемкость при постоянном объеме:

C_{V}={\frac {\Delta Q}{\Delta T}}.

Если теплоемкость измеряется для четко определенного количества вещества , удельная теплота является мерой тепла, необходимого для увеличения температуры такой единицы количества на одну единицу температуры. Например, для повышения температуры воды на один кельвин (равный одному градусу Цельсия) требуется 4186 джоулей на килограмм (Дж/кг).

Измерение [ править ]

Типичный термометр Цельсия измеряет зимнюю дневную температуру -17 ° C.

Измерение температуры с использованием современных научных термометров и температурных шкал восходит, по крайней мере, к началу 18 века, когда Даниэль Габриэль Фаренгейт адаптировал термометр (переход на ртуть ) и шкалу, разработанные Оле Кристенсеном Рёмером . Шкала Фаренгейта до сих пор используется в США в ненаучных целях.

Температуру измеряют термометрами , которые можно калибровать по различным температурным шкалам . В большинстве стран мира (за исключением Белиза , Мьянмы , Либерии и США ) шкала Цельсия используется для большинства целей измерения температуры. Большинство учёных измеряют температуру по шкале Цельсия, а термодинамическую температуру — по шкале Кельвина , которая представляет собой смещение шкалы Цельсия, так что её нулевая точка равна 0 K = −273,15 °C , или абсолютному нулю . Многие инженерные области в США, особенно высокие технологии и федеральные спецификации США (гражданские и военные), также используют шкалы Кельвина и Цельсия. Другие инженерные области в США также полагаются на шкалу Рэнкина (сдвинутая шкала Фаренгейта) при работе в термодинамических дисциплинах, таких как горение .

Единицы [ править ]

Основной единицей температуры в Международной системе единиц (СИ) является кельвин . Имеет символ К.

Для повседневного применения часто удобно использовать шкалу Цельсия, в которой 0 °C очень близко соответствует температуре замерзания воды, а 100 °C — температуре ее кипения на уровне моря. Поскольку капли жидкости обычно существуют в облаках при минусовых температурах, 0 °C лучше определить как точку плавления льда. В этой шкале разница температур в 1 градус Цельсия равна приращению в 1 Кельвин , но масштаб компенсируется температурой, при которой тает лед ( 273,15 К ).

По международному соглашению, ^[66]до мая 2019 года шкалы Кельвина и Цельсия определялись двумя точками фиксации: абсолютным нулем и тройной точкой Венского стандарта средней океанской воды , которая представляет собой воду, специально приготовленную с определенной смесью изотопов водорода и кислорода. Абсолютный ноль определялся как ровно 0 К и -273,15 °С . Это температура, при которой все классические поступательные движения частиц, составляющих материю, прекращаются и они находятся в полном покое в классической модели. Однако с квантовой точки зрения движение нулевой точки сохраняется и имеет связанную с ней энергию, энергию нулевой точки . Материя находится в своем основном состоянии , ^[67]и не содержит тепловой энергии . Температуры 273,16 К и 0,01 °С были определены как температуры тройной точки воды. Это определение преследовало следующие цели: оно фиксировало величину кельвина как равную ровно 1 части из 273,16 частей разницы между абсолютным нулем и тройной точкой воды; было установлено, что один кельвин имеет точно такую же величину, как один градус по шкале Цельсия; и установило, что разница между нулевыми точками этих шкал равна 273,15 К ( 0 К = -273,15 °С и 273,16 К = 0,01 °С ). С 2019 года появилось новое определение, основанное на постоянной Больцмана: ^[68] но масштабы почти не изменились.

В США наиболее широко используется шкала Фаренгейта. По этой шкале точка замерзания воды соответствует 32 °F , а точка кипения — 212 °F . Шкала Ренкина, до сих пор используемая в области химического машиностроения в США, представляет собой абсолютную шкалу, основанную на приращении по Фаренгейту.

Исторические шкалы [ править ]

Следующие температурные шкалы используются или исторически использовались для измерения температуры:

Физика плазмы [ править ]

Область физики плазмы занимается явлениями электромагнитной природы, связанными с очень высокими температурами. Принято выражать температуру как энергию в единицах, связанных с или килоэлектронвольтом ( эВ/ кВ _{электронвольтом} / кВ _{или кэВ} ). Соответствующая энергия, которая по размерам отличается от температуры, затем рассчитывается как произведение постоянной Больцмана и температуры: $E=k_{\text{B}}T$ . Тогда / кВ _{составляет} 11 605 К. эВ 1 При изучении вещества КХД обычно встречаются температуры порядка нескольких сотен МэВ/ кВ _{, что} эквивалентно примерно 10 ¹² К.

Непрерывный или дискретный [ править ]

Когда измеряют изменение температуры в определенной области пространства или времени, оказываются ли измерения температуры непрерывными или дискретными? Существует широко распространенное заблуждение, что такие измерения температуры всегда должны быть непрерывными. ^[69] Это заблуждение частично происходит из исторической точки зрения, связанной с непрерывностью классических физических величин , которая утверждает, что физические величины должны принимать каждое промежуточное значение между начальным значением и конечным значением. ^[69]^[70] Однако классическая картина справедлива только в тех случаях, когда температура измеряется в системе, находящейся в равновесии , то есть вне этих условий температура не может быть непрерывной. ^[69] Для систем, находящихся вне равновесия, например, на границах раздела материалов (например, граница раздела металл/неметалл или граница раздела жидкость-пар), измерения температуры могут показывать резкие разрывы во времени и пространстве. ^[69] Например, Фанг и Уорд были одними из первых авторов, которые успешно сообщили о скачках температуры до 7,8 К на поверхности испаряющихся капель воды. ^[71] Об этом сообщалось в межмолекулярном масштабе или в масштабе длины свободного пробега молекул, которая обычно составляет порядка нескольких микрометров в газах. ^[72]при комнатной температуре. Вообще говоря, в случаях межфазной теплопередачи скачки температуры считаются нормой, а не исключением. ^[73] Это происходит из-за резкого изменения вибрационных или тепловых свойств материалов на таких границах раздела, что предотвращает мгновенную передачу тепла и установление теплового равновесия (необходимое условие для наличия однородной равновесной температуры на границе раздела). ^[74]^[75] Кроме того, измерения температуры на макромасштабе (типичный масштаб наблюдений) могут быть слишком грубыми, поскольку они усредняют микроскопическую тепловую информацию на основе масштаба репрезентативного объема выборки системы управления, и, таким образом, вполне вероятно, что температурные скачки в микромасштабе могут быть упущены из виду в таких средних показателях. ^[69] Такое усреднение может даже давать неправильные или вводящие в заблуждение результаты во многих случаях измерения температуры, даже на макромасштабе, и поэтому разумно тщательно изучить микрофизическую информацию, прежде чем усреднять или сглаживать любые потенциальные температурные скачки в системе. поскольку такие разрывы не всегда можно усреднить или сгладить. ^[69]^[76] Температурные неравномерности, а не просто аномалии, на самом деле существенно улучшили наше понимание и возможности прогнозирования, касающиеся теплопередачи в небольших масштабах. ^[69]^[73]^[74]^[75]^[76]

Теоретическая основа [ править ]

Исторически сложилось так, что существует несколько научных подходов к объяснению температуры: классическое термодинамическое описание, основанное на макроскопических эмпирических переменных, которые можно измерить в лаборатории; кинетическая теория газов , связывающая макроскопическое описание с вероятностным распределением энергии движения частиц газа; и микроскопическое объяснение, основанное на статистической физике и квантовой механике . Кроме того, строгие и чисто математические подходы обеспечили аксиоматический подход к классической термодинамике и температуре. ^[77]Статистическая физика обеспечивает более глубокое понимание, описывая атомное поведение материи и выводит макроскопические свойства из статистических средних значений микроскопических состояний, включая как классические, так и квантовые состояния. В фундаментальном физическом описании температура может быть измерена непосредственно в единицах энергии. Однако в практических системах измерения науки, техники и торговли, таких как современная метрическая система единиц, макроскопические и микроскопические описания взаимосвязаны константой Больцмана , коэффициентом пропорциональности, который масштабирует температуру до микроскопической средней кинетической энергии. .

Микроскопическое описание в статистической механике основано на модели, которая анализирует систему на ее фундаментальные частицы материи или на набор классических или -механических осцилляторов и рассматривает систему как статистический ансамбль микросостояний квантово . Как совокупность классических материальных частиц, температура является мерой средней энергии движения, называемой поступательной кинетической энергией частиц, будь то в твердых телах, жидкостях, газах или плазме. Кинетическая энергия, концепция классической механики , равна половине массы частицы, умноженной на квадрат ее скорости . В этой механической интерпретации теплового движения кинетическая энергия материальных частиц может заключаться в скорости частиц их поступательного или колебательного движения или в инерции их вращательных мод. В одноатомных совершенных газах и, примерно, в большинстве газов и в простых металлах, температура является мерой средней поступательной кинетической энергии частицы, 3/2 k _B T . Он также определяет функцию распределения вероятностей энергии. В конденсированном состоянии, и особенно в твердых телах, это чисто механическое описание часто менее полезно, и модель осциллятора обеспечивает лучшее описание для объяснения квантово-механических явлений. Температура определяет статистическую заселенность микросостояний ансамбля. Микроскопическое определение температуры имеет смысл только в термодинамический предел , означающий для больших ансамблей состояний или частиц, отвечающий требованиям статистической модели.

Кинетическая энергия также рассматривается как составная часть тепловой энергии . Тепловую энергию можно разделить на независимые компоненты, связанные со степенями свободы частиц или режимами осцилляторов в термодинамической системе . Вообще число этих степеней свободы, доступных для экраспределения энергии, зависит от температуры, т. е. от энергетической области рассматриваемых взаимодействий. Для твердых тел тепловая энергия связана прежде всего с колебаниями его атомов или молекул около положения равновесия. В идеальном одноатомном газе кинетическая энергия обнаруживается исключительно в чисто поступательном движении частиц. В других системах вибрационные и вращательные движения также вносят степени свободы.

Кинетическая теория газов [ править ]

Максвелл и Больцман разработали кинетическую теорию , которая дает фундаментальное понимание температуры в газах. ^[78] Эта теория также объясняет закон идеального газа и наблюдаемую теплоемкость одноатомных (или «благородных» ) газов. ^[79]^[80]^[81]

Закон идеального газа основан на наблюдаемых эмпирических отношениях между давлением ( p ), объемом ( V ) и температурой ( T ) и был признан задолго до того, как была разработана кинетическая теория газов (см. Бойля и Чарльза законы ). Закон идеального газа гласит: ^[82]

pV=nRT,

где n — количество молей газа, а R = 8,314 462 618 …Дж⋅моль. ⁻¹⋅K ⁻¹^[83] это газовая постоянная .

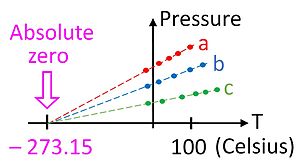
Это соотношение дает нам первый намек на то, что на шкале температур существует абсолютный ноль , потому что он справедлив только в том случае, если температура измеряется по абсолютной шкале, такой как шкала Кельвина. Закон идеального газа позволяет измерять температуру в этой абсолютной шкале с помощью газового термометра . Температуру в кельвинах можно определить как давление в паскалях одного моля газа в сосуде объемом один кубический метр, разделенное на газовую постоянную.

Хотя это не особенно удобное устройство, газовый термометр обеспечивает важную теоретическую основу, с помощью которой можно калибровать все термометры. На практике невозможно использовать газовый термометр для измерения абсолютной нулевой температуры, поскольку газы конденсируются в жидкость задолго до того, как температура достигнет нуля. Однако можно экстраполировать до абсолютного нуля, используя закон идеального газа, как показано на рисунке.

Кинетическая теория предполагает, что давление вызвано силой, связанной с ударами отдельных атомов о стенки, и что вся энергия представляет собой поступательную кинетическую энергию . Используя сложный аргумент симметрии, ^[84] Больцман вывел то, что сейчас называется функцией распределения вероятностей Максвелла – Больцмана для скорости частиц в идеальном газе. Из этой функции распределения вероятностей средняя кинетическая энергия (на частицу) одноатомного идеального газа равна ^[80]^[85]

E_{\text{k}}={\frac {1}{2}}mv_{\text{rms}}^{2}={\frac {3}{2}}k_{\text{B}}T,

где постоянная Больцмана k _B — постоянная идеального газа, деленная на число Авогадро , и ${\textstyle v_{\text{rms}}={\sqrt {\langle v^{2}\rangle }}={\sqrt {\langle \mathbf {v\cdot v} \rangle }}}$ — среднеквадратическая скорость . ^[86]Эта прямая пропорциональность между температурой и средней молекулярной кинетической энергией является частным случаем теоремы о равнораспределении и справедлива только в классическом пределе идеального газа . Это не справедливо для большинства веществ.

Нулевой закон термодинамики [ править ]

Когда два изолированных тела соединяются вместе жестким физическим путем, непроницаемым для материи, происходит самопроизвольная передача энергии в виде тепла от более горячего к более холодному из них. В конце концов, они достигают состояния взаимного теплового равновесия , в котором теплопередача прекращается, а соответствующие переменные состояния тел становятся неизменными. ^[87]^[88]^[89]

Одно из утверждений нулевого закона термодинамики заключается в том, что если каждая из двух систем находится в тепловом равновесии с третьей системой, то они также находятся в тепловом равновесии друг с другом. ^[90]^[91]^[92]

Это утверждение помогает определить температуру, но само по себе оно не завершает определение. Эмпирическая температура — это числовая шкала температуры термодинамической системы. Такую теплоту можно определить как существующую в одномерном многообразии , простирающемся между горячим и холодным. Иногда утверждается, что нулевой закон включает существование уникального универсального многообразия температуры и числовых шкал на нем, чтобы обеспечить полное определение эмпирической температуры. ^[60]Чтобы быть пригодным для эмпирической термометрии, материал должен иметь монотонную связь между теплотой и некоторой легко измеряемой переменной состояния, такой как давление или объем, когда все другие соответствующие координаты фиксированы. Исключительно подходящей системой является идеальный газ , который может обеспечить шкалу температур, соответствующую абсолютной шкале Кельвина. Шкала Кельвина определяется на основе второго закона термодинамики.

Второй закон термодинамики [ править ]

В качестве альтернативы рассмотрению или определению нулевого закона термодинамики историческим развитием термодинамики было определение температуры в терминах второго закона термодинамики, который касается энтропии . ^{[ нужна цитата ]}Второй закон гласит, что любой процесс приведет либо к отсутствию изменений, либо к чистому увеличению энтропии Вселенной. Это можно понять с точки зрения вероятности.

Например, в серии подбрасываний монеты идеально упорядоченной системой будет та, в которой либо при каждом подбрасывании выпадает орел, либо при каждом подбрасывании выпадает решка. Это означает, что результат всегда на 100% один и тот же. Напротив, многие смешанные ( неупорядоченные возможны ) исходы, и их количество увеличивается с каждым броском. В конце концов, комбинации ~50% орла и ~50% решки доминируют, и получение результата, значительно отличающегося от 50/50, становится все более маловероятным. Таким образом, система естественным образом переходит в состояние максимального беспорядка или энтропии.

Поскольку температура управляет передачей тепла между двумя системами, а Вселенная стремится к максимуму энтропии, ожидается, что существует некоторая связь между температурой и энтропией. Тепловая машина – это устройство для преобразования тепловой энергии в механическую, в результате чего совершается работа. Анализ тепловой машины Карно дает необходимые соотношения. Согласно закону сохранения энергии, поскольку энергия является функцией состояния , которая не изменяется в течение полного цикла, работа тепловой машины за полный цикл равна чистой теплоте, т. е. сумме тепла, переданной в систему при высокой температуре, q _H > 0, а отходящее тепло, выделяемое при низкой температуре, q _C < 0. ^[93]

КПД равен работе, деленной на погонную теплоту:

{\text{efficiency}}={\frac {w_{\text{cy}}}{q_{\text{H}}}}={\frac {q_{\text{H}}+q_{\text{C}}}{q_{\text{H}}}}=1-{\frac {|q_{\text{C}}|}{q_{\text{H}}}},

(4)

где w _cy — работа, совершаемая за цикл. Эффективность зависит только от | q _C |/ q _ЧАС . Поскольку q _C и q _H соответствуют теплообмену при температурах и _TC TH соответственно _| , q _C |/ q _H должно быть некоторой функцией этих температур:

{\frac {|q_{\text{C}}|}{q_{\text{H}}}}=f\left(T_{\text{H}},T_{\text{C}}\right).

(5)

Теорема Карно утверждает, что все обратимые двигатели, работающие с одними и теми же тепловыми резервуарами, одинаково эффективны. ^{[ нужна цитата ]}Таким образом, тепловая машина, работающая между Т ₁ и Т _{3 ,} должна иметь такой же КПД, как и машина, состоящая из двух циклов, один между Т ₁ и Т ₂ , а второй между Т ₂ и Т ₃ . Это может быть только в том случае, если

q_{13}={\frac {q_{1}q_{2}}{q_{2}q_{3}}},

что подразумевает

q_{13}=f\left(T_{1},T_{3}\right)=f\left(T_{1},T_{2}\right)f\left(T_{2},T_{3}\right).

Поскольку первая функция не зависит от T ₂ , эта температура должна сокращаться в правой части, что означает, что f ( T ₁ , T ₃ ) имеет форму g ( T ₁ )/ g ( T ₃ ) (т.е. f ( T ₁ , T 3 ) Т ₃ ) знак равно ж ( Т ₁ , Т ₂ ) ж ( Т ₂ , Т ₃ ) знак равно г ( Т ₁ ) / г ( Т ₂ ) · г ( Т ₂ ) / г ( Т ₃ ) знак равно г ( Т ₁ ) / g ( T ₃ )) , где g — функция одной температуры. Теперь можно выбрать температурную шкалу с учетом того свойства, что

{\frac {|q_{\text{C}}|}{q_{\text{H}}}}={\frac {T_{\text{C}}}{T_{\text{H}}}}.

(6)

Подстановка (6) обратно в (4) дает зависимость эффективности от температуры:

{\text{efficiency}}=1-{\frac {|q_{\text{C}}|}{q_{\text{H}}}}=1-{\frac {T_{\text{C}}}{T_{\text{H}}}}.

(7)

Для TC _К = 0 К эффективность составляет 100 %, и эта эффективность становится больше 100 % ниже 0 К. Поскольку эффективность, превышающая 100 %, нарушает первый закон термодинамики, это означает, что 0 — это минимально возможная температура. Фактически, самая низкая температура, когда-либо полученная в макроскопической системе , составила 20 нК и была достигнута в 1995 году в НИСТ. Вычитание правой части (5) из средней части и перестановка дает ^[22]^[93]

{\frac {q_{\text{H}}}{T_{\text{H}}}}+{\frac {q_{\text{C}}}{T_{\text{C}}}}=0,

где отрицательный знак указывает на тепло, выделяемое из системы. Это соотношение предполагает существование функции состояния S , изменение которой обычно исчезает для полного цикла, если она определяется формулой

dS={\frac {dq_{\text{rev}}}{T}},

(8)

где нижний индекс указывает на обратимый процесс. Эта функция соответствует энтропии системы, которая была описана ранее. Перестановка (8) дает формулу для температуры через фиктивные бесконечно малые квазиобратимые элементы энтропии и тепла:

T={\frac {dq_{\text{rev}}}{dS}}.

(9)

Для системы постоянного объема, где энтропия S ( E ) является функцией ее энергии E , d E = d q _rev и (9) дает

T^{-1}={\frac {d}{dE}}S(E),

(10)

т.е. обратная температура - это скорость увеличения энтропии по отношению к энергии при постоянном объеме.

статистической механики Определение из

Статистическая механика определяет температуру на основе фундаментальных степеней свободы системы. Уравнение (10) является определяющим соотношением температуры, где энтропия $S$ определяется (с точностью до константы) логарифмом числа микросостояний системы в данном макросостоянии (как указано в микроканоническом ансамбле ):

S=k_{\mathrm {B} }\ln(W)

где $k_{\mathrm {B} }$ – постоянная Больцмана, W – число микросостояний с энергией E системы (вырождение).

Когда две системы с разными температурами соединяются чисто термически, тепло перетекает от системы с более высокой температурой к системе с более низкой температурой; термодинамически это понимается под вторым законом термодинамики: общее изменение энтропии после передачи энергии $\Delta E$ из системы 1 в систему 2:

\Delta S=-(dS/dE)_{1}\cdot \Delta E+(dS/dE)_{2}\cdot \Delta E=\left({\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}\right)\Delta E

и поэтому положителен, если $T_{1}>T_{2}$

С точки зрения статистической механики общее число микросостояний в объединенной системе 1 + система 2 равно $N_{1}\cdot N_{2}$ , логарифм которого (умноженный на константу Больцмана) представляет собой сумму их энтропий; таким образом, поток тепла от высокой температуры к низкой, приводящий к увеличению общей энтропии, более вероятен, чем любой другой сценарий (обычно он гораздо более вероятен), поскольку в результирующем макросостоянии больше микросостояний.

отдельных частиц из статистики Обобщенная температура

Определение температуры можно распространить даже на системы из нескольких частиц, например, на квантовую точку . Обобщенная температура получается путем рассмотрения временных ансамблей вместо ансамблей конфигурационного пространства, заданных в статистической механике, в случае теплового обмена и обмена частицами между небольшой системой фермионов ( N даже менее 10) с одно-/двухзаселенной системой. Конечный квантовый великий канонический ансамбль ^[94] полученные в рамках гипотезы эргодичности и ортодичности, ^[95] позволяет выразить обобщенную температуру из отношения среднего времени пребывания $\tau _{1}$ и $\tau _{2}$ одноместной/двухместной системы: ^[96]

T={\frac {E-E_{\text{F}}\left(1+{\frac {3}{2N}}\right)}{k_{\text{B}}\ln \left(2{\frac {\tau _{2}}{\tau _{1}}}\right)}},

где E _F — энергия Ферми . Эта обобщенная температура стремится к обычной температуре, когда N стремится к бесконечности.

Отрицательная температура [ править ]

В эмпирических температурных шкалах, не привязанных к абсолютному нулю, отрицательная температура — это температура ниже нулевой точки используемой шкалы. Например, сухой лед имеет температуру сублимации -78,5 °C , что эквивалентно -109,3 °F . ^[97]По абсолютной шкале Кельвина эта температура составляет 194,6 К. Ни одно тело не может быть доведено точно до 0 К (температура идеально самого холодного тела) с помощью любого конечного практически осуществимого процесса; это следствие третьего закона термодинамики . ^[98]^[99]^[100]

Внутренняя кинетическая теория температуры тела не может принимать отрицательные значения. Однако термодинамическая температурная шкала не так ограничена.

Для тела материи иногда можно концептуально определить, с точки зрения микроскопических степеней свободы, а именно спины частиц, подсистему с температурой, отличной от температуры всего тела. Когда тело находится в состоянии внутреннего термодинамического равновесия, температуры всего тела и подсистемы должны быть одинаковыми. Две температуры могут различаться, когда посредством работы через внешние силовые поля энергия может передаваться в подсистему и обратно отдельно от остальной части тела; тогда все тело не находится в состоянии внутреннего термодинамического равновесия. Существует верхний предел энергии, которого может достичь такая спиновая подсистема.

Считая подсистему находящейся во временном состоянии виртуального термодинамического равновесия, можно получить отрицательную температуру по термодинамической шкале. Термодинамическая температура является обратной производной энтропии подсистемы по ее внутренней энергии. По мере увеличения внутренней энергии подсистемы энтропия увеличивается в некотором диапазоне, но в конечном итоге достигает максимального значения, а затем начинает уменьшаться по мере того, как начинают заполняться состояния с наивысшей энергией. В точке максимума энтропии температурная функция демонстрирует поведение сингулярности , поскольку наклон энтропии как функции энергии уменьшается до нуля, а затем становится отрицательным. Когда энтропия подсистемы достигает максимума, ее термодинамическая температура достигает положительной бесконечности, переходя на отрицательную бесконечность, когда наклон становится отрицательным. Такие отрицательные температуры жарче, чем любая положительная температура. Со временем, когда подсистема подвергается воздействию остальной части тела, имеющей положительную температуру, энергия передается в виде тепла от подсистемы с отрицательной температурой к системе с положительной температурой. ^[101] Температура кинетической теории для таких подсистем не определена.

Примеры [ править ]

Сравнение температур в различных масштабах
	Температура		Пиковая длина волны эмиттанса ^[а] излучения черного тела
	Кельвин	Цельсия	Пиковая длина волны эмиттанса ^[а] излучения черного тела
Абсолютный ноль (точно по определению)	0 К	−273,15 °С	Бесконечность
Температура черного тела черной дыры центр нашей галактики, Стрелец А* ^[103]	15 ФК	−273,149 999 999 999 985 °С	2.5 × 10 ⁸ км ( 1,7 а.е. )
Самая низкая температура достигнуто ^[104]	100 пк	−273,149 999 999 900 °С	29 000 км
Самый холодный Конденсат Бозе – Эйнштейна ^[б]	450 пк	−273,149 999 999 55 °С	6400 км
Один милликельвин (точно по определению)	0,001 К	−273,149 ° С	2.897 77 м (радио, FM-диапазон ) ^[с]
Космический микроволновый фон (измерение 2013 г.)	2,7260 К	−270,424 ° С	0,001 063 01 м (микроволновая печь миллиметрового диапазона)
воды Тройная точка (ранее по определению) ^[д]	273,16 К	0,01 °С	10 608,3 морских миль (длинноволновой ИК )
воды Температура кипения ^[А]	373,1339 К	99,9839 °С	7 766,03 морских миль (средневолновой ИК)
железа Температура плавления	1811 К	1538 °С	1600 нм ( дальний инфракрасный )
Лампа накаливания ^[Б]	2500 К	≈ 2200 °С	1160 нм (ближний инфракрасный ) ^[С]
Солнца Видимая поверхность ^[Д]^[Это]	5778 К	5505 °С	501,5 нм ( зелено-синий свет )
Удар молнии канал ^[И]	28 кК	28 000 °С	100 нм (дальний ультрафиолет )
Ядро Солнца ^[И]	16 МК	16 миллионов °С	0,18 нм ( рентгеновские снимки )
Термоядерное оружие (пиковая температура) ^[И]^[ф]	350 МК	350 миллионов °С	8.3 × 10 ⁻³ нм ( гамма излучение )
Национальная лаборатория Сандиа Z-машина ^[И]^[г]	2 ГК	2 миллиарда °С	1.4 × 10 ⁻³ нм (гамма излучение) ^[Ф]
Ядро большой массы звезда в свой последний день ^[И]^[час]	3 ГК	3 миллиарда °С	1 × 10 ⁻³ нм (гамма излучение)
Слияние двойного нейтрона звездная система ^[И]^[я]	350 ГК	350 миллиардов °С	8 × 10 ⁻⁶ нм (гамма излучение)
Релятивистский тяжелый Ионный коллайдер ^[И]^[105]	1 ТЗ	1 триллион °С	3 × 10 ⁻⁶ нм (гамма излучение)
Протон ЦЕРН против столкновения ядер ^[И]^[106]	10 ТК	10 триллионов °С	3 × 10 ⁻⁷ нм (гамма излучение)

^А Для венского стандарта средняя океанская вода при давлении в одну стандартную атмосферу ( 101,325 кПа ) при строгой калибровке по двухточечному определению термодинамической температуры.
^БЗначение 2500 К является приблизительным. Разница в 273,15 К между K и °C округляется до 300 К, чтобы избежать ложной точности значения Цельсия.
^СДля настоящего черного тела (которым не являются вольфрамовые нити). Излучательная способность вольфрамовой нити выше на более коротких длинах волн, из-за чего они кажутся белее.
^ДЭффективная температура фотосферы. Разница в 273,15 К между K и °C округляется до 273 К, чтобы избежать ложной точности значения Цельсия.
^И Разница в 273,15 К между K и °C находится в пределах точности этих значений.
^ФДля настоящего черного тела (которым не была плазма). Основное излучение машины Z исходило от 40 электронов МК (мягкое рентгеновское излучение) внутри плазмы.

См. также [ править ]

Температура атмосферы - физическая величина, выражающая тепло и холод в атмосфере.
Температура тела – способность организма поддерживать температуру тела в определенных пределах (терморегуляция).
Цветовая температура - свойство источников света, связанное с излучением черного тела.
Температура по сухому термометру - температура воздуха, измеренная термометром, защищенным от радиации и влаги.
Теплопроводность - процесс передачи тепла внутри объекта.
Конвективная теплопередача – передача тепла за счет комбинированного эффекта адвекции и диффузии.
Инструментальная запись температуры - измерения на месте, которые определяют температуру климатической системы Земли.
ISO 1 – стандартная температура ISO, 20°C.
Международная температурная шкала 1990 года ( ITS-90 ) – Практическая температурная шкала.
Лазерная шлирен-дефлектометрия
Список городов по средней температуре
Демон Максвелла - мысленный эксперимент 1867 года.
Порядки величины (температура) - сравнение широкого диапазона температур.
Температура наружного воздуха – авиационный термин
Планковская температура – единицы измерения определяются только физическими константами.
Шкала Ренкина - шкала абсолютной температуры в градусах Фаренгейта.
Релятивистская теплопроводность - модель, совместимая со специальной теорией относительности.
Спутниковые измерения температуры . Измерения температуры атмосферы, поверхности суши или моря с помощью спутников.
Шкала температуры - метод количественного измерения температуры.
Температура поверхности моря – температура воды вблизи поверхности океана.
Температура застоя
Тепловое излучение - Электромагнитное излучение, создаваемое тепловым движением частиц.
Термоцепция – ощущение и восприятие температуры.
Термодинамическая (абсолютная) температура - мера абсолютной температуры.
Термография - инфракрасное изображение, используемое для определения температуры.
Термометр – прибор для измерения температуры.
Виртуальная температура - Виртуальная температура участка влажного воздуха.
Температура по влажному термометру - кажущаяся температура, позволяющая оценить влияние на людей.
Температура по влажному термометру – температура, измеряемая термометром, покрытым смоченной водой тканью.

Примечания и ссылки [ править ]

Примечания

^ Указанные длины волн излучения относятся к черным телам, находящимся в равновесии. Рекомендуемое значение CODATA 2006: 2,897 7685 (51) × 10. ⁻³ m K используется для константы закона смещения Вина b .
^ Температура 450 ± 80 пК в бозе-эйнштейновском конденсате (БЭК) атомов натрия была достигнута в 2003 году исследователями Массачусетского технологического института . Цитирование: Охлаждение конденсатов Бозе-Эйнштейна ниже 500 пикокельвинов , AE Leanhardt et al ., Science 301 , 12 сентября 2003 г., стр. 1515. Максимальная длина волны излучения черного тела, зафиксированная в этом рекорде, составляет 6400 километров, что примерно соответствует радиусу Земли.
^ Пиковая длина волны эмиттанса 2,897,77 м . соответствует частоте 103,456 МГц
^ С 2019 года Кельвин теперь определяется постоянной Больцмана , так что тройная точка равна 273,16 ± 0,0001 К.
^ Измерение было произведено в 2002 году и имеет погрешность ±3 кельвина. Измерение 1989 года , заархивированное 11 февраля 2010 г. на Wayback Machine, дало значение 5777,0 ± 2,5 К. Цитирование: Обзор Солнца (конспекты лекций по физике Солнца в главе 1, подготовленные Отделом теоретической физики, Факультет физических наук, Университет Хельсинки).
^ Значение 350 МК — это максимальная пиковая температура термоядерного топлива в термоядерном оружии конфигурации Теллера-Улама (широко известном как водородная бомба ). Пиковые температуры в ядрах бомб деления типа «Гаджет» (широко известных как атомная бомба ) находятся в диапазоне от 50 до 100 МК. Образец цитирования: Часто задаваемые вопросы о ядерном оружии, 3.2.5. Вещество при высоких температурах. Ссылка на соответствующую веб-страницу. Архивировано 3 мая 2007 г. в Wayback Machine. Все ссылочные данные были собраны из общедоступных источников.
^ Пиковая температура для большого количества вещества была достигнута с помощью импульсной машины, используемой в экспериментах по физике термоядерного синтеза. Термин «объемное количество» отличает столкновения в ускорителях частиц, где высокая температура применяется только к остаткам двух субатомных частиц или ядер в любой данный момент. Температура >2 ГК была достигнута за период около десяти наносекунд во время выстрела Z1137 . Действительно, ионы железа и марганца в плазме в среднем составляли 3,58±0,41 ГК (309±35 кэВ) за 3 нс (от 112 до 115 нс). Ионно-вязкий нагрев в магнитогидродинамически неустойчивом Z-пинче при увеличении более 2 × 10 ⁹Кельвин , М.Г. Хейнс и др. , Physical Review Letters 96 (2006) 075003. Ссылка на пресс-релиз Сандии. Архивировано 30 мая 2010 г. в Wayback Machine.
^ Температура ядра звезды большой массы (> 8–11 масс Солнца) после того, как она покидает главную последовательность на диаграмме Герцшпрунга – Рассела и начинает альфа-процесс (который длится один день) синтеза кремния-28 в более тяжелые элементы в следующие ступени: сера–32 → аргон–36 → кальций–40 → титан–44 → хром–48 → железо–52 → никель–56. Через несколько минут после завершения эпизода звезда взрывается как сверхновая типа II . Цитата: Холланд, Артур; Уильямс, Марк. «Звездная эволюция: жизнь и смерть наших светящихся соседей» . ГС265 . Университет Мичигана. Архивировано из оригинала 16 января 2009 г. Более информативные ссылки можно найти здесь «Глава 21 Звездные взрывы» . Архивировано из оригинала 11 апреля 2013 г. Проверено 8 февраля 2016 г. , и здесь «Транс» . Архивировано из оригинала 14 августа 2011 г. Проверено 8 февраля 2016 г. , а краткий трактат НАСА о звездах находится здесь. «НАСА-Звезда» . Архивировано из оригинала 24 октября 2010 г. Проверено 12 октября 2010 г. .
^ На основе компьютерной модели, которая предсказала пиковую внутреннюю температуру 30 МэВ (350 ГК) во время слияния двойной системы нейтронных звезд (которое производит гамма-всплеск). Нейтронные звезды в модели имели массу 1,2 и 1,6 солнечных масс соответственно, примерно 20 км в диаметре и вращались вокруг своего барицентра (общего центра масс) с частотой около 390 Гц в течение последних нескольких миллисекунд, прежде чем они полностью слились. Часть 350 ГК представляла собой небольшой объем, расположенный в развивающемся общем ядре пары, диаметр которого изменялся примерно от 1 до 7 км в течение времени около 5 мс. Представьте себе два объекта размером с город с невообразимой плотностью, вращающихся вокруг друг друга на той же частоте, что и музыкальная нота G4 (28-я белая клавиша фортепиано). Также примечательно, что при 350 ГК средний нейтрон имеет колебательную скорость, составляющую 30% скорости света, а релятивистскую массу ( m 5% больше, чем его масса покоя ( m0 _{) на} ). Формирование тора при слиянии нейтронных звезд и хорошо локализованных коротких гамма-всплесках. Архивировано. 22 ноября 2017 г. в Wayback Machine , Р. Охслин и др . из Института астрофизики Макса Планка. Архивировано 3 апреля 2005 г. в Wayback Machine , arXiv:astro-ph/0507099 v2, 22 февраля 2006 г. Сводка в формате HTML. Архивировано 9 ноября 2010 г. в Wayback Machine .

Цитаты

^ Агентство Международной атомной энергии (1974 год). Тепловые выбросы на атомных электростанциях: управление ими и воздействие на окружающую среду: отчет, подготовленный группой экспертов по результатам заседания экспертной группы, состоявшегося в Вене 23–27 октября 1972 г. Международное агентство по атомной энергии.
^ Уоткинсон, Джон (2001). Искусство цифрового звука . Тейлор и Фрэнсис. ISBN 978-0-240-51587-8 .
^ Миддлтон, WEK (1966), стр. 89–105.
^ Джоанна Томпсон (14 октября 2021 г.). «Ученые только что побили рекорд самой низкой температуры, когда-либо зарегистрированной в лаборатории» . Живая наука . Проверено 28 апреля 2023 г.
^ Перейти обратно: ^а ^б Джейнс, ET (1965), стр. 391–398.
^ Перейти обратно: ^а ^б Криогенное общество. Архивировано 7 ноября 2020 г. в Wayback Machine (2019).
^ Перейти обратно: ^а ^б Проект резолюции A «О пересмотре Международной системы единиц (СИ)» для представления ГКМВ на ее 26-м заседании (2018 г.) (PDF) , заархивировано из оригинала (PDF) 29 апреля 2018 г. , получено в 2019 г. -10-20
^ Перейти обратно: ^а ^б ^с Трусделл, Калифорния (1980), разделы 11 B, 11H, стр. 306–310, 320–332.
^ Куинн, TJ (1983).
^ Гермер, Л.Х. (1925). «Распределение начальных скоростей среди термоэмиссионных электронов», Физ. Откр. , 25 : 795–807. здесь
^ Терви, К. (1990). «Проверка достоверности статистики Максвелла для электронов, термоионно эмитированных из оксидного катода», Европейский журнал физики , 11 (1): 51–59. здесь
^ Цеппенфельд, М., Энглерт, БГУ, Глекнер, Р., Прен, А., Миленц, М., Зоммер, К., ван Бюрен, Л.Д., Моч, М., Ремпе, Г. (2012).
^ Миллер, Дж. (2013).
^ Перейти обратно: ^а ^б де Подеста, М., Андервуд, Р., Саттон, Г., Моранц, П., Харрис, П., Марк, Д.Ф., Стюарт, Ф.М., Варга, Г., Мачин, М. (2013). Измерение постоянной Больцмана с низкой погрешностью, Metrologia , 50 (4): S213–S216, BIPM & IOP Publishing Ltd.
^ Куинн, TJ (1983), стр. 98–107.
^ Скули, Дж. Ф. (1986), стр. 138–143.
^ Куинн, TJ (1983), стр. 61–83.
^ Скули, Дж. Ф. (1986), стр. 115–138.
^ Адкинс, CJ (1968/1983), стр. 119–120.
^ Бухдал, HA (1966), стр. 137–138.
^ Tschoegl, NW (2000), стр. 88.
^ Перейти обратно: ^а ^б Ферми, Э. (1956). Термодинамика . Dover Publications (все еще издается). п. 48. уравнение (64) .
^ Томсон, В. (лорд Кельвин) (1848).
^ Томсон, В. (лорд Кельвин) (1851).
^ Партингтон, младший (1949), стр. 175–177.
^ Робертс, Дж. К., Миллер, А. Р. (1928/1960), стр. 321–322.
^ Куинн, ТиДжей (1983). Температура , Academic Press, Лондон, ISBN 0-12-569680-9 , стр. 160–162.
^ Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, стр. 47, 57.
^ Перейти обратно: ^а ^б ^с Мюнстер, А. (1970), Классическая термодинамика , перевод Э.С. Хальберштадта, Wiley – Interscience, Лондон, ISBN 0-471-62430-6 , стр. 49, 69.
^ Перейти обратно: ^а ^б Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , стр. 14–15, 214.
^ Перейти обратно: ^а ^б Каллен, Х.Б. (1960/1985), Термодинамика и введение в термостатистику (первое издание 1960 г.), второе издание 1985 г., John Wiley & Sons, Нью-Йорк, ISBN 0-471-86256-8 , стр. 146–148.
^ Кондепуди Д., Пригожин И. (1998). Современная термодинамика. От тепловых двигателей к диссипативным структурам , Джон Уайли, Чичестер, ISBN 0-471-97394-7 , стр. 115–116.
^ Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, с. 58.
^ Милн, Э.А. (1929). Влияние столкновений на монохроматическое радиационное равновесие, Ежемесячные уведомления Королевского астрономического общества , 88 : 493–502.
^ Дьярмати, И. (1970). Неравновесная термодинамика. Теория поля и вариационные принципы , перевод Э. Дьярмати и В. Ф. Хайнца, Springer, Берлин, стр. 63–66.
^ Глансдорф П., Пригожин И. (1971). Термодинамическая теория структуры, устойчивости и флуктуаций , Уайли, Лондон, ISBN 0-471-30280-5 , стр. 14–16.
^ Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , стр. 133–135.
^ Каллен, Х.Б. (1960/1985), Термодинамика и введение в термостатистику (первое издание 1960 г.), второе издание 1985 г., John Wiley & Sons, Нью-Йорк, ISBN 0-471-86256-8 , стр. 309–310.
^ Брайан, GH (1907). Термодинамика. Вводный трактат, посвященный главным образом первым принципам и их прямому применению , Б. Г. Тойбнер, Лейпциг, с. 3. «Термодинамика Джорджа Хартли Брайана» . Архивировано из оригинала 18 ноября 2011 г. Проверено 2 октября 2011 г.
^ Пиппард, AB (1957/1966), с. 18.
^ Адкинс, CJ (1968/1983), стр. 20.
^ Брайан, GH (1907). Термодинамика. Вводный трактат, посвященный главным образом первым принципам и их прямому применению , Б. Г. Тойбнер, Лейпциг, с. 5: «... когда о теле говорят, что оно становится все горячее или холоднее, всегда подразумевается повышение температуры, поскольку теплота и холодность тела являются качественными терминами, которые могут относиться только к температуре». «Термодинамика Джорджа Хартли Брайана» . Архивировано из оригинала 18 ноября 2011 г. Проверено 2 октября 2011 г.
^ Перейти обратно: ^а ^б ^с ^д Мах, Э. (1900). Принципы термодинамики. Историко-критическое развитие , Иоганн Амброзиус Барт, Лейпциг, раздел 22, стр. 56–57.
^ Перейти обратно: ^а ^б Серрин, Дж. (1986). Глава 1, «Очерк термодинамической структуры», стр. 3–32, особенно стр. 6, в «Новых перспективах термодинамики» под редакцией Дж. Серрина, Springer, Берлин, ISBN 3-540-15931-2 .
^ Максвелл, Дж. К. (1872). Теория тепла , третье издание, Лонгманс, Грин, Лондон, с. 32.
^ Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, стр. 39–40.
^ Планк, М. (1897/1903). Трактат по термодинамике , перевод А. Огга, Лонгманс, Грин, Лондон, стр. 1–2.
^ Планк, М. (1914), Теория теплового излучения. Архивировано 18 ноября 2011 г. в Wayback Machine , второе издание, переведено на английский М. Масиусом, Blakiston's Son & Co., Филадельфия, перепечатано Кессинджером.
^ Дж. С. Дагдейл (1996). Энтропия и ее физическая интерпретация . Тейлор и Фрэнсис. п. 13. ISBN 978-0-7484-0569-5 .
^ Ф. Рейф (1965). Основы статистической и теплофизики . МакГроу-Хилл. п. 102 . ISBN 9780070518001 .
^ М. Дж. Моран; Х. Н. Шапиро (2006). «1.6.1». Основы технической термодинамики (5-е изд.). Джон Вили и сыновья, ООО с. 14. ISBN 978-0-470-03037-0 .
^ Т.В. Леланд-младший «Основные принципы классической и статистической термодинамики» (PDF) . п. 14. Архивировано (PDF) из оригинала 28 сентября 2011 г. Следовательно, мы определяем температуру как движущую силу, которая вызывает передачу так называемого тепла.
^ Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, стр. 42, 103–117.
^ Битти, Дж. А., Оппенгейм, И. (1979). Принципы термодинамики , Научное издательство Elsevier, Амстердам, ISBN 978-0-444-41806-7 , с. 29.
^ Ландсберг, PT (1961). Термодинамика с квантовыми статистическими иллюстрациями , Interscience Publishers, Нью-Йорк, с. 17.
^ Томсен, Дж. С. (1962). «Переформулировка нулевого закона термодинамики» . Являюсь. Дж. Физ . 30 (4): 294–296. Бибкод : 1962AmJPh..30..294T . дои : 10.1119/1.1941991 .
^ Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longman's, Green & Co, Лондон, с. 45.
^ Перейти обратно: ^а ^б Питтери, М. (1984). Об аксиоматических основах температуры, Приложение G6, стр. 522–544, журнал Rational Thermodynamics , C. Truesdell, второе издание, Springer, Нью-Йорк, ISBN 0-387-90874-9 .
^ Трусделл, К., Бхарата, С. (1977). Концепции и логика классической термодинамики как теории тепловых двигателей, строго построенные на фундаменте, заложенном С. Карно и Ф. Ричем , Спрингер, Нью-Йорк, ISBN 0-387-07971-8 , с. 20.
^ Перейти обратно: ^а ^б Серрин, Дж. (1978). Концепции термодинамики в книге « Современные разработки в механике сплошной среды и уравнениях с частными производными». Труды Международного симпозиума по механике сплошной среды и уравнениям в частных производных, Рио-де-Жанейро, август 1977 г. , под редакцией Г.М. де Ла Пенья, Л.А.Дж. Медейроса, Северная Голландия, Амстердам, ISBN 0-444-85166-6 , стр. 411–451.
^ Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longmans, Green, Лондон, стр. 155–158.
^ Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, Раздел 95, стр. 68–69.
^ Бухдал, HA (1966), стр. 73.
^ Кондепуди, Д. (2008). Введение в современную термодинамику , Уайли, Чичестер, ISBN 978-0-470-01598-8 , раздел 32., стр. 106–108.
^ Грин, Дон; Перри, Роберт Х. (2008). Справочник инженеров-химиков Перри, восьмое издание (8-е изд.). Макгроу-Хилл Образование. п. 660. ИСБН 978-0071422949 .
^ Кельвин в брошюре SI , заархивированной 26 сентября 2007 г. в Wayback Machine.
^ "Абсолютный ноль" . Calphad.com. Архивировано из оригинала 8 июля 2011 г. Проверено 16 сентября 2010 г.
^ Определение, согласованное 26-й Генеральной конференцией мер и весов (CGPM). Архивировано 9 октября 2020 г. в Wayback Machine в ноябре 2018 г., реализовано 20 мая 2019 г.
^ Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Джа, Адитья; Кэмпбелл, Дуглас; Монтель, Клеменси; Уилсон, Филип Л. (30 июля 2023 г.). «Об ошибке континуума: является ли температура непрерывной функцией?» . Основы физики . 53 (4): 69. Бибкод : 2023FoPh...53...69J . дои : 10.1007/s10701-023-00713-x . ISSN 1572-9516 .
^ ван Стрин, Мария (01 октября 2015 г.). «Непрерывность в природе и математике: Больцман и Пуанкаре» . Синтезируйте . 192 (10): 3275–3295. дои : 10.1007/s11229-015-0701-9 . ISSN 1573-0964 . S2CID 255075377 .
^ Фанг, Г.; Уорд, Калифорния (1 января 1999 г.). «Температура, измеренная вблизи границы раздела испаряющейся жидкости» . Физический обзор E . 59 (1): 417–428. Бибкод : 1999PhRvE..59..417F . дои : 10.1103/PhysRevE.59.417 .
^ Ньюэлл, Гомер Э. (12 февраля 1960 г.). «Космическая среда: Поскольку человек с нетерпением ждет полета в космос, он находит внешние регионы не совсем неизвестными» . Наука . 131 (3398): 385–390. дои : 10.1126/science.131.3398.385 . ISSN 0036-8075 . ПМИД 14426791 .
^ Перейти обратно: ^а ^б Чен, Банда (01 августа 2022 г.). «О молекулярной картине и скачке межфазной температуры при испарении и конденсации» . Международный журнал тепломассообмена . 191 : 122845. arXiv : 2201.07318 . doi : 10.1016/j.ijheatmasstransfer.2022.122845 . ISSN 0017-9310 . S2CID 246036409 .
^ Перейти обратно: ^а ^б Кэхилл, Д; и другие. (27 декабря 2022 г.). «Наномасштабный тепловой транспорт» . Журнал прикладной физики . 93 (2): 793–818. дои : 10.1063/1.1524305 . hdl : 2027.42/70161 . S2CID 15327316 . Проверено 2 августа 2023 г.
^ Перейти обратно: ^а ^б Чен, Цзе; Сюй, Сянфань; Чжоу, Цзюнь; Ли, Баовэнь (22 апреля 2022 г.). «Межфазное термическое сопротивление: прошлое, настоящее и будущее» . Обзоры современной физики . 94 (2): 025002. Бибкод : 2022RvMP...94b5002C . doi : 10.1103/RevModPhys.94.025002 . S2CID 248350864 .
^ Перейти обратно: ^а ^б Аурсанд, Эскил; Итрехус, Тор (01 июля 2019 г.). «Сравнение моделей испарения кинетической теории для тонких пленок жидкости» . Международный журнал многофазного потока . 116 : 67–79. doi : 10.1016/j.ijmultiphaseflow.2019.04.007 . HDL : 11250/2594950 . ISSN 0301-9322 . S2CID 146056093 .
^ К. Каратеодори (1909). «Исследования по основам термодинамики» . Математические летописи . 67 (3): 355–386. дои : 10.1007/BF01450409 . S2CID 118230148 .
^ Свендсен, Роберт (март 2006 г.). «Статистическая механика коллоидов и определение энтропии Больцмана» (PDF) . Американский журнал физики . 74 (3): 187–190. Бибкод : 2006AmJPh..74..187S . дои : 10.1119/1.2174962 . S2CID 59471273 . Архивировано из оригинала (PDF) 28 февраля 2020 г.
^ Балеску, Р. (1975). Равновесная и неравновесная статистическая механика , Уайли, Нью-Йорк, ISBN 0-471-04600-0 , стр. 148–154.
^ Перейти обратно: ^а ^б Киттель, Чарльз ; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания WH Freeman. стр. 391–397. ISBN 978-0-7167-1088-2 .
^ Кондепуди, ДК (1987). «Микроскопические аспекты, вытекающие из второго закона». Основы физики . 17 (7): 713–722. Бибкод : 1987FoPh...17..713K . дои : 10.1007/BF01889544 . S2CID 120576357 .
^ Фейнмановские лекции по физике. 39–5 Закон идеального газа
^ «Значение CODATA 2022: молярная газовая постоянная» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ «Кинетическая теория» . galileo.phys.virginia.edu . Архивировано из оригинала 16 июля 2017 года . Проверено 27 января 2018 г.
^ Толман, RC (1938). Принципы статистической механики , Oxford University Press, Лондон, стр. 93, 655.
^ Питер Аткинс, Хулио де Паула (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. п. 9.
^ Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longman's, Green & Co, Лондон, с. 32.
^ Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , с. 23, «..., если существует температурный градиент, ... то для достижения однородной температуры должен возникнуть поток тепла ...».
^ Гуггенхайм, EA (1967). Термодинамика. Расширенное лечение для химиков и физиков , Издательство Северной Голландии. , Амстердам, (1-е издание 1949 г.) пятое издание 1965 г., с. 8: «...будут постепенно приспосабливаться, пока в конце концов не достигнут взаимного равновесия, после чего, конечно, дальнейших изменений не будет».
^ Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , с. 22.
^ Гуггенхайм, EA (1967). Термодинамика. Расширенное лечение для химиков и физиков , Издательство Северной Голландии. , Амстердам, (1-е издание 1949 г.) пятое издание 1965 г., с. 8: «Если две системы находятся в тепловом равновесии с третьей системой, то они находятся в тепловом равновесии друг с другом».
^ Бухдал, HA (1966). Концепции классической термодинамики , Издательство Кембриджского университета, Кембридж, с. 29: «...если каждая из двух систем находится в равновесии с третьей системой, то они находятся в равновесии друг с другом».
^ Перейти обратно: ^а ^б Планк, М. (1945). Трактат по термодинамике . Дуврские публикации. п. §90 и §137. уравнения (39), (40) и (65) .
^ Прати, Э. (2010). «Конечный квантовый большой канонический ансамбль и температура из одноэлектронной статистики для мезоскопического устройства». Дж. Стат. Мех . 1 (1): P01003. arXiv : 1001.2342 . Бибкод : 2010JSMTE..01..003P . дои : 10.1088/1742-5468/2010/01/P01003 . S2CID 118339343 . arxiv.org. Архивировано 22 ноября 2017 г. на Wayback Machine.
^ «Осуществление мечты Больцмана: компьютерное моделирование в современной статистической механике» (PDF) . Архивировано (PDF) из оригинала 13 апреля 2014 г. Проверено 11 апреля 2014 г.
^ Прати, Э.; и другие. (2010). «Измерение температуры мезоскопической электронной системы с помощью статистики одиночных электронов» . Письма по прикладной физике . 96 (11): 113109. arXiv : 1002.0037 . Бибкод : 2010АпФЛ..96к3109П . дои : 10.1063/1.3365204 . S2CID 119209143 . Архивировано из оригинала 14 мая 2016 г. Проверено 02 марта 2022 г. arxiv.org. Архивировано 22 ноября 2017 г. на Wayback Machine.
^ Школа водных наук. «Замороженный углекислый газ (сухой лед) сублимируется непосредственно в пар» . Геологическая служба США .
^ Гуггенхайм, Э.А. (1967) [1949], Термодинамика. Расширенное лечение химиков и физиков (пятое изд.), Амстердам: Издательство Северной Голландии. , п. 157 : «Невозможно никакой процедурой, какой бы идеализированной она ни была, снизить температуру любой системы до нулевой температуры за конечное число конечных операций».
^ Пиппард, AB (1957/1966). «Элементы классической термодинамики для продвинутых студентов-физиков» , оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Кембридж, стр. 51: « Никакая конечная серия процессов не достижима абсолютного нуля » .
^ Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, стр. 96: «Невозможно достичь абсолютного нуля в результате конечной последовательности операций».
^ Киттель, Чарльз ; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания WH Freeman. п. Приложение E. ISBN 978-0-7167-1088-2 .
^ СВС (03.08.2023). «Студия научной визуализации НАСА | Путеводитель по космическим температурам» . СВС . Проверено 6 августа 2023 г.
^ Это излучение Хокинга для черной дыры Шварцшильда массы M = 4,145 × 10. ⁶ М _☉ . Оно слишком слабое, чтобы его можно было наблюдать.
^ «Мировой рекорд по низким температурам» . Архивировано из оригинала 18 июня 2009 г. Проверено 5 мая 2009 г.
^ Результаты исследования Стефана Бата с использованием PHENIX. Архивировано 20 ноября 2008 г. в детекторе Wayback Machine на релятивистском коллайдере тяжелых ионов. Архивировано 3 марта 2016 г. в Wayback Machine в Брукхейвенской национальной лаборатории. Архивировано 24 июня 2012 г. в Wayback . Машина в Аптоне, Нью-Йорк. Бат исследовал столкновения золота и золота, дейтрона и золота и протон-протонные столкновения, чтобы проверить теорию квантовой хромодинамики, теорию сильной силы, удерживающей атомные ядра вместе. Ссылка на выпуск новостей. Архивировано 11 февраля 2009 г. в Wayback Machine.
^ Как физики изучают частицы? Архивировано 11 октября 2007 г. в Wayback Machine ЦЕРН . Архивировано 7 июля 2012 г. в Wayback Machine .

Библиография цитируемых ссылок [ править ]

Адкинс, CJ (1968/1983). Равновесная термодинамика (1-е издание, 1968 г.), третье издание, 1983 г., издательство Кембриджского университета, Кембридж, Великобритания, ISBN 0-521-25445-0 .
Бухдал, ХА (1966). Концепции классической термодинамики , Издательство Кембриджского университета, Кембридж.
Джейнс, ET (1965). Гиббс против энтропии Больцмана, Американский журнал физики , 33 (5), 391–398.
Миддлтон, ВЕК (1966). История термометра и его использования в метрологии , Johns Hopkins Press, Балтимор.
Миллер, Дж (2013). «Охлаждение молекул оптоэлектрическим способом» . Физика сегодня . 66 (1): 12–14. Бибкод : 2013ФТ....66а..12М . дои : 10.1063/pt.3.1840 .
Партингтон-младший (1949). Расширенный трактат по физической химии , том 1, Фундаментальные принципы. Свойства газов , Longmans, Green & Co., Лондон, стр. 175–177.
Пиппард, AB (1957/1966). Элементы классической термодинамики для студентов-физиков , оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Кембридж, Великобритания.
Куинн, Ти Джей (1983). Температура , Academic Press, Лондон, ISBN 0-12-569680-9 .
Скули, Дж. Ф. (1986). Термометрия , CRC Press, Бока-Ратон, ISBN 0-8493-5833-7 .
Робертс, Дж. К., Миллер, А. Р. (1928/1960). Тепло и термодинамика (первое издание, 1928 г.), пятое издание, Blackie & Son Limited, Глазго.
Томсон, В. (лорд Кельвин) (1848). По абсолютной термометрической шкале, основанной на теории движущей силы тепла Карно и рассчитанной на основе наблюдений Рено, Proc. Кэмб. Фил. Соц. (1843/1863) 1 , № 5: 66–71.
Томсон, В. (лорд Кельвин) (март 1851 г.). «О динамической теории тепла с численными результатами, полученными на основе эквивалента тепловой единицы г-на Джоуля, и наблюдений М. Рено над паром». Труды Королевского общества Эдинбурга . XX (часть II): 261–268, 289–298.
Трусделл, Калифорния (1980). Трагикомическая история термодинамики, 1822–1854 гг. , Спрингер, Нью-Йорк, ISBN 0-387-90403-4 .
Чогль, Северо-Запад (2000). Основы равновесной и стационарной термодинамики , Elsevier, Амстердам, ISBN 0-444-50426-5 .
Цеппенфельд, М.; Энглерт, БГУ; Глекнер, Р.; Прен, А.; Миленц, М.; Соммер, К.; ван Бюрен, доктор медицинских наук; Мотч, М.; Ремпе, Г. (2012). «Сизифовое охлаждение электрически захваченных многоатомных молекул». Природа . 491 (7425): 570–573. arXiv : 1208.0046 . Бибкод : 2012Natur.491..570Z . дои : 10.1038/nature11595 . ПМИД 23151480 . S2CID 4367940 .

Дальнейшее чтение [ править ]

Чанг, Хасок (2004). Изобретение температуры: измерение и научный прогресс . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-517127-3 .
Земанский, Марк Уолдо (1964). Температуры очень низкие и очень высокие . Принстон, Нью-Джерси: Ван Ностранд.

Внешние ссылки [ править ]

Текущая карта глобальной приземной температуры

[103] Указанные длины волн излучения относятся к черным телам, находящимся в равновесии. Рекомендуемое значение CODATA 2006: 2,897 7685 (51) × 10. ⁻³ m K используется для константы закона смещения Вина b .

[recordcold-106] Температура 450 ± 80 пК в бозе-эйнштейновском конденсате (БЭК) атомов натрия была достигнута в 2003 году исследователями Массачусетского технологического института . Цитирование: Охлаждение конденсатов Бозе-Эйнштейна ниже 500 пикокельвинов , AE Leanhardt et al ., Science 301 , 12 сентября 2003 г., стр. 1515. Максимальная длина волны излучения черного тела, зафиксированная в этом рекорде, составляет 6400 километров, что примерно соответствует радиусу Земли.

[107] Пиковая длина волны эмиттанса 2,897,77 м . соответствует частоте 103,456 МГц

[108] С 2019 года Кельвин теперь определяется постоянной Больцмана , так что тройная точка равна 273,16 ± 0,0001 К.

[109] Измерение было произведено в 2002 году и имеет погрешность ±3 кельвина. Измерение 1989 года , заархивированное 11 февраля 2010 г. на Wayback Machine, дало значение 5777,0 ± 2,5 К. Цитирование: Обзор Солнца (конспекты лекций по физике Солнца в главе 1, подготовленные Отделом теоретической физики, Факультет физических наук, Университет Хельсинки).

[110] Значение 350 МК — это максимальная пиковая температура термоядерного топлива в термоядерном оружии конфигурации Теллера-Улама (широко известном как водородная бомба ). Пиковые температуры в ядрах бомб деления типа «Гаджет» (широко известных как атомная бомба ) находятся в диапазоне от 50 до 100 МК. Образец цитирования: Часто задаваемые вопросы о ядерном оружии, 3.2.5. Вещество при высоких температурах. Ссылка на соответствующую веб-страницу. Архивировано 3 мая 2007 г. в Wayback Machine. Все ссылочные данные были собраны из общедоступных источников.

[111] Пиковая температура для большого количества вещества была достигнута с помощью импульсной машины, используемой в экспериментах по физике термоядерного синтеза. Термин «объемное количество» отличает столкновения в ускорителях частиц, где высокая температура применяется только к остаткам двух субатомных частиц или ядер в любой данный момент. Температура >2 ГК была достигнута за период около десяти наносекунд во время выстрела Z1137 . Действительно, ионы железа и марганца в плазме в среднем составляли 3,58±0,41 ГК (309±35 кэВ) за 3 нс (от 112 до 115 нс). Ионно-вязкий нагрев в магнитогидродинамически неустойчивом Z-пинче при увеличении более 2 × 10 ⁹Кельвин , М.Г. Хейнс и др. , Physical Review Letters 96 (2006) 075003. Ссылка на пресс-релиз Сандии. Архивировано 30 мая 2010 г. в Wayback Machine.

[112] Температура ядра звезды большой массы (> 8–11 масс Солнца) после того, как она покидает главную последовательность на диаграмме Герцшпрунга – Рассела и начинает альфа-процесс (который длится один день) синтеза кремния-28 в более тяжелые элементы в следующие ступени: сера–32 → аргон–36 → кальций–40 → титан–44 → хром–48 → железо–52 → никель–56. Через несколько минут после завершения эпизода звезда взрывается как сверхновая типа II . Цитата: Холланд, Артур; Уильямс, Марк. «Звездная эволюция: жизнь и смерть наших светящихся соседей» . ГС265 . Университет Мичигана. Архивировано из оригинала 16 января 2009 г. Более информативные ссылки можно найти здесь «Глава 21 Звездные взрывы» . Архивировано из оригинала 11 апреля 2013 г. Проверено 8 февраля 2016 г. , и здесь «Транс» . Архивировано из оригинала 14 августа 2011 г. Проверено 8 февраля 2016 г. , а краткий трактат НАСА о звездах находится здесь. «НАСА-Звезда» . Архивировано из оригинала 24 октября 2010 г. Проверено 12 октября 2010 г. .

[113] На основе компьютерной модели, которая предсказала пиковую внутреннюю температуру 30 МэВ (350 ГК) во время слияния двойной системы нейтронных звезд (которое производит гамма-всплеск). Нейтронные звезды в модели имели массу 1,2 и 1,6 солнечных масс соответственно, примерно 20 км в диаметре и вращались вокруг своего барицентра (общего центра масс) с частотой около 390 Гц в течение последних нескольких миллисекунд, прежде чем они полностью слились. Часть 350 ГК представляла собой небольшой объем, расположенный в развивающемся общем ядре пары, диаметр которого изменялся примерно от 1 до 7 км в течение времени около 5 мс. Представьте себе два объекта размером с город с невообразимой плотностью, вращающихся вокруг друг друга на той же частоте, что и музыкальная нота G4 (28-я белая клавиша фортепиано). Также примечательно, что при 350 ГК средний нейтрон имеет колебательную скорость, составляющую 30% скорости света, а релятивистскую массу ( m 5% больше, чем его масса покоя ( m0 _{) на} ). Формирование тора при слиянии нейтронных звезд и хорошо локализованных коротких гамма-всплесках. Архивировано. 22 ноября 2017 г. в Wayback Machine , Р. Охслин и др . из Института астрофизики Макса Планка. Архивировано 3 апреля 2005 г. в Wayback Machine , arXiv:astro-ph/0507099 v2, 22 февраля 2006 г. Сводка в формате HTML. Архивировано 9 ноября 2010 г. в Wayback Machine .

[1] Агентство Международной атомной энергии (1974 год). Тепловые выбросы на атомных электростанциях: управление ими и воздействие на окружающую среду: отчет, подготовленный группой экспертов по результатам заседания экспертной группы, состоявшегося в Вене 23–27 октября 1972 г. Международное агентство по атомной энергии.

[2] Уоткинсон, Джон (2001). Искусство цифрового звука . Тейлор и Фрэнсис. ISBN 978-0-240-51587-8 .

[3] Миддлтон, WEK (1966), стр. 89–105.

[4] Джоанна Томпсон (14 октября 2021 г.). «Ученые только что побили рекорд самой низкой температуры, когда-либо зарегистрированной в лаборатории» . Живая наука . Проверено 28 апреля 2023 г.

[BoltzmannvsGibbs-5] Перейти обратно: ^а ^б Джейнс, ET (1965), стр. 391–398.

[Boltzmann_constant-6] Перейти обратно: ^а ^б Криогенное общество. Архивировано 7 ноября 2020 г. в Wayback Machine (2019).

[draft-resolution-A-7] Перейти обратно: ^а ^б Проект резолюции A «О пересмотре Международной системы единиц (СИ)» для представления ГКМВ на ее 26-м заседании (2018 г.) (PDF) , заархивировано из оригинала (PDF) 29 апреля 2018 г. , получено в 2019 г. -10-20

[Truesdell_1980-8] Перейти обратно: ^а ^б ^с Трусделл, Калифорния (1980), разделы 11 B, 11H, стр. 306–310, 320–332.

[9] Куинн, TJ (1983).

[10] Гермер, Л.Х. (1925). «Распределение начальных скоростей среди термоэмиссионных электронов», Физ. Откр. , 25 : 795–807. здесь

[11] Терви, К. (1990). «Проверка достоверности статистики Максвелла для электронов, термоионно эмитированных из оксидного катода», Европейский журнал физики , 11 (1): 51–59. здесь

[12] Цеппенфельд, М., Энглерт, БГУ, Глекнер, Р., Прен, А., Миленц, М., Зоммер, К., ван Бюрен, Л.Д., Моч, М., Ремпе, Г. (2012).

[13] Миллер, Дж. (2013).

[de_Podesta-14] Перейти обратно: ^а ^б де Подеста, М., Андервуд, Р., Саттон, Г., Моранц, П., Харрис, П., Марк, Д.Ф., Стюарт, Ф.М., Варга, Г., Мачин, М. (2013). Измерение постоянной Больцмана с низкой погрешностью, Metrologia , 50 (4): S213–S216, BIPM & IOP Publishing Ltd.

[15] Куинн, TJ (1983), стр. 98–107.

[16] Скули, Дж. Ф. (1986), стр. 138–143.

[17] Куинн, TJ (1983), стр. 61–83.

[18] Скули, Дж. Ф. (1986), стр. 115–138.

[19] Адкинс, CJ (1968/1983), стр. 119–120.

[20] Бухдал, HA (1966), стр. 137–138.

[21] Tschoegl, NW (2000), стр. 88.

[FermiBook-22] Перейти обратно: ^а ^б Ферми, Э. (1956). Термодинамика . Dover Publications (все еще издается). п. 48. уравнение (64) .

[23] Томсон, В. (лорд Кельвин) (1848).

[24] Томсон, В. (лорд Кельвин) (1851).

[25] Партингтон, младший (1949), стр. 175–177.

[26] Робертс, Дж. К., Миллер, А. Р. (1928/1960), стр. 321–322.

[27] Куинн, ТиДжей (1983). Температура , Academic Press, Лондон, ISBN 0-12-569680-9 , стр. 160–162.

[28] Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, стр. 47, 57.

[Munster_49_69-29] Перейти обратно: ^а ^б ^с Мюнстер, А. (1970), Классическая термодинамика , перевод Э.С. Хальберштадта, Wiley – Interscience, Лондон, ISBN 0-471-62430-6 , стр. 49, 69.

[Bailyn_14_214-30] Перейти обратно: ^а ^б Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , стр. 14–15, 214.

[Callen_146–148-31] Перейти обратно: ^а ^б Каллен, Х.Б. (1960/1985), Термодинамика и введение в термостатистику (первое издание 1960 г.), второе издание 1985 г., John Wiley & Sons, Нью-Йорк, ISBN 0-471-86256-8 , стр. 146–148.

[32] Кондепуди Д., Пригожин И. (1998). Современная термодинамика. От тепловых двигателей к диссипативным структурам , Джон Уайли, Чичестер, ISBN 0-471-97394-7 , стр. 115–116.

[33] Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, с. 58.

[34] Милн, Э.А. (1929). Влияние столкновений на монохроматическое радиационное равновесие, Ежемесячные уведомления Королевского астрономического общества , 88 : 493–502.

[35] Дьярмати, И. (1970). Неравновесная термодинамика. Теория поля и вариационные принципы , перевод Э. Дьярмати и В. Ф. Хайнца, Springer, Берлин, стр. 63–66.

[36] Глансдорф П., Пригожин И. (1971). Термодинамическая теория структуры, устойчивости и флуктуаций , Уайли, Лондон, ISBN 0-471-30280-5 , стр. 14–16.

[37] Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , стр. 133–135.

[38] Каллен, Х.Б. (1960/1985), Термодинамика и введение в термостатистику (первое издание 1960 г.), второе издание 1985 г., John Wiley & Sons, Нью-Йорк, ISBN 0-471-86256-8 , стр. 309–310.

[39] Брайан, GH (1907). Термодинамика. Вводный трактат, посвященный главным образом первым принципам и их прямому применению , Б. Г. Тойбнер, Лейпциг, с. 3. «Термодинамика Джорджа Хартли Брайана» . Архивировано из оригинала 18 ноября 2011 г. Проверено 2 октября 2011 г.

[40] Пиппард, AB (1957/1966), с. 18.

[41] Адкинс, CJ (1968/1983), стр. 20.

[42] Брайан, GH (1907). Термодинамика. Вводный трактат, посвященный главным образом первым принципам и их прямому применению , Б. Г. Тойбнер, Лейпциг, с. 5: «... когда о теле говорят, что оно становится все горячее или холоднее, всегда подразумевается повышение температуры, поскольку теплота и холодность тела являются качественными терминами, которые могут относиться только к температуре». «Термодинамика Джорджа Хартли Брайана» . Архивировано из оригинала 18 ноября 2011 г. Проверено 2 октября 2011 г.

[Mach_1900-43] Перейти обратно: ^а ^б ^с ^д Мах, Э. (1900). Принципы термодинамики. Историко-критическое развитие , Иоганн Амброзиус Барт, Лейпциг, раздел 22, стр. 56–57.

[Serrin_1986-44] Перейти обратно: ^а ^б Серрин, Дж. (1986). Глава 1, «Очерк термодинамической структуры», стр. 3–32, особенно стр. 6, в «Новых перспективах термодинамики» под редакцией Дж. Серрина, Springer, Берлин, ISBN 3-540-15931-2 .

[Maxwell_1872-45] Максвелл, Дж. К. (1872). Теория тепла , третье издание, Лонгманс, Грин, Лондон, с. 32.

[Tait_1884_39-40-46] Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, стр. 39–40.

[Planck_1897-47] Планк, М. (1897/1903). Трактат по термодинамике , перевод А. Огга, Лонгманс, Грин, Лондон, стр. 1–2.

[48] Планк, М. (1914), Теория теплового излучения. Архивировано 18 ноября 2011 г. в Wayback Machine , второе издание, переведено на английский М. Масиусом, Blakiston's Son & Co., Филадельфия, перепечатано Кессинджером.

[dugdale-49] Дж. С. Дагдейл (1996). Энтропия и ее физическая интерпретация . Тейлор и Фрэнсис. п. 13. ISBN 978-0-7484-0569-5 .

[reif-50] Ф. Рейф (1965). Основы статистической и теплофизики . МакГроу-Хилл. п. 102 . ISBN 9780070518001 .

[Moran-51] М. Дж. Моран; Х. Н. Шапиро (2006). «1.6.1». Основы технической термодинамики (5-е изд.). Джон Вили и сыновья, ООО с. 14. ISBN 978-0-470-03037-0 .

[52] Т.В. Леланд-младший «Основные принципы классической и статистической термодинамики» (PDF) . п. 14. Архивировано (PDF) из оригинала 28 сентября 2011 г. Следовательно, мы определяем температуру как движущую силу, которая вызывает передачу так называемого тепла.

[53] Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, стр. 42, 103–117.

[54] Битти, Дж. А., Оппенгейм, И. (1979). Принципы термодинамики , Научное издательство Elsevier, Амстердам, ISBN 978-0-444-41806-7 , с. 29.

[55] Ландсберг, PT (1961). Термодинамика с квантовыми статистическими иллюстрациями , Interscience Publishers, Нью-Йорк, с. 17.

[56] Томсен, Дж. С. (1962). «Переформулировка нулевого закона термодинамики» . Являюсь. Дж. Физ . 30 (4): 294–296. Бибкод : 1962AmJPh..30..294T . дои : 10.1119/1.1941991 .

[57] Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longman's, Green & Co, Лондон, с. 45.

[Pitteri_1984-58] Перейти обратно: ^а ^б Питтери, М. (1984). Об аксиоматических основах температуры, Приложение G6, стр. 522–544, журнал Rational Thermodynamics , C. Truesdell, второе издание, Springer, Нью-Йорк, ISBN 0-387-90874-9 .

[59] Трусделл, К., Бхарата, С. (1977). Концепции и логика классической термодинамики как теории тепловых двигателей, строго построенные на фундаменте, заложенном С. Карно и Ф. Ричем , Спрингер, Нью-Йорк, ISBN 0-387-07971-8 , с. 20.

[Serrin_1978-60] Перейти обратно: ^а ^б Серрин, Дж. (1978). Концепции термодинамики в книге « Современные разработки в механике сплошной среды и уравнениях с частными производными». Труды Международного симпозиума по механике сплошной среды и уравнениям в частных производных, Рио-де-Жанейро, август 1977 г. , под редакцией Г.М. де Ла Пенья, Л.А.Дж. Медейроса, Северная Голландия, Амстердам, ISBN 0-444-85166-6 , стр. 411–451.

[Maxwell_1872_155-158-61] Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longmans, Green, Лондон, стр. 155–158.

[Tait_1884_68-69-62] Тейт, PG (1884). Heat , Macmillan, Лондон, Глава VII, Раздел 95, стр. 68–69.

[63] Бухдал, HA (1966), стр. 73.

[64] Кондепуди, Д. (2008). Введение в современную термодинамику , Уайли, Чичестер, ISBN 978-0-470-01598-8 , раздел 32., стр. 106–108.

[65] Грин, Дон; Перри, Роберт Х. (2008). Справочник инженеров-химиков Перри, восьмое издание (8-е изд.). Макгроу-Хилл Образование. п. 660. ИСБН 978-0071422949 .

[66] Кельвин в брошюре SI , заархивированной 26 сентября 2007 г. в Wayback Machine.

[67] "Абсолютный ноль" . Calphad.com. Архивировано из оригинала 8 июля 2011 г. Проверено 16 сентября 2010 г.

[68] Определение, согласованное 26-й Генеральной конференцией мер и весов (CGPM). Архивировано 9 октября 2020 г. в Wayback Machine в ноябре 2018 г., реализовано 20 мая 2019 г.

[:0-69] Перейти обратно: ^а ^б ^с ^д ^Это ^ж ^г Джа, Адитья; Кэмпбелл, Дуглас; Монтель, Клеменси; Уилсон, Филип Л. (30 июля 2023 г.). «Об ошибке континуума: является ли температура непрерывной функцией?» . Основы физики . 53 (4): 69. Бибкод : 2023FoPh...53...69J . дои : 10.1007/s10701-023-00713-x . ISSN 1572-9516 .

[70] ван Стрин, Мария (01 октября 2015 г.). «Непрерывность в природе и математике: Больцман и Пуанкаре» . Синтезируйте . 192 (10): 3275–3295. дои : 10.1007/s11229-015-0701-9 . ISSN 1573-0964 . S2CID 255075377 .

[71] Фанг, Г.; Уорд, Калифорния (1 января 1999 г.). «Температура, измеренная вблизи границы раздела испаряющейся жидкости» . Физический обзор E . 59 (1): 417–428. Бибкод : 1999PhRvE..59..417F . дои : 10.1103/PhysRevE.59.417 .

[72] Ньюэлл, Гомер Э. (12 февраля 1960 г.). «Космическая среда: Поскольку человек с нетерпением ждет полета в космос, он находит внешние регионы не совсем неизвестными» . Наука . 131 (3398): 385–390. дои : 10.1126/science.131.3398.385 . ISSN 0036-8075 . ПМИД 14426791 .

[:1-73] Перейти обратно: ^а ^б Чен, Банда (01 августа 2022 г.). «О молекулярной картине и скачке межфазной температуры при испарении и конденсации» . Международный журнал тепломассообмена . 191 : 122845. arXiv : 2201.07318 . doi : 10.1016/j.ijheatmasstransfer.2022.122845 . ISSN 0017-9310 . S2CID 246036409 .

[:2-74] Перейти обратно: ^а ^б Кэхилл, Д; и другие. (27 декабря 2022 г.). «Наномасштабный тепловой транспорт» . Журнал прикладной физики . 93 (2): 793–818. дои : 10.1063/1.1524305 . hdl : 2027.42/70161 . S2CID 15327316 . Проверено 2 августа 2023 г.

[:3-75] Перейти обратно: ^а ^б Чен, Цзе; Сюй, Сянфань; Чжоу, Цзюнь; Ли, Баовэнь (22 апреля 2022 г.). «Межфазное термическое сопротивление: прошлое, настоящее и будущее» . Обзоры современной физики . 94 (2): 025002. Бибкод : 2022RvMP...94b5002C . doi : 10.1103/RevModPhys.94.025002 . S2CID 248350864 .

[:4-76] Перейти обратно: ^а ^б Аурсанд, Эскил; Итрехус, Тор (01 июля 2019 г.). «Сравнение моделей испарения кинетической теории для тонких пленок жидкости» . Международный журнал многофазного потока . 116 : 67–79. doi : 10.1016/j.ijmultiphaseflow.2019.04.007 . HDL : 11250/2594950 . ISSN 0301-9322 . S2CID 146056093 .

[caratheodory-77] К. Каратеодори (1909). «Исследования по основам термодинамики» . Математические летописи . 67 (3): 355–386. дои : 10.1007/BF01450409 . S2CID 118230148 .

[78] Свендсен, Роберт (март 2006 г.). «Статистическая механика коллоидов и определение энтропии Больцмана» (PDF) . Американский журнал физики . 74 (3): 187–190. Бибкод : 2006AmJPh..74..187S . дои : 10.1119/1.2174962 . S2CID 59471273 . Архивировано из оригинала (PDF) 28 февраля 2020 г.

[79] Балеску, Р. (1975). Равновесная и неравновесная статистическая механика , Уайли, Нью-Йорк, ISBN 0-471-04600-0 , стр. 148–154.

[K&K_391_397-80] Перейти обратно: ^а ^б Киттель, Чарльз ; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания WH Freeman. стр. 391–397. ISBN 978-0-7167-1088-2 .

[81] Кондепуди, ДК (1987). «Микроскопические аспекты, вытекающие из второго закона». Основы физики . 17 (7): 713–722. Бибкод : 1987FoPh...17..713K . дои : 10.1007/BF01889544 . S2CID 120576357 .

[82] Фейнмановские лекции по физике. 39–5 Закон идеального газа

[physconst-R-83] «Значение CODATA 2022: молярная газовая постоянная» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[84] «Кинетическая теория» . galileo.phys.virginia.edu . Архивировано из оригинала 16 июля 2017 года . Проверено 27 января 2018 г.

[85] Толман, RC (1938). Принципы статистической механики , Oxford University Press, Лондон, стр. 93, 655.

[atkins-86] Питер Аткинс, Хулио де Паула (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. п. 9.

[87] Максвелл, Дж. К. (1872). Теория тепла , третье издание, Longman's, Green & Co, Лондон, с. 32.

[88] Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , с. 23, «..., если существует температурный градиент, ... то для достижения однородной температуры должен возникнуть поток тепла ...».

[89] Гуггенхайм, EA (1967). Термодинамика. Расширенное лечение для химиков и физиков , Издательство Северной Голландии. , Амстердам, (1-е издание 1949 г.) пятое издание 1965 г., с. 8: «...будут постепенно приспосабливаться, пока в конце концов не достигнут взаимного равновесия, после чего, конечно, дальнейших изменений не будет».

[90] Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3 , с. 22.

[91] Гуггенхайм, EA (1967). Термодинамика. Расширенное лечение для химиков и физиков , Издательство Северной Голландии. , Амстердам, (1-е издание 1949 г.) пятое издание 1965 г., с. 8: «Если две системы находятся в тепловом равновесии с третьей системой, то они находятся в тепловом равновесии друг с другом».

[92] Бухдал, HA (1966). Концепции классической термодинамики , Издательство Кембриджского университета, Кембридж, с. 29: «...если каждая из двух систем находится в равновесии с третьей системой, то они находятся в равновесии друг с другом».

[PlanckBook-93] Перейти обратно: ^а ^б Планк, М. (1945). Трактат по термодинамике . Дуврские публикации. п. §90 и §137. уравнения (39), (40) и (65) .

[finense-94] Прати, Э. (2010). «Конечный квантовый большой канонический ансамбль и температура из одноэлектронной статистики для мезоскопического устройства». Дж. Стат. Мех . 1 (1): P01003. arXiv : 1001.2342 . Бибкод : 2010JSMTE..01..003P . дои : 10.1088/1742-5468/2010/01/P01003 . S2CID 118339343 . arxiv.org. Архивировано 22 ноября 2017 г. на Wayback Machine.

[95] «Осуществление мечты Больцмана: компьютерное моделирование в современной статистической механике» (PDF) . Архивировано (PDF) из оригинала 13 апреля 2014 г. Проверено 11 апреля 2014 г.

[singlepart-96] Прати, Э.; и другие. (2010). «Измерение температуры мезоскопической электронной системы с помощью статистики одиночных электронов» . Письма по прикладной физике . 96 (11): 113109. arXiv : 1002.0037 . Бибкод : 2010АпФЛ..96к3109П . дои : 10.1063/1.3365204 . S2CID 119209143 . Архивировано из оригинала 14 мая 2016 г. Проверено 02 марта 2022 г. arxiv.org. Архивировано 22 ноября 2017 г. на Wayback Machine.

[97] Школа водных наук. «Замороженный углекислый газ (сухой лед) сублимируется непосредственно в пар» . Геологическая служба США .

[98] Гуггенхайм, Э.А. (1967) [1949], Термодинамика. Расширенное лечение химиков и физиков (пятое изд.), Амстердам: Издательство Северной Голландии. , п. 157 : «Невозможно никакой процедурой, какой бы идеализированной она ни была, снизить температуру любой системы до нулевой температуры за конечное число конечных операций».

[99] Пиппард, AB (1957/1966). «Элементы классической термодинамики для продвинутых студентов-физиков» , оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Кембридж, стр. 51: « Никакая конечная серия процессов не достижима абсолютного нуля » .

[100] Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс, стр. 96: «Невозможно достичь абсолютного нуля в результате конечной последовательности операций».

[101] Киттель, Чарльз ; Кремер, Герберт (1980). Теплофизика (2-е изд.). Компания WH Freeman. п. Приложение E. ISBN 978-0-7167-1088-2 .

[102] СВС (03.08.2023). «Студия научной визуализации НАСА | Путеводитель по космическим температурам» . СВС . Проверено 6 августа 2023 г.

[104] Это излучение Хокинга для черной дыры Шварцшильда массы M = 4,145 × 10. ⁶ М _☉ . Оно слишком слабое, чтобы его можно было наблюдать.

[ltl-105] «Мировой рекорд по низким температурам» . Архивировано из оригинала 18 июня 2009 г. Проверено 5 мая 2009 г.

[114] Результаты исследования Стефана Бата с использованием PHENIX. Архивировано 20 ноября 2008 г. в детекторе Wayback Machine на релятивистском коллайдере тяжелых ионов. Архивировано 3 марта 2016 г. в Wayback Machine в Брукхейвенской национальной лаборатории. Архивировано 24 июня 2012 г. в Wayback . Машина в Аптоне, Нью-Йорк. Бат исследовал столкновения золота и золота, дейтрона и золота и протон-протонные столкновения, чтобы проверить теорию квантовой хромодинамики, теорию сильной силы, удерживающей атомные ядра вместе. Ссылка на выпуск новостей. Архивировано 11 февраля 2009 г. в Wayback Machine.

[115] Как физики изучают частицы? Архивировано 11 октября 2007 г. в Wayback Machine ЦЕРН . Архивировано 7 июля 2012 г. в Wayback Machine .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[99]

[100]

v т Это Метеорологические данные и переменные
General	Adiabatic processes Advection Buoyancy Lapse rate Lightning Surface solar radiation Surface weather analysis Visibility Vorticity Wind Wind shear
Condensation	Cloud Cloud condensation nuclei (CCN) Fog Convective condensation level (CCL) Lifted condensation level (LCL) Precipitable water Precipitation Water vapor
Convection	Convective available potential energy (CAPE) Convective inhibition (CIN) Convective instability Convective momentum transport Conditional symmetric instability Convective temperature (T_c) Equilibrium level (EL) Free convective layer (FCL) Helicity K Index Level of free convection (LFC) Lifted index (LI) Maximum parcel level (MPL) Bulk Richardson number (BRN)
Temperature	Dew point (T_d) Dew point depression Dry-bulb temperature Equivalent temperature (T_e) Forest fire weather index Haines Index Heat index Humidex Humidity Relative humidity (RH) Mixing ratio Potential temperature (θ) Equivalent potential temperature (θ_e) Sea surface temperature (SST) Temperature anomaly Thermodynamic temperature Vapor pressure Virtual temperature Wet-bulb temperature Wet-bulb globe temperature Wet-bulb potential temperature Wind chill
Pressure	Atmospheric pressure Baroclinity Barotropicity Pressure gradient Pressure-gradient force (PGF)
Velocity	Maximum potential intensity