Отрицательная температура

Шкала преобразования температуры/холода SI : температуры по шкале Кельвина показаны синим цветом (шкала Цельсия - зеленым, шкала Фаренгейта - красным), значения холода в гигабайтах на наноджоуль показаны черным. Бесконечная температура (нулевая холодность) показана вверху диаграммы; положительные значения холода/температуры находятся справа, отрицательные значения – слева.

Некоторые системы могут достигать отрицательной термодинамической температуры ; то есть их температура может быть выражена как отрицательная величина по шкале Кельвина или Ренкина . Это следует отличать от температур, выраженных отрицательными числами по нетермодинамическим шкалам Цельсия или Фаренгейта , которые, тем не менее, выше абсолютного нуля . Система с действительно отрицательной температурой по шкале Кельвина горячее , чем любая система с положительной температурой. Если системы с отрицательной температурой и системой с положительной температурой вступают в контакт, тепло перетечет от системы с отрицательной температурой к системе с положительной температурой. Стандартный пример такой системы — инверсная населенность в лазерной физике .

Термодинамические системы с неограниченным фазовым пространством не могут достичь отрицательных температур: добавление тепла всегда увеличивает их энтропию . Возможность уменьшения энтропии по мере увеличения энергии требует от системы «насыщения» энтропией. Это возможно только в том случае, если число состояний с высокой энергией ограничено. Для системы обычных (квантовых или классических) частиц, таких как атомы или пыль, число состояний с высокой энергией неограниченно (импульсы частиц в принципе можно увеличивать до бесконечности). Однако некоторые системы (см. примеры ниже) обладают максимальным количеством энергии, которое они могут удерживать, и по мере приближения к этой максимальной энергии их энтропия фактически начинает уменьшаться.

История

Возможность отрицательных температур впервые предсказал Ларс Онсагер в 1949 году. Онзагер исследовал двумерные вихри, заключенные в пределах конечной площади, и понял, что, поскольку их положение не является независимыми степенями свободы от их импульсов, результирующее фазовое пространство также должно быть ограничено конечной площадью. Ограниченное фазовое пространство является важным свойством, которое допускает отрицательные температуры и может иметь место как в классических, так и в квантовых системах. Как показал Онзагер, система с ограниченным фазовым пространством обязательно имеет пик энтропии при увеличении энергии. Для энергий, превышающих значение, при котором возникает пик, энтропия уменьшается с увеличением энергии, и состояния с высокой энергией обязательно имеют отрицательную температуру Больцмана.

Ограниченный диапазон состояний, доступных системе с отрицательной температурой, означает, что отрицательная температура связана с возникновением упорядочения системы при высоких энергиях. Например, в точечно-вихревом анализе Онзагера отрицательная температура связана с возникновением крупномасштабных скоплений вихрей. Этот спонтанный порядок в равновесной статистической механике противоречит общепринятой физической интуиции, согласно которой увеличение энергии приводит к увеличению беспорядка.

Кажется, отрицательные температуры были впервые обнаружены экспериментально в 1951 году, когда Перселл и Паунд обнаружили доказательства их существования в ядерных спинах кристалла фторида лития, помещенного в магнитное поле, а затем удаленного из этого поля. Они написали:

Система в состоянии с отрицательной температурой не холодная, а очень горячая, отдавая энергию любой системе с положительной температурой, находящейся с ней в контакте. Он распадается до нормального состояния при бесконечной температуре.

Определение температуры

Шкалу абсолютной температуры (Кельвина) можно условно интерпретировать как среднюю кинетическую энергию частиц системы. Существование отрицательной температуры, не говоря уже о том, что отрицательная температура представляет собой «более горячие» системы, чем положительная температура, в этой интерпретации может показаться парадоксальным. Парадокс разрешается путем рассмотрения более строгого определения термодинамической температуры в терминах формулы энтропии Больцмана . Это показывает компромисс между внутренней энергией и энтропией, содержащейся в системе, при этом « холодность », обратная температуре, является более фундаментальной величиной. В системах с положительной температурой энтропия будет увеличиваться по мере добавления энергии в систему, тогда как в системах с отрицательной температурой энтропия будет уменьшаться по мере добавления энергии в систему.

Определение термодинамической температуры T является функцией изменения энтропии системы S при обратимой передаче тепла Q _rev :

$T={\frac {dQ_{\mathrm {rev} }}{dS}}.$

Поскольку энтропия является функцией состояния , интеграл от dS по любому циклическому процессу равен нулю. Для системы, в которой энтропия является чисто функцией энергии системы E , температуру можно определить как:

$T=\left({\frac {dS}{dE}}\right)^{-1}.$

Аналогично, термодинамическая бета или «холодность» определяется как

$\beta ={\frac {1}{kT}}={\frac {1}{k}}{\frac {dS}{dE}},$

где k — постоянная Больцмана .

Обратите внимание, что в классической термодинамике S определяется через температуру. Здесь все наоборот: S — статистическая энтропия , функция возможных микросостояний системы, а температура передает информацию о распределении энергетических уровней между возможными микросостояниями. Для систем со многими степенями свободы статистические и термодинамические определения энтропии обычно согласуются друг с другом.

Некоторые теоретики предложили использовать альтернативное определение энтропии как способ разрешить предполагаемые несоответствия между статистической и термодинамической энтропией для небольших систем и систем, где количество состояний уменьшается с увеличением энергии, а температуры, полученные из этой энтропии, различны. Утверждалось, что новое определение создаст другие несоответствия; его сторонники утверждают, что это только очевидно.

тепла и

Продолжительность: 44 секунды. 0:44

Когда температура отрицательная, состояния с более высокой энергией будут заняты с большей вероятностью, чем состояния с низкой энергией.

Отрицательные температуры могут существовать только в системе, где существует ограниченное число энергетических состояний (см. ниже). По мере повышения температуры в такой системе частицы переходят во все более высокие энергетические состояния, а по мере повышения температуры число частиц в состояниях с более низкой энергией и в состояниях с более высокой энергией приближается к равенству. (Это следствие определения температуры в статистической механике для систем с ограниченными состояниями.) Правильно вводя энергию в эти системы, можно создать систему, в которой частиц в состояниях с более высокой энергией будет больше, чем частиц. в нижних. Тогда систему можно охарактеризовать как имеющую отрицательную температуру.

Вещество с отрицательной температурой не холоднее абсолютного нуля , а горячее бесконечной температуры. Как выразились Киттель и Кремер (стр. 462):

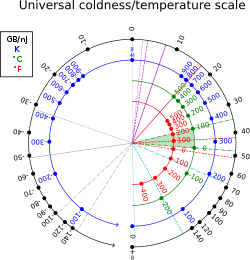
Температурная шкала от холодного до горячего пробега:

:+0 К (-273,15 °С), …, +100 К (-173,15 °С), …, +300 К (+26,85 °С), …, +1000 К (+726,85 °С), …, + ∞ K (+∞ °C), −∞ K (−∞ °C), …, −1000 K (−1273,15 °C), …, −300 K (−573,15 °C), …, −100 K (− 373,15 °С), …, -0 К (-273,15 °С).

Соответствующая обратная температурная шкала для величины β = 1 / kT (где k — постоянная Больцмана ), непрерывно изменяется от низкой энергии к высокой как +∞, …, 0, …, −∞. Поскольку он позволяет избежать резкого скачка от +∞ к −∞, β считается более естественным, чем T . Хотя система может иметь несколько областей отрицательных температур и, следовательно, иметь разрывы от -∞ до +∞.

Во многих известных физических системах температура связана с кинетической энергией атомов. Поскольку не существует верхней границы импульса атома, не существует верхней границы и для числа энергетических состояний, доступных при добавлении большего количества энергии, и, следовательно, нет способа достичь отрицательной температуры. Однако в статистической механике температура может соответствовать другим степеням свободы, а не только кинетической энергии (см. Ниже).

и

Распределение энергии между различными поступательными , колебательными , вращательными , электронными и ядерными модами системы определяет макроскопическую температуру. В «нормальной» системе происходит постоянный обмен тепловой энергией между различными режимами.

Однако в некоторых ситуациях можно изолировать один или несколько режимов. На практике изолированные моды по-прежнему обмениваются энергией с другими модами, но временные рамки этого обмена намного медленнее, чем для обмена внутри изолированной моды. Одним из примеров является случай ядерных спинов в сильном внешнем магнитном поле . В этом случае энергия течет довольно быстро между спиновыми состояниями взаимодействующих атомов, но передача энергии между ядерными спинами и другими модами происходит относительно медленно. Поскольку поток энергии преимущественно происходит внутри спиновой системы, имеет смысл думать о температуре спина, отличной от температуры, связанной с другими модами.

Определение температуры может быть основано на соотношении:

$T={\frac {dq_{\mathrm {rev} }}{dS}}$

Это соотношение предполагает, что положительная температура соответствует состоянию, когда S энтропия увеличивается тепловой энергии q _rev по мере добавления к системе . Это «нормальное» состояние в макроскопическом мире, и оно всегда справедливо для поступательных, колебательных, вращательных и несвязанных со спином электронных и ядерных мод. Причина этого в том, что существует бесконечное количество этих типов мод, и добавление большего количества тепла в систему увеличивает количество энергетически доступных мод и, таким образом, увеличивает энтропию.

Примеры

Невзаимодействующие двухуровневые частицы

Энтропия, термодинамическая бета и температура как функция энергии для системы N невзаимодействующих двухуровневых частиц.

Самый простой пример, хотя и довольно нефизический, — это рассмотреть систему из N частиц, каждая из которых может принимать энергию либо + ε , либо — ε, но в остальном не взаимодействует. Это можно понимать как предел модели Изинга , в котором член взаимодействия становится пренебрежимо малым. Полная энергия системы равна

$E=\varepsilon \sum _{i=1}^{N}\sigma _{i}=\varepsilon j$

где σi _— знак i- й частицы, а j — количество частиц с положительной энергией минус количество частиц с отрицательной энергией . Из элементарной комбинаторики общее количество микросостояний с таким количеством энергии представляет собой биномиальный коэффициент :

$\Omega _{E}={\binom {N}{\frac {N+j}{2}}}={\frac {N!}{\left({\frac {N+j}{2}}\right)!\left({\frac {N-j}{2}}\right)!}}.$

По фундаментальному предположению статистической механики энтропия этого микроканонического ансамбля равна

$S=k_{\text{B}}\ln \Omega _{E}$

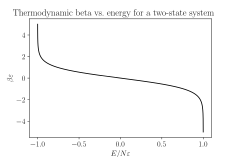
Мы можем найти термодинамическое бета ( β = 1 / k _B T ), рассматривая его как центральную разность без перехода к континуальному пределу :

${\begin{aligned}\beta &={\frac {1}{k_{\mathrm {B} }}}{\frac {\delta _{2\varepsilon }[S]}{2\varepsilon }}\\[3pt]&={\frac {1}{2\varepsilon }}\left(\ln \Omega _{E+\varepsilon }-\ln \Omega _{E-\varepsilon }\right)\\[3pt]&={\frac {1}{2\varepsilon }}\ln \left({\frac {\left({\frac {N+j-1}{2}}\right)!\left({\frac {N-j+1}{2}}\right)!}{\left({\frac {N+j+1}{2}}\right)!\left({\frac {N-j-1}{2}}\right)!}}\right)\\[3pt]&={\frac {1}{2\varepsilon }}\ln \left({\frac {N-j+1}{N+j+1}}\right).\end{aligned}}$

отсюда и температура

$T(E)={\frac {2\varepsilon }{k_{\text{B}}}}\left[\ln \left({\frac {(N+1)\varepsilon -E}{(N+1)\varepsilon +E}}\right)\right]^{-1}.$

Все это доказательство предполагает наличие микроканонического ансамбля с фиксированной энергией и температурой, являющейся эмерджентным свойством. В каноническом ансамбле температура фиксирована, а энергия является эмерджентным свойством. Это приводит к ( ε относится к микросостояниям):

${\begin{aligned}Z(T)&=\sum _{i=1}^{N}e^{-\varepsilon _{i}\beta }\\[6pt]E(T)&={\frac {1}{Z}}\sum _{i=1}^{N}\varepsilon _{i}e^{-\varepsilon _{i}\beta }\\[6pt]S(T)&=k_{\text{B}}\ln(Z)+{\frac {E}{T}}\end{aligned}}$

Следуя предыдущему примеру, мы выбираем состояние с двумя уровнями и двумя частицами. Это приводит к микросостояниям ε ₁ = 0 , ε ₂ = 1 , ε ₃ = 1 и ε ₄ = 2 .

${\begin{aligned}Z(T)&=e^{-0\beta }+2e^{-1\beta }+e^{-2\beta }\\[3pt]&=1+2e^{-\beta }+e^{-2\beta }\\[6pt]E(T)&={\frac {0e^{-0\beta }+2\times 1e^{-1\beta }+2e^{-2\beta }}{Z}}\\[3pt]&={\frac {2e^{-\beta }+2e^{-2\beta }}{Z}}\\[3pt]&={\frac {2e^{-\beta }+2e^{-2\beta }}{1+2e^{-\beta }+e^{-2\beta }}}\\[6pt]S(T)&=k_{\text{B}}\ln \left(1+2e^{-\beta }+e^{-2\beta }\right)+{\frac {2e^{-\beta }+2e^{-2\beta }}{\left(1+2e^{-\beta }+e^{-2\beta }\right)T}}\end{aligned}}$

Полученные значения S , E и Z увеличиваются с ростом T и никогда не требуют перехода в отрицательный температурный режим.

Ядерные спины

Предыдущий пример приближенно реализуется системой ядерных спинов во внешнем магнитном поле. Это позволяет проводить эксперимент как разновидность спектроскопии ядерного магнитного резонанса . В случае электронных и ядерных спиновых систем доступно только конечное число мод, часто всего две, соответствующие спину вверх и спину вниз . В отсутствие магнитного поля эти спиновые состояния вырождены , то есть им соответствует одна и та же энергия. При приложении внешнего магнитного поля уровни энергии расщепляются, поскольку те спиновые состояния, которые выровнены с магнитным полем, будут иметь энергию, отличную от тех, которые антипараллельны ему.

В отсутствие магнитного поля такая двухспиновая система будет иметь максимальную энтропию, когда половина атомов находится в состоянии со спином вверх, а половина — в состоянии со спином вниз, и поэтому можно было бы ожидать найти систему с близкими значениями спина. к равному распределению спинов. При приложении магнитного поля некоторые атомы будут стремиться выстроиться так, чтобы минимизировать энергию системы, поэтому немного больше атомов должно находиться в состоянии с более низкой энергией (для целей этого примера мы предположим, что спин состояние «вниз» — это состояние с более низкой энергией). Добавить энергию в спиновую систему можно с помощью радиочастотных методов. Это заставляет атомы переключаться со спина вниз на спин вверх.

Поскольку мы начали с более половины атомов в состоянии со спином вниз, это первоначально приводит систему к смеси 50/50, поэтому энтропия увеличивается, что соответствует положительной температуре. Однако в какой-то момент более половины вращений оказываются в положении раскрутки вверх. В этом случае добавление дополнительной энергии снижает энтропию, поскольку отдаляет систему от смеси 50/50. Это уменьшение энтропии с добавлением энергии соответствует отрицательной температуре. В ЯМР-спектроскопии это соответствует импульсам с шириной более 180° (для данного спина). Хотя в твердых телах релаксация происходит быстро, в растворах она может занять несколько секунд и даже дольше в газах и ультрахолодных системах; Сообщалось о нескольких часах для серебра и родия при температуре пикокельвина. Еще важно понимать, что температура отрицательна только по отношению к ядерным спинам. Другие степени свободы, такие как молекулярные колебательные, электронные и спиновые уровни электронов, имеют положительную температуру, поэтому объект все еще имеет положительное явное тепло. Релаксация на самом деле происходит за счет обмена энергией между состояниями ядерного спина и другими состояниями (например, посредством ядерного эффекта Оверхаузера с другими спинами).

Лазеры

Это явление также можно наблюдать во многих лазерных системы системах, в которых значительная часть атомов (в химических и газовых лазерах) или электронов (в полупроводниковых лазерах) находится в возбужденном состоянии. Это называется инверсией населенности .

Гамильтониан частоте для одной моды поля люминесцентного излучения на ν равен

$H=(h\nu -\mu )a^{\dagger }a.$

Оператор плотности в большом каноническом ансамбле равен

$\rho ={\frac {e^{-\beta H}}{\operatorname {Tr} \left(e^{-\beta H}\right)}}.$

Чтобы система имела основное состояние, след сходился, а оператор плотности имел общезначимый смысл, βH должен быть положительно полуопределенным. Таким образом, если hν < µ и H отрицательно полуопределено, то β само должно быть отрицательным, что подразумевает отрицательную температуру.

свободы

Отрицательные температуры были также достигнуты в степенях свободы движения . С помощью оптической решетки были установлены верхние границы кинетической энергии, энергии взаимодействия и потенциальной энергии холодных атомов калия-39 . Это было сделано путем настройки взаимодействия атомов с отталкивания на притяжение с использованием резонанса Фешбаха и изменения общего гармонического потенциала с захвата на антизахват, таким образом преобразуя гамильтониан Бозе-Хаббарда из Ĥ → - Ĥ . Выполняя это преобразование адиабатически, сохраняя при этом атомы в изоляторном режиме Мотта , можно перейти из состояния с низкой энтропией с положительной температурой в состояние с низкой энтропией и отрицательной температурой. В состоянии с отрицательной температурой атомы макроскопически занимают состояние с максимальным импульсом решетки. Ансамбли с отрицательной температурой пришли в равновесие и показали длительное время жизни в антизахватывающем гармоническом потенциале.

Двумерное вихревое движение

Двумерные системы вихрей, ограниченные конечной площадью, могут образовывать состояния теплового равновесия при отрицательной температуре: и действительно, состояния с отрицательной температурой были впервые предсказаны Онзагером в его анализе классических точечных вихрей. Предсказание Онзагера было подтверждено экспериментально для системы квантовых вихрей в конденсате Бозе-Эйнштейна в 2019 году.

См. также

• Отрицательное сопротивление

Дальнейшее чтение

• Киттель, К. ; Кремер, Х. (1980). Теплофизика (2-е изд.). У. Х. Фриман . ISBN  978-0-7167-1088-2 .
• Касл, Дж.; Эммерих, В.; Хейкес, Р.; Миллер, Р.; Рейн, Дж. (1965). Наука по градусам: температура от нуля до нуля . Уокер и компания . LCCN   64023985 .
• Браун, С.; Ронцхаймер, JP; Шрайбер, М.; Ходжман, СС; Ром, Т.; Блох, И.; Шнайдер, У. (2013). «Отрицательная абсолютная температура для движущихся степеней свободы» . Наука . 339 (6115): 52–5. arXiv : 1211.0545 . Бибкод : 2013Sci...339...52B . дои : 10.1126/science.1227831 . ПМИД   23288533 . S2CID   8207974 .
• Парихар, В.; Видом, А.; Шривастава, Ю. (2006). «Термические шкалы времени в конденсате цветного стекла». Физический обзор C . 73 (17901): 017901. arXiv : hep-ph/0505199 . Бибкод : 2006PhRvC..73a7901P . дои : 10.1103/PhysRevC.73.017901 . S2CID   119090586 .
• Моск, А. (2005). «Атомные газы при отрицательной кинетической температуре». Письма о физических отзывах . 95 (4): 040403. arXiv : cond-mat/0501344 . Бибкод : 2005PhRvL..95d0403M . doi : 10.1103/PhysRevLett.95.040403 . ПМИД   16090784 . S2CID   1156732 .
• Шмидт, Гарри; Малер, Гюнтер (2005). «Управление локальным релаксационным поведением в закрытых двучастных квантовых системах». Физический обзор E . 72 (7): 016117. arXiv : quant-ph/0502181 . Бибкод : 2005PhRvE..72a6117S . дои : 10.1103/PhysRevE.72.016117 . ПМИД   16090046 . S2CID   17987338 .
• Шен, Цзянь-Ци (2003). «Эффект антиэкранирования и отрицательная температура в мгновенно обращенных электрических полях и левых средах». Физика Скрипта . 68 (1): 87–97. arXiv : cond-mat/0302351 . Бибкод : 2003PhyS...68...87S . doi : 10.1238/Physica.Regular.068a00087 . S2CID   118894011 .
• Кеттерле, Вольфганг (22 сентября 2010 г.). К квантовому магнетизму с ультрахолодными атомами (фильм) . Цюрихский физический коллоквиум . ETH Цюрих, ITS-MMS; Швейцария . Проверено 1 января 2016 г. Отрицательная температура, около 48мин. 53сек.
• Карр, Линкольн Д. (4 января 2013 г.). «Отрицательная температура?». Наука . 339 (6115): 42–43. Бибкод : 2013Sci...339...42C . дои : 10.1126/science.1232558 . ПМИД   23288530 . S2CID   124095369 .

Внешние ссылки

• Мориарти, Филип. «−K: Отрицательные температуры» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .