Необратимый процесс
| Термодинамика |
|---|
 |
В науке процесс , не обратимый, называется необратимым . Это понятие часто возникает в термодинамике . Все сложные природные процессы необратимы. [1] [2] [3] [4] хотя фазовый переход при температуре сосуществования (например, таяние кубиков льда в воде) вполне можно считать обратимым.
В термодинамике изменение термодинамического состояния системы и всего ее окружения не может быть точно восстановлено до исходного состояния бесконечно малыми изменениями какого-либо свойства системы без затрат энергии. Система, в которой происходит необратимый процесс, все еще может вернуться в исходное состояние. Поскольку энтропия является функцией состояния , изменение энтропии системы одинаково независимо от того, является ли процесс обратимым или необратимым. Однако возникает невозможность восстановить среду до ее исходных условий. Необратимый процесс увеличивает общую энтропию системы и ее окружения. Второй закон термодинамики можно использовать, чтобы определить, является ли гипотетический процесс обратимым или нет.
Интуитивно понятно, что процесс обратим, если нет диссипации . Например, расширение Джоуля необратимо, поскольку изначально система неоднородна. Изначально в ней есть часть системы с газом и часть системы без газа. Чтобы произошло рассеивание, должна быть такая неоднородность. Это все равно, как если бы в системе одна часть газа была горячая, а другая холодная. Тогда произойдет рассеяние; Распределение температуры станет равномерным без совершения работы, и это будет необратимо, потому что вы не сможете добавить или удалить тепло или изменить объем, чтобы вернуть систему в исходное состояние. Таким образом, если система всегда однородна, то процесс обратим, а это означает, что вы можете вернуть систему в исходное состояние, добавляя или удаляя тепло, совершая работу над системой или позволяя системе работать. В качестве другого примера, чтобы представить расширение в двигателе внутреннего сгорания как обратимое, мы могли бы предположить, что температура и давление изменяются равномерно по всему объему после искры. Очевидно, что это не так и существует фронт пламени и иногда даже стук в двигателе . Одна из причин, по которой дизельные двигатели способны достигать более высокого КПД, заключается в том, что сгорание происходит гораздо более равномерно, поэтому на рассеяние теряется меньше энергии, и процесс более близок к обратимому. [ нужна ссылка ]
Явление необратимости возникает из-за того, что если термодинамическую систему , то есть любую систему достаточной сложности, взаимодействующих молекул перевести из одного термодинамического состояния в другое, то конфигурация или расположение атомов и молекул в системе изменится в путь, который нелегко предсказать. [5] [6] Некоторая «энергия преобразования» будет использована, поскольку молекулы «рабочего тела» воздействуют друг на друга, когда они переходят из одного состояния в другое. Во время этого преобразования произойдет некоторая потеря или рассеяние тепловой энергии из-за межмолекулярного трения и столкновений. Эта энергия не будет восстановлена, если процесс повернуть вспять.
Многие биологические процессы, которые когда-то считались обратимыми, на самом деле представляют собой пару двух необратимых процессов. Когда-то считалось, что один-единственный фермент катализирует как прямые, так и обратные химические изменения, исследования показали, что обычно необходимы два отдельных фермента схожей структуры, чтобы выполнить то, что приводит к паре термодинамически необратимых процессов. [7]
Абсолютная статистическая обратимость и
В этом разделе есть несколько проблем. Пожалуйста, помогите улучшить его или обсудите эти проблемы на странице обсуждения . ( Узнайте, как и когда удалять эти шаблонные сообщения )
|
Термодинамика определяет статистическое поведение большого числа объектов, точное поведение которых определяется более конкретными законами. Хотя фундаментальные теоретические законы физики обратимы во времени, [8] экспериментально вероятность реальной обратимости мала и прежнее состояние системы и окружения восстанавливается лишь в определенной степени (см.: принцип неопределенности ). Обратимость термодинамики должна носить статистический характер; то есть должно быть просто крайне маловероятно, но не невозможно, что в системе снизится энтропия. Другими словами, обратимость времени выполняется, если процесс происходит так же, как если бы время текло в обратном направлении или порядок состояний в процессе обратный (последнее состояние становится первым и наоборот).
История [ править ]
Немецкий физик Рудольф Клаузиус в 1850-х годах первым математически количественно оценил открытие необратимости в природе, введя понятие энтропии . В своих мемуарах 1854 года «О модифицированной форме второй фундаментальной теоремы механической теории тепла» Клаузиус утверждает:
Более того, может случиться так, что вместо нисходящей передачи тепла, сопровождающей в одном и том же процессе восходящую передачу, может произойти другое постоянное изменение, особенностью которого является то, что оно не является обратимым без того, чтобы оно не было заменено новым постоянным изменением. аналогичного типа или обеспечивающие нисходящую передачу тепла.
Проще говоря, Клаузиус утверждает, что система не может передавать тепло от более холодного тела к более горячему. Например, чашка горячего кофе, помещенная в помещение с комнатной температурой (~ 72 ° F), будет передавать тепло окружающей среде и тем самым охлаждаться, при этом температура в комнате немного повышается (до ~ 72,3 ° F ). Однако та же первоначальная чашка кофе никогда не будет поглощать тепло из окружающей среды, в результате чего она станет еще жарче, а температура в комнате снизится (до ~ 71,7 ° F ). Следовательно, процесс охлаждения кофе необратим, если в систему не будет подведена дополнительная энергия.
Однако при попытке согласовать микроанализ системы с наблюдениями за ее макросостоянием возник парадокс. Многие процессы математически обратимы в своем микросостоянии при анализе с использованием классической механики Ньютона. Этот парадокс явно портит микроскопические объяснения макроскопической тенденции к равновесию, такие как аргумент Джеймса Клерка Максвелла 1860 года о том, что молекулярные столкновения влекут за собой выравнивание температур смешанных газов. [9] С 1872 по 1875 год Людвиг Больцман подкрепил статистическое объяснение этого парадокса в форме формулы энтропии Больцмана , заявив, что увеличение числа возможных микросостояний, в которых может находиться система, увеличит энтропию системы, делая ее менее вероятной. что система вернется в предыдущее состояние. Его формулы количественно выразили анализ, проведенный Уильямом Томсоном, 1-м бароном Кельвином , который утверждал, что: [10] [11]
Уравнения движения в абстрактной динамике совершенно обратимы; любое решение этих уравнений остается действительным, когда переменная времени t заменяется на –t. С другой стороны, физические процессы необратимы: например, трение твердых тел, теплопроводность, диффузия. Тем не менее принцип диссипации энергии совместим с молекулярной теорией, в которой каждая частица подчиняется законам абстрактной динамики.
Другое объяснение необратимых систем было предложено французским математиком Анри Пуанкаре . В 1890 году он опубликовал свое первое объяснение нелинейной динамики, также называемое теорией хаоса . Применяя теорию хаоса ко второму закону термодинамики , парадокс необратимости можно объяснить ошибками, связанными с масштабированием от микросостояний к макросостояниям и степенями свободы, используемыми при проведении экспериментальных наблюдений. Чувствительность к начальным условиям, касающимся системы и ее окружения на микросостоянии, приводит к проявлению необратимых характеристик в наблюдаемой физической сфере. [12]
Примеры необратимых процессов [ править ]
В физической сфере происходит множество необратимых процессов, к которым можно отнести невозможность достижения 100% эффективности передачи энергии. Ниже приводится список спонтанных событий, которые способствуют необратимости процессов. [13]
- Старение (это утверждение оспаривается, поскольку было показано, что старение можно обратить вспять у мышей. [14] НАД+ [15] и теломераза [16] также было продемонстрировано, что они обращают старение вспять.)
- Смерть
- Время
- Теплопередача за счет конечной разницы температур
- Трение
- Пластическая деформация
- Протекание электрического тока через сопротивление
- Намагниченность или поляризация с гистерезисом
- Безудержное расширение жидкостей
- Спонтанные химические реакции
- Самопроизвольное смешивание материи различного состава/состояний.
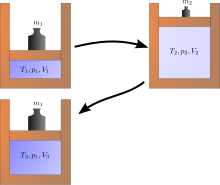
является Расширение Джоуля примером классической термодинамики, поскольку легко вычислить результирующее увеличение энтропии. Это происходит, когда объем газа удерживается на одной стороне термически изолированного контейнера (через небольшую перегородку), а другая сторона контейнера откачивается; Затем перегородка между двумя частями контейнера открывается, и газ заполняет весь контейнер. Внутренняя энергия газа остается прежней, а объем увеличивается. Исходное состояние невозможно восстановить простым сжатием газа до первоначального объема, поскольку при этом сжатии внутренняя энергия увеличится. Исходное состояние можно восстановить только путем охлаждения повторно сжатой системы и тем самым необратимого нагрева окружающей среды. Диаграмма справа применима только в том случае, если первое расширение является «свободным» (расширение Джоуля), т. е. вне цилиндра не может быть атмосферного давления и поднимаемого веса.
Сложные системы [ править ]
Разница между обратимыми и необратимыми событиями имеет особую объяснительную ценность в сложных системах (таких как живые организмы или экосистемы ). По мнению биологов Умберто Матураны и Франсиско Варела , живые организмы характеризуются аутопоэзисом , который обеспечивает их дальнейшее существование. Более примитивные формы самоорганизующихся систем описал физик и химик Илья Пригожин . В контексте сложных систем события, которые приводят к прекращению определенных процессов самоорганизации , таких как смерть , вымирание вида или коллапс метеорологической системы, могут рассматриваться как необратимые. Даже если бы мог быть создан клон с тем же организационным принципом (например, идентичной структурой ДНК), это не означало бы, что прежняя отдельная система снова возродится. События, к которым могут адаптироваться способности к самоорганизации организмов, видов или других сложных систем, такие как незначительные травмы или изменения в физической среде, обратимы. Однако адаптация зависит от импорта негэнтропию в организм, тем самым усиливая необратимые процессы в окружающей его среде. [17] Экологические принципы, такие как принципы устойчивости и принцип предосторожности, можно определить со ссылкой на концепцию обратимости. [18] [19] [20] [21] [22] [23] [5] [24] [25]
См. также [ править ]
Ссылки [ править ]
- ^ Люсия, Ю (1995). «Математические следствия и принцип Дьярмати в рациональной термодинамике». Иль Нуово Чименто . Б110 (10): 1227–1235. Бибкод : 1995NCimB.110.1227L . дои : 10.1007/bf02724612 . S2CID 119568672 .
- ^ Граццини; Люсия, У. (1997). «Глобальный анализ диссипации из-за необратимости». Общий термический обзор . 36 (8): 605–609. дои : 10.1016/s0035-3159(97)89987-4 .
- ^ Люсия, У. (2008). «Вероятность, эргодичность, необратимость и динамические системы». Труды Королевского общества A: Математические, физические и технические науки . 464 (2093): 1089–1104. Бибкод : 2008RSPSA.464.1089L . дои : 10.1098/rspa.2007.0304 . S2CID 34898343 .
- ^ Граццини Дж. и Люсия У., 2008 г. Скорость эволюции термодинамических систем, 1-й международный семинар «Форма и термодинамика» - Флоренция, 25 и 26 сентября 2008 г., стр. 1–7.
- ^ Jump up to: Перейти обратно: а б Люсия, Умберто (октябрь 2009 г.). «Необратимость, энтропия и неполная информация». Физика А: Статистическая механика и ее приложения . 388 (19): 4025–4033. Бибкод : 2009PhyA..388.4025L . дои : 10.1016/j.physa.2009.06.027 .
- ^ Люсия, Ю (2008). «Статистический подход необратимого изменения энтропии». Физика А: Статистическая механика и ее приложения . 387 (14): 3454–3460. Бибкод : 2008PhyA..387.3454L . дои : 10.1016/j.physa.2008.02.002 .
- ^ Люсия У., «Необратимая энтропия в биологических системах», EPISTEME
Люсия, У.; Майно, Г. (2003). «Термодинамический анализ динамики взаимодействия опухоли с иммунной системой хозяина». Физика А: Статистическая механика и ее приложения . 313 (3–4): 569–577. Бибкод : 2002PhyA..313..569L . дои : 10.1016/S0378-4371(02)00980-9 . - ^ Дэвид Альберт о времени и шансе
- ^ Гиенис, Балаж (2017). «Максвелл и нормальное распределение: цветная история вероятности, независимости и тенденции к равновесию». Исследования по истории и философии современной физики . 57 : 53–65. arXiv : 1702.01411 . Бибкод : 2017ШПМП..57...53Г . дои : 10.1016/j.shpsb.2017.01.001 . S2CID 38272381 .
- ^ Бишоп, Колорадо; Бом, А.; Гаделла, М. (2004). «Необратимость в квантовой механике» . Дискретная динамика в природе и обществе . 2004 (1): 75–83. CiteSeerX 10.1.1.576.7850 . дои : 10.1155/S1026022604401046 .
- ^ Лебовиц, Джоэл Л. (1995). «Микроскопическая обратимость и макроскопическое поведение: физические объяснения и математические выводы». 25 лет неравновесной статистической механики . Конспект лекций по физике. Том. 445. стр. 1–20. дои : 10.1007/3-540-59158-3_31 . ISBN 978-3-540-59158-0 . S2CID 16589172 .
- ^ «Второй закон термодинамики» . Страница от 19 февраля 2002 г. Проверено 1 апреля 2010 г.
- ^ Моран, Джон (2008). «Основы технической термодинамики», с. 220. Джон Вили и сыновья, Инк., США. ISBN 978-0-471-78735-8 .
- ^ Ледфорд, Хайди (2 декабря 2020 г.). «Поворот биологических часов восстанавливает зрение у старых мышей». Природа . 588 (7837): 209. Бибкод : 2020Natur.588..209L . дои : 10.1038/d41586-020-03403-0 . PMID 33268879 . S2CID 227259860 .
- ^ Ян, Цун, Лупин; Ло, Сяоянь; Ван, Хуань; Цзинь, Хайся; Ши, Сэнлинь; Повышение уровня НАД+ в яичниках улучшает митохондриальные функции и обращает вспять старение яичников». « Сунь, Инпу (20 августа 2020 г.) . 1–10 . doi : 10.1016/ . 156 j.freeradbiomed.2020.05.003 : S2CID 219312914 .
- ^ Цукалас, Димитрис; Буга, Ана; Дочеа, Анка; Саранди, Евангелия; Митрут, Раду; Реньери, Елизавета; Спандидос, Деметриос; Роговяну, Ион; Серселару, Лилиана; Никулеску, Михаэла; Цацакис, Аристидис; Калина, Даниэла (10 сентября 2021 г.). «Обратное старение мозга путем воздействия на теломеразу: нутрицевтический подход» . Международный журнал молекулярной медицины . 48 (5): 199. doi : 10.3892/ijmm.2021.5032 . ПМЦ 8448543 . ПМИД 34515324 .
- ^ Лонго, Джузеппе; Монтевиль, Маэль (1 января 2012 г.). Диннин, Майкл Дж.; Хусаинов, Бахадыр; Нис, Андре (ред.). Вычисления, физика и не только . Конспекты лекций по информатике. Шпрингер Берлин Гейдельберг. стр. 289–308. CiteSeerX 10.1.1.640.1835 . дои : 10.1007/978-3-642-27654-5_22 . ISBN 9783642276538 . S2CID 16929949 .
- ^ Люсия, Умберто (1998). «Принцип максимума и открытые системы, включающие двухфазные потоки». Revue Generale de Thermique . 37 (9): 813–817. дои : 10.1016/s0035-3159(98)80007-x .
- ^ Люсия У., Необратимость и энтропия в рациональной термодинамике, Ricerche di Matematica, L1 (2001) 77-87.
- ^ Люсия, У.; Джервино, Г. (2005). «Термоэкономический анализ необратимого цикла теплового насоса Стирлинга». Европейский физический журнал Б. 50 (1–2): 367–369. arXiv : физика/0512182 . Бибкод : 2006EPJB...50..367L . дои : 10.1140/epjb/e2006-00060-x . S2CID 119372773 .
- ^ Люсия, Умберто; Майно, Г. (2006). «Релятивистское поведение термодинамического лагранжиана». Иль Нуово Чименто Б. 121 (2): 213–216. Бибкод : 2006NCimB.121..213L . дои : 10.1393/ncb/i2006-10035-8 .
- ^ Люсия, У. (2007). «Необратимое изменение энтропии и проблема тенденции к равновесию». Физика А: Статистическая механика и ее приложения . 376 : 289–292. Бибкод : 2007PhyA..376..289L . дои : 10.1016/j.physa.2006.10.059 .
- ^ Люсия, У.; Джервино, Г. (2009). «Гидродинамика кавитации: от теории к новому экспериментальному подходу» . Центральноевропейский физический журнал . 7 (3): 638–644. Бибкод : 2009CEJPh...7..638L . дои : 10.2478/s11534-009-0092-y . S2CID 120720503 .
- ^ Люсия У., 2009, Термодинамический лагранжиан, в Pandalai SG, 2009, Последние исследовательские разработки в физике, Vol. 8, стр. 1-5, ISBN 978-81-7895-346-5
- ^ Люсия У., 2010, Генерация максимальной энтропии и κ-экспоненциальная модель, Physica A 389, стр. 4558-4563. Люсия, У. (2010). «Поколение максимальной энтропии и κκ-экспоненциальная модель». Физика А: Статистическая механика и ее приложения . 389 (21): 4558–4563. Бибкод : 2010PhyA..389.4558L . дои : 10.1016/j.physa.2010.06.047 .














