завихренность

В механике сплошных сред завихренность — это псевдовекторное (или аксиально-векторное) поле , которое описывает локальное вращательное движение континуума вблизи некоторой точки (тенденция чего-либо вращаться). ), как это увидел бы наблюдатель, находящийся в этой точке и движущийся вместе с потоком . Это важная величина в динамической теории жидкостей вихревых и обеспечивает удобную основу для понимания множества сложных явлений потока, таких как образование и движение колец .

Математически завихренность ${\boldsymbol {\omega }}$ - ротор потока скорости $\mathbf {v}$:

${\boldsymbol {\omega }}\equiv \nabla \times \mathbf {v} \,,$

где $\nabla$это оператор набла . Концептуально, ${\boldsymbol {\omega }}$можно определить, отмечая части континуума в небольшой окрестности рассматриваемой точки и наблюдая за их относительными смещениями по мере движения вдоль потока. завихренность ${\boldsymbol {\omega }}$будет в два раза больше среднего вектора угловой скорости этих частиц относительно их центра масс , ориентированного в соответствии с правилом правой руки . По своему определению вектор завихренности является соленоидальным полем, поскольку $\nabla \cdot {\boldsymbol {\omega }}=0.$

В двумерном потоке ${\boldsymbol {\omega }}$ всегда перпендикулярно плоскости потока и поэтому может считаться скалярным полем .

Математическое определение и свойства

Математически завихренность трехмерного потока представляет собой псевдовекторное поле, обычно обозначаемое ${\boldsymbol {\omega }}$, определяемый как ротор поля скорости $\mathbf {v}$описывающее непрерывное движение. В декартовых координатах :

${\begin{aligned}{\boldsymbol {\omega }}=\nabla \times \mathbf {v} =\left({\dfrac {\partial v_{z}}{\partial y}}-{\dfrac {\partial v_{y}}{\partial z}},{\dfrac {\partial v_{x}}{\partial z}}-{\dfrac {\partial v_{z}}{\partial x}},{\dfrac {\partial v_{y}}{\partial x}}-{\dfrac {\partial v_{x}}{\partial y}}\right)\,.\end{aligned}}$

Другими словами, завихренность показывает, как изменяется вектор скорости при движении на бесконечно малое расстояние в направлении, перпендикулярном ему.

В двумерном потоке, где скорость не зависит от $z$-координатный и не имеет $z$-компонента, вектор завихренности всегда параллелен $z$-ось и, следовательно, может быть выражено как скалярное поле, умноженное на постоянный единичный вектор. ${\hat {z}}$:

${\begin{aligned}{\boldsymbol {\omega }}=\nabla \times \mathbf {v} =\left({\frac {\partial v_{y}}{\partial x}}-{\frac {\partial v_{x}}{\partial y}}\right)\mathbf {e} _{z}\,.\end{aligned}}$

потока Завихренность также связана с циркуляцией (линейный интеграл скорости) по замкнутому пути согласно (классической) теореме Стокса . А именно, для любого бесконечно малого элемента поверхности C с направлением нормали $\mathbf {n}$ и площадь $dA$, тираж $d\Gamma$ по периметру ​ $C$ это скалярное произведение ${\boldsymbol {\omega }}\cdot (\mathbf {n} \,dA)$ где ${\boldsymbol {\omega }}$ это завихренность в центре $C$.

Поскольку завихренность является аксиальным вектором, ей можно сопоставить антисимметричный тензор второго порядка ${\boldsymbol {\Omega }}$ (так называемый тензор завихренности или вращения), который называется двойственным ${\boldsymbol {\omega }}$. Связь между двумя величинами в индексных обозначениях определяется выражением

$\Omega _{ij}=\varepsilon _{ijk}\omega _{k},\qquad \omega _{i}={\frac {1}{2}}\varepsilon _{ijk}\Omega _{jk}$

где $\varepsilon _{ijk}$— трехмерный тензор Леви-Чивита . Тензор завихренности — это просто антисимметричная часть тензора $\nabla \mathbf {v}$, то есть,

${\boldsymbol {\Omega }}={\frac {1}{2}}\left[\nabla \mathbf {v} -(\nabla \mathbf {v} )^{T}\right]\quad {\text{or}}\quad \Omega _{ij}={\frac {1}{2}}\left({\frac {\partial v_{i}}{\partial x_{j}}}-{\frac {\partial v_{i}}{\partial x_{i}}}\right).$

Примеры

В массе континуума, вращающейся как твердое тело, завихренность в два раза превышает вектор угловой скорости этого вращения. Так обстоит дело, например, в центральном ядре вихря Ренкина .

Завихренность может быть отличной от нуля, даже когда все частицы текут по прямым и параллельным траекториям , если есть сдвиг (то есть, если скорость потока меняется поперек линий тока ). Например, при ламинарном потоке внутри трубы постоянного сечения все частицы движутся параллельно оси трубы; но быстрее вблизи этой оси и практически неподвижен у стен. Завихренность будет равна нулю на оси и максимальной вблизи стенок, где сдвиг наибольший.

И наоборот, поток может иметь нулевую завихренность, даже если его частицы движутся по искривленным траекториям. Примером является идеальный безвихревой вихрь , в котором большинство частиц вращаются вокруг некоторой прямой оси со скоростью, обратно пропорциональной их расстоянию до этой оси. Небольшой участок континуума, который не пересекает ось, будет вращаться в одном направлении, но сдвигаться в противоположном, так что их средняя угловая скорость вокруг центра масс будет равна нулю.

Примеры потоков:
Вихрь, похожий на твердое тело в ∝ р	Параллельный поток со сдвигом	Безвихревой вихрь v ∝ 1 / р
где v — скорость потока, r — расстояние до центра вихря, а ∝ указывает на пропорциональность . Абсолютные скорости вокруг выделенной точки: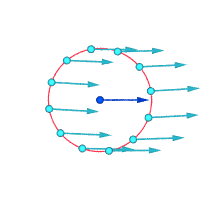
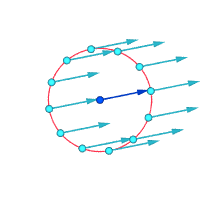
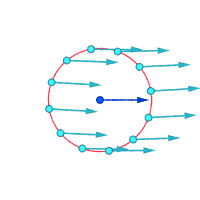
Относительные скорости (увеличенные) вокруг выделенной точки.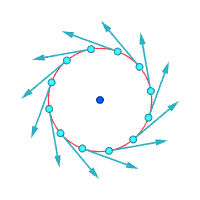
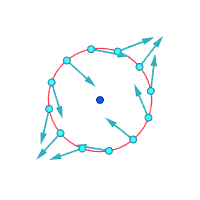
Завихренность ≠ 0	Завихренность ≠ 0	Завихренность = 0

Другой способ визуализировать завихрение — представить, что крошечная часть континуума мгновенно становится твердой, а остальная часть потока исчезает. Если эта крошечная новая твердая частица вращается, а не просто движется вместе с потоком, то в потоке возникает завихренность. На рисунке ниже левый подрисунок демонстрирует отсутствие завихренности, а правый подрисунок демонстрирует наличие завихренности.

Эволюция

Эволюция поля завихренности во времени описывается уравнением завихренности , которое можно вывести из уравнений Навье–Стокса .

Во многих реальных течениях, где вязкостью можно пренебречь (точнее, в течениях с большим числом Рейнольдса ), поле завихренности можно моделировать совокупностью дискретных вихрей, причем завихренность пренебрежимо мала всюду, кроме небольших областей пространства, окружающих оси вихри. Это верно в случае двумерного потенциального потока (т.е. двумерного потока с нулевой вязкостью), и в этом случае поле потока можно смоделировать как комплексное поле на комплексной плоскости .

Завихренность полезна для понимания того, как идеальные потенциальные решения потока могут быть искажены для моделирования реальных потоков. В общем, наличие вязкости вызывает диффузию завихренности от ядер вихрей в общее поле течения; этот поток объясняется диффузионным членом в уравнении переноса завихренности.

Вихревые линии и вихревые трубки

Вихревая линия или линия завихрения — это линия, всюду касающаяся локального вектора завихренности. Вихревые линии определяются соотношением

${\frac {dx}{\omega _{x}}}={\frac {dy}{\omega _{y}}}={\frac {dz}{\omega _{z}}}\,,$

где ${\boldsymbol {\omega }}=(\omega _{x},\omega _{y},\omega _{z})$ – вектор завихренности в декартовых координатах .

Вихревая трубка — это поверхность в континууме, образованная всеми вихревыми линиями, проходящими через заданную (приводимую) замкнутую кривую в континууме. «Сила» вихревой трубки (также называемая вихревым потоком ) представляет собой интеграл завихренности по поперечному сечению трубки и одинаков повсюду вдоль трубки (поскольку завихренность имеет нулевую дивергенцию). Следствием теорем Гельмгольца (или, что то же самое, теоремы Кельвина о циркуляции ) является то, что в невязкой жидкости «сила» вихревой трубы также постоянна во времени. Эффекты вязкости приводят к потерям на трение и зависимости от времени.

В трехмерном потоке завихренность (измеряемая объемным интегралом от квадрата ее величины) может усиливаться при удлинении вихревой линии — явление, известное как растяжение вихря . Это явление происходит при образовании вихря в вытекающей воде и образовании торнадо восходящими потоками воздуха.

Измерители завихренности

Лопастной вихревой измеритель

Лопастной вихремер изобрел русский инженер-гидротехник А.Я. Милович (1874–1958). В 1913 году он предложил пробку с четырьмя прикрепленными к ней лопастями как устройство, качественно показывающее величину вертикальной проекции завихренности, и продемонстрировал киносъемку движения поплавка по поверхности воды на модели излучины реки.

Измерители завихренности с вращающимися лопастями обычно показывают в учебных фильмах по механике сплошной среды (известные примеры включают фильм NCFMF «Завихренность»). и «Фундаментальные принципы потока» Института гидравлических исследований Айовы. ).

Конкретные науки

Воздухоплавание

В аэродинамике распределение подъемной силы по конечному крылу можно аппроксимировать, предполагая, что за каждым сегментом крыла по размаху стоит полубесконечный вихрь. Тогда можно определить силу вихрей, используя критерий отсутствия потока через поверхность крыла. Эта процедура называется методом вихревой панели вычислительной гидродинамики . Затем силы вихрей суммируются, чтобы найти общую приблизительную циркуляцию вокруг крыла. Согласно теореме Кутты-Жуковского , подъемная сила на единицу пролета является произведением циркуляции, воздушной скорости и плотности воздуха.

Науки об атмосфере

Относительная завихренность — это завихренность относительно Земли, вызванная полем скорости воздуха. Это поле скорости воздуха часто моделируется как двумерный поток, параллельный земле, так что вектор относительной завихренности обычно представляет собой скалярную величину вращения, перпендикулярную земле. Завихренность положительна, когда, глядя на поверхность Земли, ветер поворачивает против часовой стрелки. В северном полушарии положительная завихренность называется циклоническим вращением , а отрицательная завихренность — антициклоническим вращением ; в Южном полушарии номенклатура меняется на противоположную.

Абсолютная завихренность рассчитывается на основе скорости воздуха относительно инерциальной системы отсчета и, следовательно, включает в себя член, связанный с вращением Земли, параметр Кориолиса .

Потенциальная завихренность — это абсолютная завихренность, деленная на вертикальное расстояние между уровнями постоянной (потенциальной) температуры (или энтропии ). Абсолютная завихренность воздушной массы изменится, если воздушную массу растянуть (или сжать) в вертикальном направлении, но потенциальная завихренность сохраняется в адиабатическом потоке . Поскольку в атмосфере преобладает адиабатический поток, потенциальная завихренность полезна в качестве приблизительного индикатора воздушных масс в атмосфере в течение нескольких дней, особенно если рассматривать ее на уровнях постоянной энтропии.

Уравнение баротропной завихренности — это самый простой способ прогнозирования движения волн Россби (то есть впадин и хребтов 500 гПа с геопотенциальной высотой ) в течение ограниченного периода времени (несколько дней). В 1950-х годах это уравнение использовалось в первых успешных программах численного прогнозирования погоды .

В современных моделях численного прогноза погоды и моделях общей циркуляции (МОЦ) завихренность может быть одной из прогнозируемых переменных, и в этом случае соответствующее зависящее от времени уравнение является прогностическим уравнением .

С концепцией завихренности связана спиральность. $H(t)$, определяется как

$H(t)=\int _{V}\mathbf {v} \cdot {\boldsymbol {\omega }}\,dV$

где интеграл ведется по заданному объему $V$. В науке об атмосфере спиральность движения воздуха важна для прогнозирования суперячейок и потенциальной торнадо- активности.

См. также

• Уравнение баротропной завихренности
• Парадокс Даламбера
• Энстрофия
• Палинстрофия
• Потенциал скорости
• Вихрь
• Вихревая трубка
• Вихревое растяжение
• Подковообразный вихрь
• Вихри на законцовках крыльев

Гидродинамика

• Закон Био – Савара
• Тираж
• Уравнения завихренности
• Теорема Кутты – Жуковского

Науки об атмосфере

• Прогностическое уравнение
• Карл-Густав Россби
• Ганс Эртель

Библиография

• Ачесон, диджей (1990). Элементарная гидродинамика . Издательство Оксфордского университета. ISBN  0-19-859679-0 .
• Ландау, Л.Д.; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN  978-0-08-057073-0 .
• Позрикидис, К. (2011). Введение в теоретическую и вычислительную гидродинамику . Издательство Оксфордского университета. ISBN  978-0-19-975207-2 .
• Гийон, Этьен; Юлен, Жан-Пьер; Пети, Люк; Митеску, Каталин Д. (2001). Физическая гидродинамика . Издательство Оксфордского университета. ISBN  0-19-851746-7 .
• Бэтчелор, Г.К. (2000) [1967], Введение в гидродинамику , издательство Кембриджского университета, ISBN  0-521-66396-2
• Клэнси, LJ (1975), Аэродинамика , Pitman Publishing Limited, Лондон ISBN   0-273-01120-0
• « Погодный глоссарий » The Weather Channel Interactive, Inc., 2004 г.
• « Завихренность ». Интегрированное издательство.

Дальнейшее чтение

• Окитани, К., « Элементарный учет завихренности и родственные уравнения ». Издательство Кембриджского университета. 30 января 2005 г. ISBN   0-521-81984-9
• Хорен, Александр Ж. , « Завихренность и турбулентность ». Прикладные математические науки, том 103, Springer-Verlag. 1 марта 1994 года. ISBN   0-387-94197-5
• Майда, Эндрю Дж. , Андреа Л. Бертоцци, « Завихренность и несжимаемый поток ». Издательство Кембриджского университета; 2002. ISBN   0-521-63948-4
• Триттон, DJ , « Физическая гидродинамика ». Ван Ностранд Рейнхольд, Нью-Йорк. 1977. ISBN   0-19-854493-6
• Арфкен Г. « Математические методы для физиков », 3-е изд. Academic Press, Орландо, Флорида. 1985. ISBN   0-12-059820-5

Внешние ссылки

• Вайсштейн, Эрик В., « Завихрение ». Scienceworld.wolfram.com.
• Досвелл III, Чарльз А., « Букварь по завихренности для применения в суперячейках и торнадо ». Кооперативный институт мезомасштабных метеорологических исследований, Норман, Оклахома.
• Крамер, М.С., « Уравнения Навье – Стокса. Теоремы переноса завихренности : Введение ». Основы механики жидкости.
• Паркер, Дуглас, « ENVI 2210 – Динамика атмосферы и океана, 9: Завихрение ». Школа окружающей среды Университета Лидса. Сентябрь 2001 года.
• Грэм, Джеймс Р. , « Астрономия 202: Астрофизическая газовая динамика ». Астрономический факультет Калифорнийского университета в Беркли .
  • « Уравнение завихренности: несжимаемая и баротропная жидкости ».
  • « Интерпретация уравнения завихренности ».
  • « Теорема Кельвина о завихренности для несжимаемого или баротропного течения ».
• « Сферпак 3.1 ». (включает в себя набор программ vorticity FORTRAN)
• « Мезомасштабное сжимаемое сообщество (МС2) Прогнозы модели в реальном времени ». (Анализ потенциального завихрения)