Контактные механики

Напряжения в зоне контакта действуют одновременно под действием нормальной и касательной силы. Напряжения стали видимыми с помощью фотоупругости .

Контактная механика – это изучение деформации твердых , тел соприкасающихся друг с другом в одной или нескольких точках. Основное различие в механике контакта заключается в напряжениях, действующих перпендикулярно поверхностям контактирующих тел (известных как нормальное напряжение ), и трения, напряжениях действующих по касательной между поверхностями ( напряжение сдвига ). Механика нормального контакта или механика контакта без трения фокусируется на нормальных напряжениях, вызванных приложенными нормальными силами и адгезией, присутствующей на поверхностях, находящихся в тесном контакте, даже если они чистые и сухие. Механика фрикционного контакта подчеркивает влияние сил трения.

Контактная механика является частью машиностроения . Физико-математическая формулировка предмета основана на механике материалов и механике сплошных сред и фокусируется на расчетах с участием упругих , вязкоупругих и пластических тел, находящихся в статическом или динамическом контакте. Контактная механика дает необходимую информацию для безопасного и энергоэффективного проектирования технических систем, а также для изучения трибологии , контактной жесткости , электрического контактного сопротивления и твердости при вдавливании . Принципы контактной механики применяются в таких приложениях, как контакт колеса локомотива с рельсом, сцепные устройства, тормозные системы, шины , подшипники , двигатели внутреннего сгорания , механические соединения , уплотнительные прокладки, металлообработка , формовка металлов, ультразвуковая сварка , электрические контакты и многие другие. Текущие проблемы, с которыми сталкиваются в этой области, могут включать анализ напряжений контактных и соединительных элементов, а также влияние смазки и конструкции материала на трение и износ . Применение контактной механики распространяется и на микро- и нанотехнологическая сфера.

Оригинальные работы по контактной механике относятся к 1881 году с публикацией статьи «О контакте упругих тел». ( «Ueber die Berührung fester elastischer Körper» ) Генриха Герца . Герц пытался понять, как оптические свойства нескольких сложенных друг на друга линз могут меняться в зависимости от силы, удерживающей их вместе. Контактное напряжение Герца относится к локализованным напряжениям, которые возникают, когда две изогнутые поверхности вступают в контакт и слегка деформируются под действием приложенных нагрузок. Эта величина деформации зависит от модуля упругости контактирующего материала. Он дает контактное напряжение как функцию нормальной контактной силы, радиусов кривизны обоих тел и модуля упругости обоих тел. Контактное напряжение Герца лежит в основе уравнений несущей способности и усталостной долговечности в подшипниках, зубчатых передачах и любых других телах, где две поверхности находятся в контакте.

История

Когда сфера прижимается к упругому материалу, площадь контакта увеличивается.

Классическая контактная механика прежде всего связана с Генрихом Герцем. В 1882 году Герц решил задачу о контакте двух упругих тел с искривленными поверхностями. Это до сих пор актуальное классическое решение обеспечивает основу для современных задач контактной механики. Например, в машиностроении и трибологии представляет контактное напряжение Герца собой описание напряжения внутри сопрягаемых деталей. Контактное напряжение Герца обычно относится к напряжению, близкому к области контакта между двумя сферами разных радиусов.

Лишь почти сто лет спустя Джонсон , Кендалл и Робертс нашли аналогичное решение для случая адгезионного контакта. Эта теория была отвергнута Борисом Дерягиным и сотрудниками. который предложил другую теорию адгезии в 1970-е годы. Модель Дерягина стала известна как модель ДМТ (по имени Дерягина, Мюллера и Топорова). и Джонсон и др. Модель стала известна как модель JKR (в честь Джонсона, Кендалла и Робертса) для адгезионно-эластичного контакта. Этот отказ сыграл важную роль в развитии Табора. и позже Могис параметры, которые количественно определяют, какая модель контакта (из моделей JKR и DMT) лучше представляет адгезионный контакт с конкретными материалами.

Дальнейший прогресс в области контактной механики в середине двадцатого века можно отнести к таким именам, как Боуден и Табор . Боуден и Тейбор были первыми, кто подчеркнул важность шероховатости поверхности контактирующих тел. При исследовании шероховатости поверхности установлено, что истинная площадь контакта между партнерами трения меньше кажущейся площади контакта. Такое понимание коренным образом изменило и направление работ в трибологии. Работы Боудена и Табора породили несколько теорий контактной механики шероховатых поверхностей.

Вклад Арчарда (1957) Следует также упомянуть при обсуждении новаторских работ в этой области. Арчард пришел к выводу, что даже для шероховатых упругих поверхностей площадь контакта примерно пропорциональна нормальной силе . Дальнейшие важные выводы в этом направлении были сделаны Гринвудом и Уильямсоном (1966): Буш (1975), и Перссон (2002). Основные выводы этих работ заключались в том, что истинная поверхность контакта в шероховатых материалах обычно пропорциональна нормальной силе, в то время как параметры отдельных микроконтактов (т. е. давление, размер микроконтакта) лишь слабо зависят от нагрузки. .

Классические решения для неклейкого эластичного контакта

Теорию контакта между упругими телами можно использовать для определения площадей контакта и глубины отпечатков для простых геометрических форм. Ниже перечислены некоторые часто используемые решения. Теория, используемая для вычисления этих решений, обсуждается далее в статье. Решения для множества других технически важных форм, например, усеченного конуса, изношенной сферы, грубых профилей, полых цилиндров и т. д. можно найти в

Контакт сферы с полупространством

Контакт упругой сферы с упругим полупространством

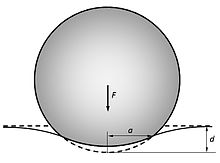
Упругая сфера радиуса ​ $R$ вдавливает упругое полупространство , где общая деформация равна $d$, в результате чего площадь контакта радиусом

$a={\sqrt {Rd}}$

Приложенная сила $F$ связано со смещением $d$ к

$F={\frac {4}{3}}E^{*}R^{\frac {1}{2}}d^{\frac {3}{2}}$

где

${\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}$

и $E_{1}$, $E_{2}$ – модули упругости и $\nu _{1}$, $\nu _{2}$ связанные коэффициенты Пуассона, с каждым телом.

Распределение нормального давления в зоне контакта в зависимости от расстояния от центра круга:

$p(r)=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}$

где $p_{0}$ максимальное контактное давление, определяемое формулой

$p_{0}={\frac {3F}{2\pi a^{2}}}={\frac {1}{\pi }}\left({\frac {6F{E^{*}}^{2}}{R^{2}}}\right)^{\frac {1}{3}}$

Радиус круга зависит от приложенной нагрузки. $F$ по уравнению

$a^{3}={\cfrac {3FR}{4E^{*}}}$

Общая деформация $d$ связано с максимальным контактным давлением соотношением

$d={\frac {a^{2}}{R}}=\left({\frac {9F^{2}}{16{E^{*}}^{2}R}}\right)^{\frac {1}{3}}$

Максимальное касательное напряжение возникает внутри при $z\approx 0.49a$ для $\nu =0.33$.

Контакт двух сфер

Контакт между двумя сферами.

Контакт двух скрещенных цилиндров одинакового радиуса.

Для контакта двух сфер радиусов $R_{1}$ и $R_{2}$, область контакта представляет собой круг радиуса $a$. Уравнения те же, что и для сферы, контактирующей с полуплоскостью, за исключением того, что эффективный радиус $R$ определяется как

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

Контакт между двумя скрещенными цилиндрами одинакового радиуса

Это эквивалентно контакту сферы радиуса $R$ и самолет .

полупространством

Контакт жесткого цилиндрического индентора с упругим полупространством.

Если жесткий цилиндр вдавить в упругое полупространство, создается распределение давления, описываемое формулой

$p(r)=p_{0}\left(1-{\frac {r^{2}}{R^{2}}}\right)^{-{\frac {1}{2}}}$

где $R$ - радиус цилиндра и

$p_{0}={\frac {1}{\pi }}E^{*}{\frac {d}{R}}$

Связь между глубиной вдавливания и нормальной силой определяется выражением

$F=2RE^{*}d$

полупространством

Контакт жесткого конического индентора с упругим полупространством.

В случае вдавливания упругого полупространства модуля Юнга $E$ при использовании жесткого конического индентора глубина области контакта $\epsilon$ и радиус контакта $a$ связаны

$\epsilon =a\tan(\theta )$

с $\theta$ определяется как угол между плоскостью и боковой поверхностью конуса. Общая глубина вдавливания $d$ дается:

$d={\frac {\pi }{2}}\epsilon$

Полная сила

$F={\frac {\pi E}{2\left(1-\nu ^{2}\right)}}a^{2}\tan(\theta )={\frac {2E}{\pi \left(1-\nu ^{2}\right)}}{\frac {d^{2}}{\tan(\theta )}}$

Распределение давления определяется выражением

$p\left(r\right)={\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}\ln \left({\frac {a}{r}}+{\sqrt {\left({\frac {a}{r}}\right)^{2}-1}}\right)={\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}\cosh ^{-1}\left({\frac {a}{r}}\right)$

напряжение имеет логарифмическую особенность На вершине конуса .

Контакт между двумя цилиндрами с параллельными осями

Контакт между двумя цилиндрами с параллельными осями

При контакте двух цилиндров с параллельными осями сила линейно пропорциональна длине цилиндров L и глубине вдавливания d :

$F\approx {\frac {\pi }{4}}E^{*}Ld$

Радиусы кривизны в этом соотношении полностью отсутствуют. Радиус контакта описывается обычным соотношением

$a={\sqrt {Rd}}$

с

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

как в контакте между двумя сферами. Максимальное давление равно

$p_{0}=\left({\frac {E^{*}F}{\pi LR}}\right)^{\frac {1}{2}}$

Контакт подшипника

Основная статья: Давление подшипника

Контакт в случае подшипников часто представляет собой контакт между выпуклой поверхностью (охватывающий цилиндр или сфера) и вогнутой поверхностью (охватывающий цилиндр или сфера: отверстие или полусферическая чашка ).

Метод

Контакт сферы с упругим полупространством и одномерная замененная модель.

Некоторые контактные проблемы можно решить с помощью метода уменьшения размерности (МДР). В этом методе исходная трехмерная система заменяется контактом тела с линейно-упругим или вязкоупругим основанием (см. рис.). Свойства одномерных систем в точности совпадают со свойствами исходной трехмерной системы, если видоизменить форму тел и определить элементы основания по правилам МДР. MDR основан на решении осесимметричных контактных задач, впервые полученных Людвигом Фёпплем (1941) и Герхардом Шубертом (1942).

Однако для получения точных аналитических результатов необходимо, чтобы контактная задача была осесимметричной и контакты были компактными.

неадгезионного упругого

Классическая теория контакта фокусировалась главным образом на неадгезивном контакте, при котором в зоне контакта не допускается возникновение силы натяжения, т. е. контактирующие тела могут быть разделены без сил сцепления. Для решения контактных задач, удовлетворяющих условию отсутствия адгезии, использовалось несколько аналитических и численных подходов. сложные силы и моменты Между телами в местах их соприкосновения передаются , поэтому задачи контактной механики могут стать весьма сложными. Кроме того, контактные напряжения обычно являются нелинейной функцией деформации. Для упрощения процедуры решения обычно определяют систему отсчета , в которой объекты (возможно, движущиеся относительно друг друга) статичны. Они взаимодействуют посредством поверхностного натяжения (или давления/напряжения) на границе раздела.

В качестве примера рассмотрим два объекта, которые встречаются на некоторой поверхности. $S$ в ( $x$, $y$)-плоскость с $z$-ось предполагается нормальной к поверхности. Одно из тел испытает нормально направленное давления . распределение $p_{z}=p(x,y)=q_{z}(x,y)$ в плоскости тяги на поверхности и распределение $q_{x}=q_{x}(x,y)$ и $q_{y}=q_{y}(x,y)$ по региону $S$. С точки зрения баланса сил Ньютона , силы:

$P_{z}=\int _{S}p(x,y)~\mathrm {d} A~;~~Q_{x}=\int _{S}q_{x}(x,y)~\mathrm {d} A~;~~Q_{y}=\int _{S}q_{y}(x,y)~\mathrm {d} A$

должны быть равны и противоположны силам, установленным в другом теле. Моменты, соответствующие этим силам:

$M_{x}=\int _{S}y~q_{z}(x,y)~\mathrm {d} A~;~~M_{y}=\int _{S}-x~q_{z}(x,y)~\mathrm {d} A~;~~M_{z}=\int _{S}[x~q_{y}(x,y)-y~q_{x}(x,y)]~\mathrm {d} A$

также необходимо соединить тела так, чтобы они были кинематически неподвижны.

теории

При определении решений контактных задач Герца принимаются следующие предположения :

• Деформации малы и находятся в пределах упругости.
• Поверхности непрерывны и несогласны (подразумевается, что площадь контакта намного меньше характерных размеров контактирующих тел).
• Каждое тело можно рассматривать как упругое полупространство.
• Поверхности не подвержены трению.

Дополнительные сложности возникают, когда некоторые или все эти предположения нарушаются, и такие контактные задачи обычно называют негерцевыми .

Методы аналитического решения

Контакт между двумя сферами.

Аналитические методы решения задачи неклейкого контакта можно разделить на два типа в зависимости от геометрии области контакта. Соответствующий контакт — это контакт, при котором два тела соприкасаются в нескольких точках до того, как произойдет какая-либо деформация (т. е. они просто «прилегают друг к другу»). Несоответствующий контакт — это контакт, при котором формы тел настолько различаются, что при нулевой нагрузке они соприкасаются только в одной точке (или, возможно, вдоль линии). В несоответствующем случае площадь контакта мала по сравнению с размерами объектов и напряжения сильно концентрируются в этой области. Такой контакт называется концентрированным , иначе его называют диверсифицированным .

Распространенный подход в области линейной упругости заключается в наложении ряда решений, каждое из которых соответствует точечной нагрузке, действующей на область контакта. Например, в случае нагружения полуплоскости решение Фламанта часто используется в качестве отправной точки, а затем обобщается на различные формы области контакта. Балансы сил и моментов между двумя контактирующими телами действуют как дополнительные ограничения для решения.

Точечный контакт на (2D) полуплоскости

Основная статья: Решение Фламинго

Схема нагружения плоскости силой P в точке (0, 0).

Отправной точкой для решения контактных задач является понимание эффекта «точечной нагрузки», приложенной к изотропной, однородной и линейно упругой полуплоскости, показанной на рисунке справа. Проблема может заключаться либо в плоском напряжении , либо в плоской деформации . Это краевая задача линейной упругости с учетом тяговых граничных условий :

$\sigma _{xz}(x,0)=0~;~~\sigma _{z}(x,z)=-P\delta (x,z)$

где $\delta (x,z)$ – дельта-функция Дирака . Граничные условия гласят, что на поверхности нет касательных напряжений и в точке (0, 0) приложена сингулярная нормальная сила P. Применение этих условий к основным уравнениям упругости дает результат

${\begin{aligned}\sigma _{xx}&=-{\frac {2P}{\pi }}{\frac {x^{2}z}{\left(x^{2}+z^{2}\right)^{2}}}\\\sigma _{zz}&=-{\frac {2P}{\pi }}{\frac {z^{3}}{\left(x^{2}+z^{2}\right)^{2}}}\\\sigma _{xz}&=-{\frac {2P}{\pi }}{\frac {xz^{2}}{\left(x^{2}+z^{2}\right)^{2}}}\end{aligned}}$

в какой-то момент, $(x,y)$, в полуплоскости. Круг, показанный на рисунке, указывает на поверхность, на которой максимальное напряжение сдвига является постоянным. По этому полю напряжений можно определить компоненты деформации и, таким образом, перемещения всех материальных точек.

Линейный контакт на (2D) полуплоскости

Нормальная загрузка по региону

Предположим, что вместо точечной нагрузки $P$, распределенная нагрузка $p(x)$ вместо этого применяется к поверхности в диапазоне $a<x<b$. Принцип линейной суперпозиции можно применить для определения результирующего поля напряжений как решения интегральных уравнений:

${\begin{aligned}\sigma _{xx}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(x-x'\right)^{2}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{3}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {p\left(x'\right)\left(x-x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\end{aligned}}$

Сдвиговая нагрузка в регионе

Тот же принцип применим и к нагрузке на поверхность в плоскости поверхности. Подобные тяги обычно возникают в результате трения. Решение аналогично приведенному выше (для обеих единичных нагрузок $Q$ и распределенные нагрузки $q(x)$), но немного изменено:

${\begin{aligned}\sigma _{xx}&=-{\frac {2}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)^{3}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}~;~~\sigma _{zz}=-{\frac {2z^{2}}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\\[3pt]\sigma _{xz}&=-{\frac {2z}{\pi }}\int _{a}^{b}{\frac {q\left(x'\right)\left(x-x'\right)^{2}\,dx'}{\left[\left(x-x'\right)^{2}+z^{2}\right]^{2}}}\end{aligned}}$

Эти результаты сами по себе могут быть наложены на результаты, приведенные выше для нормальной нагрузки, чтобы иметь дело с более сложными нагрузками.

Точечный контакт на (3D) полупространстве

Аналогично решению Фламанта для двумерной полуплоскости фундаментальные решения известны и для линейно упругого трехмерного полупространства. Они были найдены Буссинеском для сосредоточенной нормальной нагрузки и Черрути для тангенциальной нагрузки. См. раздел об этом в разделе «Линейная эластичность» .

решения

Нет необходимости проводить различия между соответствующим и несоответствующим контактом, когда для решения контактных задач используются схемы численного решения. Эти методы не полагаются на дальнейшие предположения в процессе решения, поскольку они основаны исключительно на общей формулировке основных уравнений. Помимо стандартных уравнений, описывающих деформацию и движение тел, можно сформулировать еще два неравенства. Первый просто ограничивает движение и деформацию тел, полагая, что проникновение произойти не может. Отсюда и разрыв $h$ между двумя телами может быть только положительным или нулевым

$h\geq 0$

где $h=0$ обозначает контакт. Второе допущение в контактной механике связано с тем, что в зоне контакта не допускается возникновение сил натяжения (соприкасающиеся тела могут подниматься вверх без сил сцепления). Это приводит к неравенству, которому должны подчиняться напряжения на контактной границе. Он разработан для нормального стресса. $\sigma _{n}=\mathbf {t} \cdot \mathbf {n}$.

В местах соприкосновения поверхностей зазор равен нулю, т.е. $h=0$, и там нормальное напряжение отлично от нуля, действительно, $\sigma _{n}<0$. В местах, где поверхности не соприкасаются, нормальное напряжение равно нулю; $\sigma _{n}=0$, при этом разрыв положителен; то есть, $h>0$. Этот тип формулировки дополнительности может быть выражен в так называемой форме Куна – Такера , а именно.

$h\geq 0\,,\quad \sigma _{n}\leq 0\,,\quad \sigma _{n}\,h=0\,.$

Эти условия справедливы в общем смысле. Математическая формулировка разрыва зависит от кинематики базовой теории твердого тела (например, линейного или нелинейного твердого тела в двух или трех измерениях, балки или оболочки модели ). Повторяя обычный стресс $\sigma _{n}$ по контактному давлению, $p$; то есть, $p=-\sigma _{n}$ проблему Куна-Такера можно переформулировать в стандартной форме дополнительности, т.е.

$$h\geq 0\,,\quad p\geq 0\,,\quad p\,h=0\,.$$

В линейно-упругом случае зазор можно сформулировать как

$${h}=h_{0}+{g}+u,$$

где $h_{0}$- разделение твердого тела, $g$ — геометрия/топография контакта (цилиндр и шероховатость) и $u$ – упругая деформация/прогиб. Если контактирующие тела аппроксимируются как линейные упругие полупространства, для выражения деформации можно применить решение интегрального уравнения Буссинеска-Черрути ( $u$) в зависимости от контактного давления ( $p$); то есть,

$$u=\int _{\infty }^{\infty }K(x-s)p(s)ds,$$

где

$$K(x-s)={\frac {2}{\pi E^{*}}}\ln |x-s|$$

для линейной загрузки упругого полупространства и

$$K(x-s)={\frac {1}{\pi E^{*}}}{\frac {1}{\sqrt {\left(x_{1}-s_{1}\right)^{2}+\left(x_{2}-s_{2}\right)^{2}}}}$$

для точечного нагружения упругого полупространства.

После дискретизации задача механики линейного упругого контакта может быть сформулирована в стандартной форме линейной задачи дополнительности (LCP).

${\begin{aligned}\mathbf {h} &=\mathbf {h} _{0}+\mathbf {g} +\mathbf {Cp} ,\\\mathbf {h} \cdot \mathbf {p} &=0,\,\,\,\mathbf {p} \geq 0,\,\,\,\mathbf {h} \geq 0,\\\end{aligned}}$

где $\mathbf {C}$ представляет собой матрицу, элементами которой являются так называемые коэффициенты влияния, связывающие контактное давление и деформацию. Строгая формулировка LCP задачи CM, представленная выше, позволяет напрямую применять хорошо зарекомендовавшие себя методы численного решения, такие как алгоритм поворота Лемке . Преимущество алгоритма Лемке заключается в том, что он находит численно точное решение за конечное число итераций. Реализация MATLAB, представленная Almqvist et al. Это один из примеров, который можно использовать для численного решения проблемы. Кроме того, пример кода для решения LCP двумерной задачи механики линейного упругого контакта также был опубликован на обмене файлами MATLAB Альмквистом и др.

Контакт между шероховатыми поверхностями

Когда два тела с шероховатыми поверхностями прижимаются друг к другу, истинная площадь контакта, образующаяся между двумя телами, равна $A$, намного меньше, чем кажущаяся или номинальная площадь контакта $A_{0}$. Механика контакта шероховатых поверхностей обсуждается с точки зрения механики нормального контакта и статического фрикционного взаимодействия. Естественные и инженерные поверхности обычно демонстрируют особенности шероховатости, известные как неровности, в широком диапазоне масштабов длины вплоть до молекулярного уровня, при этом поверхностные структуры демонстрируют самородство, также известное как поверхностная фрактальность . Признано, что самоаффинная структура поверхностей является причиной линейного масштабирования истинной площади контакта с приложенным давлением. Если предположить модель сдвига сварных контактов при трибологических взаимодействиях, то эту повсеместно наблюдаемую линейность между площадью контакта и давлением можно также считать источником линейности зависимости между статическим трением и приложенной нормальной силой.

При контакте между «случайной шероховатой» поверхностью и упругим полупространством истинная площадь контакта связана с нормальной силой. $F$ к

$A={\frac {\kappa }{E^{*}h'}}F$

с $h'$ равный среднеквадратичному (также известному как среднее квадратичное) наклона поверхности и $\kappa \approx 2$ . Среднее давление на истинной контактной поверхности

$p_{\mathrm {av} }={\frac {F}{A}}\approx {\frac {1}{2}}E^{*}h'$

можно разумно оценить как половину эффективного модуля упругости $E^{*}$ умножается на среднеквадратичный уклон поверхности $h'$ .

Обзор модели GW

Гринвуд и Уильямсон в 1966 году (GW) предложил теорию упруго-контактной механики шероховатых поверхностей, которая сегодня является основой многих теорий трибологии (трения, адгезии, тепло- и электропроводности, износа и др.). Они рассматривали контакт между гладкой жесткой плоскостью и номинально плоской деформируемой шероховатой поверхностью, покрытой закругленными выступами того же радиуса R. Их теория предполагает, что деформация каждой неровности не зависит от деформации ее соседей и описывается моделью Герца. . Высоты неровностей имеют случайное распределение. Вероятность того, что высота неровности находится между $z$ и $z+dz$ является $\phi (z)dz$. Авторы подсчитали количество пятен контакта n, общую площадь контакта $A_{r}$ и общая нагрузка P в общем случае. Они дали эти формулы в двух формах: в базовой и с использованием стандартизированных переменных. Если предположить, что N неровностей покрывают шероховатую поверхность, то ожидаемое количество контактов составит

$n=N\int _{d}^{\infty }\phi (z)dz$

Ожидаемую общую площадь контакта можно рассчитать по формуле

$A_{a}=N\pi R\int _{d}^{\infty }(z-d)\phi (z)dz$

а ожидаемая общая сила определяется выражением

$P={\frac {4}{3}}NE_{r}{\sqrt {R}}\int _{d}^{\infty }(z-d)^{\frac {3}{2}}\phi (z)dz$

где:

R — радиус кривизны микронеровности,

z — высота микронеровности, отсчитываемая от линии профиля,

d, закрыть поверхность,

$E_{r}=\left({\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}\right)^{-1}$, составной модуль упругости Юнга,

$E_{i}$, модуль упругости поверхности,

$\nu _{i}$, коэффициенты поверхности Пуассона.

Гринвуд и Уильямсон представили стандартизированное разделение $h=d/\sigma$ и стандартизированное распределение высоты $\phi ^{*}(s)$ стандартное отклонение которого равно единице. Ниже представлены формулы в стандартизированном виде.

${\begin{aligned}F_{n}(h)&=\int _{h}^{\infty }(s-h)^{n}\phi ^{*}(s)ds\\n&=\eta A_{n}F_{0}(h)\\A_{a}&=\pi \eta AR\sigma F_{1}(h)\\P&={\frac {4}{3}}\eta AE_{r}{\sqrt {R}}\sigma ^{\frac {3}{2}}F_{\frac {3}{2}}(h)\end{aligned}}$

где:

d — разделение,

$A$ номинальная площадь контакта,

$\eta$ – поверхностная плотность неровностей,

$E^{*}$ – эффективный модуль Юнга.

$A$ и $P$ можно определить, когда $F_{n}(h)$ члены рассчитываются для заданных поверхностей с использованием свертки шероховатости поверхности $\phi ^{*}(s)$. В нескольких исследованиях применялись предложенные аппроксимации кривой для $F_{n}(h)$ предполагая высокое распределение поверхности по Гауссу с подгонкой кривой, представленной Arcoumanis et al. и Единак среди других. Неоднократно наблюдалось, что инженерные поверхности не демонстрируют гауссово распределение высоты поверхности, например, Пекленика. Лейтон и др. представлены посадки для заштрихованных поверхностей гильз цилиндров двигателя внутреннего сгорания, а также процесс определения $F_{n}(h)$ Условия для любых измеряемых поверхностей. Лейтон и др. продемонстрировал, что данные по Гауссу неточны для моделирования любых инженерных поверхностей, и продолжил демонстрировать раннее притирание поверхностей приводит к постепенному переходу, который существенно меняет топографию поверхности, несущую способность и трение.

В последнее время точные аппроксимации $A_{r}$ и $P$ были опубликованы издательством «Единак». Они задаются следующими рациональными формулами, являющимися аппроксимациями интегралов $F_{n}(h)$. Они рассчитываются для гауссова распределения неровностей, которое, как было показано, нереально для инженерной поверхности, но может быть принято в тех случаях, когда результаты трения, несущей способности или реальной площади контакта не имеют решающего значения для анализа.

$F_{n}(h)={\frac {a_{0}+a_{1}h+a_{2}h^{2}+a_{3}h^{3}}{1+b_{1}h+b_{2}h^{2}+b_{3}h^{3}+b_{4}h^{4}+b_{5}h^{5}+b_{6}h^{6}}}\exp \left(-{\frac {h^{2}}{2}}\right)$

Для $F_{1}(h)$ коэффициенты

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.398942280401,0.159773702775,0.0389687688311,0.00364356495452]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=\left[1.653807476138,1.170419428529,0.448892964428,0.0951971709160,0.00931642803836,-6.383774657279\times 10^{-6}\right]\end{aligned}}$

Максимальная относительная погрешность $9.93\times 10^{-8}\%$.

Для $F_{\frac {3}{2}}(h)$ коэффициенты

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.430019993662,0.101979509447,0.0229040629580,0.000688602924]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.671117125984,1.199586555505,0.46936532151,0.102632881122,0.010686348714,0.0000517200271]\end{aligned}}$

Максимальная относительная погрешность $1.91\times 10^{-7}\%$. Бумага также содержит точные выражения для $F_{n}(h)$

${\begin{aligned}F_{1}(h)&={\frac {1}{\sqrt {2\pi }}}\exp \left(-{\frac {1}{2}}h^{2}\right)-{\frac {1}{2}}h\,\operatorname {erfc} \left({\frac {h}{\sqrt {2}}}\right)\\F_{\frac {3}{2}}(h)&={\frac {1}{4{\sqrt {\pi }}}}\exp \left(-{\frac {h^{2}}{4}}\right){\sqrt {h}}\left(\left(h^{2}+1\right)K_{\frac {1}{4}}\left({\frac {h^{2}}{4}}\right)-h^{2}K_{\frac {3}{4}}\left({\frac {h^{2}}{4}}\right)\right)\end{aligned}}$

где erfc(z) означает дополнительную функцию ошибок, а $K_{\nu }(z)$ – модифицированная функция Бесселя второго рода.

Для ситуации, когда неровности на двух поверхностях имеют гауссово распределение высоты и пики можно считать сферическими, среднее контактное давление достаточно, чтобы вызвать текучесть, когда $p_{\text{av}}=1.1\sigma _{y}\approx 0.39\sigma _{0}$ где $\sigma _{y}$ - одноосный предел текучести и $\sigma _{0}$ это твердость отпечатка. Гринвуд и Уильямсон определил безразмерный параметр $\Psi$ называется индексом пластичности , который можно использовать для определения того, будет ли контакт упругим или пластичным.

Модель Гринвуда-Вильямсона требует знания двух статистически зависимых величин; стандартное отклонение шероховатости поверхности и кривизны пиков неровностей. Альтернативное определение индекса пластичности было дано Микичем. Текучесть возникает, когда давление превышает одноосный предел текучести. Поскольку предел текучести пропорционален твердости при вдавливании $\sigma _{0}$Микич определил индекс пластичности упругопластического контакта как

$\Psi ={\frac {E^{*}h'}{\sigma _{0}}}>{\frac {2}{3}}~.$

В этом определении $\Psi$ представляет собой микрошероховатость в состоянии полной пластичности, и необходима только одна статистическая величина - среднеквадратичный наклон, который можно рассчитать на основе измерений поверхности. Для $\Psi <{\frac {2}{3}}$, поверхность при контакте ведет себя упруго.

В обеих моделях Гринвуда-Вильямсона и Микика предполагается, что нагрузка пропорциональна деформируемой площади. Следовательно, будет ли система вести себя пластично или упруго, не зависит от приложенной нормальной силы.

Обзор модели GT

Модель, предложенная Гринвудом и Триппом (GT), расширил модель GW для контакта между двумя шероховатыми поверхностями. Модель GT широко используется в области эластогидродинамического анализа.

Наиболее часто цитируемые уравнения модели GT относятся к площади контакта неровностей.

$A_{a}=\pi ^{2}(\eta \beta \sigma )^{2}AF_{2}(\lambda ),$

и нагрузка, переносимая неровностями

$P={\frac {8{\sqrt {2}}}{15}}\pi (\eta \beta \sigma )^{2}{\sqrt {\frac {\sigma }{\beta }}}E'AF_{\frac {5}{2}}(\lambda ),$

где:

$\eta \beta \sigma$, параметр шероховатости,

$A$, номинальная площадь контакта,

$\lambda$, параметр масляной пленки Штрибека, впервые определенный Стрибеком \cite{gt} как $\lambda =h/\sigma$,

$E'$, эффективный модуль упругости,

$F_{2},F_{\frac {5}{2}}(\lambda )$, статистические функции, введенные для соответствия предполагаемому гауссовскому распределению неровностей.

Лейтон и др. представлены посадки для заштрихованных поверхностей гильз цилиндров двигателя внутреннего сгорания, а также процесс определения $F_{n}(h)$ Условия для любых измеряемых поверхностей. Лейтон и др. продемонстрировал, что данные по Гауссу неточны для моделирования любых инженерных поверхностей, и продолжил демонстрировать раннее притирание поверхностей приводит к постепенному переходу, который существенно меняет топографию поверхности, несущую способность и трение.

Точные решения для $A_{a}$ и $P$ впервые представлены Джединаком. Они выражаются $F_{n}$ следующее. Они рассчитываются для гауссова распределения неровностей, которое, как было показано, нереально для инженерной поверхности, но может быть принято в тех случаях, когда результаты трения, несущей способности или реальной площади контакта не имеют решающего значения для анализа.

${\begin{aligned}F_{2}&={\frac {1}{2}}\left(h^{2}+1\right)\operatorname {erfc} \left({\frac {h}{\sqrt {2}}}\right)-{\frac {h}{\sqrt {2\pi }}}\exp \left(-{\frac {h^{2}}{2}}\right)\\F_{\frac {5}{2}}&={\frac {1}{8{\sqrt {\pi }}}}\exp \left(-{\frac {h^{2}}{4}}\right)h^{\frac {3}{2}}\left(\left(2h^{2}+3\right)K_{\frac {3}{4}}\left({\frac {h^{2}}{4}}\right)-\left(2h^{2}+5\right)K_{\frac {1}{4}}\left({\frac {h^{2}}{4}}\right)\right)\end{aligned}}$

где erfc(z) означает дополнительную функцию ошибок, а $K_{\nu }(z)$ – модифицированная функция Бесселя второго рода.

В бумаге можно найти подробный обзор существующих аппроксимаций $F_{\frac {5}{2}}$. Новые предложения дают наиболее точные аппроксимации $F_{\frac {5}{2}}$ и $F_{2}$, о которых сообщается в литературе. Они задаются следующими рациональными формулами, которые являются очень точными аппроксимациями интегралов $F_{n}(h)$. Они рассчитаны для гауссова распределения неровностей

$F_{n}(h)={\frac {a_{0}+a_{1}h+a_{2}h^{2}+a_{3}h^{3}}{1+b_{1}h+b_{2}h^{2}+b_{3}h^{3}+b_{4}h^{4}+b_{5}h^{5}+b_{6}h^{6}}}\exp \left(-{\frac {h^{2}}{2}}\right)$

Для $F_{2}(h)$ коэффициенты

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.5,0.182536384941,0.039812283118,0.003684879001]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.960841785003,1.708677456715,0.856592986083,0.264996791567,0.049257843893,0.004640740133]\end{aligned}}$

Максимальная относительная погрешность $1.68\times 10^{-7}\%$.

Для $F_{\frac {5}{2}}(h)$ коэффициенты

${\begin{aligned}[][a_{0},a_{1},a_{2},a_{3}]&=[0.616634218997,0.108855827811,0.023453835635,0.000449332509]\\[][b_{1},b_{2},b_{3},b_{4},b_{5},b_{6}]&=[1.919948267476,1.635304362591,0.799392556572,0.240278859212,0.043178653945,0.003863334276]\end{aligned}}$

Максимальная относительная погрешность $4.98\times 10^{-8}\%$.

Клеевой контакт между упругими телами

Когда две твердые поверхности находятся в непосредственной близости, на них действуют силы притяжения Ван-дер-Ваальса . Модель Ван дер Ваальса Брэдли. обеспечивает средство расчета растягивающей силы между двумя твердыми сферами с идеально гладкими поверхностями. Модель контакта Герца не считает возможной адгезию. Однако в конце 1960-х годов при сравнении теории Герца с экспериментами по контакту между резиновыми и стеклянными сферами наблюдалось несколько противоречий.

Было замечено что, хотя теория Герца применима при больших нагрузках, при малых нагрузках

• площадь контакта была больше, чем предсказывала теория Герца,
• площадь контакта имела ненулевое значение даже при снятой нагрузке, и
• сильная адгезия наблюдалась даже в том случае, если контактирующие поверхности были чистыми и сухими.

Это указывало на то, что действуют силы сцепления. Модель Джонсона-Кендалла-Робертса (JKR) и модель Дерягина-Мюллера-Топорова (DMT) были первыми, кто включил адгезию в контакт Герца.

контакта

Принято считать, что поверхностная сила между двумя атомными плоскостями, находящимися на расстоянии $z$ друг от друга могут быть получены из потенциала Леннарда-Джонса . С этим предположением

$F(z)={\cfrac {16\gamma }{3z_{0}}}\left[\left({\cfrac {z}{z_{0}}}\right)^{-9}-\left({\cfrac {z}{z_{0}}}\right)^{-3}\right]$

где $F$ - сила (положительная при сжатии), $2\gamma$ - общая поверхностная энергия обеих поверхностей на единицу площади, а $z_{0}$ представляет собой равновесное разделение двух атомных плоскостей.

Модель Брэдли применила потенциал Леннарда-Джонса, чтобы найти силу сцепления между двумя твердыми сферами. Суммарная сила между сферами равна

$F_{a}(z)={\cfrac {16\gamma \pi R}{3}}\left[{\cfrac {1}{4}}\left({\cfrac {z}{z_{0}}}\right)^{-8}-\left({\cfrac {z}{z_{0}}}\right)^{-2}\right]~;~~{\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}$

где $R_{1},R_{2}$ - радиусы двух сфер.

Две сферы полностью разделяются, когда сила отрыва достигает $z=z_{0}$ в какой момент

$F_{a}=F_{c}=-4\gamma \pi R.$

Модель упругого контакта Джонсона-Кендалла-Робертса

Схема контактной площадки модели JKR.

JKR-тест с жестким валиком на деформируемом плоском материале: полный цикл

Чтобы включить эффект адгезии в контакт по Герцу, Джонсон, Кендалл и Робертс сформулировал теорию адгезионного контакта JKR, используя баланс между запасенной упругой энергией и потерей поверхностной энергии . Модель JKR учитывает влияние контактного давления и адгезии только внутри области контакта. Общее решение для распределения давления в зоне контакта в модели JKR имеет вид

$p(r)=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}+p_{0}'\left(1-{\frac {r^{2}}{a^{2}}}\right)^{-{\frac {1}{2}}}$

Обратите внимание, что в исходной теории Герца член, содержащий $p_{0}'$ было проигнорировано на том основании, что напряжение в зоне контакта поддерживать невозможно. Для контакта между двумя сферами

$p_{0}={\frac {2aE^{*}}{\pi R}};\quad p_{0}'=-\left({\frac {4\gamma E^{*}}{\pi a}}\right)^{\frac {1}{2}}$

где $a\,$ - радиус области контакта, $F$ это приложенная сила, $2\gamma$ - общая поверхностная энергия обеих поверхностей на единицу площади контакта, $R_{i},\,E_{i},\,\nu _{i},~~i=1,2$ - радиусы, модули Юнга и коэффициенты Пуассона двух сфер, и

${\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}};\quad {\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}$

Расстояние сближения между двумя сферами определяется выражением

$d={\frac {\pi a}{2E^{*}}}\left(p_{0}+2p_{0}'\right)={\frac {a^{2}}{R}}$

Уравнение Герца для площади контакта двух сфер, модифицированное с учетом поверхностной энергии, имеет вид

$a^{3}={\frac {3R}{4E^{*}}}\left(F+6\gamma \pi R+{\sqrt {12\gamma \pi RF+(6\gamma \pi R)^{2}}}\right)$

Когда поверхностная энергия равна нулю, $\gamma =0$, уравнение Герца для контакта двух сфер восстановлено. Когда приложенная нагрузка равна нулю, радиус контакта равен

$a^{3}={\frac {9R^{2}\gamma \pi }{E^{*}}}$

Растягивающая нагрузка, при которой сферы разделяются (т. е. $a=0$), по прогнозам, будет

$F_{\text{c}}=-3\gamma \pi R\,$

Эту силу еще называют силой отрыва . Обратите внимание, что эта сила не зависит от модулей двух сфер. Однако существует и другое возможное решение для значения $a$ при этой нагрузке. Это критическая зона контакта. $a_{\text{c}}$, заданный

$a_{\text{c}}^{3}={\frac {9R^{2}\gamma \pi }{4E^{*}}}$

Если определить работу адгезии как

$\Delta \gamma =\gamma _{1}+\gamma _{2}-\gamma _{12}$

где $\gamma _{1},\gamma _{2}$ - энергии сцепления двух поверхностей и $\gamma _{12}$ является членом взаимодействия, мы можем записать радиус контакта JKR как

$a^{3}={\frac {3R}{4E^{*}}}\left(F+3\Delta \gamma \pi R+{\sqrt {6\Delta \gamma \pi RF+(3\Delta \gamma \pi R)^{2}}}\right)$

Растягивающая нагрузка при отрыве равна

$F=-{\frac {3}{2}}\Delta \gamma \pi R\,$

а критический радиус контакта определяется выражением

$a_{\text{c}}^{3}={\frac {9R^{2}\Delta \gamma \pi }{8E^{*}}}$

Критическая глубина проникновения равна

$d_{\text{c}}={\frac {a_{c}^{2}}{R}}=\left(R^{\frac {1}{2}}{\frac {9\Delta \gamma \pi }{4E^{*}}}\right)^{\frac {2}{3}}$

Derjaguin-Muller-Toporov (DMT) model of elastic contact

The Derjaguin-Muller-Toporov (DMT) model представляет собой альтернативную модель адгезионного контакта, которая предполагает, что профиль контакта остается таким же, как при контакте Герца, но с дополнительными притягивающими взаимодействиями за пределами области контакта.

Радиус контакта между двумя сферами из теории ДМТ равен

$a^{3}={\cfrac {3R}{4E^{*}}}\left(F+4\gamma \pi R\right)$

и сила отрыва

$F_{c}=-4\gamma \pi R\,$

При достижении силы отрыва площадь контакта становится равной нулю и сингулярность контактных напряжений на краю площадки контакта отсутствует.

По работе адгезии $\Delta \gamma$

$a^{3}={\cfrac {3R}{4E^{*}}}\left(F+2\Delta \gamma \pi R\right)$

и

$F_{c}=-2\Delta \gamma \pi R\,$

Параметр Табора

В 1977 году Табор показал, что кажущееся противоречие между теориями JKR и DMT можно разрешить, отметив, что эти две теории представляют собой крайние пределы единой теории, параметризованной параметром Табора ( $\mu$) определяется как

$\mu :={\frac {d_{c}}{z_{0}}}\approx \left[{\frac {R(\Delta \gamma )^{2}}{{E^{*}}^{2}z_{0}^{3}}}\right]^{\frac {1}{3}}$

где $z_{0}$ равновесное расстояние между двумя контактирующими поверхностями. Теория JKR применима к крупным, податливым сферам, в которых $\mu$ большой. Теория ДМТ применима к маленьким жестким сферам с небольшими значениями $\mu$.

Впоследствии Дерягин и его сотрудники применив закон поверхностной силы Брэдли к упругому полупространству, подтвердил, что с увеличением параметра Табора сила отрыва падает по сравнению со значением Брэдли. $2\pi R\Delta \gamma$ к стоимости JKR $(3/2)\pi R\Delta \gamma$. Более подробные расчеты позже были проведены Гринвудом. демонстрирует S-образную кривую нагрузки/подхода, которая объясняет эффект прыжка. Более эффективный метод вычислений и дополнительные результаты были предоставлены Фэном.

контакта Можиса

Схема области контакта для модели Можиса-Дугдейла.

Дальнейшее усовершенствование идеи Табора было предложено Можисом. который представил поверхностную силу в терминах аппроксимации зоны сцепления Дагдейла , так что работа адгезии определяется выражением

$\Delta \gamma =\sigma _{0}~h_{0}$

где $\sigma _{0}$ это максимальная сила, предсказанная потенциалом Леннарда-Джонса и $h_{0}$ — максимальное разделение, полученное путем сопоставления площадей под кривыми Дагдейла и Леннарда-Джонса (см. соседний рисунок). Это означает, что сила притяжения постоянна для $z_{0}\leq z\leq z_{0}+h_{0}$. Дальнейшего проникновения при сжатии нет. Идеальный контакт происходит в области радиуса $a$ и силы сцепления величиной $\sigma _{0}$ распространяться на область радиуса $c>a$. В этом регионе $a<r<c$, две поверхности разделены расстоянием $h(r)$ с $h(a)=0$ и $h(c)=h_{0}$. Соотношение $m$ определяется как

$m:={\frac {c}{a}}$.

В теории Можиса-Дугдейла Распределение поверхностного сцепления разделено на две части — одну из-за контактного давления Герца, а другую — из-за адгезионного напряжения Дагдейла. Предполагается контакт Герца в области $-a<r<a$. Вклад в поверхностное сцепление давления Герца определяется выражением

$p^{H}(r)=\left({\frac {3F^{H}}{2\pi a^{2}}}\right)\left(1-{\frac {r^{2}}{a^{2}}}\right)^{\frac {1}{2}}$

где контактная сила Герца $F^{H}$ дается

$F^{H}={\frac {4E^{*}a^{3}}{3R}}$

Проникновение за счет упругого сжатия

$d^{H}={\frac {a^{2}}{R}}$

Вертикальное смещение при $r=c$ является

$u^{H}(c)={\cfrac {1}{\pi R}}\left[a^{2}\left(2-m^{2}\right)\sin ^{-1}\left({\frac {1}{m}}\right)+a^{2}{\sqrt {m^{2}-1}}\right]$

и расстояние между двумя поверхностями в $r=c$ является

$h^{H}(c)={\frac {c^{2}}{2R}}-d^{H}+u^{H}(c)$

Распределение поверхностного сцепления из-за адгезионного напряжения Дагдейла равно

$p^{D}(r)={\begin{cases}-{\frac {\sigma _{0}}{\pi }}\cos ^{-1}\left[{\frac {2-m^{2}-{\frac {r^{2}}{a^{2}}}}{m^{2}\left(1-{\frac {r^{2}}{m^{2}a^{2}}}\right)}}\right]&\quad {\text{for}}\quad r\leq a\\-\sigma _{0}&\quad {\text{for}}\quad a\leq r\leq c\end{cases}}$

Тогда общая сила сцепления определяется выражением

$F^{D}=-2\sigma _{0}m^{2}a^{2}\left[\cos ^{-1}\left({\frac {1}{m}}\right)+{\frac {1}{m^{2}}}{\sqrt {m^{2}-1}}\right]$

Сжатие, обусловленное адгезией Дагдейла, равно

$d^{D}=-\left({\frac {2\sigma _{0}a}{E^{*}}}\right){\sqrt {m^{2}-1}}$

и разрыв в $r=c$ является

$h^{D}(c)=\left({\frac {4\sigma _{0}a}{\pi E^{*}}}\right)\left[{\sqrt {m^{2}-1}}\cos ^{-1}\left({\frac {1}{m}}\right)+1-m\right]$

Тогда чистая тяга на площади контакта определяется выражением $p(r)=p^{H}(r)+p^{D}(r)$ а чистая контактная сила равна $F=F^{H}+F^{D}$. Когда $h(c)=h^{H}(c)+h^{D}(c)=h_{0}$ адгезионная тяга падает до нуля.

Безразмерные значения $a,c,F,d$ на этом этапе вводятся, которые игнорируются как

${\bar {a}}=\alpha a~;~~{\bar {c}}:=\alpha c~;~~{\bar {d}}:=\alpha ^{2}Rd~;~~\alpha :=\left({\frac {4E^{*}}{3\pi \Delta \gamma R^{2}}}\right)^{\frac {1}{3}}~;~~{\bar {A}}:=\pi c^{2}~;~~{\bar {F}}={\frac {F}{\pi \Delta \gamma R}}$

Кроме того, Могис предложил параметр $\lambda$ что эквивалентно параметру Табора $\mu$ . Этот параметр определяется как

$\lambda :=\sigma _{0}\left({\frac {9R}{2\pi \Delta \gamma {E^{*}}^{2}}}\right)^{\frac {1}{3}}\approx 1.16\mu$

где шаг когезионного напряжения $\sigma _{0}$ равно теоретическому напряжению потенциала Леннарда-Джонса

$\sigma _{\text{th}}={\frac {16\Delta \gamma }{9{\sqrt {3}}z_{0}}}$

Чжэн и Ю предложил другое значение для ступенчатого когезионного напряжения.

$\sigma _{0}=\exp \left(-{\frac {223}{420}}\right)\cdot {\frac {\Delta \gamma }{z_{0}}}\approx 0.588{\frac {\Delta \gamma }{z_{0}}}$

соответствовать потенциалу Леннарда-Джонса, что приводит к

$\lambda \approx 0.663\mu$

Тогда результирующую контактную силу можно выразить как

${\bar {F}}={\bar {a}}^{3}-\lambda {\bar {a}}^{2}\left[{\sqrt {m^{2}-1}}+m^{2}\sec ^{-1}m\right]$

и упругое сжатие как

${\bar {d}}={\bar {a}}^{2}-{\frac {4}{3}}~\lambda {\bar {a}}{\sqrt {m^{2}-1}}$

Уравнение когезионного зазора между двумя телами принимает вид

${\frac {\lambda {\bar {a}}^{2}}{2}}\left[\left(m^{2}-2\right)\sec ^{-1}m+{\sqrt {m^{2}-1}}\right]+{\frac {4\lambda {\bar {a}}}{3}}\left[{\sqrt {m^{2}-1}}\sec ^{-1}m-m+1\right]=1$

Это уравнение можно решить, чтобы получить значения $c$ для различных значений $a$ и $\lambda$. Для больших значений $\lambda$, $m\rightarrow 1$ и получается модель JKR. Для небольших значений $\lambda$ модель DMT получена.

Модель Карпика-Оглтри-Салмерона (COS)

Модель Можиса-Дагдейла может быть решена итеративно только в том случае, если значение $\lambda$ заранее неизвестно. Приближенное решение Карпика-Оглтри-Салмерона. упрощает процесс, используя следующее соотношение для определения радиуса контакта $a$:

$a=a_{0}(\beta )\left({\frac {\beta +{\sqrt {1-F/F_{c}(\beta )}}}{1+\beta }}\right)^{\frac {2}{3}}$

где $a_{0}$ - площадь контакта при нулевой нагрузке, а $\beta$ это параметр перехода, который связан с $\lambda$ к

$\lambda \approx -0.924\ln(1-1.02\beta )$

Дело $\beta =1$ точно соответствует теории JKR, а $\beta =0$ соответствует теории ДМТ. Для промежуточных случаев $0<\beta <1$ модель COS близко соответствует решению Можиса-Дугдейла для $0.1<\lambda <5$.

Влияние формы контакта

Даже при наличии идеально гладких поверхностей может проявиться геометрия в виде макроскопической формы контактирующей области. При осторожном отрывании жесткого пуансона с плоской, но необычной формы поверхностью от мягкого аналога его отрыв происходит не мгновенно, а фронты отрыва начинаются от заостренных углов и продвигаются внутрь, пока не будет достигнута конечная конфигурация, которая для макроскопически изотропных форм почти круглая. Основным параметром, определяющим адгезионную прочность плоских контактов, является максимальный линейный размер контакта. Процесс отслоения можно наблюдать экспериментально, можно увидеть в фильме.

См. также

• Клей – неметаллический материал, используемый для склеивания различных материалов.
• Клеевое соединение - техника соединения, используемая при производстве и ремонте.
• Адгезионная железная дорога - железная дорога, использующая сцепление для движения поездов.
• Поверхностные силы адгезии . Молекулярные свойства.
• Несущая способность – способность почвы выдерживать нагрузки.
• Столкновение – случай, когда два или более тел физически контактируют друг с другом в течение короткого периода времени.
• Контактная динамика – Движение систем многих тел
• Контактное сопротивление - электрическое сопротивление, связанное с контактирующими интерфейсами (ECR).
• Дисперсионная адгезия - Адгезия между материалами за счет межмолекулярных взаимодействий.
• Электростатический генератор - устройство, генерирующее электрический заряд на электроде высокого напряжения.
• Энергетически модифицированный цемент - класс цементов, механически обработанных для изменения реакционной способности.
• Механика фрикционного контакта - Исследование деформирования тел при наличии эффектов трения.
• Фрикционный привод – механическая передача энергии за счет трения между компонентами.
• Истирание - форма износа, вызванная сцеплением между поверхностями скольжения.
• Гониометр – прибор для измерения угла
• Негладкая механика - подход к моделированию в механике.
• Полиэтиленовая пленка – тонкая пластиковая пленка, используемая для запечатывания пищевых продуктов.
• Прокатка (металлообработка) – процесс обработки металлов давлением.
• Удар (механика) – внезапное переходное ускорение.
• Задача Синьорини - Задача эластостатики в линейной упругости
• Поверхностное натяжение - тенденция поверхности жидкости сжиматься с целью уменьшения площади поверхности.
• Трибология - наука и техника взаимодействующих поверхностей в относительном движении.
• Односторонний контакт - механическое ограничение, предотвращающее проникновение между двумя телами.
• Смачивание – способность жидкости сохранять контакт с твердой поверхностью.

Ссылки

См. Также: Контактная механика для мягкого полуэллиптического кончика пальца.

Внешние ссылки

• [1] : Дополнительную информацию о контактных напряжениях и эволюции уравнений напряжения в подшипниках можно найти в этой публикации Эрвина Зарецкого, руководителя отдела подшипников, зубчатых передач и трансмиссий НАСА, Исследовательского центра Гленна НАСА.
• [2] : Программа MATLAB для решения задачи механики линейного упругого контакта под названием; «Решение LCP задачи механики линейного упругого контакта» предоставляется при обмене файлами в MATLAB Central.
• [3] : Калькулятор контактной механики.
• [4] : подробные расчеты и формулы теории JKR для двух сфер.
• [5] : Программа Matlab для контактного анализа Герца (включает линейные, точечные и эллиптические случаи).
• [6] : модели адгезии JKR, MD и DMT (программы Matlab).