Плоское напряжение

Рисунок 7.1. Плоское напряженное состояние в сплошной среде.

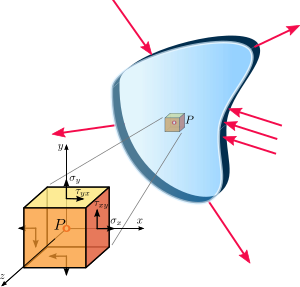
В механике сплошной среды говорят, что материал находится под плоским напряжением , если вектор напряжения в определенной плоскости равен нулю. Когда такая ситуация возникает по всему элементу конструкции, как это часто бывает с тонкими пластинами, анализ напряжений значительно упрощается, поскольку напряженное состояние может быть представлено тензором размерности 2 (представленным в виде матрицы 2×2, а не в виде матрицы 2×2). чем 3×3). Родственное понятие — плоская деформация — часто применимо к очень толстым элементам.

Плоское напряжение обычно возникает в тонких плоских пластинах, на которые действуют только параллельные им силы нагрузки. В некоторых ситуациях для целей анализа напряжений можно также предположить, что слегка изогнутая тонкая пластина имеет плоское напряжение. Так обстоит дело, например, с тонкостенным цилиндром, наполненным жидкостью под давлением. В таких случаях составляющие напряжения, перпендикулярные пластине, пренебрежимо малы по сравнению с параллельными ей.

Однако в других ситуациях нельзя пренебрегать напряжением изгиба тонкой пластины. Анализ по-прежнему можно упростить, используя двумерную область, но тензор плоских напряжений в каждой точке необходимо дополнить членами изгиба.

Математическое определение

Математически напряжение в некоторой точке материала является плоским напряжением, если одно из трех главных напряжений ( собственных значений тензора напряжений Коши ) равно нулю. То есть существует декартова система координат , в которой тензор напряжений имеет вид

$\sigma ={\begin{bmatrix}\sigma _{11}&0&0\\0&\sigma _{22}&0\\0&0&0\end{bmatrix}}\equiv {\begin{bmatrix}\sigma _{x}&0&0\\0&\sigma _{y}&0\\0&0&0\end{bmatrix}}$

Например, рассмотрим прямоугольный блок материала размером 10, 40 и 5 см по длине. $x$, $y$, и $z$, который растягивается в $x$ направлении и сжат в $y$ направлении парами противоположных сил величиной 10 Н и 20 Н соответственно, равномерно распределенных по соответствующим граням. Тензор напряжений внутри блока будет

$\sigma ={\begin{bmatrix}500\mathrm {Pa} &0&0\\0&-4000\mathrm {Pa} &0\\0&0&0\end{bmatrix}}$

В более общем смысле, если первые две оси координат выбрать произвольно, но перпендикулярно направлению нулевого напряжения, тензор напряжений будет иметь вид

$\sigma ={\begin{bmatrix}\sigma _{11}&\sigma _{12}&0\\\sigma _{21}&\sigma _{22}&0\\0&0&0\end{bmatrix}}\equiv {\begin{bmatrix}\sigma _{x}&\tau _{xy}&0\\\tau _{yx}&\sigma _{y}&0\\0&0&0\end{bmatrix}}$

и поэтому может быть представлен матрицей 2 × 2,

$\sigma _{ij}={\begin{bmatrix}\sigma _{11}&\sigma _{12}\\\sigma _{21}&\sigma _{22}\end{bmatrix}}\equiv {\begin{bmatrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\end{bmatrix}}$

Определяющие уравнения

Основная статья: Закон Гука § Плоское напряжение

Плоское напряжение на изогнутых поверхностях

В некоторых случаях модель плоских напряжений можно использовать при анализе слегка искривленных поверхностей. Например,Рассмотрим тонкостенный цилиндр, на который действует осевая сжимающая нагрузка, равномерно распределенная по его ободу, и заполненный жидкостью под давлением. Внутреннее давление создаст реактивное окружное напряжение на стенке , нормальное растягивающее напряжение, направленное перпендикулярно оси цилиндра и по касательной к его поверхности. Цилиндр можно концептуально развернуть и проанализировать как плоскую тонкую прямоугольную пластину, подвергающуюся растягивающей нагрузке в одном направлении и сжимающей нагрузке в другом направлении, причем обе нагрузки параллельны пластине.

Плоская деформация (матрица деформаций)

Рис. 7.2. Плоскодеформированное состояние в сплошной среде.

Основная статья: Теория бесконечно малых деформаций

Если одно измерение очень велико по сравнению с другими, основная деформация в направлении самого длинного измерения ограничена и может считаться постоянной, что означает, что деформация вдоль него будет практически нулевой, что приводит к состоянию плоской деформации (рис. 7.2). ). В этом случае, хотя все главные напряжения отличны от нуля, главное напряжение в направлении самого длинного измерения можно не учитывать при расчетах. Таким образом, можно провести двумерный анализ напряжений, например, анализ плотины в поперечном сечении, нагруженном водохранилищем.

Соответствующий тензор деформации:

$\varepsilon _{ij}={\begin{bmatrix}\varepsilon _{11}&\varepsilon _{12}&0\\\varepsilon _{21}&\varepsilon _{22}&0\\0&0&0\end{bmatrix}}\,\!$

и соответствующий тензор напряжений:

$\sigma _{ij}={\begin{bmatrix}\sigma _{11}&\sigma _{12}&0\\\sigma _{21}&\sigma _{22}&0\\0&0&\sigma _{33}\end{bmatrix}}\,\!$

в котором ненулевое $\sigma _{33}\,\!$ член возникает из-за эффекта Пуассона . Однако этот термин можно временно удалить из анализа напряжений, оставив только термины в плоскости, что эффективно сводит анализ к двум измерениям.

Трансформация напряжений при плоском напряжении и плоской деформации.

Рассмотрим точку $P\,\!$ в сплошной среде в состоянии плоского напряжения или плоской деформации с компонентами напряжения $(\sigma _{x},\sigma _{y},\tau _{xy})\,\!$ а все остальные компоненты напряжений равны нулю (рисунок 8.1). Из статического равновесия бесконечно малого материального элемента при $P\,\!$ (рис. 8.2), нормальное напряжение $\sigma _{\mathrm {n} }\,\!$ и напряжение сдвига $\tau _{\mathrm {n} }\,\!$ в любой плоскости, перпендикулярной $x\,\!$- $y\,\!$ самолет, проходящий через $P\,\!$ с единичным вектором $\mathbf {n} \,\!$ делая угол $\theta \,\!$ с горизонталью, т.е. $\cos \theta \,\!$ это направляющий косинус $x\,\!$ направление определяется:

$\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta \,\!$

$\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta \,\!$

Эти уравнения показывают, что в условиях плоского напряжения или плоской деформации можно определить компоненты напряжения в точке во всех направлениях, т. е. как функцию $\theta \,\!$, если известны компоненты напряжений $(\sigma _{x},\sigma _{y},\tau _{xy})\,\!$ в любых двух перпендикулярных направлениях в этой точке. Важно помнить, что мы рассматриваем единицу площади бесконечно малого элемента в направлении, параллельном $y\,\!$- $z\,\!$ самолет.

Рисунок 8.1 – Трансформация напряжений в точке сплошной среды в условиях плоского напряжения.

Рисунок 8.2 – Компоненты напряжений на плоскости, проходящей через точку сплошной среды, в условиях плоского напряжения.

Главные направления (рис. 8.3), т. е. ориентацию плоскостей, в которых компоненты касательного напряжения равны нулю, можно получить, составив предыдущее уравнение для касательного напряжения. $\tau _{\mathrm {n} }\,\!$ равен нулю. Таким образом мы имеем:

$\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta =0\,\!$

и мы получаем

$\tan 2\theta _{\mathrm {p} }={\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}\,\!$

Это уравнение определяет два значения $\theta _{\mathrm {p} }\,\!$ которые $90^{\circ }\,\!$ друг от друга (рис. 8.3). Тот же результат можно получить, найдя угол $\theta \,\!$ что делает нормальный стресс $\sigma _{\mathrm {n} }\,\!$ максимум, т.е. ${\frac {d\sigma _{\mathrm {n} }}{d\theta }}=0\,\!$

Главные напряжения $\sigma _{1}\,\!$ и $\sigma _{2}\,\!$, или минимальное и максимальное нормальные напряжения $\sigma _{\mathrm {max} }\,\!$ и $\sigma _{\mathrm {min} }\,\!$соответственно, можно получить заменой обоих значений $\theta _{\mathrm {p} }\,\!$ в предыдущее уравнение для $\sigma _{\mathrm {n} }\,\!$. Этого можно добиться, переставив уравнения для $\sigma _{\mathrm {n} }\,\!$ и $\tau _{\mathrm {n} }\,\!$, сначала транспонируя первый член первого уравнения и возводя в квадрат обе части каждого из уравнений, а затем складывая их. Таким образом, мы имеем

$\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\,\!$

$(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}=R^{2}\,\!$

где

$R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\,\!$

которое представляет собой уравнение окружности радиуса $R\,\!$ центрирован в точке с координатами $[\sigma _{\mathrm {avg} },0]\,\!$, называемый кругом Мора . Но зная, что для главных напряжений напряжение сдвига $\tau _{\mathrm {n} }=0\,\!$, то из этого уравнения получаем:

$\sigma _{1}=\sigma _{\mathrm {max} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})+{\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\,\!$

$\sigma _{2}=\sigma _{\mathrm {min} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})-{\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\,\!$

Рисунок 8.3 – Трансформация напряжений в двух измерениях с указанием плоскостей действия главных напряжений, а также максимальных и минимальных касательных напряжений.

Когда $\tau _{xy}=0\,\!$ бесконечно малый элемент ориентирован в направлении главных плоскостей, поэтому напряжения, действующие на прямоугольный элемент, являются главными напряжениями: $\sigma _{x}=\sigma _{1}\,\!$ и $\sigma _{y}=\sigma _{2}\,\!$. Тогда обычный стресс $\sigma _{\mathrm {n} }\,\!$ и напряжение сдвига $\tau _{\mathrm {n} }\,\!$ как функцию главных напряжений можно определить, сделав $\tau _{xy}=0\,\!$. Таким образом, мы имеем

$\sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{1}+\sigma _{2})+{\frac {1}{2}}(\sigma _{1}-\sigma _{2})\cos 2\theta \,\!$

$\tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{1}-\sigma _{2})\sin 2\theta \,\!$

Тогда максимальное напряжение сдвига $\tau _{\mathrm {max} }\,\!$ происходит, когда $\sin 2\theta =1\,\!$, то есть $\theta =45^{\circ }\,\!$ (рис. 8.3):

$\tau _{\mathrm {max} }={\frac {1}{2}}(\sigma _{1}-\sigma _{2})\,\!$

Тогда минимальное напряжение сдвига $\tau _{\mathrm {min} }\,\!$ происходит, когда $\sin 2\theta =-1\,\!$, то есть $\theta =135^{\circ }\,\!$ (рис. 8.3):

$\tau _{\mathrm {min} }=-{\frac {1}{2}}(\sigma _{1}-\sigma _{2})\,\!$

См. также

• Плоская деформация