вязкоупругость

В материаловедении и механике сплошных сред вязкоупругость — это свойство материалов проявляют как вязкие , так и упругие , которые при деформации характеристики . Вязкие материалы, такие как вода, сопротивляются как сдвиговому течению , так и линейно деформируются со временем при напряжения приложении . Эластичные материалы деформируются при растяжении и сразу же возвращаются в исходное состояние после снятия напряжения.

Вязкоэластичные материалы обладают элементами обоих этих свойств и, как таковые, демонстрируют зависящую от времени деформацию. В то время как эластичность обычно является результатом растяжения связей вдоль кристаллографических плоскостей в упорядоченном твердом теле, вязкость является результатом диффузии атомов или молекул внутри аморфного материала. ^[1]

Фон

В девятнадцатом веке такие физики, как Джеймс Клерк Максвелл , Людвиг Больцман и лорд Кельвин , исследовали и экспериментировали с ползучестью и восстановлением стекла , металлов и резин . Дальнейшие исследования вязкоупругости проводились в конце двадцатого века, когда были разработаны синтетические полимеры , которые стали использовать в различных областях. ^[2] Расчеты вязкоупругости сильно зависят от вязкости переменной η . Обратная величина η также известна как текучесть , φ . Значение любого из них может быть получено как функция температуры или как заданное значение (например, для приборной панели ). ^[1]

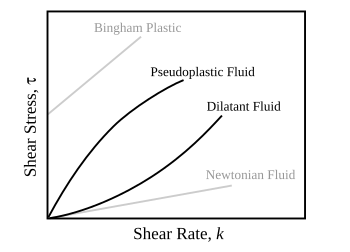
В зависимости от изменения скорости деформации в зависимости от напряжения внутри материала вязкость можно разделить на линейную, нелинейную или пластическую. Когда материал демонстрирует линейный отклик, его классифицируют как ньютоновский материал . В этом случае напряжение линейно пропорционально скорости деформации. Если материал демонстрирует нелинейную реакцию на скорость деформации, его классифицируют как неньютоновскую жидкость . Существует также интересный случай, когда вязкость уменьшается, поскольку скорость сдвига/деформации остается постоянной. Материал, который демонстрирует такое поведение, известен как тиксотропный . Кроме того, когда напряжение не зависит от скорости деформации, материал демонстрирует пластическую деформацию. ^[1] Многие вязкоупругие материалы демонстрируют поведение, подобное резине , что объясняется термодинамической теорией эластичности полимеров.

Некоторыми примерами вязкоупругих материалов являются аморфные полимеры, полукристаллические полимеры, биополимеры, металлы при очень высоких температурах и битумные материалы. Растрескивание происходит, когда напряжение прикладывается быстро и выходит за пределы упругости. Связки и сухожилия вязкоупругие, поэтому степень потенциального их повреждения зависит как от скорости изменения их длины, так и от приложенной силы. ^{[ нужна ссылка ]}

Вязкоэластичный материал обладает следующими свойствами:

гистерезис виден на кривой напряжение-деформация
происходит релаксация напряжений : ступенчатая постоянная деформация вызывает уменьшение напряжения
происходит ползучесть : шаг постоянного напряжения вызывает увеличение деформации
его жесткость зависит от скорости деформации ${\dot {\varepsilon }}$ или уровень стресса ${\dot {\sigma }}$

Упругое и вязкоупругое поведение

Кривые растяжения для чисто упругого материала (а) и вязкоупругого материала (б). Красная область представляет собой петлю гистерезиса и показывает количество энергии, теряемой (в виде тепла) в цикле загрузки и разгрузки. Это равно ${\textstyle \oint \sigma \,d\varepsilon }$ , где $\sigma$ это стресс и $\varepsilon$ это напряжение. ^[1]

В отличие от чисто упругих веществ, вязкоупругое вещество имеет упругую составляющую и вязкую составляющую. Вязкость вязкоупругого вещества придает веществу зависимость скорости деформации от времени. Чисто эластичные материалы не рассеивают энергию (тепло) при приложении нагрузки, а затем ее снятии. Однако вязкоупругое вещество рассеивает энергию при приложении нагрузки, а затем снимается. гистерезис На кривой растяжения наблюдается , при этом площадь петли равна энергии, теряемой за цикл нагружения. Поскольку вязкость — это сопротивление термически активированной пластической деформации, вязкий материал будет терять энергию в ходе цикла нагрузки. Пластическая деформация приводит к потере энергии, что нехарактерно для реакции чисто упругого материала на цикл нагрузки. ^[1]

В частности, вязкоупругость представляет собой молекулярную перегруппировку. , прилагается напряжение Когда к вязкоупругому материалу, такому как полимер , части длинной полимерной цепи меняют положение. Это движение или перестановка называется ползучестью . Полимеры остаются твердым материалом, даже когда эти части их цепей перестраиваются, чтобы выдержать напряжение, и когда это происходит, в материале создается обратное напряжение. Когда обратное напряжение имеет ту же величину, что и приложенное напряжение, материал больше не ползет. Когда исходное напряжение снимается, накопленные обратные напряжения заставят полимер вернуться в исходную форму. Материал расползается, что дает приставку вязко-, а материал полностью восстанавливается, что дает суффикс -эластичность. ^[2]

Линейная вязкоупругость и нелинейная вязкоупругость

Линейная вязкоупругость - это когда функция разделима как по реакции ползучести, так и по нагрузке. Все линейные вязкоупругие модели могут быть представлены уравнением Вольтерра, связывающим напряжение и деформацию : $\varepsilon (t)={\frac {\sigma (t)}{E_{\text{inst,creep}}}}+\int _{0}^{t}K(t-t'){\dot {\sigma }}(t')dt'$ или $\sigma (t)=E_{\text{inst,relax}}\varepsilon (t)+\int _{0}^{t}F(t-t'){\dot {\varepsilon }}(t')dt'$ где

$пришло$ время
$\sigma (t)$ это стресс
$\varepsilon (t)$ напряжение
$E_{\text{inst,creep}}$ и $E_{\text{inst,relax}}$ — мгновенные модули упругости для ползучести и релаксации.
$K (t)$ — ползучести функция
$F (t)$ — функция релаксации

Линейная вязкоупругость обычно применима только при небольших деформациях .

Нелинейная вязкоупругость – это когда функция неразделима. Обычно это происходит при больших деформациях или при изменении свойств материала при деформациях. Нелинейная вязкоупругость также объясняет наблюдаемые явления, такие как нормальные напряжения, утончение при сдвиге и утолщение при растяжении в вязкоупругих жидкостях. ^[3]

Неэластичный материал представляет собой частный случай вязкоупругого материала: неэластичный материал полностью восстанавливается до исходного состояния после снятия нагрузки.

При различении упругого, вязкого и вязкоупругого поведения полезно ссылаться на временную шкалу измерения относительно времени релаксации наблюдаемого материала, известного как число Деборы (De), где: ^[3] $De=\lambda /t$ где

$\lambda$ время релаксации материала
$t$ пора

Динамический модуль

Вязкоупругость изучают с помощью динамического механического анализа , применяя небольшое колебательное напряжение и измеряя возникающую в результате деформацию.

В чисто упругих материалах напряжение и деформация совпадают по фазе, поэтому реакция одного на другое происходит мгновенно.
В чисто вязких материалах деформация отстает от напряжения на 90 градусов.
Вязкоэластичные материалы демонстрируют поведение где-то посередине между этими двумя типами материалов, демонстрируя некоторое отставание в деформации.

Комплексный динамический модуль G можно использовать для представления отношений между осциллирующим напряжением и деформацией: $G=G'+iG''$ где $i^{2}=-1$ ; $G'$ модуль упругости и $G''$ модуль потерь : $G'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \delta$ $G''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \delta$ где $\sigma _{0}$ и $\varepsilon _{0}$ - амплитуды напряжения и деформации соответственно, и $\delta$ фазовый сдвиг между ними.

Конститутивные модели линейной вязкоупругости

Вязкоэластичные материалы, такие как аморфные полимеры, полукристаллические полимеры, биополимеры и даже живые ткани и клетки, ^[4] могут быть смоделированы для определения их взаимодействия напряжения и деформации или силы и смещения, а также их временных зависимостей. Эти модели, в том числе модель Максвелла , модель Кельвина-Фойгта , стандартная линейная твердотельная модель и модель Бюргерса , используются для прогнозирования реакции материала при различных условиях нагрузки.

Вязкоупругое поведение имеет упругие и вязкие компоненты, смоделированные как линейные комбинации пружин и демпферов соответственно. Каждая модель отличается расположением этих элементов, и все эти вязкоупругие модели можно эквивалентно смоделировать как электрические цепи.

В эквивалентной электрической цепи напряжение представлено током, а скорость деформации — напряжением. Модуль упругости пружины аналогичен обратной величине индуктивности цепи (она сохраняет энергию), а вязкости приборной панели - сопротивлению цепи (она рассеивает энергию).

Упругие компоненты, как упоминалось ранее, можно смоделировать как пружины с константой упругости E по формуле: $\sigma =E\varepsilon$ где σ — напряжение, E — модуль упругости материала, а ε — деформация, возникающая при данном напряжении, аналогично закону Гука .

Вязкие компоненты можно смоделировать как точечные диаграммы, так что зависимость скорости напряжения от деформации можно представить как: $\sigma =\eta {\frac {d\varepsilon }{dt}}$ где σ — напряжение, η — вязкость материала, а dε/dt — производная деформации по времени.

Взаимосвязь между напряжением и деформацией можно упростить для конкретных скоростей напряжения или деформации. Для высоких напряжений или скоростей деформации/коротких периодов времени преобладают производные по времени компоненты зависимости напряжение-деформация. В этих условиях его можно представить как жесткий стержень, способный выдерживать большие нагрузки, не деформируясь. Следовательно, приборную панель можно рассматривать как «короткое замыкание». ^[5]^[6]

И наоборот, для состояний с низким напряжением/более длительных периодов времени компоненты производной по времени незначительны, и приборную панель можно эффективно удалить из системы – «разомкнутую» цепь. ^[6] В результате только пружина, подключенная параллельно приборной панели, будет способствовать общей нагрузке в системе. ^[5]

Модель Максвелла

Модель Максвелла можно представить чисто вязкостным демпфером и чисто упругой пружиной, соединенными последовательно, как показано на схеме. Модель может быть представлена следующим уравнением: $\sigma +{\frac {\eta }{E}}{\dot {\sigma }}=\eta {\dot {\varepsilon }}$

Согласно этой модели, если материал подвергается постоянной нагрузке, напряжения постепенно ослабляются . Когда материал подвергается постоянному напряжению, деформация состоит из двух компонентов. Во-первых, мгновенно возникает упругая составляющая, соответствующая пружине, и сразу же расслабляется после снятия напряжения. Вторая — вязкая составляющая, которая растет со временем по мере приложения напряжения. Модель Максвелла предсказывает, что напряжение спадает экспоненциально со временем, что верно для большинства полимеров. Одним из ограничений этой модели является то, что она не позволяет точно предсказать ползучесть. Модель Максвелла для условий ползучести или постоянного напряжения постулирует, что деформация будет увеличиваться линейно со временем. Однако для большинства полимеров скорость деформации со временем снижается. ^[2]

Эту модель можно применять к мягким твердым телам: термопластичным полимерам вблизи температуры их плавления, свежему бетону (без учета его старения) и многочисленным металлам при температуре, близкой к температуре их плавления.

Однако представленное здесь уравнение не имеет последовательного вывода из более микроскопической модели и не является независимым от наблюдателя. Модель Максвелла с верхней конвекцией представляет собой ее обоснованную формулировку в терминах тензора напряжений Коши и представляет собой простейшую тензорную конститутивную модель вязкоупругости (см., например, ^[7] или ^[6] ).

Модель Кельвина – Фойгта

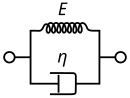
Модель Кельвина-Фойгта, также известная как модель Фойгта, состоит из ньютоновского демпфера и упругой пружины Гука, соединенных параллельно, как показано на рисунке. Он используется для объяснения ползучести полимеров.

Определяющее соотношение выражается в виде линейного дифференциального уравнения первого порядка: $\sigma =E\varepsilon +\eta {\dot {\varepsilon }}$

Эта модель представляет собой твердое тело, испытывающее обратимую вязкоупругую деформацию. При приложении постоянного напряжения материал деформируется с уменьшающейся скоростью, асимптотически приближаясь к установившейся деформации. Когда напряжение снимается, материал постепенно расслабляется до недеформированного состояния. При постоянном напряжении (ползучести) модель вполне реалистична, поскольку предсказывает, что деформация будет стремиться к σ/E по мере того, как время будет стремиться к бесконечности. Подобно модели Максвелла, модель Кельвина – Фойгта также имеет ограничения. Модель чрезвычайно хороша для моделирования ползучести материалов, но в отношении релаксации модель гораздо менее точна. ^[8]

Эту модель можно применять к органическим полимерам, резине и дереву, когда нагрузка не слишком велика.

Стандартная линейная твердотельная модель

Стандартная линейная твердотельная модель, также известная как модель Зенера, состоит из двух пружин и приборной панели. Это простейшая модель, которая правильно описывает как ползучесть, так и поведение релаксации напряжений вязкоупругого материала. Для этой модели определяющими отношениями являются:

Представление Максвелла	Представление Кельвина

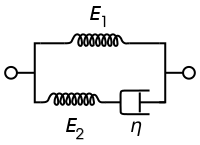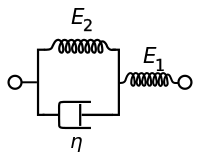$\sigma +{\frac {\eta }{E_{2}}}{\dot {\sigma }}=E_{1}\varepsilon +{\frac {\eta (E_{1}+E_{2})}{E_{2}}}{\dot {\varepsilon }}$	$\sigma +{\frac {\eta }{E_{1}+E_{2}}}{\dot {\sigma }}={\frac {E_{1}E_{2}}{E_{1}+E_{2}}}\varepsilon +{\frac {E_{1}\eta }{E_{1}+E_{2}}}{\dot {\varepsilon }}$

Под постоянным напряжением моделируемый материал мгновенно деформируется до некоторой деформации, которая представляет собой мгновенную упругую часть деформации. После этого он продолжит деформироваться и асимптотически приближается к установившейся деформации, которая представляет собой запаздывающую упругую часть деформации. Хотя стандартная линейная твердотельная модель более точна, чем модели Максвелла и Кельвина-Фойгта в прогнозировании реакции материала, математически она дает неточные результаты для деформации в конкретных условиях нагрузки.

Модель Джеффриса

Модель Джеффриса, как и модель Зинера, представляет собой трехэлементную модель. Он состоит из двух толкателей и пружины. ^[9]

Он был предложен в 1929 году Гарольдом Джеффрисом для изучения мантии Земли . ^[10]

Модель бургеров

Модель Бюргерса состоит либо из двух параллельно включенных компонентов Максвелла, либо из компонента Кельвина-Фойгта, пружины и приборной панели, соединенных последовательно. Для этой модели определяющими отношениями являются:

Представление Максвелла	Представление Кельвина

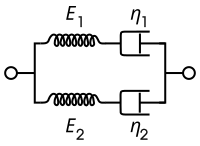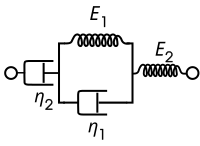$\sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\left(\eta _{1}+\eta _{2}\right){\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}\left(E_{1}+E_{2}\right)}{E_{1}E_{2}}}{\ddot {\varepsilon }}$	$\sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\eta _{2}{\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}}{E_{1}}}{\ddot {\varepsilon }}$

Эта модель включает вязкое течение в стандартную линейную твердотельную модель, что дает линейно возрастающую асимптоту деформации при фиксированных условиях нагрузки.

Обобщенная модель Максвелла

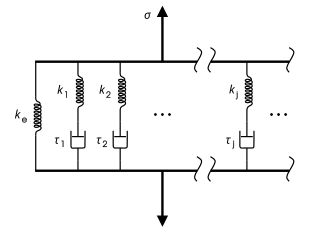
Обобщенная модель Максвелла, также известная как модель Вихерта, представляет собой наиболее общую форму линейной модели вязкоупругости. При этом учитывается, что релаксация происходит не единовременно, а в разное время. Из-за того, что молекулярные сегменты разной длины, причем более короткие вносят меньший вклад, чем более длинные, существует различное временное распределение. Модель Вихерта показывает это, имея столько элементов Максвелла, сколько необходимо для точного представления распределения. На рисунке справа показана обобщенная модель Вихерта. ^[11]Область применения: металлы и сплавы при температурах ниже четверти их абсолютной температуры плавления (выраженной в К).

Определяющие модели нелинейной вязкоупругости

Нелинейные вязкоупругие определяющие уравнения необходимы для количественного объяснения таких явлений в жидкостях, как различия в нормальных напряжениях, утончение при сдвиге и утолщение при растяжении. ^[3] Обязательно история, переживаемая материалом, необходима для учета зависящего от времени поведения и обычно включается в модели как ядро истории K . ^[12]

Жидкость второго порядка

Жидкость второго порядка обычно считается простейшей нелинейной вязкоупругой моделью и обычно встречается в узкой области поведения материалов, возникающей при высоких амплитудах деформации и числе Деборы, между ньютоновскими жидкостями и другими более сложными нелинейными вязкоупругими жидкостями. ^[3] Определяющее уравнение жидкости второго порядка имеет вид:

$\mathbf {T} =-p\mathbf {I} +2\eta _{0}\mathbf {D} -\psi _{1}\mathbf {D} ^{\triangledown }+4\psi _{2}\mathbf {D} \bullet \mathbf {D}$

где:

$\mathbf {I}$ это тождественный тензор
$\mathbf {D}$ – тензор деформации
$\eta _{0},\psi _{1},\psi _{2}$ обозначают вязкость, а первый и второй коэффициенты нормальных напряжений соответственно
$\mathbf {D} ^{\triangledown }$ обозначает конвекционную сверху производную тензора деформации, где $\mathbf {D} ^{\triangledown }\equiv {\dot {\mathbf {D} }}-(\bigtriangledown \mathbf {v} )^{\mathbf {T} }\bullet \mathbf {D} -\mathbf {D} \bullet \bigtriangledown \mathbf {v}$ и ${\dot {\mathbf {D} }}\equiv {\frac {\partial }{\partial t}}\mathbf {D} +\mathbf {v} \bullet \bigtriangledown \mathbf {D}$ – материальная производная по времени тензора деформации. ^[3]

Модель Максвелла с верхней конвекцией

Модель Максвелла с верхней конвекцией включает нелинейное поведение во времени в вязкоупругую модель Максвелла, определяемую следующим образом: ^[3]

$\mathbf {\tau } +\lambda \mathbf {\tau } ^{\triangledown }=2\eta _{0}\mathbf {D}$ где $\mathbf {\tau }$ обозначает тензор напряжений.

Модель Олдройд-Б

Модель Олдройда-Б является расширением модели Максвелла с верхней конвекцией и интерпретируется как растворитель, наполненный упругими шариками и пружинными гантелями.Модель названа в честь своего создателя Джеймса Г. Олдройда . ^[13]^[14]^[15]

Модель можно записать как: $\mathbf {T} +\lambda _{1}{\stackrel {\nabla }{\mathbf {T} }}=2\eta _{0}(\mathbf {D} +\lambda _{2}{\stackrel {\nabla }{\mathbf {D} }})$ где:

$\mathbf {T}$ – напряжений тензор ;
$\lambda _{1}$ – время релаксации;
$\lambda _{2}$ время замедления = ${\frac {\eta _{s}}{\eta _{0}}}\lambda _{1}$ ;
${\stackrel {\nabla }{\mathbf {T} }}$ – верхняя производная по времени конвекции тензора напряжений: ${\stackrel {\nabla }{\mathbf {T} }}={\frac {\partial }{\partial t}}\mathbf {T} +\mathbf {v} \cdot \nabla \mathbf {T} -((\nabla \mathbf {v} )^{T}\cdot \mathbf {T} +\mathbf {T} \cdot (\nabla \mathbf {v} ));$
$\mathbf {v}$ – скорость жидкости;
$\eta _{0}$ — общая вязкость, состоящая из растворителя и полимерных компонентов, $\eta _{0}=\eta _{s}+\eta _{p}$ ;
$\mathbf {D}$ – тензор скорости деформации или тензор скорости деформации, $\mathbf {D} ={\frac {1}{2}}\left[{\boldsymbol {\nabla }}\mathbf {v} +({\boldsymbol {\nabla }}\mathbf {v} )^{T}\right]$ .

Хотя модель дает хорошие аппроксимации вязкоупругих жидкостей в сдвиговом потоке, она имеет нефизическую особенность в потоке растяжения, когда гантели бесконечно растягиваются. Однако это характерно для идеализированного потока; в случае геометрии с поперечными пазами поток при растяжении не является идеальным, поэтому напряжение, хотя и сингулярное, остается интегрируемым, хотя напряжение бесконечно в соответственно бесконечно малой области. ^[15]

Если вязкость растворителя равна нулю, модель Олдройда-Б становится верхней конвекционной моделью Максвелла .

Модель Вагнера

Модель Вагнера можно рассматривать как упрощенную практическую форму модели Бернштейна-Кирсли-Запаса. Модель разработал немецкий реолог Манфред Вагнер .

Для изотермических условий модель можно записать как: $\mathbf {\sigma } (t)=-p\mathbf {I} +\int _{-\infty }^{t}M(t-t')h(I_{1},I_{2})\mathbf {B} (t')\,dt'$

где:

$\mathbf {\sigma } (t)$ – тензор напряжений Коши как функция времени t ,
р - давление
$\mathbf {I}$ тензор единицы
M — функция памяти, обычно выражаемая как сумма экспоненциальных членов для каждого режима релаксации : $M(x)=\sum _{k=1}^{m}{\frac {g_{i}}{\theta _{i}}}\exp \left({\frac {-x}{\theta _{i}}}\right),$ где для каждого режима релаксации $g_{i}$ модуль релаксации и $\theta _{i}$ – время релаксации;
$h(I_{1},I_{2})$ — функция демпфирования деформации , которая зависит от первого и второго инвариантов тензора Фингера. $\mathbf {B}$ .

Функция демпфирования деформации обычно записывается как: $h(I_{1},I_{2})=m^{*}\exp(-n_{1}{\sqrt {I_{1}-3}})+(1-m^{*})\exp(-n_{2}{\sqrt {I_{2}-3}})$ Если значение функции деформационного упрочнения равно единице, то деформация мала; если оно приближается к нулю, то деформации большие. ^[16]^[17]

Серия Прони

При одномерном испытании на релаксацию материал подвергается внезапной деформации, которая остается постоянной на протяжении всего испытания, и напряжение измеряется с течением времени. Начальное напряжение возникает из-за упругой реакции материала. Затем напряжение со временем ослабевает из-за вязких эффектов в материале. Обычно применяется растяжение, сжатие, объемное сжатие или сдвиг. Полученные в результате данные зависимости напряжения от времени можно аппроксимировать рядом уравнений, называемых моделями. Меняются лишь обозначения в зависимости от вида приложенной деформации: обозначается растягивающе-сжимающая релаксация $E$ , сдвиг обозначается $G$ , объем обозначается $K$ . Ряд Прони для сдвиговой релаксации:

$G(t)=G_{\infty }+\sum _{i=1}^{N}G_{i}\exp(-t/\tau _{i})$

где $G_{\infty }$ - долговременный модуль упругости после полного расслабления материала, $\tau _{i}$ – времена релаксации (не путать с $\tau _{i}$ на схеме); чем выше их значения, тем больше времени требуется, чтобы стресс расслабился. Данные подгоняются под уравнение с использованием алгоритма минимизации, который корректирует параметры ( $G_{\infty },G_{i},\tau _{i}$ ), чтобы минимизировать ошибку между прогнозируемыми значениями и значениями данных. ^[18]

Альтернативная форма получается с учетом того, что модуль упругости связан с долговременным модулем следующим соотношением:

$G(t=0)=G_{0}=G_{\infty }+\sum _{i=1}^{N}G_{i}$

Поэтому,

$G(t)=G_{0}-\sum _{i=1}^{N}G_{i}\left[1-e^{-t/\tau _{i}}\right]$

Эта форма удобна, когда модуль упругого сдвига $G_{0}$ получается из данных, независимых от данных релаксации, и/или для компьютерной реализации, когда желательно указать упругие свойства отдельно от вязких свойств, как в Simulia (2010). ^[19]

Эксперимент по ползучести обычно легче провести, чем эксперимент по релаксации, поэтому большинство данных доступны в виде зависимости податливости (ползучести) от времени. ^[20] К сожалению, не существует закрытой формы податливости (ползучести) через коэффициент Прони.ряд. Итак, имея данные о ползучести, нелегко получить коэффициенты ряда (релаксации) Прони, которые нужны, например, в . ^[19] Целесообразным способом получения этих коэффициентов является следующий. Во-первых, адаптируйте данные о ползучести к модели, которая имеет решения в замкнутой форме как по податливости, так и по релаксации; например модель Максвелла-Кельвина(уравнение 7.18-7.19) в Барберо (2007 г.) ^[21] или Стандартная твердотельная модель (уравнения 7.20–7.21) в Барберо (2007). ^[21] (раздел 7.1.3). Как только параметры модели ползучести станут известны, создайте псевдоданные релаксации с помощью модели сопряженной релаксации для тех же самых параметров.раз исходных данных. Наконец, согласуйте псевдоданные с рядом Прони.

Влияние температуры

Вторичные связи полимера постоянно разрываются и восстанавливаются из-за теплового движения. Приложение напряжения благоприятствует одним конформациям по сравнению с другими, поэтому молекулы полимера со временем постепенно «перетекают» в предпочтительные конформации. ^[22] Поскольку тепловое движение является одним из факторов, способствующих деформации полимеров, вязкоупругие свойства изменяются с увеличением или понижением температуры. В большинстве случаев модуль ползучести, определяемый как отношение приложенного напряжения к зависящей от времени деформации, уменьшается с увеличением температуры. Вообще говоря, повышение температуры коррелирует с логарифмическим уменьшением времени, необходимого для придания одинаковой деформации при постоянном напряжении. Другими словами, для растяжения вязкоупругого материала на равное расстояние при более высокой температуре требуется меньше работы, чем при более низкой температуре.

Более детальное влияние температуры на вязкоупругое поведение полимера можно отобразить, как показано.

В типичные полимеры входят в основном пять областей (некоторые обозначают четыре, которые объединяют IV и V). ^[23]

Область I: В этой области присутствует стеклообразное состояние полимера. Температура в этой области для данного полимера слишком низка, чтобы обеспечить молекулярное движение. Следовательно, движение молекул в этой области заморожено. Механические свойства в этой области твердые и хрупкие. ^[24]
Область II: В этой области полимер достигает температуры стеклования. За пределами Tg тепловой энергии, обеспечиваемой окружающей средой, достаточно, чтобы разморозить движение молекул. Молекулы могут совершать локальное движение в этой области, что приводит к резкому падению жесткости по сравнению с областью I.
Регион III: регион каучукового плато. Материалы, находящиеся в этой области, обладают эластичностью на большие расстояния, обусловленной энтропией. Например, резиновая лента в исходном состоянии этой области разупорядочена. Растягивая резинку, вы также выравниваете конструкцию, делая ее более упорядоченной. Следовательно, при отпускании резиновой ленты она самопроизвольно будет искать состояние с более высокой энтропией и, следовательно, вернется в исходное состояние. Это то, что мы назвали восстановлением формы упругости, обусловленной энтропией.
Область IV: Поведение в области эластичного течения сильно зависит от времени. Полимерам в этом регионе придется использовать суперпозицию времени и температуры, чтобы получить более подробную информацию и осторожно решить, как использовать материалы. Например, если материал используется для кратковременного взаимодействия, он может представлять собой «твердый» материал. При использовании для длительного взаимодействия он будет действовать как «мягкий» материал. ^[25]
Область V: В этой области вязкий полимер легко течет. Еще одно существенное снижение жесткости.

Экстремально низкие температуры могут привести к тому, что вязкоупругие материалы перейдут в стеклообразную фазу и станут хрупкими . Например, воздействие чувствительные к давлению клеи сильного холода на ( сухой лед , замораживающий спрей и т. д.) приводит к потере клейкости, что приводит к отслоению клея.

Вязкоупругая ползучесть

а) Приложенное напряжение и б) вызванная деформация как функции времени в течение короткого периода времени для вязкоупругого материала.

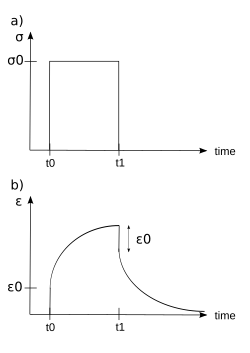
Под воздействием ступенчатого постоянного напряжения вязкоупругие материалы испытывают зависящее от времени увеличение деформации. Это явление известно как вязкоупругая ползучесть.

Во время $t_{0}$ , вязкоупругий материал нагружается постоянным напряжением, которое сохраняется в течение достаточно длительного периода времени. Материал реагирует на напряжение деформацией, которая увеличивается до тех пор, пока материал в конечном итоге не выйдет из строя, если это вязкоупругая жидкость. С другой стороны, если это вязкоупругое твердое тело, оно может разрушиться, а может и не разрушиться, в зависимости от приложенного напряжения и предельного сопротивления материала. При сохранении напряжения в течение более короткого периода времени материал испытывает первоначальную деформацию до момента, когда $t_{1}$ , после чего деформация сразу уменьшается (разрыв), затем постепенно уменьшается в разы $t>t_{1}$ до остаточной деформации.

Данные вязкоупругой ползучести можно представить путем построения графика модуля ползучести (постоянного приложенного напряжения, деленного на общую деформацию в определенный момент времени) как функции времени. ^[26] Ниже критического напряжения модуль вязкоупругой ползучести не зависит от приложенного напряжения. Семейство кривых, описывающих реакцию деформации в зависимости от времени на различные приложенные напряжения, может быть представлено одной кривой зависимости модуля вязкоупругой ползучести от времени, если приложенные напряжения ниже критического значения напряжения материала.

Вязкоупругая ползучесть важна при рассмотрении долгосрочного проектирования конструкций. Учитывая условия нагрузки и температуры, проектировщики могут выбирать материалы, которые наилучшим образом соответствуют сроку службы компонентов.

Измерение

Сдвиговая реометрия

В основе сдвиговых реометров лежит идея помещения измеряемого материала между двумя пластинами, одна или обе из которых движутся в направлении сдвига, вызывая напряжения и деформации в материале. Испытание может проводиться при постоянной скорости деформации, напряжении или в колебательном режиме (форма динамического механического анализа ). ^[27] Сдвиговые реометры обычно ограничены краевыми эффектами, когда материал может вытекать между двумя пластинами и скользить на границе раздела материал/пластина.

Растяжительная реометрия

Реометры растяжения, также известные как экстензиометры, измеряют вязкоупругие свойства путем вытягивания вязкоупругой жидкости, обычно одноосно. ^[28] Поскольку при этом обычно используются капиллярные силы и ограничивается узкая геометрия жидкости, этот метод часто ограничивается жидкостями с относительно низкой вязкостью, такими как разбавленные растворы полимеров или некоторые расплавленные полимеры. ^[28] Экстенсионные реометры также ограничены краевыми эффектами на концах экстензиометра и разницей давлений внутри и снаружи капилляра. ^[3]

Несмотря на очевидные ограничения, упомянутые выше, реометрию растяжения можно также выполнять на жидкостях с высокой вязкостью. Хотя для этого требуется использование различных инструментов, эти методы и устройства позволяют изучать вязкоупругие свойства материалов, таких как расплавы полимеров, при растяжении. Тремя наиболее распространенными инструментами для экстенсионной реометрии, разработанными за последние 50 лет, являются реометр мейснеровского типа, реометр с растяжением нити (FiSER) и реометр для растяжения Сентманата (SER).

Реометр типа Мейснера, разработанный Мейсснером и Хостеттлером в 1996 году, использует два набора роликов, вращающихся в противоположных направлениях, для одноосного растяжения образца. ^[29] Этот метод использует постоянную длину образца на протяжении всего эксперимента и поддерживает образец между роликами с помощью воздушной подушки, чтобы исключить эффект провисания образца. У него есть несколько проблем: во-первых, жидкость может проскальзывать на ремнях, что приводит к более низкой скорости деформации, чем можно было бы ожидать. Кроме того, это оборудование сложно в эксплуатации, а его приобретение и обслуживание обходятся дорого.

Реометр FiSER просто содержит жидкость между двумя пластинами. Во время эксперимента верхнюю пластину удерживают неподвижно, а к нижней прикладывают силу, отодвигая ее от верхней. ^[30] Скорость деформации измеряется по скорости изменения радиуса образца в его середине. Он рассчитывается по следующему уравнению: ${\dot {\epsilon }}=-{\frac {2}{R}}{dR \over dt}$ где $R$ - значение среднего радиуса и ${\dot {\epsilon }}$ это скорость деформации. Вязкость образца затем рассчитывается по следующему уравнению: $\eta ={\frac {F}{\pi R^{2}{\dot {\epsilon }}}}$ где $\eta$ вязкость образца, $F$ — сила, приложенная к образцу для его разрыва.

Как и реометр типа Мейснера, реометр SER использует набор из двух роликов для деформации образца с заданной скоростью. ^[31] Затем он рассчитывает вязкость образца, используя известное уравнение: $\sigma =\eta {\dot {\epsilon }}$ где $\sigma$ это стресс, $\eta$ это вязкость и ${\dot {\epsilon }}$ это скорость деформации. Напряжение в этом случае определяется с помощью датчиков крутящего момента, имеющихся в приборе. Небольшой размер этого инструмента упрощает его использование и исключает провисание образца между роликами. Схему, подробно описывающую работу реометра растяжения SER, можно найти справа.

Другие методы

Хотя существует множество инструментов, которые проверяют механическую и вязкоупругую реакцию материалов, широкополосная вязкоупругая спектроскопия (BVS) и резонансная ультразвуковая спектроскопия (RUS) чаще используются для проверки вязкоупругого поведения, поскольку их можно использовать при температурах выше и ниже температуры окружающей среды и они более специфичны. для испытания вязкоупругости. Эти два инструмента используют механизм демпфирования на различных частотах и временных диапазонах без обращения к суперпозиции времени и температуры . Использование BVS и RUS для изучения механических свойств материалов важно для понимания того, как будет работать материал, обладающий вязкоупругостью. ^[32]

См. также

Ссылки

↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Мейерс и Чавла (1999): «Механическое поведение материалов», 98-103.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Маккрам, Бакли и Бакнелл (2003): «Принципы полимерной инженерии», 117–176.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Макоско, Кристофер В. (1994). Реология: принципы, измерения и приложения . Нью-Йорк: ВЧ. ISBN 978-1-60119-575-3 . OCLC 232602530 .
^ Бисвас, Абхиджит; Маниваннан, М.; Сринивасан, Мандьям А. (2015). «Многомасштабная многослойная биомеханическая модель тельца Пачини» . Транзакции IEEE на тактильных ощущениях . 8 (1): 31–42. дои : 10.1109/ТОХ.2014.2369416 . ПМИД 25398182 . S2CID 24658742 .
↑ Перейти обратно: Перейти обратно: ^а ^б Ван Влит, Кристин Дж. (2006). «3.032 Механическое поведение материалов»
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Какопардо, Людовика (январь 2019 г.). «Техническая вязкоупругость гидрогелей» . Журнал механического поведения биомедицинских материалов . 89 : 162–167. дои : 10.1016/j.jmbbm.2018.09.031 . hdl : 11568/930491 . ПМИД 30286375 . S2CID 52918639 – через Elsevier. Ошибка цитирования: именованная ссылка «:0» была определена несколько раз с разным содержимым (см. страницу справки ).
^ Ларсон, Рональд Г. (28 января 1999 г.). Структура и реология сложных жидкостей (темы химической инженерии): Ларсон, Рональд Г.: 9780195121971: Amazon.com: Books . Упс США. ISBN 019512197X .
^ Таннер, Роджер И. (1988). Инженерный реолог . Издательство Оксфордского университета. п. 27. ISBN 0-19-856197-0 .
^ Барнс, Ховард А.; Хаттон, Джон Флетчер; Уолтерс, К. (1989). Введение в реологию . Эльзевир. ISBN 978-0-444-87140-4 .
^ Берд, Р. Байрон (27 мая 1987 г.). Динамика полимерных жидкостей, Том 1: Механика жидкости . Уайли. ISBN 978-0-471-80245-7 .
^ Ройланс, Дэвид (2001); «Техническая вязкоупругость», 14–15.
^ Драпака, CS; Сивалоганатан, С.; Тенти, Г. (1 октября 2007 г.). «Нелинейные конститутивные законы вязкоупругости» . Математика и механика твердого тела . 12 (5): 475–501. дои : 10.1177/1081286506062450 . ISSN 1081-2865 . S2CID 121260529 .
^ Олдройд, Джеймс (февраль 1950 г.). «О формулировке реологических уравнений состояния». Труды Лондонского королевского общества. Серия А, Математические и физические науки . 200 (1063): 523–541. Бибкод : 1950RSPSA.200..523O . дои : 10.1098/rspa.1950.0035 . S2CID 123239889 .
^ Оуэнс, Р.Г.; Филлипс, Теннесси (2002). Вычислительная реология . Издательство Имперского колледжа. ISBN 978-1-86094-186-3 .
↑ Перейти обратно: Перейти обратно: ^а ^б Пул, Роб (октябрь 2007 г.). «Чисто упругие асимметрии течения». Письма о физических отзывах . 99 (16): 164503. Бибкод : 2007PhRvL..99p4503P . doi : 10.1103/PhysRevLett.99.164503 . hdl : 10400.6/634 . ПМИД 17995258 .
^ Вагнер, Манфред (1976). «Анализ зависимых от времени нелинейных данных о росте напряжений для сдвигового и удлиненного течения расплава разветвленного полиэтилена низкой плотности» . Реологика Акта . 15 (2): 136–142. дои : 10.1007/BF01517505 . S2CID 96165087 .
^ Вагнер, Манфред (1977). «Прогнозирование разницы первичных нормальных напряжений на основе данных о сдвиговой вязкости с использованием одного интегрального материального уравнения» . Реологика Акта . 16 (1977): 43–50. дои : 10.1007/BF01516928 . S2CID 98599256 .
^ Э. Дж. Барберо. «Принцип суперпозиции время-температура-возраст для прогнозирования долговременного реагирования линейных вязкоупругих материалов», глава 2 в книге « Ползучесть и усталость в композитах с полимерной матрицей» . Вудхед, 2011.
↑ Перейти обратно: Перейти обратно: ^а ^б Симулия. Руководство пользователя Abaqus Analysis , 19.7.1 «Викоупругость во временной области», версия 6.10, 2010 г.
^ Компьютерный предварительный выбор материала по единым стандартам
↑ Перейти обратно: Перейти обратно: ^а ^б Э. Дж. Барберо. Конечно-элементный анализ композиционных материалов . CRC Press, Бока-Ратон, Флорида, 2007 г.
^ С.А.Бёрле, А.Хотта, А.А.Гусев, Polymer 47 , 6243-6253 (2006).
^ Аклонис., Дж. Дж. (1981). «Механические свойства полимеров». J Chem Educ . 58 (11): 892. Бибкод : 1981ЖЧЭд..58..892А . дои : 10.1021/ed058p892 .
^ ИМ, Калогерас (2012). «Природа стеклообразного состояния: строение и стеклование». Журнал материального образования . 34 (3): 69.
^ Я, Эмри (2010). Временное поведение твердых полимеров .
^ Розато и др. (2001): «Справочник по проектированию пластмасс», 63–64.
^ Маньин, А.; Пиау, Дж. М. (1 января 1987 г.). «Сдвиговая реометрия жидкостей с пределом текучести» . Журнал механики неньютоновской жидкости . 23 : 91–106. Бибкод : 1987JNNFM..23...91M . дои : 10.1016/0377-0257(87)80012-5 . ISSN 0377-0257 .
↑ Перейти обратно: Перейти обратно: ^а ^б Дили, Дж. М. (1 января 1978 г.). «Растяжные реометры для расплавленных полимеров: обзор» . Журнал механики неньютоновской жидкости . 4 (1–2): 9–21. Бибкод : 1978JNNFM...4....9D . дои : 10.1016/0377-0257(78)85003-4 . ISSN 0377-0257 .
^ Мейснер, Дж.; Хостеттлер, Дж. (1 января 1994 г.). «Новый элонгационный реометр для расплавов полимеров и других высоковязкоупругих жидкостей» . Реологика Акта . 33 (1): 1–21. дои : 10.1007/BF00453459 . ISSN 1435-1528 . S2CID 93395453 .
^ Бах, Андерс; Расмуссен, Хенрик Коблиц; Хассагер, Оле (март 2003 г.). «Вязкость при растяжении расплавов полимеров, измеренная в реометре растяжения нити» . Журнал реологии . 47 (2): 429–441. Бибкод : 2003JRheo..47..429B . дои : 10.1122/1.1545072 . ISSN 0148-6055 . S2CID 44889615 .
^ Сентманат, Мартин Л. (1 декабря 2004 г.). «Миниатюрная универсальная испытательная платформа: от реологии растяжения расплава до поведения деформации твердого тела» . Реологика Акта . 43 (6): 657–669. дои : 10.1007/s00397-004-0405-4 . ISSN 1435-1528 . S2CID 73671672 .
^ Род Лейкс (1998). Вязкоупругие твердые вещества . ЦРК Пресс. ISBN 0-8493-9658-1 .

Силби и Альберти (2001): Физическая химия , 857. John Wiley & Sons, Inc.
Алан С. Вайнман и К.Р. Раджагопал (2000): Механическая реакция полимеров: введение
Аллен и Томас (1999): Структура материалов , 51.
Крандал и др. (1999): Введение в механику твердого тела 348.
Ж. Леметр и Ж.Л. Шабош (1994) Механика твердых материалов.
Ю. Димитриенко (2011) Нелинейная механика сплошной среды и большие неупругие деформации , Springer, 772p.

[Meyers-1] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Мейерс и Чавла (1999): «Механическое поведение материалов», 98-103.

[McCrum-2] Перейти обратно: Перейти обратно: ^а ^б ^с Маккрам, Бакли и Бакнелл (2003): «Принципы полимерной инженерии», 117–176.

[Macosko_1994-3] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Макоско, Кристофер В. (1994). Реология: принципы, измерения и приложения . Нью-Йорк: ВЧ. ISBN 978-1-60119-575-3 . OCLC 232602530 .

[4] Бисвас, Абхиджит; Маниваннан, М.; Сринивасан, Мандьям А. (2015). «Многомасштабная многослойная биомеханическая модель тельца Пачини» . Транзакции IEEE на тактильных ощущениях . 8 (1): 31–42. дои : 10.1109/ТОХ.2014.2369416 . ПМИД 25398182 . S2CID 24658742 .

[VanVliet-5] Перейти обратно: Перейти обратно: ^а ^б Ван Влит, Кристин Дж. (2006). «3.032 Механическое поведение материалов»

[:0-6] Перейти обратно: Перейти обратно: ^а ^б ^с Какопардо, Людовика (январь 2019 г.). «Техническая вязкоупругость гидрогелей» . Журнал механического поведения биомедицинских материалов . 89 : 162–167. дои : 10.1016/j.jmbbm.2018.09.031 . hdl : 11568/930491 . ПМИД 30286375 . S2CID 52918639 – через Elsevier. Ошибка цитирования: именованная ссылка «:0» была определена несколько раз с разным содержимым (см. страницу справки ).

[7] Ларсон, Рональд Г. (28 января 1999 г.). Структура и реология сложных жидкостей (темы химической инженерии): Ларсон, Рональд Г.: 9780195121971: Amazon.com: Books . Упс США. ISBN 019512197X .

[Tanner-8] Таннер, Роджер И. (1988). Инженерный реолог . Издательство Оксфордского университета. п. 27. ISBN 0-19-856197-0 .

[9] Барнс, Ховард А.; Хаттон, Джон Флетчер; Уолтерс, К. (1989). Введение в реологию . Эльзевир. ISBN 978-0-444-87140-4 .

[10] Берд, Р. Байрон (27 мая 1987 г.). Динамика полимерных жидкостей, Том 1: Механика жидкости . Уайли. ISBN 978-0-471-80245-7 .

[Roylance-11] Ройланс, Дэвид (2001); «Техническая вязкоупругость», 14–15.

[12] Драпака, CS; Сивалоганатан, С.; Тенти, Г. (1 октября 2007 г.). «Нелинейные конститутивные законы вязкоупругости» . Математика и механика твердого тела . 12 (5): 475–501. дои : 10.1177/1081286506062450 . ISSN 1081-2865 . S2CID 121260529 .

[a-13] Олдройд, Джеймс (февраль 1950 г.). «О формулировке реологических уравнений состояния». Труды Лондонского королевского общества. Серия А, Математические и физические науки . 200 (1063): 523–541. Бибкод : 1950RSPSA.200..523O . дои : 10.1098/rspa.1950.0035 . S2CID 123239889 .

[b-14] Оуэнс, Р.Г.; Филлипс, Теннесси (2002). Вычислительная реология . Издательство Имперского колледжа. ISBN 978-1-86094-186-3 .

[c-15] Перейти обратно: Перейти обратно: ^а ^б Пул, Роб (октябрь 2007 г.). «Чисто упругие асимметрии течения». Письма о физических отзывах . 99 (16): 164503. Бибкод : 2007PhRvL..99p4503P . doi : 10.1103/PhysRevLett.99.164503 . hdl : 10400.6/634 . ПМИД 17995258 .

[16] Вагнер, Манфред (1976). «Анализ зависимых от времени нелинейных данных о росте напряжений для сдвигового и удлиненного течения расплава разветвленного полиэтилена низкой плотности» . Реологика Акта . 15 (2): 136–142. дои : 10.1007/BF01517505 . S2CID 96165087 .

[17] Вагнер, Манфред (1977). «Прогнозирование разницы первичных нормальных напряжений на основе данных о сдвиговой вязкости с использованием одного интегрального материального уравнения» . Реологика Акта . 16 (1977): 43–50. дои : 10.1007/BF01516928 . S2CID 98599256 .

[ETT2011-18] Э. Дж. Барберо. «Принцип суперпозиции время-температура-возраст для прогнозирования долговременного реагирования линейных вязкоупругих материалов», глава 2 в книге « Ползучесть и усталость в композитах с полимерной матрицей» . Вудхед, 2011.

[Abaqus_Analysis_19.7.1-19] Перейти обратно: Перейти обратно: ^а ^б Симулия. Руководство пользователя Abaqus Analysis , 19.7.1 «Викоупругость во временной области», версия 6.10, 2010 г.

[campusplastics-20] Компьютерный предварительный выбор материала по единым стандартам

[Barbero2007-21] Перейти обратно: Перейти обратно: ^а ^б Э. Дж. Барберо. Конечно-элементный анализ композиционных материалов . CRC Press, Бока-Ратон, Флорида, 2007 г.

[22] С.А.Бёрле, А.Хотта, А.А.Гусев, Polymer 47 , 6243-6253 (2006).

[23] Аклонис., Дж. Дж. (1981). «Механические свойства полимеров». J Chem Educ . 58 (11): 892. Бибкод : 1981ЖЧЭд..58..892А . дои : 10.1021/ed058p892 .

[24] ИМ, Калогерас (2012). «Природа стеклообразного состояния: строение и стеклование». Журнал материального образования . 34 (3): 69.

[25] Я, Эмри (2010). Временное поведение твердых полимеров .

[Rosato-26] Розато и др. (2001): «Справочник по проектированию пластмасс», 63–64.

[27] Маньин, А.; Пиау, Дж. М. (1 января 1987 г.). «Сдвиговая реометрия жидкостей с пределом текучести» . Журнал механики неньютоновской жидкости . 23 : 91–106. Бибкод : 1987JNNFM..23...91M . дои : 10.1016/0377-0257(87)80012-5 . ISSN 0377-0257 .

[sciencedirect.com-28] Перейти обратно: Перейти обратно: ^а ^б Дили, Дж. М. (1 января 1978 г.). «Растяжные реометры для расплавленных полимеров: обзор» . Журнал механики неньютоновской жидкости . 4 (1–2): 9–21. Бибкод : 1978JNNFM...4....9D . дои : 10.1016/0377-0257(78)85003-4 . ISSN 0377-0257 .

[29] Мейснер, Дж.; Хостеттлер, Дж. (1 января 1994 г.). «Новый элонгационный реометр для расплавов полимеров и других высоковязкоупругих жидкостей» . Реологика Акта . 33 (1): 1–21. дои : 10.1007/BF00453459 . ISSN 1435-1528 . S2CID 93395453 .

[30] Бах, Андерс; Расмуссен, Хенрик Коблиц; Хассагер, Оле (март 2003 г.). «Вязкость при растяжении расплавов полимеров, измеренная в реометре растяжения нити» . Журнал реологии . 47 (2): 429–441. Бибкод : 2003JRheo..47..429B . дои : 10.1122/1.1545072 . ISSN 0148-6055 . S2CID 44889615 .

[31] Сентманат, Мартин Л. (1 декабря 2004 г.). «Миниатюрная универсальная испытательная платформа: от реологии растяжения расплава до поведения деформации твердого тела» . Реологика Акта . 43 (6): 657–669. дои : 10.1007/s00397-004-0405-4 . ISSN 1435-1528 . S2CID 73671672 .

[Lakes-32] Род Лейкс (1998). Вязкоупругие твердые вещества . ЦРК Пресс. ISBN 0-8493-9658-1 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]