Поверхностное натяжение

Чтобы узнать о рассказе Джеймса Блиша, см. « Поверхностное натяжение» (рассказ) .

Поток дождевой воды из навеса. Среди сил, управляющих образованием капель: поверхностное натяжение, сцепление , сила Ван-дер-Ваальса , неустойчивость Плато-Релея .

Продолжительность: 11 секунд. 0:11

взаимодействуют поверхностное натяжение и гидрофобность В этой попытке разрезать каплю воды .

Экспериментальная демонстрация поверхностного натяжения с мылом

Поверхностное натяжение — это тенденция покоящихся поверхностей жидкости сжиматься до минимально возможной площади поверхности . Поверхностное натяжение — это то, что позволяет объектам с более высокой плотностью, чем вода, таким как лезвия бритвы и насекомые (например, водомерки ), плавать на поверхности воды, не погружаясь даже частично.

На границе раздела жидкость-воздух поверхностное натяжение возникает в результате большего притяжения молекул жидкости друг к другу (из-за сцепления ), чем к молекулам в воздухе (из-за адгезии ).

В игре задействованы два основных механизма. Одним из них является внутренняя сила, действующая на поверхностные молекулы, заставляющая жидкость сжиматься. Во-вторых, это касательная сила, параллельная поверхности жидкости. Эту тангенциальную силу обычно называют поверхностным натяжением. Конечным эффектом является то, что жидкость ведет себя так, как если бы ее поверхность была покрыта натянутой эластичной мембраной. Но не следует заходить слишком далеко в этой аналогии, поскольку натяжение эластичной мембраны зависит от степени деформации мембраны, тогда как поверхностное натяжение является неотъемлемым свойством границы раздела жидкость - воздух или жидкость - пар.

Из-за относительно сильного притяжения молекул воды друг к другу через сеть водородных связей вода имеет более высокое поверхностное натяжение (72,8 миллиньютон (мН) на метр при 20 ° C), чем большинство других жидкостей. Поверхностное натяжение — важный фактор в явлении капиллярности .

Поверхностное натяжение имеет размерность силы энергии на единицу длины или единицу на площади . Эти два понятия эквивалентны, но, говоря об энергии на единицу площади, обычно используют термин « поверхностная энергия» , который является более общим термином в том смысле, что он применим также к твердым телам .

В материаловедении поверхностное натяжение используется либо для поверхностного напряжения , либо для поверхностной энергии .

Причины

Схема сил сцепления молекул жидкости

Из-за сил сцепления молекула, расположенная вдали от поверхности, притягивается одинаково во всех направлениях соседними молекулами жидкости, в результате чего результирующая сила равна нулю. Молекулы на поверхности не имеют одинаковых молекул со всех сторон и поэтому притягиваются внутрь. Это создает некоторое внутреннее давление и заставляет поверхности жидкости сжиматься до минимальной площади.

На границе раздела жидкость-воздух также существует напряжение, параллельное поверхности, которое будет сопротивляться внешней силе из-за когезионной природы молекул воды.

Силы притяжения, действующие между молекулами одного типа, называются силами сцепления, а силы, действующие между молекулами разных типов, — силами сцепления. Баланс между сцеплением жидкости и ее сцеплением с материалом емкости определяет степень смачивания , угол смачивания и форму мениска . При преобладании когезии (а именно, энергия адгезии составляет менее половины энергии когезии) смачивание невелико и мениск выпуклый у вертикальной стенки (как для ртути в стеклянной таре). С другой стороны, при преобладании адгезии (когда энергия адгезии превышает половину энергии сцепления) смачивание велико и аналогичный мениск вогнут (как в воде в стакане).

Поверхностное натяжение определяет форму капель жидкости. Хотя капли воды легко деформируются, они имеют тенденцию принимать сферическую форму из-за дисбаланса сил сцепления поверхностного слоя. В отсутствие других сил капли практически всех жидкостей имели бы примерно сферическую форму. Сферическая форма минимизирует необходимое «пристеночное натяжение» поверхностного слоя согласно закону Лапласа .

Капля воды лежит на дамаске . Поверхностное натяжение достаточно велико, чтобы предотвратить просачивание через ткань.

Другой способ рассматривать поверхностное натяжение — с точки зрения энергии. Молекула, контактирующая с соседом, находится в более низком энергетическом состоянии, чем если бы она была одна. Внутренние молекулы имеют столько соседей, сколько возможно, но у граничных молекул соседи отсутствуют (по сравнению с внутренними молекулами) и поэтому они имеют более высокую энергию. Чтобы жидкость минимизировала свое энергетическое состояние, необходимо минимизировать количество граничных молекул с более высокой энергией. Минимальное количество граничных молекул приводит к минимальной площади поверхности. В результате минимизации площади поверхности поверхность примет гладкую форму.

Физика

Физические единицы

Поверхностное натяжение, обозначаемое символом γ (альтернативно σ или T ), измеряется в силе на единицу длины . Единица измерения СИ — ньютон на метр, но единица СГС — дина также используется на сантиметр. Например,

$$\gamma =1~\mathrm {\frac {dyn}{cm}} =1~\mathrm {\frac {erg}{cm^{2}}} =1~\mathrm {\frac {10^{-7}\,m\cdot N}{10^{-4}\,m^{2}}} =0.001~\mathrm {\frac {N}{m}} =0.001~\mathrm {\frac {J}{m^{2}}} .$$

Определение

Эта диаграмма иллюстрирует силу, необходимую для увеличения площади поверхности. Эта сила пропорциональна поверхностному натяжению.

Поверхностное натяжение можно определить с точки зрения силы или энергии.

С точки зрения силы

Поверхностное натяжение γ жидкости — это сила на единицу длины. На рисунке справа прямоугольная рамка состоит из трех неподвижных сторон (черных), образующих U-образную форму, и четвертой подвижной стороны (синей), которая может сдвигаться вправо. Поверхностное натяжение потянет синюю полосу влево; сила F, необходимая для удержания подвижной стороны, пропорциональна длине L неподвижной стороны. Таким образом, соотношение F / L зависит только от внутренних свойств жидкости (состав, температура и т. д.), а не от ее геометрии. Например, если рама имела более сложную форму, соотношение F / L , где L — длина подвижной стороны, а F — сила, необходимая для предотвращения скольжения, оказывается одинаковой для всех форм. Поэтому мы определяем поверхностное натяжение как

$$\gamma ={\frac {F}{2L}}.$$

Причина 1/2 состоит в том , что пленка имеет две стороны (две поверхности), каждая из которых вносит равный вклад в силу; поэтому сила, вносимая одной стороной, равна γL = Ф / 2 .

С точки зрения энергетики

Поверхностное натяжение жидкости γ — это отношение изменения энергии жидкости к изменению площади поверхности жидкости (приведшему к изменению энергии). Это можно легко связать с предыдущим определением силы: если F — это сила, необходимая для того, чтобы сторона не начала скользить, то это также сила, которая удерживала бы сторону в состоянии скольжения с постоянной скоростью (согласно Второму закону Ньютона). Но если сторона движется вправо (в направлении приложения силы), то площадь поверхности растянутой жидкости увеличивается, пока приложенная сила совершает работу над жидкостью. Это означает, что увеличение площади поверхности увеличивает энергию пленки. совершаемая силой F при перемещении стороны на расстояние Δx , равна W = F Δx ; Работа , при этом общая площадь пленки увеличивается на Δ A = 2 L Δ x (здесь фактор 2, поскольку жидкость имеет две стороны, две поверхности). Таким образом, умножив числитель и знаменатель γ = 1 / 2 F / L на ∆x , получаем

$$\gamma ={\frac {F}{2L}}={\frac {F\Delta x}{2L\Delta x}}={\frac {W}{\Delta A}}.$$

Эта работа W , согласно обычным рассуждениям , интерпретируется как запасенная потенциальная энергия. Следовательно, поверхностное натяжение можно измерять также в системе СИ в джоулях на квадратный метр и в системе СГС в эргах на см. ² . Поскольку механические системы пытаются найти состояние минимальной потенциальной энергии , свободная капля жидкости естественным образом принимает сферическую форму, имеющую минимальную площадь поверхности для данного объема.Эквивалентность измерения энергии на единицу площади силе на единицу длины может быть доказана с помощью анализа размеров .

Эффекты

Вода

В обычной воде можно наблюдать несколько эффектов поверхностного натяжения:

1. Капли дождевой воды на восковой поверхности, например на листе. Вода слабо прилипает к воску и сильно к себе, поэтому вода скапливается в капли. Поверхностное натяжение придает им форму, близкую к сферической, поскольку сфера имеет наименьшее возможное соотношение площади поверхности к объему .
2. Образование капель происходит при растяжении массы жидкости. Анимация (ниже) показывает, как вода, прилипшая к крану, набирает массу, пока не растягивается до точки, в которой поверхностное натяжение больше не может удерживать каплю на кране. Затем она отделяется, и поверхностное натяжение формирует каплю в сферу. Если бы из крана текла струя воды, то при падении струя распалась бы на капли. Гравитация растягивает поток, а затем поверхностное натяжение сжимает его в сферы.
3. Плавание объектов плотнее воды происходит, когда объект несмачивается и его вес достаточно мал, чтобы выдерживать силы, возникающие из-за поверхностного натяжения. Например, водомерки используют поверхностное натяжение для передвижения по поверхности пруда следующим образом. Несмачиваемость ноги водомера означает, что между молекулами ноги и молекулами воды нет притяжения, поэтому, когда нога давит на воду, поверхностное натяжение воды пытается лишь восстановить ее плоскостность за счет ее деформации из-за нога. Такое поведение воды подталкивает водомерку вверх, поэтому он может стоять на поверхности воды, пока его масса достаточно мала, чтобы вода могла его поддерживать. Поверхность воды ведет себя как эластичная пленка: лапки насекомого оставляют углубления на поверхности воды, увеличивая ее площадь. а тенденция к минимизации кривизны поверхности (то есть площади) воды толкает ноги насекомого вверх.
4. Разделение масла и воды (в данном случае воды и жидкого воска) вызвано натяжением поверхности между разнородными жидкостями. Этот тип поверхностного натяжения называется «поверхностным натяжением», но его химический состав тот же.
5. Винные слезы – это образование капель и ручьев на стенках бокала с алкогольным напитком. Его причиной является сложное взаимодействие между различными поверхностными натяжениями воды и этанола ; это вызвано сочетанием модификации поверхностного натяжения воды этанолом и этанола, испаряющегося быстрее, чем вода.

• 
  A. Капли воды на листе
• 
  Б. Вода капает из крана
• 
  C. Водомерки остаются на поверхности жидкости из-за поверхностного натяжения.
• 
  D. Лава-лампа с взаимодействием разнородных жидкостей: воды и жидкого воска.
• 
  E. Фотография, демонстрирующая феномен « слез вина ».

Поверхностно-активные вещества

Поверхностное натяжение проявляется и в других распространенных явлениях, особенно когда поверхностно-активные вещества для его уменьшения используются :

• Мыльные пузыри имеют очень большую площадь поверхности при очень малой массе. Пузырьки в чистой воде нестабильны. Однако добавление поверхностно-активных веществ может оказать стабилизирующее воздействие на пузырьки (см. Эффект Марангони ). Поверхностно-активные вещества фактически снижают поверхностное натяжение воды в три и более раз.
• Эмульсии представляют собой разновидность коллоидных дисперсий, в которых важную роль играет поверхностное натяжение. Крошечные капли масла, диспергированные в чистой воде, самопроизвольно сливаются и разделяются на фазы. Добавление ПАВ снижает межфазное натяжение и способствует образованию капель нефти в водной среде (или наоборот). Стабильность таких образовавшихся капель нефти зависит от множества различных химических факторов и факторов окружающей среды.

поверхности

Силы поверхностного натяжения, действующие на крошечный (дифференциальный) участок поверхности. δθ _x и δθ _y указывают величину изгиба по размерам заплатки. Уравновешивание сил натяжения с давлением приводит к уравнению Юнга – Лапласа.

Если никакая сила не действует перпендикулярно натянутой поверхности, поверхность должна оставаться плоской. Но если давление на одной стороне поверхности отличается от давления на другой стороне, разница давлений, умноженная на площадь поверхности, дает нормальную силу. Чтобы силы поверхностного натяжения нейтрализовали силу давления, поверхность должна быть искривленной. На диаграмме показано, как кривизна крошечного участка поверхности приводит к тому, что результирующая составляющая сил поверхностного натяжения действует перпендикулярно центру участка. Когда все силы уравновешены, полученное уравнение известно как уравнение Юнга – Лапласа :

$$\Delta p=\gamma \left({\frac {1}{R_{x}}}+{\frac {1}{R_{y}}}\right)$$

где:

• Δp — разница давлений, известная как давление Лапласа .
• γ – поверхностное натяжение.
• R _x и R _y — радиусы кривизны по каждой из осей, параллельных поверхности.

Величина в скобках справа на самом деле (в два раза) равна средней кривизне поверхности (в зависимости от нормализации).Решения этого уравнения определяют форму капель воды, луж, менисков, мыльных пузырей и всех других форм, определяемых поверхностным натяжением (например, форму отпечатков ног водомера на поверхности пруда).В таблице ниже показано, как внутреннее давление капли воды увеличивается с уменьшением радиуса. Для не очень маленьких капель эффект незначителен, но разница давлений становится огромной, когда размеры капель приближаются к размерам молекул. (В пределах одной молекулы это понятие становится бессмысленным.)

Δp для капель воды разного радиуса на СТП

Радиус капли	1 мм	0,1 мм	1 мкм	10 нм
Δ р ( атм )	0.0014	0.0144	1.436	143.6

Плавающие объекты

См. Также: Плавучесть гибких объектов.

Поперечное сечение иглы, плавающей на поверхности воды. Fw _Fs — вес, а равнодействующая _— сила поверхностного натяжения.

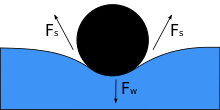
Когда объект помещается на жидкость, его вес F _w сжимает поверхность, и если поверхностное натяжение и нисходящая сила становятся равными, то он уравновешивается силами поверхностного натяжения с обеих сторон F _s , каждая из которых параллельна поверхности воды в точке точки контакта с объектом. Обратите внимание, что небольшое движение тела может привести к тому, что предмет утонет. По мере уменьшения угла контакта поверхностное натяжение уменьшается. Горизонтальные компоненты двух F _{стрелок} указывают в противоположных направлениях, поэтому они компенсируют друг друга, но вертикальные компоненты указывают в одном направлении и, следовательно, складываются. для баланса F _w . Чтобы это произошло, поверхность объекта не должна быть смачиваемой, а его вес должен быть достаточно низким, чтобы поверхностное натяжение могло его выдержать. Если m обозначает массу иглы, а g — ускорение силы тяжести, мы имеем

$$F_{\mathrm {w} }=2F_{\mathrm {s} }\sin \theta \quad \Leftrightarrow \quad mg=2\gamma L\sin \theta$$

Жидкая поверхность

Минимальная поверхность

Найти форму минимальной поверхности, ограниченной некоторой рамкой произвольной формы, используя строго математические методы, может оказаться непростой задачей. Тем не менее, если сделать каркас из проволоки и окунуть его в мыльный раствор, в полученной мыльной пленке за считанные секунды появится локально минимальная поверхность.

Причина этого в том, что разница давлений на границе раздела жидкости пропорциональна средней кривизне , как видно из уравнения Янга-Лапласа . Для открытой мыльной пленки разница давлений равна нулю, следовательно, средняя кривизна равна нулю, а минимальные поверхности обладают свойством нулевой средней кривизны.

Углы контакта

Основная статья: Угол контакта

Поверхность любой жидкости является границей раздела между этой жидкостью и какой-либо другой средой. Например, верхняя поверхность пруда представляет собой границу между водой в пруду и воздухом. Таким образом, поверхностное натяжение является свойством не только жидкости, но и свойством границы раздела жидкости с другой средой. Если жидкость находится в контейнере, то помимо границы раздела жидкость/воздух на его верхней поверхности имеется еще граница раздела между жидкостью и стенками контейнера. Поверхностное натяжение между жидкостью и воздухом обычно отличается (больше), чем ее поверхностное натяжение со стенками сосуда. А там, где встречаются две поверхности, их геометрия должна быть такой, чтобы все силы уравновешивались.

Силы в точке контакта показаны для угла контакта больше 90° (слева) и меньше 90° (справа).

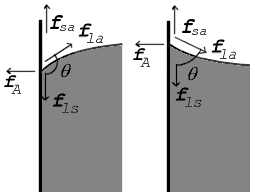Там, где две поверхности встречаются, они образуют контакта угол θ , который представляет собой угол, который касательная к поверхности образует с твердой поверхностью. Обратите внимание, что угол измеряется через жидкость , как показано на диаграммах выше. На диаграмме справа показаны два примера. Силы растяжения показаны для границы раздела жидкость-воздух, границы жидкость-твердое тело и границы раздела твердое тело-воздух. В примере слева показано, что разница между поверхностным натяжением жидкость-твердое тело и твердое тело-воздух, γ _ls − γ _sa , меньше, чем поверхностное натяжение жидкость-воздух, γ _la , но, тем не менее, положительна, то есть

$$\gamma _{\mathrm {la} }>\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }>0$$

На диаграмме как вертикальная, так и горизонтальная силы должны компенсироваться точно в точке контакта, известной как равновесие . Горизонтальная составляющая f _la компенсируется силой сцепления f _A .

$$f_{\mathrm {A} }=f_{\mathrm {la} }\sin \theta$$

Однако более показательный баланс сил наблюдается в вертикальном направлении. Вертикальная составляющая f _la должна точно компенсировать разницу сил вдоль твердой поверхности f _ls − f _sa .

$$f_{\mathrm {ls} }-f_{\mathrm {sa} }=-f_{\mathrm {la} }\cos \theta$$

Некоторые углы контакта жидкость-твердое тело

Жидкость	Твердый	Контакт угол
вода	натриево-известковое стекло свинцовое стекло плавленый кварц	0°
этанол
диэтиловый эфир
четыреххлористый углерод
глицерин
уксусная кислота
вода	парафиновый воск	107°
	серебро	90°
йодистый метил	натриево-известковое стекло	29°
	свинцовое стекло	30°
	плавленый кварц	33°
Меркурий	натриево-известковое стекло	140°

Поскольку силы прямо пропорциональны их поверхностному натяжению, мы также имеем:

$$\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }=-\gamma _{\mathrm {la} }\cos \theta$$

где

• γ _ls – поверхностное натяжение жидкость–твердое тело,
• γ _la – поверхностное натяжение жидкость–воздух,
• γ _sa – поверхностное натяжение твердое тело–воздух,
• θ - угол контакта, при этом вогнутый мениск имеет угол контакта менее 90 °, а выпуклый мениск имеет угол контакта более 90 °.

Это означает, что, хотя разницу между поверхностным натяжением жидкость-твердое тело и твердое тело-воздух, γ _ls − γ _sa , трудно измерить напрямую, ее можно вывести из поверхностного натяжения жидкость-воздух, γ _la , и равновесного угла смачивания. , θ , который является функцией легко измеримых углов контакта при наступлении и отступлении (см. угол контакта в основной статье ).

Такая же связь существует и на диаграмме справа. Но в этом случае мы видим, что, поскольку угол контакта меньше 90 °, разность поверхностного натяжения жидкость-твердое тело/твердое тело-воздух должна быть отрицательной:

$$\gamma _{\mathrm {la} }>0>\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }$$

Специальные углы контакта

Обратите внимание, что в частном случае границы раздела вода-серебро, где угол контакта равен 90 °, разница поверхностного натяжения жидкость-твердое тело/твердое тело-воздух равна точно нулю.

Другой особый случай — угол контакта ровно 180°. Подходит для этого вода со специально подготовленным тефлоном . Угол контакта 180 ° возникает, когда поверхностное натяжение жидкость-твердое тело точно равно поверхностному натяжению жидкость-воздух.

$$\gamma _{\mathrm {la} }=\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }>0\qquad \theta =180^{\circ }$$

Жидкость в вертикальной трубке

Основная статья: Капиллярное действие

Схема ртутного барометра

старого образца Ртутный барометр состоит из вертикальной стеклянной трубки диаметром около 1 см, частично заполненной ртутью, и вакуума (так называемого вакуума Торричелли ) в незаполненном объеме (см. схему справа). Обратите внимание, что уровень ртути в центре трубки выше, чем по краям, поэтому верхняя поверхность ртутной трубки имеет куполообразную форму. Центр массы всего столба ртути был бы немного ниже, если бы верхняя поверхность ртути была плоской по всему поперечному сечению трубки. Но куполообразная вершина дает чуть меньшую площадь поверхности всей массе ртути. И снова эти два эффекта объединяются, чтобы минимизировать общую потенциальную энергию. Такая форма поверхности известна как выпуклый мениск.

Мы рассматриваем площадь поверхности всей массы ртути, включая ту часть поверхности, которая соприкасается со стеклом, поскольку ртуть вообще не прилипает к стеклу. Таким образом, поверхностное натяжение ртути действует на всю площадь ее поверхности, в том числе и там, где она соприкасается со стеклом. Если бы вместо стекла трубка была сделана из меди, ситуация была бы совсем иной. Ртуть агрессивно прилипает к меди. Так в медной трубке уровень ртути в центре трубки будет ниже, чем по краям (т. е. это будет вогнутый мениск). В ситуации, когда жидкость прилипает к стенкам контейнера, мы считаем, что часть площади поверхности жидкости, контактирующая с контейнером, имеет отрицательное поверхностное натяжение. Затем жидкость работает над максимизацией площади контактной поверхности. Таким образом, в этом случае увеличение площади контакта с контейнером уменьшает, а не увеличивает потенциальную энергию. Этого уменьшения достаточно, чтобы компенсировать возросшую потенциальную энергию, связанную с подъемом жидкости у стенок контейнера.

Иллюстрация капиллярного подъема и падения. Красный = угол контакта менее 90°; синий = угол контакта более 90°

Если трубка достаточно узкая и прилипание жидкости к ее стенкам достаточно сильное, поверхностное натяжение может поднять жидкость вверх по трубке в результате явления, известного как капиллярное действие . Высота, на которую поднимается колонна, определяется законом Жюрина :

$$h={\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}$$

где

• h — высота, на которую поднимается жидкость,
• γ _la – поверхностное натяжение жидкость–воздух,
• ρ — плотность жидкости,
• r – радиус капилляра,
• g - ускорение свободного падения,
• θ – угол контакта, описанный выше. Если угол θ больше 90°, как в случае с ртутью в стеклянном контейнере, жидкость будет опускаться, а не подниматься.

Лужи на поверхности

Кривая профиля края лужи при угле контакта 180°. Кривая задается формулой:

$$x-x_{0}={\frac {1}{2}}H\cosh ^{-1}\left({\frac {H}{h}}\right)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}$$

где ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$

Небольшие лужицы воды на гладкой чистой поверхности имеют ощутимую толщину.

Если налить ртуть на горизонтальный плоский лист стекла, образуется лужа ощутимой толщины. Лужа растечется лишь до того момента, пока ее толщина не станет чуть меньше полсантиметра и не тоньше. Опять же, это происходит из-за действия сильного поверхностного натяжения ртути. Жидкая масса выравнивается, потому что при этом максимально возможное количество ртути снижается, но поверхностное натяжение в то же время уменьшает общую площадь поверхности. Результатом компромисса является лужа почти фиксированной толщины.

Такую же демонстрацию поверхностного натяжения можно провести с водой, известковой водой или даже физиологическим раствором, но только на поверхности, состоящей из вещества, к которому вода не прилипает. Воск является таким веществом. Вода, вылитая на гладкую, плоскую, горизонтальную восковую поверхность, скажем, на вощеный лист стекла, будет вести себя аналогично ртути, вылитой на стекло.

Толщина лужи жидкости на поверхности с углом контакта 180° определяется по формуле:

$$h=2{\sqrt {\frac {\gamma }{g\rho }}}$$

где

• h — глубина лужи в сантиметрах или метрах.
• γ — поверхностное натяжение жидкости в динах на сантиметр или ньютонах на метр.
• g — ускорение свободного падения, равное 980 см/с. ² или 9,8 м/с ²
• ρ — плотность жидкости в граммах на кубический сантиметр или килограммах на кубический метр.

Иллюстрация того, как меньший угол контакта приводит к уменьшению глубины лужи

В действительности толщина луж будет немного меньше, чем предсказывает приведенная выше формула, поскольку очень немногие поверхности имеют угол контакта с любой жидкостью 180°. Если угол контакта меньше 180°, толщина определяется по формуле:

$$h={\sqrt {\frac {2\gamma _{\mathrm {la} }\left(1-\cos \theta \right)}{g\rho }}}.$$

Для ртути на стекле γ _Hg = 487 дин/см, ρ _Hg = 13,5 г/см. ³ и θ = 140°, что дает h _Hg = 0,36 см. Для воды на парафине при 25 °С γ = 72 дин/см, ρ = 1,0 г/см. ³ , и θ = 107°, что дает h _{H 2 O} = 0,44 см.

Формула также предсказывает, что когда угол контакта равен 0°, жидкость будет распространяться микротонким слоем по поверхности. Говорят, что такая поверхность полностью смачивается жидкостью.

Распад потоков на капли

Разрушение вытянутой струи воды на капли за счет поверхностного натяжения.

Основная статья: Неустойчивость Плато – Рэлея

В повседневной жизни все мы наблюдаем, что струя воды, выходящая из крана, распадается на капли, независимо от того, насколько плавно струя вытекает из крана. Это происходит из-за явления, называемого неустойчивостью Плато-Релея . что полностью является следствием воздействия поверхностного натяжения.

Объяснение этой неустойчивости начинается с существования крошечных возмущений в потоке. Они всегда присутствуют, каким бы плавным ни был поток. Если возмущения разложить на синусоидальные компоненты, мы обнаружим, что некоторые компоненты со временем растут, а другие со временем затухают. Среди тех, которые растут со временем, некоторые растут быстрее, чем другие. Распадается или растет компонент, а также скорость его роста полностью зависит от его волнового числа (меры количества пиков и впадин на сантиметр) и радиусов исходного цилиндрического потока.

Галерея

• 
  Разрушение движущегося слоя воды, отскакивающего от ложки.
• 
  Фотография текущей воды, прилипшей к руке. Поверхностное натяжение создает слой воды между потоком и рукой.
• 
  Мыльный пузырь уравновешивает силы поверхностного натяжения и внутреннего пневматического давления .
• 
  Поверхностное натяжение предотвращает погружение монеты: монета, несомненно, плотнее воды, поэтому она должна вытеснять больший объем, чем ее собственный, чтобы плавучесть уравновешивала массу.
• 
  Алюминиевая монета плавает на поверхности воды при температуре 10°С. Любой дополнительный вес упадет монету на дно.
• 
  Ромашка. Весь цветок лежит ниже уровня (ненарушенной) свободной поверхности. Вода плавно поднимается по краю. Поверхностное натяжение не позволяет воде вытеснить воздух между лепестками и, возможно, затопить цветок.
• 
  Металлическая скрепка плавает в воде. Обычно можно осторожно добавить несколько штук, не допуская перелива воды.
• 
  Металлическая скрепка, плавающая на воде. Решетка перед источником света создала «контурные линии», которые показывают деформацию поверхности воды, вызванную металлической скрепкой.

Термодинамика

Термодинамические теории поверхностного натяжения

Дж. У. Гиббс разработал термодинамическую теорию капиллярности, основанную нана идее поверхностей разрыва. Гиббс рассмотрел случай, когда четкая математическая поверхность помещается где-то внутри микроскопически нечеткой физической границы раздела, существующей между двумя однородными веществами. Понимая, что точный выбор местоположения поверхности несколько произволен, он оставил его гибким. Поскольку граница раздела существует в тепловом и химическом равновесии с веществами вокруг нее (имеющими температуру T и химические потенциалы μ _i ), Гиббс рассмотрел случай, когда поверхность может иметь избыточную энергию, избыточную энтропию и избыточные частицы, найдя естественную функцию свободной энергии в этом случае быть $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$, величина, позже названная большим потенциалом и получившая символ $\Omega$.

Размещение Гиббсом точной математической поверхности в нечетком физическом интерфейсе.

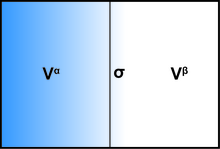
Учитывая данный подобъем $V$ содержащая поверхность разрыва, объем делится математической поверхностью на две части A и B, причем объемы $V_{\text{A}}$ и $V_{\text{B}}$, с $V=V_{\text{A}}+V_{\text{B}}$ точно. Теперь, если бы две части A и B были однородными жидкостями (с давлением $p_{\text{A}}$, $p_{\text{B}}$) и оставался совершенно однородным вплоть до математической границы, без каких-либо поверхностных эффектов, общий грандиозный потенциал этого объема был бы просто $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$. Интересующие поверхностные эффекты являются модификацией этого, и все они могут быть объединены в термин свободной поверхностной энергии. $\Omega _{\text{S}}$ таким образом, общий потенциал объема составит:

$$\Omega =-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}+\Omega _{\text{S}}.$$

Для достаточно макроскопических и слегка изогнутых поверхностей поверхностная свободная энергия должна быть просто пропорциональна площади поверхности:

$$\Omega _{\text{S}}=\gamma A,$$

по поверхностному натяжению $\gamma$ и площадь поверхности $A$.

Как указано выше, это означает, что механическая работа, необходимая для увеличения площади поверхности A, равна dW = γ dA , при условии, что объемы с каждой стороны не меняются. Термодинамика требует, чтобы для систем, находящихся при постоянных химическом потенциале и температуре, все спонтанные изменения состояния сопровождались уменьшением этой свободной энергии. $\Omega$, то есть увеличение полной энтропии с учетом возможного перемещения энергии и частиц с поверхности в окружающие жидкости. Отсюда легко понять, почему уменьшение площади поверхности массы жидкости всегда происходит самопроизвольно , если только оно не связано с какими-либо другими изменениями энергии. Отсюда следует, что для увеличения площади поверхности необходимо приложить определенное количество энергии.

Гиббс и другие ученые боролись с произвольностью точного микроскопического расположения поверхности. Для микроскопических поверхностей с очень большой кривизной неверно предполагать, что поверхностное натяжение не зависит от размера, и такие темы, как длина Толмена в игру вступают . Для поверхности макроскопического размера (и плоских поверхностей) расположение поверхности не оказывает существенного влияния на γ ; однако он оказывает очень сильное влияние на значения поверхностной энтропии, плотности поверхностной избыточной массы и внутренней энергии поверхности. которые являются частными производными функции поверхностного натяжения $\gamma (T,\mu _{1},\mu _{2},\cdots )$.

Гиббс подчеркнул, что для твердых тел поверхностная свободная энергия может полностью отличаться от поверхностного напряжения (то, что он назвал поверхностным натяжением): свободная поверхностная энергия — это работа, необходимая для образования поверхности, а поверхностное напряжение — это работа, необходимая для растяжения поверхности. В случае границы раздела двух жидкостей нет различия между формованием и растяжением, поскольку жидкости и поверхность полностью восстанавливают свою природу при растяжении поверхности. Для твердого тела растяжение поверхности, даже упругое, приводит к фундаментальному изменению поверхности. Кроме того, поверхностное напряжение твердого тела представляет собой направленную величину ( тензор напряжений ), а поверхностная энергия скалярна.

Через пятнадцать лет после Гиббса Дж. Д. Ван дер Ваальс разработал теорию капиллярных эффектов, основанную на гипотезе непрерывного изменения плотности. Он добавил к плотности энергии член $c(\nabla \rho )^{2},$ где c — коэффициент капиллярности, ρ — плотность. Для многофазных равновесий результаты подхода Ван-дер-Ваальса практически совпадают с формулами Гиббса, но для моделирования динамики фазовых переходов подход Ван-дер-Ваальса гораздо удобнее. Капиллярная энергия Ван-дер-Ваальса в настоящее время широко используется в моделях фазового поля многофазных потоков. Подобные члены обнаружены и в динамике неравновесных газов.

Термодинамика пузырьков

Давление внутри идеального сферического пузыря можно определить из термодинамических соображений свободной энергии. Вышеупомянутую свободную энергию можно записать как:

$$\Omega =-\Delta PV_{\text{A}}-p_{\text{B}}V+\gamma A$$

где $\Delta P=p_{\text{A}}-p_{\text{B}}$ - это разница давлений между внутренней (A) и внешней (B) пузырьком, и $V_{\text{A}}$ - объем пузырька. В равновесии d Ω = 0 и, следовательно,

$$\Delta P\,dV_{\text{A}}=\gamma \,dA.$$

Для сферического пузыря объем и площадь поверхности определяются просто как

$$V_{\text{A}}={\tfrac {4}{3}}\pi R^{3}\quad \rightarrow \quad dV_{\text{A}}=4\pi R^{2}\,dR,$$

и

$$A=4\pi R^{2}\quad \rightarrow \quad dA=8\pi R\,dR.$$

Подставляя эти соотношения в предыдущее выражение, находим

$$\Delta P={\frac {2}{R}}\gamma ,$$

что эквивалентно уравнению Юнга – Лапласа , когда R _x = R _y .

Влияние температуры

Температурная зависимость поверхностного натяжения между жидкой и паровой фазами чистой воды

Температурная зависимость поверхностного натяжения бензола

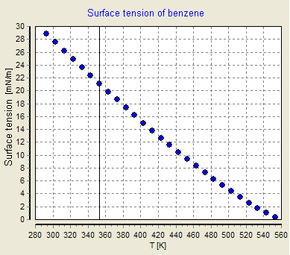
Поверхностное натяжение зависит от температуры. По этой причине, когда указывается значение поверхностного натяжения границы раздела, температура должна быть явно указана. Общая тенденция такова, что поверхностное натяжение уменьшается с повышением температуры, достигая значения 0 при критической температуре . Более подробную информацию см. в правиле Этвеша . Существуют только эмпирические уравнения, связывающие поверхностное натяжение и температуру:

• Этвёш:
  $$\gamma V^{2/3}=k(T_{\mathrm {C} }-T).$$
  Здесь V — мольный объем вещества, T _C — критическая температура , а k — константа, справедливая почти для всех веществ. Типичное значение k = 2,1 × 10. ⁻⁷ Дж.К. ⁻¹ моль ^{− 2 ⁄ 3} . Для воды можно дополнительно использовать V = 18 мл/моль и T _C = 647 К (374 °С). Вариант Этвоса описан Рамаем и Шилдсом:
  $$\gamma V^{2/3}=k\left(T_{\mathrm {C} }-T-6\,\mathrm {K} \right)$$
  где температурное смещение на 6 К обеспечивает лучшее соответствие формулы реальности при более низких температурах.
• Гуггенхайм-Катаяма:
  $$\gamma =\gamma ^{\circ }\left(1-{\frac {T}{T_{\mathrm {C} }}}\right)^{n}$$
  γ ° — константа для каждой жидкости, а n — эмпирический коэффициент, значение которого равно 11/9 для органических жидкостей . Это уравнение было также предложено Ван дер Ваальсом , который далее предположил, что γ ° может быть задано выражением
  $$K_{2}T_{\mathrm {C} }^{1/3}P_{\mathrm {C} }^{2/3},$$
  где K ₂ — универсальная константа для всех жидкостей, а PC _— критическое давление жидкости (хотя более поздние эксперименты показали, что K ₂ в некоторой степени варьируется от одной жидкости к другой).

И Гуггенхайм-Катаяма, и Этвос принимают во внимание тот факт, что поверхностное натяжение достигает 0 при критической температуре, тогда как Рамай и Шилдс не могут соответствовать реальности в этой конечной точке.

концентрации

Растворенные вещества могут оказывать различное влияние на поверхностное натяжение в зависимости от природы поверхности и растворенного вещества:

• Незначительный эффект или его отсутствие, например, сахар в воде/воздухе, большинство органических соединений в масле/воздухе.
• Увеличивает поверхностное натяжение большинства неорганических солей в воде|воздухе.
• Немонотонное изменение большинства неорганических кислот в воде|воздухе.
• Постепенно уменьшайте поверхностное натяжение, как и у большинства амфифилов, например спиртов в воде|воздухе.
• Уменьшайте поверхностное натяжение до достижения определенной критической концентрации, а потом никакого эффекта: поверхностно-активные вещества , образующие мицеллы.

Эффект усложняется тем, что растворенное вещество может существовать в другой концентрации на поверхности растворителя, чем в его объеме. Эта разница варьируется от одной комбинации растворенного вещества к другой.

Изотерма Гиббса утверждает, что:

$$\Gamma =-{\frac {1}{RT}}\left({\frac {\partial \gamma }{\partial \ln C}}\right)_{T,P}$$

• Γ известен как поверхностная концентрация. Он представляет собой избыток растворенного вещества на единицу площади поверхности по сравнению с тем, который присутствовал бы, если бы объемная концентрация преобладала на всем пути к поверхности. Имеет единицы измерения моль/м. ²
• С – концентрация вещества в объемном растворе.
• R — газовая постоянная , а T — температура .

При его выводе принимаются определенные допущения, поэтому изотерму Гиббса можно применять только к идеальным (очень разбавленным) растворам с двумя компонентами.

Влияние размера частиц на давление пара

Смотрите также: эффект Гиббса – Томсона.

Соотношение Клаузиуса -Клапейрона приводит к другому уравнению, также приписываемому Кельвину, как уравнение Кельвина . Это объясняет, почему из-за поверхностного натяжения давление пара для небольших капель жидкости в суспензии превышает стандартное давление пара той же жидкости, когда граница раздела плоская. Другими словами, когда жидкость образует маленькие капли, равновесная концентрация ее пара в окружающей среде больше. Это возникает потому, что давление внутри капли больше, чем снаружи.

$$P_{\mathrm {v} }^{\mathrm {fog} }=P_{\mathrm {v} }^{\circ }e^{V2\gamma /(RTr_{\mathrm {k} })}$$

Молекулы на поверхности крошечной капли (слева) имеют в среднем меньше соседей, чем молекулы на плоской поверхности (справа). Следовательно, они слабее связаны с каплей, чем молекулы с плоской поверхностью.

• P _v ° — стандартное давление пара этой жидкости при данной температуре и давлении.
• V – молярный объем.
• R — газовая постоянная
• r _k – радиус Кельвина, радиус капли.

Эффект объясняет пересыщение паров. В отсутствие мест зародышеобразования должны образоваться крошечные капли, прежде чем они смогут превратиться в более крупные капли. Для этого требуется давление пара, во много раз превышающее давление пара в точке фазового перехода .

Это уравнение также используется в химии катализаторов для оценки мезопористости твердых веществ.

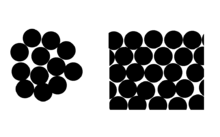
Эффект можно рассматривать с точки зрения среднего числа молекулярных соседей поверхностных молекул (см. Диаграмму).

В таблице приведены некоторые расчетные значения этого эффекта для воды при разных размерах капель:

P / P 0 для капель воды разного радиуса на СТП
Радиус капли (нм)	1000	100	10	1
П / П 0	1.001	1.011	1.114	2.95

Эффект становится очевидным для капель очень малого размера, поскольку в капле радиусом 1 нм содержится около 100 молекул, а это количество достаточно мало, чтобы потребовать квантовомеханического анализа.

Методы измерения

Поскольку поверхностное натяжение проявляется в различных эффектах, оно предлагает несколько путей его измерения. Какой метод является оптимальным, зависит от природы измеряемой жидкости, условий, при которых необходимо измерять ее натяжение, и устойчивости ее поверхности при ее деформации. Прибор, измеряющий поверхностное натяжение, называется тензиометром.

• Метод кольца Дю Нуи : традиционный метод, используемый для измерения поверхностного или межфазного натяжения. Смачивающие свойства поверхности или границы раздела мало влияют на этот метод измерения. Измеряется максимальное усилие, действующее на кольцо со стороны поверхности.
• Метод пластины Вильгельми : универсальный метод, особенно подходящий для проверки поверхностного натяжения в течение длительных интервалов времени. Вертикальную пластину известного периметра прикрепляют к весам и измеряют силу, возникающую при смачивании.
• Метод вращающейся капли : этот метод идеально подходит для измерения низкого межфазного натяжения. Диаметр капли тяжелой фазы измеряется при вращении обеих капель.
• Метод подвесной капли : с помощью этого метода можно измерить поверхностное и межфазное натяжение даже при повышенных температурах и давлениях. Геометрия капли анализируется оптически. Для висячих капель максимальный диаметр и соотношение этого параметра и диаметра на расстоянии максимального диаметра от вершины капли использовались для оценки параметров размера и формы с целью определения поверхностного натяжения.
• Метод давления пузырьков (метод Егера): метод измерения для определения поверхностного натяжения при небольшом возрасте поверхности. Измеряют максимальное давление каждого пузырька.
• Метод объема капли: метод определения межфазного натяжения в зависимости от возраста интерфейса. Жидкость одной плотности перекачивают во вторую жидкость другой плотности и измеряют время между образованием капель.
• Метод капиллярного подъема: конец капилляра погружают в раствор. Высота, на которой раствор попадает внутрь капилляра, связана с поверхностным натяжением уравнением, обсуждавшимся выше .
• Сталагмометрический метод : метод взвешивания и измерения капли жидкости.
• Метод сидячей капли : метод определения поверхностного натяжения и плотности путем помещения капли на подложку и измерения угла контакта (см. Техника сидячей капли ).
• Метод Дю Нуи – Паддея : в минимизированной версии метода Дю Нуи вместо кольца используется металлическая игла небольшого диаметра в сочетании с высокочувствительными микровесами для регистрации максимального натяжения. Преимущество этого метода состоит в том, что очень малые объемы пробы (до нескольких десятков микролитров) можно измерить с очень высокой точностью без необходимости поправки на плавучесть (для иглы или, скорее, стержня с правильной геометрией). Кроме того, измерение можно выполнить очень быстро, минимум примерно за 20 секунд.
• Частота колебаний левитирующих капель. Собственная частота колебательных колебаний капель, левитирующих на магните, использовалась для измерения поверхностного натяжения сверхтекучих жидкостей. ⁴ Он. Это значение оценивается в 0,375 дин/см при Т = 0 К.
• Резонансные колебания сферических и полусферических капель жидкости. Метод основан на измерении резонансной частоты сферических и полусферических висячих капель, приводимых в колебания модулированным электрическим полем. По полученным резонансным кривым можно оценить поверхностное натяжение и вязкость.
• Метод падения-отскока: этот метод основан на аэродинамической левитации с разъемной конструкцией сопла. После падения стабильно левитирующей капли на платформу образец деформируется и отскакивает назад, колеблясь в воздухе, пытаясь минимизировать площадь своей поверхности. Благодаря такому колебательному поведению можно измерить поверхностное натяжение и вязкость жидкости.

Ценности

Таблица данных

Поверхностное натяжение различных жидкостей в дин /см по отношению к воздуху
Составы смесей, обозначенные «%», даны по массе.
дин/см эквивалентен единицам СИ мН/м (миллиньютон на метр).

Жидкость	Температура (°С)	Поверхностное натяжение, с
Уксусная кислота	20	27.60
Уксусная кислота (45,1%) + Вода	30	40.68
Уксусная кислота (10,0%) + Вода	30	54.56
Ацетон	20	23.70
Кровь	22	55.89
Диэтиловый эфир	20	17.00
Этанол	20	22.27
Этанол (40%) + Вода	25	29.63
Этанол (11,1%) + Вода	25	46.03
Глицерин	20	63.00
н -Гексан	20	18.40
Соляная кислота 17,7 М водный раствор	20	65.95
изопропанол	20	21.70
Жидкий гелий II	−273	0.37
Жидкий азот	−196	8.85
Жидкий кислород	−182	13.2
Меркурий	15	487.00
Метанол	20	22.60
Расплавленный хлорид серебра	650	163
Расплавленный хлорид натрия / хлорид кальция (47/53 мол. %)	650	139
н -октан	20	21.80
Хлорид натрия 6,0 М водный раствор	20	82.55
Сахароза (55%) + вода	20	76.45
Вода	0	75.64
Вода	25	71.97
Вода	50	67.91
Вода	100	58.85
Толуол	25	27.73

Поверхностное натяжение воды

Поверхностное натяжение чистой жидкой воды при контакте с ее парами определено IAPWS. как

$$\gamma _{\text{w}}=235.8\left(1-{\frac {T}{T_{\text{C}}}}\right)^{1.256}\left[1-0.625\left(1-{\frac {T}{T_{\text{C}}}}\right)\right]~{\text{mN/m}},$$

где и T , и критическая температура TC _{= 647,096 К} выражены в кельвинах . Область действия — вся кривая парожидкостного насыщения от тройной точки (0,01 °С) до критической точки. Он также дает разумные результаты при экстраполяции на метастабильные (переохлажденные) условия, по крайней мере, до -25 ° C. Эта формулировка была первоначально принята IAPWS в 1976 году и скорректирована в 1994 году для соответствия Международной температурной шкале 1990 года.

Неопределенность этой формулировки определяется IAPWS во всем диапазоне температур. Для температур ниже 100 °C погрешность составляет ±0,5%.

Поверхностное натяжение морской воды

Наяр и др. опубликованные справочные данные по поверхностному натяжению морской воды в диапазоне солености 20 ≤ S ≤ 131 г/кг и диапазоне температур 1 ≤ t ≤ 92 °C при атмосферном давлении. Диапазон температур и солености охватывает как океанографический диапазон, так и диапазон условий, встречающихся в термического опреснения технологиях . Погрешность измерений варьировалась от 0,18 до 0,37 мН/м при средней погрешности 0,22 мН/м.

Наяр и др. сопоставил данные со следующим уравнением

$$\gamma _{\mathrm {sw} }=\gamma _{\mathrm {w} }\left(1+3.766\times 10^{-4}S+2.347\times 10^{-6}St\right)$$

где γ _sw — поверхностное натяжение морской воды в мН/м, γ _w — поверхностное натяжение воды в мН/м, S — эталонная соленость. в г/кг, а t — температура в градусах Цельсия. Среднее абсолютное процентное отклонение между измерениями и корреляцией составило 0,19%, а максимальное отклонение — 0,60%.

Международная ассоциация свойств воды и пара (IAPWS) приняла эту корреляцию в качестве международного стандарта.

См. также

• Антизуб
• Капиллярная волна — короткие волны на поверхности воды, обусловленные поверхностным натяжением и инерцией.
• Эффект Cheerio — тенденция небольших смачиваемых плавающих объектов притягиваться друг к другу.
• Сплоченность
• Безразмерные числа
  • Номер облигации или номер Этвёша
  • Капиллярное число
  • Число Марангони
  • число Вебера
• Банк данных Дортмунда - содержит экспериментальные данные о поверхностном натяжении, зависящие от температуры.
• Электропогружающая сила
• Электросмачивание
• Электрокапиллярность
• Правило Этвеша — правило прогнозирования поверхностного натяжения в зависимости от температуры.
• Жидкостная труба
• Гидростатическое равновесие — эффект гравитации, притягивающий материю к круглой форме.
• Интерфейс (химия)
• Мениск — кривизна поверхности, образованная жидкостью в контейнере.
• Ртутное бьющееся сердце — следствие неоднородного поверхностного натяжения
• Микрофлюидика
• Техника сидячего падения
• Соу-Синь Чен
• Удельная поверхностная энергия — такая же, как поверхностное натяжение в изотропных материалах.
• Метод вращающейся капли
• Сталагмометрический метод
• Давление на поверхность
• Наука о поверхности
• Биомиметика поверхностного натяжения
• Значения поверхностного натяжения
• ПАВ — вещества, снижающие поверхностное натяжение.
• Уравнение Шишковского — расчет поверхностного натяжения водных растворов.
• Слезы вина — явление, вызванное поверхностным натяжением, наблюдаемое на стенках стаканов с алкогольными напитками.
• Длина Толмена — основной термин для коррекции поверхностного натяжения криволинейных поверхностей.
• Смачивание и обезвоживание

Внешние ссылки

• «Почему поверхностное натяжение параллельно границе раздела?» . Обмен стеками по физике . Проверено 19 марта 2021 г.
• Берри, М.В. (1 марта 1971 г.). «Молекулярный механизм поверхностного натяжения». Физическое образование . 6 (2): 79–84. дои : 10.1088/0031-9120/6/2/001. ISSN 0031-9120.
• Маршан, Антонен; Вейс, Йост Х.; Снойер, Жакко Х.; Андреотти, Бруно (26 сентября 2011 г.). «Почему поверхностное натяжение является силой, параллельной границе раздела?». Американский журнал физики . 79 (10): 999–1008. дои : 10.1119/1.3619866. ISSN 0002-9505. arXiv: https://arxiv.org/abs/1211.3854
• О поверхностном натяжении и интересных случаях из реальной жизни
• Поверхностное натяжение различных жидкостей
• Расчет зависимого от температуры поверхностного натяжения для некоторых распространенных компонентов.
• Калькулятор поверхностного натяжения водных растворов, содержащих ионы H ⁺ , Нью-Хэмпшир ⁺
  ₄ , Это ⁺ , К ⁺ , мг ²⁺ , Как ²⁺ , ТАК ²⁻
  ₄ , НЕТ ⁻
  ₃ , кл. ⁻ , Колорадо ²⁻
  ₃ , Бр. ⁻ и ох ⁻ .
• Т. Проктор Холл (1893) Новые методы измерения поверхностного натяжения в жидкостях , Философский журнал (серия 5, 36: 385–415), ссылка из Библиотеки наследия биоразнообразия .
• Пузырьковая стена (Аудиослайд-шоу из Национальной лаборатории сильных магнитных полей, объясняющее когезию, поверхностное натяжение и водородные связи)
• К. Пфистер: Свободная энергия интерфейса. Scholarpedia 2010 (из первых принципов статистической механики)
• Поверхностное и межфазное натяжение
• «Поверхностное натяжение смеси расплавленных солей». Журнал химической термодинамики . 3 (2): 259–265. Март 1971 г. doi : 10.1016/S0021-9614(71)80111-8 .