Напряжение (физика)

Натяжение — это тянущая или растягивающая сила, передаваемая в осевом направлении вдоль объекта, такого как веревка, веревка, цепь, стержень, элемент фермы или другой объект, с целью растягивания или разрыва объекта. С точки зрения силы это противоположно сжатию . Напряжение также можно описать как пару сил действие-противодействие, действующих на каждом конце объекта.

На атомном уровне, когда атомы или молекулы отрываются друг от друга и получают потенциальную энергию при сохраняющейся восстанавливающей силе , восстанавливающая сила может создать то, что также называется напряжением. Каждый конец веревки или стержня под таким натяжением может натянуть объект, к которому он прикреплен, чтобы восстановить расслабленную длину веревки/стержня.

Напряжение (как передаваемая сила, как пара сил действие-противодействие или как восстанавливающая сила) измеряется в ньютонах в Международной системе единиц (или фунтах-силах в имперских единицах ). Концы веревки или другого объекта, передающего натяжение, будут оказывать воздействие на объекты, к которым присоединена веревка или стержень, в направлении веревки в точке крепления. Эти силы, возникающие вследствие напряжения, также называются «пассивными силами». Есть две основные возможности для систем объектов, удерживаемых строками: ^[1] либо ускорение равно нулю и, следовательно, система находится в равновесии, либо есть ускорение, и, следовательно, результирующая сила в системе присутствует .

Напряжение в одном измерении

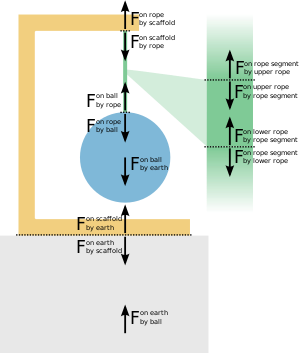
Натяжение в струне — неотрицательная векторная величина . Нулевое напряжение является слабым. Струна или веревка часто идеализируются как одномерные, имеющие длину, но невесомые и с нулевым поперечным сечением . Если в струне нет изгибов, как это происходит при вибрации или блоках , то натяжение вдоль струны является постоянным, равным величине сил, приложенных концами струны. Согласно третьему закону Ньютона , это те же силы, которые действуют на концы струны со стороны объектов, к которым эти концы прикреплены. Если струна огибает один или несколько блоков, она все равно будет иметь постоянное натяжение по всей длине в идеализированной ситуации, когда блоки не имеют массы и трения . колеблется Вибрирующая струна с набором частот , которые зависят от натяжения струны. Эти частоты можно вывести из законов движения Ньютона . Каждый микроскопический сегмент струны тянется и притягивается соседними сегментами с силой, равной натяжению в этом положении струны.

Если струна имеет кривизну, то два натяжения сегмента со стороны двух его соседей не будут суммироваться с нулем, и будет действовать результирующая сила на этот сегмент струны , вызывающая ускорение. Эта результирующая сила является восстанавливающей силой , и движение струны может включать поперечные волны , которые решают центральное уравнение теории Штурма – Лиувилля : $-{\frac {\mathrm {d} }{\mathrm {d} x}}{\bigg [}\tau (x){\frac {\mathrm {d} \rho (x)}{\mathrm {d} x}}{\bigg ]}+v(x)\rho (x)=\omega ^{2}\sigma (x)\rho (x)$ где $v(x)$ - силовая постоянная на единицу длины [единицы силы на площадь], $\sigma (x)$ это ...., $\tau (x)$ это ...., и $\omega ^{2}$ – собственные значения резонансов поперечного смещения $\rho (x)$ на веревке, ^[2] с решениями, включающими различные гармоники струнного инструмента .

Напряжение трех измерений

Натяжение также используется для описания силы, действующей на концы трехмерного непрерывного материала, такого как стержень или ферменный элемент. В этом контексте напряжение аналогично отрицательному давлению . Стержень под напряжением удлиняется . Величина удлинения и нагрузка , которая приведет к разрушению, зависят от силы, приходящейся на площадь поперечного сечения, а не только от силы, поэтому напряжение = осевая сила / площадь поперечного сечения более полезно для инженерных целей, чем растяжение. Напряжение представляет собой матрицу 3x3, называемую тензором , а $\sigma _{11}$ Элементом тензора напряжений является растягивающая сила на площадь или сила сжатия на площадь, обозначаемая как отрицательное число для этого элемента, если стержень сжимается, а не удлиняется.

Таким образом, можно получить скаляр, аналогичный натяжению, взяв след тензора напряжений. ^[3]

Система в равновесии

Система находится в равновесии, когда сумма всех сил равна нулю. ^[1] $\sum {\vec {F}}=0$

Например, рассмотрим систему, состоящую из объекта, который опускается вертикально с помощью веревки с натяжением T с постоянной скоростью . Система имеет постоянную скорость и, следовательно, находится в равновесии, поскольку натяжение струны, натягивающей объект, равно веса силе мг («м» — масса, «г» — ускорение, вызываемое гравитация Земли ), которая тянет объект вниз. ^[1] $\sum {\vec {F}}={\vec {T}}+m{\vec {g}}=0$

Система под чистой силой

Система имеет чистую силу, когда на нее действует несбалансированная сила, другими словами, сумма всех сил не равна нулю. Ускорение и чистая сила всегда существуют вместе. ^[1] $\sum {\vec {F}}\neq 0$

Например, рассмотрим ту же систему, что и выше, но предположим, что объект теперь опускается вниз с возрастающей скоростью (положительное ускорение), поэтому где-то в системе существует результирующая сила. В этом случае отрицательное ускорение будет означать, что $|mg|>|T|$ . ^[1] $\sum {\vec {F}}={\vec {T}}-m{\vec {g}}\neq 0$

В другом примере предположим, что два тела A и B, имеющие массы $m_{1}$ и $m_{2}$ , соответственно, соединены друг с другом нерастяжимой нитью через бесфрикционный шкив. На тело А действуют две силы: его вес ( $w_{1}=m_{1}g$ ) тянет вниз, и напряжение $T$ в тянущейся верёвке. Следовательно, чистая сила $F_{1}$ на теле А есть $w_{1}-T$ , так $m_{1}a=m_{1}g-T$ . В растяжимой струне закон Гука действует .

Струны в современной физике

Струноподобные объекты в релятивистских теориях, такие как струны, используемые в некоторых моделях взаимодействия между кварками , или те, которые используются в современной теории струн , также обладают напряжением. Эти строки анализируются с точки зрения их мирового листа , и тогда энергия обычно пропорциональна длине строки. В результате натяжение таких струн не зависит от степени растяжения.

См. также

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и Физика для ученых и инженеров с современной физикой , раздел 5.7. Седьмое издание, Brooks/Cole Cengage Learning, 2008.
^ А. Феттер и Дж. Валецка. (1980). Теоретическая механика частиц и сплошных сред . Нью-Йорк: МакГроу-Хилл.
^ Джаячандран, Арул. Проектирование напряженных элементов: механические свойства и разрушение блока при сдвиге, упражнения по гражданскому строительству, 9 апреля 2014 г., Технологический институт Иллинойса.

[Physics-1] Перейти обратно: ^а ^б ^с ^д ^и Физика для ученых и инженеров с современной физикой , раздел 5.7. Седьмое издание, Brooks/Cole Cengage Learning, 2008.

[2] А. Феттер и Дж. Валецка. (1980). Теоретическая механика частиц и сплошных сред . Нью-Йорк: МакГроу-Хилл.

[3] Джаячандран, Арул. Проектирование напряженных элементов: механические свойства и разрушение блока при сдвиге, упражнения по гражданскому строительству, 9 апреля 2014 г., Технологический институт Иллинойса.

[1]

[2]

[3]