Специальная теория относительности

| Специальная теория относительности |
|---|
 |
В физике специальная теория относительности , или сокращенно специальная теория относительности , представляет собой научную теорию взаимосвязи между пространством и временем . В трактовке Альберта Эйнштейна 1905 года теория представлена как основанная всего на двух постулатах : [стр 1] [1] [2]
- Законы физики инвариантны ( идентичны ) во всех инерциальных системах отсчета (то есть системах отсчета без ускорения ).
- Скорость света в вакууме одинакова для всех наблюдателей, независимо от движения источника света или наблюдателя.
Первый постулат впервые был сформулирован Галилео Галилеем (см. Инвариантность Галилея ).
и значение Происхождение
Специальная теория относительности была описана Альбертом Эйнштейном в статье « К электродинамике движущихся тел », опубликованной 26 сентября 1905 года. [стр 1] оказались Максвелла Уравнения электромагнетизма несовместимыми с ньютоновской механикой , а эксперимент Майкельсона-Морли не смог обнаружить движение Земли против гипотетического светоносного эфира . Это привело к разработке преобразований Лоренца , которые корректируют расстояния и время для движущихся объектов. Специальная теория относительности корректирует существовавшие до сих пор законы механики, чтобы обрабатывать ситуации, включающие все движения, особенно те, которые происходят со скоростью, близкой к скорости света (известные как релятивистские скорости ). Сегодня доказано, что специальная теория относительности является наиболее точной моделью движения на любой скорости, когда гравитационные и квантовые эффекты незначительны. [3] [4] Несмотря на это, ньютоновская модель по-прежнему актуальна как простое и точное приближение при низких скоростях (относительно скорости света), например, при повседневных движениях на Земле.
Специальная теория относительности имеет широкий спектр следствий, подтвержденных экспериментально. [5] К ним относятся относительность одновременности , сокращение длины , замедление времени , релятивистская формула сложения скоростей, релятивистский эффект Доплера , релятивистская масса , универсальный предел скорости , эквивалентность массы и энергии , скорость причинности и прецессия Томаса . [1] [2] Например, оно заменило традиционное понятие абсолютного всемирного времени понятием времени, которое зависит от системы отсчета и пространственного положения. Вместо инвариантного временного интервала между двумя событиями существует инвариантный пространственно-временной интервал . В сочетании с другими законами физики два постулата специальной теории относительности предсказывают эквивалентность массы и энергии , как это выражено в эквивалентности массы и энергии. формуле , где это скорость света в вакууме. [6] [7] Это также объясняет, как связаны явления электричества и магнетизма. [1] [2]
Определяющей чертой специальной теории относительности является замена преобразований Галилея механики Ньютона преобразованиями Лоренца . Время и пространство не могут быть определены отдельно друг от друга (как считалось ранее). Скорее, пространство и время переплетаются в единый континуум, известный как «пространство-время» . События, происходящие одновременно для одного наблюдателя, могут происходить в разное время для другого.
До тех пор, пока несколько лет спустя Эйнштейн не разработал общую теорию относительности , которая ввела искривленное пространство-время для включения гравитации, фраза «специальная теория относительности» не использовалась. Иногда используется перевод «ограниченная теория относительности»; «Особый» на самом деле означает «особый случай». [стр. 2] [стр. 3] [стр. 4] [примечание 1] Некоторые работы Альберта Эйнштейна по специальной теории относительности основаны на более ранних работах Хендрика Лоренца и Анри Пуанкаре . Теория стала практически завершенной в 1907 году, когда появились Германа Минковского о пространстве-времени. статьи [4]
Теория является «особой» в том смысле, что она применима только в частном случае , когда пространство-время «плоское», то есть когда кривизна пространства-времени (следствие тензора энергии-импульса и представление гравитации ) незначительна. [8] [примечание 2] Чтобы правильно учесть гравитацию, Эйнштейн в 1915 году сформулировал общую теорию относительности. Специальная теория относительности, вопреки некоторым историческим описаниям, действительно учитывает как ускорения, так и ускоряющиеся системы отсчета . [9] [10]
Точно так же, как теория относительности Галилея сейчас считается приближением специальной теории относительности, справедливой для малых скоростей, специальная теория относительности считается приближением общей теории относительности, справедливой для слабых гравитационных полей , то есть в достаточно малом масштабе (например, когда приливные силы незначительны) и в условиях свободного падения . Но общая теория относительности включает неевклидову геометрию , чтобы представить гравитационные эффекты как геометрическую кривизну пространства-времени. Специальная теория относительности ограничена плоским пространством-временем, известным как пространство Минковского . Пока Вселенную можно смоделировать как псевдориманово многообразие , лоренц-инвариантную систему отсчета, которая подчиняется специальной теории относительности, можно определить для достаточно малой окрестности каждой точки в этом искривленном пространстве-времени .
Галилео Галилей уже постулировал, что не существует абсолютного и четко определенного состояния покоя (нет привилегированных систем отсчета ), принцип, который теперь называется принципом относительности Галилея . Эйнштейн расширил этот принцип так, что он объяснил постоянную скорость света. [11] явление, которое наблюдалось в эксперименте Майкельсона-Морли. Он также постулировал, что это справедливо для всех законов физики , включая законы механики и электродинамики . [12]
«двух постулатов Традиционный подход к специальной теории относительности »
«Размышления такого типа дали мне понять уже вскоре после 1900 года, т. е. вскоре после новаторской работы Планка, что ни механика, ни электродинамика не могут (за исключением предельных случаев) претендовать на точную достоверность. Постепенно я отчаялся в возможности открытия истинные законы посредством конструктивных усилий, основанных на известных фактах, чем дольше и отчаяннее я пытался, тем больше я приходил к убеждению, что только открытие универсального формального принципа может привести нас к гарантированным результатам... Как же тогда? , можно ли найти такой универсальный принцип?»
Альберт Эйнштейн: Автобиографические заметки [стр. 5]
Эйнштейн выделил два фундаментальных положения, которые казались наиболее достоверными, независимо от точной справедливости известных (тогда) законов механики или электродинамики. Этими положениями были постоянство скорости света в вакууме и независимость физических законов (особенно постоянства скорости света) от выбора инерциальной системы. В своей первой презентации специальной теории относительности в 1905 году он выразил эти постулаты следующим образом: [стр 1]
- Принцип относительности – на законы, по которым изменяются состояния физических систем, не влияет, относятся ли эти изменения состояния к той или иной из двух систем, находящихся в равномерном поступательном движении относительно друг друга. [стр 1]
- Принцип инвариантности скорости света – «...свет всегда распространяется в пустом пространстве с определенной скоростью [скоростью] c , которая не зависит от состояния движения излучающего тела» (из предисловия). [стр 1] То есть свет в вакууме распространяется со скоростью c (фиксированной постоянной, не зависящей от направления) по крайней мере в одной системе инерциальных координат («стационарной системе»), независимо от состояния движения источника света.
Постоянство скорости света было мотивировано теорией электромагнетизма Максвелла. [13] и отсутствие доказательств существования светоносного эфира . [14] Существуют противоречивые данные о том, в какой степени на Эйнштейна повлиял нулевой результат эксперимента Майкельсона-Морли. [15] [16] В любом случае нулевой результат эксперимента Майкельсона-Морли помог идее постоянства скорости света получить широкое и быстрое признание.
Вывод специальной теории относительности зависит не только от этих двух явных постулатов, но и от нескольких неявных предположений ( сделанных почти во всех теориях физики ), включая изотропность и однородность пространства и независимость измерительных стержней и часов от их прошлой истории. [стр. 6]
После первоначального представления специальной теории относительности Эйнштейном в 1905 году было предложено множество различных наборов постулатов в различных альтернативных вариантах. [17] Но наиболее распространенным набором постулатов остаются те, которые использовал Эйнштейн в своей оригинальной статье. Более математическое изложение принципа относительности, сделанное позднее Эйнштейном и вводящее не упомянутую выше концепцию простоты, звучит так:
Специальный принцип относительности : если система координат K выбрана так, что по отношению к ней действуют физические законы в своей простейшей форме, то те же законы справедливы и по отношению к любой другой системе координат K ', движущейся равномерно поступательно относительно к К. [18]
Анри Пуанкаре обеспечил математическую основу теории относительности, доказав, что преобразования Лоренца являются подмножеством его Пуанкаре группы преобразований симметрии . Позже Эйнштейн вывел эти преобразования из своих аксиом.
Во многих статьях Эйнштейна представлены выводы преобразования Лоренца, основанные на этих двух принципах. [стр. 7]
Принцип относительности [ править ]
Системы отсчета движение относительное и

Системы отсчета играют решающую роль в теории относительности. Используемый здесь термин «система отсчета» представляет собой перспективу наблюдения в пространстве, не претерпевающую никаких изменений в движении (ускорении), из которой можно измерить положение вдоль трех пространственных осей (то есть в состоянии покоя или с постоянной скоростью). Кроме того, система отсчета имеет возможность определять измерения времени событий с помощью «часов» (любого отсчетного устройства с равномерной периодичностью).
Событие — это событие , которому можно присвоить единственный уникальный момент и местоположение в пространстве относительно системы отсчета: это «точка» в пространстве-времени . Поскольку скорость света постоянна в теории относительности независимо от системы отсчета, импульсы света можно использовать для однозначного измерения расстояний и отсчета времени, когда события произошли с часами, даже если свету требуется время, чтобы достичь часов после события. произошло.
Например, взрыв петарды можно считать «событием». Мы можем полностью определить событие по его четырем пространственно-временным координатам: время возникновения и его трехмерное пространственное положение определяют точку отсчета. Назовем эту систему S. отсчета
В теории относительности мы часто хотим вычислить координаты события из разных систем отсчета. Уравнения, связывающие измерения, выполненные в разных системах отсчета, называются уравнениями преобразования .
Стандартная конфигурация [ править ]
Чтобы получить представление о том, как координаты пространства-времени, измеренные наблюдателями в разных системах отсчета, соотносятся друг с другом, полезно работать с упрощенной установкой с системами стандартной конфигурации. [19] : 107 При осторожном подходе это позволяет упростить математические расчеты без потери общности полученных выводов. На рис. 2-1 две системы отсчета Галилея (т.е. обычные трехмерные системы координат) показаны в относительном движении. Кадр S принадлежит первому наблюдателю O, а кадр S ′ (произносится как «S prime» или «S тире») принадлежит второму наблюдателю O ′ .
- Оси x , y , z кадра S ориентированы параллельно соответствующим осям со штрихом кадра S ' .
- Для простоты кадр S ' движется в одном направлении: в направлении x кадра S с постоянной скоростью v , измеренной в кадре S.
- Начало кадров S и S ′ совпадает, когда время t = 0 для кадра S и t ′ = 0 для кадра S ′ .
Поскольку в теории относительности не существует абсолютной системы отсчета, понятия «движение» строго не существует, поскольку все может двигаться относительно какой-то другой системы отсчета. Вместо этого говорят, что любые два кадра, которые движутся с одинаковой скоростью в одном направлении, движутся навстречу друг другу . Следовательно, S и S ’ не движутся вместе .
Отсутствие абсолютной системы отсчета [ править ]
Принцип относительности , который утверждает, что физические законы имеют одинаковую форму в каждой инерциальной системе отсчета , восходит к Галилею и был включен в ньютоновскую физику. Но в конце 19-го века существование электромагнитных волн побудило некоторых физиков предположить, что Вселенная заполнена веществом, которое они назвали « эфиром », которое, как они постулировали, должно действовать как среда, через которую распространяются эти волны или вибрации ( во многом аналогично тому, как звук распространяется в воздухе). Считалось, что эфир является абсолютной системой отсчета , относительно которой можно было измерить все скорости, и его можно было считать фиксированным и неподвижным относительно Земли или какой-либо другой фиксированной точки отсчета. Эфир должен был быть достаточно эластичным, чтобы поддерживать электромагнитные волны, в то время как эти волны могли взаимодействовать с материей, не оказывая при этом сопротивления проходящим через него телам (его единственным свойством было то, что он позволял распространяться электромагнитным волнам). Результаты различных экспериментов, в том числе эксперимента Майкельсона-Морли в 1887 году (впоследствии подтвержденного более точными и новаторскими экспериментами), привели к созданию специальной теории относительности, показав, что эфира не существует. [20] Решением Эйнштейна было отказаться от понятия эфира и абсолютного состояния покоя. В теории относительности любая система отсчета, движущаяся равномерно, подчиняется одним и тем же законам физики. В частности, скорость света в вакууме всегда измеряется как c , даже если ее измеряют несколько систем, движущихся с разными (но постоянными) скоростями.
Относительность без второго постулата [ править ]
Только на основе принципа относительности, не предполагая постоянства скорости света (т. е. используя изотропию пространства и симметрию, подразумеваемую принципом специальной теории относительности), можно показать , что преобразования пространства-времени между инерциальными системами отсчета являются либо евклидовыми, либо галилеевскими. , или лоренциан. В лоренцевом случае тогда можно получить сохранение релятивистского интервала и некоторую конечную предельную скорость. Эксперименты показывают, что эта скорость равна скорости света в вакууме. [стр. 8] [21]
Лоренц-инвариантность как основное ядро относительности теории специальной
подходы к специальной относительности теории Альтернативные
Эйнштейн последовательно основывал вывод лоренц-инвариантности (основного ядра специальной теории относительности) только на двух основных принципах теории относительности и инвариантности скорости света. Он написал:
Фундаментальное для специальной теории относительности положение таково: предположения относительности и инвариантности скорости света совместимы, если постулируются соотношения нового типа («преобразование Лоренца») для преобразования координат и времен событий... Универсальный принцип Специальной теории относительности содержится в постулате: Законы физики инвариантны относительно преобразований Лоренца (при переходе от одной инерциальной системы к любой другой, произвольно выбранной инерциальной системе). Это ограничивающий принцип для естественных законов... [стр. 5]
Таким образом, многие современные трактовки специальной теории относительности основывают ее на единственном постулате универсальной ковариантности Лоренца или, что то же самое, на единственном постулате пространства-времени Минковского . [стр. 9] [стр. 10]
Вместо того, чтобы рассматривать универсальную ковариацию Лоренца как производный принцип, в этой статье она рассматривается как фундаментальный постулат специальной теории относительности. Традиционный подход к специальной теории относительности, основанный на двух постулатах, представлен в бесчисленных учебниках для колледжей и популярных презентациях. [22] Учебники, начинающиеся с единственного постулата пространства-времени Минковского, включают учебники Тейлора и Уиллера. [23] и Каллахан. [24] Этому же подходу следуют статьи Википедии «Пространство-время» и «Диаграмма Минковского» .
Преобразование Лоренца и обратное ему [ править ]
Определите событие , чтобы оно имело пространственно-временные координаты ( t , x , y , z ) в системе S и ( t ' , x ' , y ' , z ' ) в системе отсчета, движущейся со скоростью v по оси x относительно этого события. кадр, S ′ . Тогда преобразование Лоренца указывает, что эти координаты связаны следующим образом:
Решение четырех приведенных выше уравнений преобразования для координат без штриха дает обратное преобразование Лоренца:
Это показывает, что кадр без штриха движется со скоростью - v , измеренной в кадре со штрихом. [25]
нет ничего особенного В оси X . Преобразование может применяться к осям y или z , или даже в любом направлении, параллельном движению (которое искривляется фактором γ ) и перпендикулярно; см. в статье «Преобразование Лоренца» Подробности .
Величина, инвариантная относительно преобразований Лоренца , известна как скаляр Лоренца .
Записывая преобразование Лоренца и обратное ему через разность координат, где одно событие имеет координаты ( x 1 , t 1 ) и ( x ′ 1 , t ′ 1 ) , другое событие имеет координаты ( x 2 , t 2 ) и ( x ′ 2 , t ′ 2 ) , а разности определяются как
- уравнение 1:
- уравнение 2:
мы получаем
- уравнение 3:
- уравнение 4:
Если вместо разностей мы возьмем дифференциалы, мы получим
- уравнение 5:
- уравнение 6:
преобразования Графическое представление Лоренца
Диаграммы пространства-времени ( диаграммы Минковского ) являются чрезвычайно полезным средством визуализации того, как преобразуются координаты между различными системами отсчета. Хотя выполнить точные вычисления с их помощью не так просто, как с помощью преобразований Лоренца напрямую, их главная сила заключается в способности обеспечивать интуитивное понимание результатов релятивистского сценария. [21]
Чтобы нарисовать диаграмму пространства-времени, начните с рассмотрения двух систем отсчета Галилея, S и S', в стандартной конфигурации, как показано на рис. 2-1. [21] [26] : 155–199
Рис. 3-1а. Нарисуйте и оси рамки S. ось горизонтальна, а (на самом деле ) ось вертикальна, что противоречит обычному соглашению в кинематике. ось масштабируется с коэффициентом так что обе оси имеют общие единицы длины. На показанной диаграмме линии сетки расположены на расстоянии одной единицы друг от друга. Диагональные линии под углом 45° представляют собой мировые линии двух фотонов, проходящих через начало координат в определенный момент времени. Наклон этих мировых линий равен 1, поскольку фотоны перемещаются в пространстве на одну единицу за единицу времени. Два события, и были нанесены на этот график, чтобы их координаты можно было сравнить в кадрах S и S'.
Рис. 3-1б. Нарисуйте и оси системы S'. Ось представляет мировую линию начала системы координат S, измеренную в системе отсчета S. На этом рисунке Оба и оси наклонены от незаштрихованных осей на угол где Оси со штрихом и без штриха имеют общее начало, поскольку кадры S и S' были настроены в стандартной конфигурации, так что когда
Рис. 3-1в. Единицы измерения на заштрихованных осях имеют другой масштаб, чем единицы измерения на незаштрихованных осях. Из преобразований Лоренца мы видим, что координаты в штрихованной системе координат преобразуются в в незаштрихованной системе координат. Так же, координаты в штрихованной системе координат преобразуются в в неосновной системе. Рисовать линии сетки параллельно ось через точки как измерено в незаштрихованной рамке, где является целым числом. Аналогичным образом нарисуйте линии сетки параллельно ось через как измерено в незаштрихованной рамке. Используя теорему Пифагора, мы наблюдаем, что расстояние между единицы равны раз больше расстояния между единиц, измеренных в системе отсчета S. Это соотношение всегда больше 1 и в конечном итоге приближается к бесконечности, поскольку
Рис. 3-1г. Поскольку скорость света является инвариантом, мировые линии двух фотонов, проходящих через начало координат в момент времени по-прежнему изображайте диагональные линии под углом 45 °. Заштрихованные координаты и связаны с координатами без штриха посредством преобразований Лоренца и могут быть приблизительно измерены по графику (при условии, что он построен достаточно точно), но настоящее достоинство диаграммы Минковского заключается в том, что она дает нам геометрическое представление о сценарии. Например, на этом рисунке мы видим, что два разделенных во времени события, которые имели разные координаты x в незаштрихованном кадре, теперь находятся в одном и том же положении в пространстве.
В то время как незаштрихованный кадр рисуется с осями пространства и времени, пересекающимися под прямыми углами, заштрихованный кадр рисуется с осями, которые пересекаются под острыми или тупыми углами. Эта асимметрия возникает из-за неизбежных искажений в том, как координаты пространства-времени отображаются на декартовой плоскости , но на самом деле системы отсчета эквивалентны.
из преобразования Лоренца Последствия , вытекающие
Следствия специальной теории относительности можно вывести из уравнений преобразования Лоренца . [27] Эти преобразования, а, следовательно, и специальная теория относительности, приводят к иным физическим предсказаниям, чем предсказания ньютоновской механики при всех относительных скоростях, и наиболее ярко выражены, когда относительные скорости становятся сравнимыми со скоростью света. Скорость света настолько превышает скорость света, с которой сталкивается большинство людей, что некоторые из эффектов, предсказанных теорией относительности, поначалу противоречат здравому смыслу .
Инвариантный интервал [ править ]
В теории относительности Галилея длина объекта ( ) [примечание 3] и временное разделение между двумя событиями ( ) являются независимыми инвариантами, значения которых не изменяются при наблюдении из разных систем отсчета. [примечание 4] [примечание 5]
Однако в специальной теории относительности переплетение пространственных и временных координат порождает концепцию инвариантного интервала , обозначаемого как : [примечание 6]
Переплетение пространства и времени отменяет неявно принятые концепции абсолютной одновременности и синхронизации между несмежными кадрами.
Форма будучи разницей квадрата промежутка времени и квадрата пространственного расстояния, демонстрирует фундаментальное несоответствие между евклидовым и пространственно-временным расстояниями. [примечание 7] Инвариантность этого интервала является свойством общего преобразования Лоренца (также называемого преобразованием Пуанкаре ), что делает его изометрией пространства-времени. Общее преобразование Лоренца расширяет стандартное преобразование Лоренца (которое имеет дело с перемещениями без вращения, то есть усилением Лоренца в направлении x) всеми другими перемещениями , отражениями и вращениями между любой декартовой инерциальной системой отсчета. [31] : 33–34
При анализе упрощенных сценариев, таких как пространственно-временные диаграммы, часто используется форма инвариантного интервала с уменьшенной размерностью:
Продемонстрировать, что интервал инвариантен, несложно для случая пониженной размерности и с кадрами в стандартной конфигурации: [21]
Стоимость следовательно, не зависит от системы отсчета, в которой он измеряется.
Учитывая физическое значение , следует отметить три случая: [21] [32] : 25–39
- Δс 2 > 0: В этом случае два события разделены большим временем, чем пространством, и, следовательно, о них говорят, что они разделены во времениподобно . Это означает, что и учитывая преобразование Лоренца очевидно, что существует меньше, чем для чего (в частности, ). Другими словами, учитывая два события, которые разделены во времени, можно найти кадр, в котором эти два события происходят в одном и том же месте. В этом кадре разделение во времени, называется собственным временем .
- Δс 2 < 0: в этом случае два события разделены большим пространством, чем временем, и поэтому говорят, что они разделены пространственно-подобно . Это означает, что и учитывая преобразование Лоренца существует меньше, чем для чего (в частности, ). Другими словами, учитывая два события, разделенных пространством, можно найти кадр, в котором эти два события происходят одновременно. В этом кадре разлука в пространстве, называется правильным расстоянием или правильной длиной . Для значений больше и меньше чем знак меняется, то есть временной порядок пространственно-подобных событий меняется в зависимости от кадра, в котором события рассматриваются. Но временной порядок событий, разделенных во времениподобным образом, абсолютен, поскольку единственный способ может быть больше, чем было бы, если бы
- Δс 2 = 0: в этом случае говорят, что два события разделены светоподобно . Это означает, что и это соотношение не зависит от системы координат из-за инвариантности Отсюда мы видим, что скорость света равна в каждой инерциальной системе отсчета. Другими словами, исходя из предположения об универсальной ковариации Лоренца, постоянная скорость света является производным результатом, а не постулатом, как в формулировке специальной теории с двумя постулатами.
Относительность одновременности [ править ]

Рассмотрим два события, происходящие в двух разных местах одновременно в системе отсчета одного инерциального наблюдателя. Они могут возникнуть неодновременно в системе отсчета другого инерциального наблюдателя (отсутствие абсолютной одновременности ).
Из уравнения 3 (прямое преобразование Лоренца с точки зрения разности координат)
Ясно, что два события, которые одновременны в системе отсчета = 0 ) S (удовлетворяющие Δt , не обязательно одновременны в другой инерциальной системе отсчета ' ( удовлетворяющей Δt ' S = 0 ). Только если эти события дополнительно локальны в кадре S (удовлетворяющие Δx кадре = 0 ), они будут одновременными в другом S ' .
Эффект Саньяка можно считать проявлением относительности одновременности. [33] Поскольку относительность одновременности является эффектом первого порядка в , [21] инструменты, основанные на эффекте Саньяка для своей работы, такие как кольцевые лазерные гироскопы и волоконно-оптические гироскопы , способны достигать экстремальных уровней чувствительности. [стр. 14]
Замедление времени [ править ]
Промежуток времени между двумя событиями не инвариантен от одного наблюдателя к другому, но зависит от относительных скоростей систем отсчета наблюдателей.
Предположим, что покоятся в незаштрихованной системе S. часы Тогда положение часов на двух разных тактах характеризуется Δ x = 0 . Чтобы найти связь между временем между этими тактами, измеренным в обеих системах, уравнение 3, можно использовать чтобы найти:
- для мероприятий, удовлетворяющих
Это показывает, что время (Δt ' ) между двумя тактами, как видно в кадре, в котором движутся часы ( S ' ), больше , чем время (Δt ) между этими тактами, измеренное в остальном кадре часы ( С ). Замедление времени объясняет ряд физических явлений; например, время жизни высокоскоростных мюонов , созданных при столкновении космических лучей с частицами во внешней атмосфере Земли и движущихся к поверхности, больше, чем время жизни медленно движущихся мюонов, созданных и распадающихся в лаборатории. [34]

Всякий раз, когда кто-то слышит утверждение о том, что «движущиеся часы идут медленно», ему следует представить себе инерциальную систему отсчета, густо населенную идентичными синхронизированными часами. Когда движущиеся часы проходят через этот массив, их показания в любой конкретной точке сравниваются с показаниями неподвижных часов в той же точке. [35] : 149–152
Измерения, которые мы получили бы, если бы на самом деле посмотрели на движущиеся часы, в общем, были бы совсем не теми же самыми, потому что время, которое мы видели бы, задерживалось бы из-за конечной скорости света, т.е. искажаться эффектом Доплера . Измерения релятивистских эффектов всегда следует понимать как выполненные после исключения эффектов конечной скорости света. [35] : 149–152
Световые часы Ланжевена [ править ]

Поль Ланжевен , один из первых сторонников теории относительности, много сделал для популяризации теории, несмотря на сопротивление многих физиков революционным концепциям Эйнштейна. Среди его многочисленных вкладов в основы специальной теории относительности были независимая работа по взаимосвязи массы и энергии, тщательное исследование парадокса близнецов и исследования вращающихся систем координат. Его имя часто связывают с гипотетической конструкцией, называемой «световые часы» (первоначально разработанной Льюисом и Толманом в 1909 году). [36] ), который он использовал для нового вывода преобразования Лоренца. [37]
Световые часы представляют собой коробку с идеально отражающими стенами, в которой световой сигнал отражается взад и вперед от противоположных сторон. Концепция замедления времени часто преподается с использованием световых часов, которые движутся по равномерной инерции, перпендикулярно линии, соединяющей два зеркала. [38] [39] [40] [41] (Сам Ланжевен пользовался световыми часами, ориентированными параллельно линии их движения. [37] )
Рассмотрим сценарий, показанный на рис. 4-3А. Наблюдатель А держит световые часы длиной а также электронный таймер, с помощью которого она измеряет, сколько времени требуется пульсу, чтобы пройти туда и обратно по световым часам. Хотя наблюдатель А быстро движется по поезду, с его точки зрения испускание и получение импульса происходят в одном и том же месте, и он измеряет интервал с помощью единственных часов, расположенных точно в месте этих двух событий. Для интервала между этими двумя событиями наблюдатель А находит Интервал времени, измеряемый с помощью одних часов, неподвижных в определенной системе отсчета, называется собственным интервалом времени . [42]
Рис. 4-3B иллюстрирует эти же два события с точки зрения наблюдателя B, который припарковался у путей, когда поезд проезжает со скоростью Вместо того чтобы совершать прямые движения вверх и вниз, наблюдатель Б видит, как импульсы движутся по зигзагообразной линии. Однако из-за постулата постоянства скорости света скорость импульсов вдоль этих диагональных линий одинакова это наблюдатель А видел по ее пульсу вверх и вниз. B измеряет скорость вертикальной составляющей этих импульсов как так что общее время прохождения импульсов туда и обратно равно Обратите внимание, что для наблюдателя Б испускание и получение светового импульса происходило в разных местах, и он измерял интервал с помощью двух стационарных и синхронизированных часов, расположенных в двух разных положениях его системы отсчета. Таким образом, интервал, который измерял B, не был подходящим временным интервалом, поскольку он не измерял его с помощью одних покоящихся часов. [42]
Взаимное замедление времени [ править ]
В приведенном выше описании световых часов Ланжевена обозначение одного наблюдателя как неподвижного, а другого как движущегося было совершенно произвольным. С таким же успехом можно было бы представить наблюдателя Б, несущего световые часы и движущегося со скоростью влево, и в этом случае наблюдатель A будет воспринимать часы B как идущие медленнее, чем ее местные часы.
Здесь нет парадокса, потому что не существует независимого наблюдателя C, который был бы согласен и с A, и с B. Наблюдатель C обязательно производит свои измерения из своей собственной системы отсчета. Если эта система отсчета совпадает с системой отсчета A, то C будет соответствовать измерению времени A. Если система отсчета C совпадает с системой отсчета B, то C согласуется с измерением времени B. Если система отсчета C не совпадает ни с системой отсчета A, ни с системой B, то измерение времени C не будет расходиться с измерением времени как A, так и B. [43]
Парадокс близнецов [ править ]
Взаимное замедление времени между двумя наблюдателями в отдельных инерциальных системах отсчета приводит к так называемому парадоксу близнецов , сформулированному в его нынешней форме Ланжевеном в 1911 году. [44] Ланжевен представлял себе авантюриста, желающего исследовать будущее Земли. Этот путешественник садится на снаряд, способный двигаться со скоростью 99,995% скорости света. Совершив путешествие туда и обратно к ближайшей звезде и обратно, продолжавшееся всего два года его собственной жизни, он возвращается на Землю, которая на двести лет старше.
Этот результат кажется загадочным, поскольку и путешественник, и наблюдатель с Земли видели бы другого движущимся, и поэтому из-за взаимного замедления времени можно было бы первоначально ожидать, что каждый из них должен был обнаружить, что другой постарел меньше. В действительности никакого парадокса вообще нет, поскольку для того, чтобы два наблюдателя могли сравнить свои собственные времена, необходимо нарушить симметрию ситуации: по крайней мере один из двух наблюдателей должен изменить свое состояние движения так, чтобы оно соответствовало состоянию движения второго наблюдателя. другой. [45]

Однако знание общего разрешения парадокса не дает сразу возможности вычислить правильные количественные результаты. Многие решения этой загадки были предложены в литературе и рассмотрены в статье «Парадокс близнецов» . Ниже мы рассмотрим одно из таких решений парадокса.
Нашей основной целью будет продемонстрировать, что после поездки оба близнеца пришли к полному согласию относительно того, кто и насколько постарел, независимо от их разного опыта. Рис. 4-4 иллюстрирует сценарий, в котором путешествующий двойник летит на расстоянии 0,6 c к звезде и от нее, находящейся на расстоянии 3 лет . Во время путешествия каждый близнец посылает друг другу ежегодные сигналы времени (измеренные в их собственном времени). После поездки совокупные значения сравниваются. На исходной фазе путешествия каждый близнец получает сигналы другого с пониженной скоростью. Первоначально ситуация совершенно симметрична: обратите внимание, что каждый близнец получает годовой сигнал другого через два года, измеренные по их собственным часам. Симметрия нарушается, когда путешествующий близнец разворачивается на отметке четырех лет, измеренной ее часами. В течение оставшихся четырех лет своего путешествия она получает сигналы с повышенной скоростью. Совершенно иначе обстоит дело со стационарным двойником. Из-за задержки со скоростью света он не видит, как его сестра обернулась, пока по его собственным часам не пройдет восемь лет. Таким образом, он получает усиленные сигналы от своей сестры лишь в течение относительно короткого периода времени. Хотя близнецы расходятся в своих измерениях общего времени, мы видим из следующей таблицы, а также путем простого наблюдения диаграммы Минковского, что каждый близнец полностью согласуется с другим относительно общего количества сигналов, отправленных от одного близнеца. другому. Следовательно, никакого парадокса нет. [35] : 152–159
| Элемент | Измерено сидеть дома | Рис. 4-4 | Измерено путешественник | Рис. 4-4 |
|---|---|---|---|---|
| Общее время поездки | 10 лет | 8 лет | ||
| Общее количество отправленных импульсов | 10 | 8 | ||
| поворот путешественника Время, когда обнаружен | 8 лет | 4 | ||
| Количество импульсов, полученных в начале ставка | | 4 | | 2 |
| Время до конца поездки | 2 года | 4 | ||
| Количество сигналов, полученных в финале ставка | 4 | 8 | ||
| Общее количество полученных импульсов | 8 | 10 | ||
| Расчет близнеца относительно того, насколько другой должен был постареть близнец | 8 лет | 10 лет |
длины Сокращение
Размеры (например, длина) объекта, измеренные одним наблюдателем, могут быть меньше, чем результаты измерений того же объекта, сделанные другим наблюдателем (например, парадокс лестницы предполагает, что длинная лестница движется со скоростью, близкой к скорости света, и удерживается в небольшом гараже).
Аналогично предположим, что измерительный стержень покоится и выровнен вдоль оси x в незаштрихованной S. системе В этой системе длина этого стержня записывается как Δx . Для измерения длины этого стержня в системе S ' , в которой стержень движется, необходимо одновременно измерить расстояния x ' до концов стержня в этой системе S ' . Другими словами, измерение характеризуется Δ t ′ = 0 , что можно объединить с уравнением 4, чтобы найти связь между длинами Δ x и Δ x ′ :
- для мероприятий, удовлетворяющих
Это показывает, что длина (Δ x ′ ) стержня, измеренная в системе отсчета, в которой он движется ( S ′ ), короче , чем его длина (Δ x ) в собственной системе отсчета покоя ( S ).
Замедление времени и сокращение длины — это не просто видимость. Замедление времени явно связано с нашим способом измерения временных интервалов между событиями, которые происходят в одном и том же месте в данной системе координат (так называемые «совместные» события). Эти временные интервалы (которые могут быть измерены и фактически измеряются соответствующими наблюдателями экспериментально) различны в другой системе координат, движущейся относительно первой, если только события, помимо того, что они солокальны, еще и одновременны. Аналогичным образом, сокращение длины связано с измеренными нами расстояниями между отдельными, но одновременными событиями в выбранной системе координат. Если эти события не локальны, а разделены расстоянием (пространством), они не будут происходить на одинаковом пространственном расстоянии друг от друга, если смотреть из другой движущейся системы координат.
Лоренцево преобразование скоростей [ править ]
Рассмотрим два кадра S и S ′ в стандартной конфигурации. Частица в S движется в направлении x с вектором скорости Какова его скорость в кадре S ' ?
Мы можем написать
| ( 7 ) |
| ( 8 ) |
Замена выражений на и из уравнения 5 в уравнение 8 , после чего следуют простые математические манипуляции и обратная замена из уравнения 7, что дает преобразование Лоренца скорости к :
| ( 9 ) |
Обратная связь получается путем замены штрихованных и нештрихованных символов местами и замены с
| ( 10 ) |
Для не выровнены по оси x, запишем: [12] : 47–49
| ( 11 ) |
| ( 12 ) |
Прямые и обратные преобразования для этого случая:
| ( 13 ) |
| ( 14 ) |
Уравнение 10 и уравнение 14 можно интерпретировать как дающие результирующую из двух скоростей и и они заменяют формулу что справедливо в теории относительности Галилея. Интерпретированные таким образом, их обычно называют формулами релятивистского сложения (или композиции) скоростей , действительными для трех осей S и S ', выровненных друг с другом (хотя и не обязательно в стандартной конфигурации). [12] : 47–49
Отмечаем следующие моменты:
- Если бы объект (например, фотон ) двигался со скоростью света в одном кадре (т. е. u = ± c или u ′ = ± c ), то он также двигался бы со скоростью света в любом другом кадре, переезд | в | < с .
- Результирующая скорость двух скоростей с величиной меньше c всегда будет скоростью с величиной меньше c .
- Если оба | ты | и | в | (а тогда еще | u ′ | и | v ′ |) малы по отношению к скорости света (т.е., например, | у / ц | ≪ 1 ), то интуитивные преобразования Галилея восстанавливаются из уравнений преобразования специальной теории относительности
- Прикрепление рамки к фотону ( движение светового луча, как считает Эйнштейн) требует особого подхода к преобразованиям.
нет ничего особенного x В стандартной конфигурации в направлении . Приведенный выше формализм применим к любому направлению; а три ортогональных направления позволяют иметь дело со всеми направлениями в пространстве, разлагая векторы скорости на их компоненты в этих направлениях. см. в формуле сложения скорости Подробности .
Ротация Томаса [ править ]
Композиция двух неколлинеарных преобразований Лоренца (т.е. двух неколлинеарных преобразований Лоренца, ни одно из которых не включает вращение) приводит к преобразованию Лоренца, которое не является чистым повышением, а представляет собой композицию повышения и вращения.
Вращение Томаса является результатом относительности одновременности. На рис. 4-5а стержень длиной в своей системе покоя (т. е. имея правильную длину ) поднимается вертикально вдоль оси Y в наземном кадре.
На рис. 4-5б тот же стержень наблюдается с корпуса ракеты, движущейся со скоростью Направо. Если мы представим себе два часа, расположенные на левом и правом концах стержня, которые синхронизированы в системе стержня, относительность одновременности заставит наблюдателя в системе ракеты наблюдать (не видеть ) часы на правом конце стержня. как опережающее во времени и стержень соответственно наблюдается наклоненным. [32] : 98–99
В отличие от релятивистских эффектов второго порядка, таких как сокращение длины или замедление времени, этот эффект становится весьма значительным даже при достаточно низких скоростях. Например, это можно увидеть во вращении движущихся частиц , где прецессия Томаса представляет собой релятивистскую поправку, применимую к вращению элементарной частицы или к вращению макроскопического гироскопа , связывающую угловую скорость вращения частицы, следующей за криволинейной орбиты к угловой скорости орбитального движения. [32] : 169–174
Вращение Томаса дает разрешение известного «парадокса метровой палочки и отверстия». [стр. 15] [32] : 98–99
движения быстрее света и запрет Причинность

На рис. 4-6 временной интервал между событиями A («причина») и B («следствие») «времяподобен»; то есть существует система отсчета, в которой события A и B происходят в одном и том же месте пространства , разделенные только тем, что происходят в разное время. Если A предшествует B в этом кадре, то A предшествует B во всех кадрах, доступных с помощью преобразования Лоренца. Материя (или информация) может путешествовать (со скоростью ниже скорости света) из места А, начиная с момента А, до места Б, прибывая в момент Б, поэтому может существовать причинно-следственная связь ( где А является причиной, а Б — следствием).
Интервал AC на диаграмме «пространственный»; то есть существует система отсчета, в которой события А и С происходят одновременно, разделенные только пространством. Существуют также кадры, в которых A предшествует C (как показано), и кадры, в которых C предшествует A. Но с помощью преобразования Лоренца не доступны кадры, в которых события A и C происходят в одном и том же месте. Если бы между событиями А и С существовала причинно-следственная связь, это привело бы к парадоксам причинности.
Например, если бы сигналы можно было отправлять быстрее света, то сигналы можно было бы отправлять в прошлое отправителя (наблюдатель Б на диаграммах). [46] [стр. 16] Тогда можно было бы построить множество причинно-следственных парадоксов.
Рассмотрим пространственно-временные диаграммы на рис. 4-7. A и B стоят рядом с железнодорожными путями, когда мимо проезжает высокоскоростной поезд: C едет в последнем вагоне поезда, а D - в ведущем вагоне. Мировые линии A и B вертикальны ( ct ), что отличает стационарное положение этих наблюдателей на земле, тогда как мировые линии C и D наклонены вперед ( ct ' ), отражая быстрое движение наблюдателей C и D. стоят в своем поезде, если смотреть с земли.
- Рис. 4-7а. Событие «B передает сообщение D», когда ведущая машина проезжает мимо, находится в начале кадра D. D отправляет сообщение по поезду C в заднем вагоне, используя вымышленный «мгновенный коммуникатор». Мировая линия этого сообщения — толстая красная стрелка, идущая вдоль ось, которая представляет собой линию одновременности в заштрихованных кадрах C и D. В (нештрихованном) наземном кадре сигнал поступает раньше, чем был отправлен.
- Рис. 4-7б. Событие «C, передающее сообщение А», стоящему у железнодорожных путей, находится в начале их кадров. Теперь А отправляет сообщение по путям Б через «мгновенный коммуникатор». Мировая линия этого послания — синяя жирная стрелка, идущая вдоль ось, которая представляет собой линию одновременности для кадров A и B. Как видно из пространственно-временной диаграммы, B получит сообщение до того, как отправит его, что является нарушением причинности. [47]
Сигналы не обязательно должны быть мгновенными, чтобы нарушить причинно-следственную связь. Даже если сигнал от D до C был немного меньше, чем сигнал оси (и сигнал от A до B немного круче, чем оси), у B все равно будет возможность получить свое сообщение до того, как он его отправит. Увеличив скорость поезда почти до скорости света, и оси можно сжать очень близко к пунктирной линии, представляющей скорость света. С помощью этой модифицированной установки можно продемонстрировать, что даже сигналы, скорость которых лишь немного превышает скорость света, приведут к нарушению причинно-следственной связи. [48]
Следовательно, если причинность необходимо сохранить , одним из следствий специальной теории относительности является то, что ни один информационный сигнал или материальный объект не может перемещаться быстрее света в вакууме.
Это не значит, что все скорости, превышающие скорость света, невозможны. Можно описать различные тривиальные ситуации, когда некоторые «вещи» (не реальная материя или энергия) движутся быстрее света. [49] Например, место, где луч прожектора попадает на нижнюю часть облака, может двигаться быстрее, чем свет, если прожектор быстро поворачивать (хотя это не нарушает причинно-следственной связи или любого другого релятивистского явления). [50] [51]
Оптические эффекты [ править ]
Перетаскивание эффектов [ править ]

В 1850 году Ипполит Физо и Леон Фуко независимо друг от друга установили, что свет распространяется медленнее в воде, чем в воздухе, тем самым подтвердив предсказание Френеля волновой теории света Ньютона и опровергнув соответствующее предсказание корпускулярной теории . [52] Скорость света измеряли в стоячей воде. Какова будет скорость света в текущей воде?
Чтобы ответить на этот вопрос, в 1851 году Физо провел эксперимент, упрощенное изображение которого показано на рис. 5-1. Луч света разделяется светоделителем, и разделенные лучи проходят в противоположных направлениях через трубку с текущей водой. Они рекомбинируются, образуя интерференционные полосы, указывающие на разницу в длине оптического пути, которую может видеть наблюдатель. Эксперимент продемонстрировал, что перетаскивание света текущей водой вызывало смещение полос, показывая, что движение воды повлияло на скорость света.
Согласно теориям, преобладавшим в то время, свет, проходящий через движущуюся среду, был бы простой суммой его скорости в этой среде плюс скорость самой среды. Вопреки ожиданиям, Физо обнаружил, что, хотя казалось, что свет увлекается водой, величина этого сопротивления была намного ниже, чем ожидалось. Если - скорость света в стоячей воде, а скорость воды, а - это скорость света в воде в лабораторных условиях, при этом поток воды добавляется к скорости света или вычитается из нее, тогда
Результаты Физо, хотя и согласовывались с более ранней гипотезой Френеля о частичном увлечении эфира , крайне смутили физиков того времени. Помимо прочего, наличие члена показателя преломления означало, что, поскольку В зависимости от длины волны эфир должен быть способен поддерживать разные движения одновременно. [примечание 8] было предложено множество теоретических объяснений Для объяснения коэффициента сопротивления Френеля , которые полностью противоречили друг другу. Еще до эксперимента Майкельсона-Морли результаты экспериментов Физо входили в число наблюдений, создавших критическую ситуацию в объяснении оптики движущихся тел. [53]
С точки зрения специальной теории относительности результат Физо представляет собой не что иное, как приближение к уравнению 10 , релятивистской формуле композиции скоростей. [31]
света Релятивистская аберрация

Из-за конечной скорости света, если относительные движения источника и приемника включают поперечную составляющую, то направление, откуда свет попадает в приемник, будет смещено от геометрического положения в пространстве источника относительно приемника. Классический расчет смещения принимает две формы и дает разные прогнозы в зависимости от того, движутся ли приемник, источник или оба они относительно среды. (1) Если приемник находится в движении, смещение будет следствием аберрации света . Угол падения луча относительно приемника можно рассчитать по векторной сумме движений приемника и скорости падающего света. [54] (2) Если источник находится в движении, смещение будет следствием коррекции светового времени . Смещение видимого положения источника от его геометрического положения будет результатом движения источника в течение времени, которое требуется его свету, чтобы достичь приемника. [55]
Классическое объяснение не прошло экспериментальную проверку. Поскольку угол аберрации зависит от соотношения скорости приемника и скорости падающего света, прохождение падающего света через преломляющую среду должно изменить угол аберрации. В 1810 году Араго использовал это ожидаемое явление в неудачной попытке измерить скорость света. [56] а в 1870 году Джордж Эйри проверил эту гипотезу с помощью телескопа, наполненного водой, и обнаружил, что, вопреки ожиданиям, измеренная аберрация была идентична аберрации, измеренной с помощью телескопа, наполненного воздухом. [57] «Громоздкая» попытка объяснить эти результаты использовала гипотезу частичного сопротивления эфира. [58] но было несовместимо с результатами эксперимента Майкельсона-Морли, который, очевидно, требовал полного сопротивления эфира. [59]
Предполагая инерциальную систему отсчета, релятивистское выражение для аберрации света применимо как к случаю движения приемника, так и к случаю движения источника. Было опубликовано множество тригонометрически эквивалентных формул. Выраженные через переменные на рис. 5-2, они включают в себя [31] : 57–60
- ИЛИ ИЛИ
Доплера Релятивистский эффект
Доплера Релятивистский продольный эффект
Классический эффект Доплера зависит от того, движутся ли источник, приемник или оба относительно среды. Релятивистский эффект Доплера не зависит от какой-либо среды. Тем не менее, релятивистский доплеровский сдвиг для продольного случая, когда источник и приемник движутся прямо навстречу или друг от друга, может быть получен так же, как если бы это было классическое явление, но модифицированное добавлением члена замедления времени , и это трактовка описано здесь. [60] [61]
Предположим, что приемник и источник удаляются друг от друга с относительной скоростью измеренное наблюдателем на приемнике или источнике (принятое здесь соглашение о знаках заключается в том, что отрицательно , если приемник и источник движутся навстречу друг другу). Предположим, что источник неподвижен в среде. Затем
Для света и при движении приемника с релятивистскими скоростями часы на приемнике замедляются по времени относительно часов на источнике. Приемник будет измерять принимаемую частоту, чтобы
- и
- является фактором Лоренца .
Идентичное выражение для релятивистского доплеровского сдвига получается при проведении анализа в системе отсчёта приёмника с движущимся источником. [62] [21]
Поперечный эффект Доплера [ править ]

Поперечный эффект Доплера — одно из главных новых предсказаний специальной теории относительности.
Классически можно было бы ожидать, что если источник и приемник движутся поперечно друг другу без продольной составляющей их относительных движений, то не должно быть доплеровского сдвига в свете, поступающем на приемник.
Специальная теория относительности предсказывает обратное. На рис. 5-3 показаны два распространенных варианта этого сценария. Оба варианта можно проанализировать, используя простые аргументы замедления времени. [21] На рис. 5-3а приемник наблюдает свет от источника как сдвинутый в голубую сторону в раз. . На рис. 5-3б свет смещен в красную сторону на тот же коэффициент.
Измерение и внешний вид [ править ]

Замедление времени и сокращение длины — это не оптические иллюзии, а настоящие эффекты. Измерения этих эффектов не являются артефактом доплеровского сдвига и не являются результатом игнорирования времени, которое требуется свету, чтобы пройти путь от события до наблюдателя.
Ученые проводят фундаментальное различие между измерением или наблюдением, с одной стороны, и визуальным внешним видом , или тем, что человек видит . Измеренная форма объекта представляет собой гипотетический снимок всех точек объекта в том виде, в котором они существуют в определенный момент времени. Но на внешний вид объекта влияет разная продолжительность времени, которое требуется свету, чтобы пройти от разных точек объекта до глаза.

В течение многих лет различие между этими двумя объектами обычно не осознавалось, и обычно считалось, что объект с уменьшенной длиной, проходящий мимо наблюдателя, на самом деле будет рассматриваться как уменьшенный по длине. В 1959 году Джеймс Террелл и Роджер Пенроуз независимо друг от друга отметили, что эффекты дифференциальной задержки во времени в сигналах, достигающих наблюдателя из разных частей движущегося объекта, приводят к тому, что внешний вид быстро движущегося объекта сильно отличается от его измеренной формы. Например, удаляющийся объект будет казаться сжатым, приближающийся объект будет выглядеть удлиненным, а проходящий объект будет иметь перекошенный вид, который можно сравнить с вращением. [стр. 19] [стр. 20] [63] [64] Сфера в движении сохраняет круговой контур при любой скорости, на любом расстоянии и при всех углах обзора, хотяповерхность сферы и изображения на ней будут казаться искаженными. [65] [66]

На рисунках 5-4 и 5-5 показаны объекты, движущиеся поперек луча зрения. На рис. 5-4 куб рассматривается с расстояния, в четыре раза превышающего длину его сторон. На высоких скоростях стороны куба, перпендикулярные направлению движения, приобретают гиперболическую форму. Куб на самом деле не вращается. Скорее, свету из задней части куба требуется больше времени, чтобы достичь глаз, по сравнению со светом спереди, за это время куб сместился вправо. На больших скоростях сфера на рис. 5-5 принимает вид сплюснутого диска, наклоненного до 45° от луча зрения. Если движения объектов не являются строго поперечными, а включают продольный компонент, можно увидеть преувеличенные искажения перспективы. [67] Эта иллюзия стала известна как вращение Террелла или эффект Террелла-Пенроуза . [примечание 9]
Другой пример, когда внешний вид расходится с измерениями, связан с наблюдением кажущегося сверхсветового движения в различных радиогалактиках , объектах BL Lac , квазарах и других астрономических объектах, которые выбрасывают струи материи с релятивистской скоростью под узкими углами по отношению к зрителю. В результате возникает кажущаяся оптическая иллюзия, создающая видимость перемещения со скоростью, превышающей скорость света. [68] [69] [70] На рис. 5-6 галактика M87 выбрасывает высокоскоростную струю субатомных частиц почти прямо к нам, но вращение Пенроуза-Террелла заставляет струю двигаться вбок таким же образом, как и куб на рис. .5-4 был растянут. [71]
Динамика [ править ]
Раздел « Следствия, вытекающие из преобразования Лоренца», посвящен исключительно кинематике , изучению движения точек, тел и систем тел без учета сил, вызвавших движение. В этом разделе обсуждаются массы, силы, энергия и т. д., поэтому требуется рассмотрение физических эффектов, выходящих за рамки самого преобразования Лоренца.
Эквивалентность массы и энергии [ править ]
Когда скорость объекта приближается к скорости света с точки зрения наблюдателя, его релятивистская масса увеличивается, что затрудняет его ускорение из системы отсчета наблюдателя.
Энергетическое содержание покоящегося объекта массой m равно mc 2 . Сохранение энергии означает, что в любой реакции уменьшение суммы масс частиц должно сопровождаться увеличением кинетических энергий частиц после реакции. Точно так же массу объекта можно увеличить, приняв кинетическую энергию.
В дополнение к упомянутым выше статьям, в которых даны выводы преобразования Лоренца и описываются основы специальной теории относительности, Эйнштейн также написал по крайней мере четыре статьи, дающие эвристические аргументы в пользу эквивалентности (и трансмутальности) массы и энергии, для E = mc 2 .
Эквивалентность массы и энергии является следствием специальной теории относительности. Энергия и импульс, которые в ньютоновской механике разделены, образуют в теории относительности четырехвектор , и это нетривиальным образом связывает временную составляющую (энергию) с пространственными компонентами (импульс). Для покоящегося объекта четырехвектор энергии-импульса равен ( E / c , 0, 0, 0) : он имеет временной компонент, который является энергией, и три пространственных компонента, которые равны нулю. Путем смены кадров с преобразованием Лоренца в направлении x с малым значением скорости v четырехвектор энергии-импульса становится ( E / c , Ev / c 2 , 0, 0) . Импульс равен энергии, умноженной на скорость, деленную на c 2 . Таким образом, ньютоновская масса объекта, которая представляет собой отношение импульса к скорости для медленных скоростей, равна E / c. 2 .
Энергия и импульс являются свойствами материи и излучения, и невозможно сделать вывод, что они образуют четырехвектор только из двух основных постулатов специальной теории относительности, потому что они не говорят о материи или излучении, они говорят только о пространство и время. Поэтому вывод требует некоторых дополнительных физических рассуждений. В своей статье 1905 года Эйнштейн использовал дополнительные принципы, которые механика Ньютона должна соблюдать для медленных скоростей, так что существует один скаляр энергии и один трехвекторный импульс на медленных скоростях, и что закон сохранения энергии и импульса в точности верен в теории относительности. . Более того, он предположил, что энергия света преобразуется под действием того же коэффициента доплеровского сдвига, что и его частота, что он ранее доказал на основе уравнений Максвелла. [стр 1] Первой из статей Эйнштейна на эту тему была «Зависит ли инерция тела от содержания в нем энергии?» в 1905 году. [стр. 21] Хотя аргумент Эйнштейна в этой статье почти повсеместно принят физиками как правильный и даже самоочевидный, многие авторы на протяжении многих лет предполагали, что он неверен. [72] Другие авторы предполагают, что этот аргумент был просто неубедительным, поскольку основывался на некоторых неявных предположениях. [73]
Эйнштейн признал разногласия по поводу своего вывода в своей обзорной статье по специальной теории относительности 1907 года. Там он отмечает, что проблематично полагаться на уравнения Максвелла для эвристического аргумента масса-энергия. Аргументация в его статье 1905 года может быть проведена с испусканием любых безмассовых частиц, но уравнения Максвелла неявно используются, чтобы сделать очевидным, что испускание света, в частности, может быть достигнуто только путем совершения работы. Чтобы излучать электромагнитные волны, все, что вам нужно сделать, это встряхнуть заряженную частицу, и это явно совершает работу, так что излучение имеет энергию. [стр. 22] [примечание 10]
Демонстрация Эйнштейном равенства E = mc в 1905 году. 2 [ редактировать ]
В своей четвертой из своих Annus mirabilis 1905 года статей [стр. 21] Эйнштейн представил эвристический аргумент в пользу эквивалентности массы и энергии. Хотя, как обсуждалось выше, последующие исследования установили, что его аргументы не получили в целом окончательного доказательства, выводы, к которым он пришел в этой статье, выдержали испытание временем.
Эйнштейн взял в качестве исходных предположений свою недавно открытую формулу релятивистского доплеровского сдвига , законы сохранения энергии и сохранения импульса , а также взаимосвязь между частотой света и его энергией, подразумеваемую уравнениями Максвелла .
Рис. 6-1 (вверху). Рассмотрим систему плоских волн света с частотой путешествуя в направлении относительно оси x системы S. отсчета Частота (и, следовательно, энергия) волн, измеренная в системе отсчета S ′ , которая движется вдоль оси x со скоростью задается релятивистской формулой доплеровского сдвига, которую Эйнштейн разработал в своей статье 1905 года по специальной теории относительности: [стр 1]
Рис. 6-1 (внизу). стационарное в системе отсчета S. Рассмотрим произвольное тело , Пусть это тело излучает пару световых импульсов одинаковой энергии в противоположных направлениях под углом относительно оси х. Каждый импульс имеет энергию . Из-за сохранения импульса тело остается неподвижным в S после излучения двух импульсов. Позволять быть энергией тела до испускания двух импульсов и после их выброса.
Далее рассмотрим ту же систему, наблюдаемую из системы отсчета S ′ , которая движется вдоль оси x со скоростью относительно S. кадра В этом кадре свет от прямых и обратных импульсов будет иметь релятивистский доплеровский сдвиг. Позволять быть энергией тела, измеренной в системе отсчета S ' до испускания двух импульсов и после их выброса. Получаем следующие соотношения: [стр. 21]
Из приведенных выше уравнений получаем следующее:
| ( 6-1 ) |
Два различия формы наблюдаемые в приведенном выше уравнении, имеют простую физическую интерпретацию. С и – энергии произвольного тела в движущейся и неподвижной системах отсчета, и представляет собой кинетические энергии тел до и после испускания света (за исключением аддитивной константы, фиксирующей нулевую точку энергии и обычно приравниваемой к нулю). Следовательно,
| ( 6-2 ) |
Разложив ряд Тейлора и пренебрегая членами более высокого порядка, он получил
| ( 6-3 ) |
Сравнивая приведенное выше выражение с классическим выражением для кинетической энергии, KE = 1/2 2мВ 2 Эйнштейн тогда заметил: «Если тело отдает энергию L в виде излучения, его масса уменьшается на L/c 2 ."
Риндлер заметил, что эвристический аргумент Эйнштейна предполагает лишь то, что энергия способствует увеличению массы. В 1905 году осторожное выражение Эйнштейном соотношения массы и энергии допускало возможность существования «спящей» массы, которая останется после того, как вся энергия тела будет удалена. Однако к 1907 году Эйнштейн был готов утверждать, что вся инертная масса представляет собой запас энергии. «Чтобы приравнять всю массу к энергии, потребовался акт эстетической веры, очень характерный для Эйнштейна». [12] : 81–84 Смелая гипотеза Эйнштейна получила широкое подтверждение в годы, последовавшие за его первоначальным предложением.
По ряду причин первоначальный вывод Эйнштейна в настоящее время редко преподается. Помимо продолжающихся до сих пор энергичных дебатов относительно формальной правильности его первоначального вывода, признание специальной теории относительности тем, что Эйнштейн называл «принципиальной теорией», привело к переходу от использования электромагнитных явлений к чисто динамическим методам исследования. доказательство. [74]
Упругие столкновения [ править ]
Изучение продуктов столкновений, генерируемых ускорителями частиц по всему миру, дает ученым доказательства структуры субатомного мира и естественных законов, управляющих им. Анализ продуктов столкновений, сумма масс которых может значительно превышать массы налетающих частиц, требует специальной теории относительности. [75]
В ньютоновской механике анализ столкновений предполагает использование законов сохранения массы , импульса и энергии . В релятивистской механике масса не сохраняется независимо, поскольку она включена в полную релятивистскую энергию. Мы иллюстрируем различия, возникающие между ньютоновской и релятивистской трактовкой столкновений частиц, на примере простого случая двух совершенно упругих сталкивающихся частиц одинаковой массы. ( Неупругие столкновения обсуждаются в разделе «Законы сохранения пространства-времени» . Радиоактивный распад можно рассматривать как своего рода неупругое столкновение, обращенное во времени. [75] )
Упругое рассеяние заряженных элементарных частиц отклоняется от идеальности из-за возникновения тормозного излучения. [76] [77]
Ньютоновский анализ [ править ]

На рис. 6-2 демонстрируется результат, знакомый игрокам в бильярд: если по неподвижному шару упруго ударяет другой шар такой же массы (при условии отсутствия бокового вращения, или «английского»), то после столкновения расходящиеся траектории из двух шаров будет составлять прямой угол. (а) В стационарной системе отсчета падающая сфера, движущаяся под углом 2 v, сталкивается с неподвижной сферой. (б) В центре системы импульса две сферы приближаются друг к другу симметрично при ± v . После упругого столкновения две сферы отскакивают друг от друга с равными и противоположными скоростями ± u . Сохранение энергии требует, чтобы |u| = |v|. (c) Возвращаясь к стационарной системе отсчета, скорости отскока равны v ± u. Скалярное произведение ( v + u ) • ( v - u ) = v 2 - в 2 = 0, что указывает на то, что векторы ортогональны. [12] : 26–27
анализ Релятивистский

Рассмотрим сценарий упругого столкновения на рис. 6-3 между движущейся частицей и неподвижной частицей равной массы. В отличие от ньютоновского случая, угол между двумя частицами после столкновения составляет менее 90 °, зависит от угла рассеяния и становится все меньше и меньше по мере того, как скорость падающей частицы приближается к скорости света:
Релятивистский импульс и полная релятивистская энергия частицы определяются выражениями
| ( 6-4 ) |
Сохранение импульса требует, чтобы сумма импульсов входящей частицы и неподвижной частицы (которая изначально имела импульс = 0) равна сумме импульсов вылетающих частиц:
| ( 6-5 ) |
Аналогично, сумма полных релятивистских энергий влетающей частицы и неподвижной частицы (которая изначально имеет полную энергию mc 2 ) равна сумме полных энергий вылетевших частиц:
| ( 6-6 ) |
Разбивка ( 6-5 ) на составные части, замена с безразмерным и исключение общих терминов из ( 6-5 ) и ( 6-6 ) дает следующее: [стр. 23]
| ( 6-7 ) |
| ( 6-8 ) |
| ( 6-9 ) |
Из них мы получаем следующие соотношения: [стр. 23]
| ( 6-10 ) |
| ( 6-11 ) |
| ( 6-12 ) |
Для симметричного случая, когда и ( 6-12 ) принимает более простой вид: [стр. 23]
| ( 6-13 ) |
Как далеко можно путешествовать от Земли? [ редактировать ]
Поскольку ничто не может двигаться быстрее света, можно заключить, что человек никогда не сможет путешествовать от Земли дальше, чем на ~100 световых лет. Вы легко могли бы подумать, что путешественник никогда не сможет достичь большего, чем несколько солнечных систем, которые существуют в пределах 100 световых лет от Земли. Однако из-за замедления времени гипотетический космический корабль может путешествовать на тысячи световых лет за время жизни пассажира. Если бы можно было построить космический корабль, который ускорялся бы с постоянной скоростью 1 g , через год он будет двигаться почти со скоростью света, наблюдаемой с Земли. Это описано:
где v ( t ) — скорость в момент времени t , a — ускорение космического корабля, а t — координатное время, измеренное людьми на Земле. [стр. 24] Следовательно, после года ускорения до 9,81 м/с 2 , космический корабль будет двигаться со скоростью v = 0,712 c и 0,946 c через три года относительно Земли. После трех лет такого ускорения, когда космический корабль достигнет скорости 94,6% скорости света относительно Земли, замедление времени приведет к тому, что каждая секунда, испытываемая на космическом корабле, будет соответствовать 3,1 секунды на Земле. Во время своего путешествия люди на Земле будут испытывать больше времени, чем они, поскольку их часы (все физические явления) действительно будут идти в 3,1 раза быстрее, чем часы на космическом корабле. Пятилетнее путешествие туда и обратно у путешественника займет 6,5 земных лет и преодолеет расстояние более 6 световых лет. 20-летнее путешествие туда и обратно (5 лет с ускорением, 5 с замедлением, дважды каждый) вернет их на Землю, пройдя 335 земных лет и расстояние в 331 световой год. [78] Полное 40-летнее путешествие при массе 1 g продлится на Земле 58 000 лет и охватит расстояние в 55 000 световых лет. 40-летнее путешествие при массе 1,1 g займет 148 000 земных лет и охватит около 140 000 световых лет. 28-летнее путешествие в одну сторону (14 лет с ускорением и 14 с замедлением по часам астронавта) при ускорении 1 g может достичь 2 000 000 световых лет до Галактики Андромеды. [78] Это же замедление времени является причиной того, что мюон, путешествующий близко к c , путешествует намного дальше, чем c, умноженное на его период полураспада (в состоянии покоя). [79]
относительности и объединяющий Теория электромагнетизм
Теоретические исследования классического электромагнетизма привели к открытию распространения волн. Уравнения, обобщающие электромагнитные эффекты, показали, что конечная скорость распространения полей E и B требует определенного поведения заряженных частиц. Общее исследование движущихся зарядов формирует потенциал Льенара-Вихерта , что является шагом к специальной теории относительности.
Лоренцево преобразование электрического поля движущегося заряда в систему отсчета неподвижного наблюдателя приводит к появлению математического термина, обычно называемого магнитным полем . И наоборот, магнитное поле, создаваемое движущимся зарядом, исчезает и становится чисто электростатическим полем в сопутствующей системе отсчета. Таким образом, уравнения Максвелла представляют собой просто эмпирическую адаптацию специальных релятивистских эффектов в классической модели Вселенной. Поскольку электрические и магнитные поля зависят от системы отсчета и, таким образом, переплетаются, говорят об электромагнитных полях. Специальная теория относительности предоставляет правила преобразования того, как электромагнитное поле в одной инерциальной системе координат появляется в другой инерциальной системе отсчета.
Уравнения Максвелла в трехмерной форме уже согласуются с физическим содержанием специальной теории относительности, хотя ими легче манипулировать в явно ковариантной форме, то есть на языке тензорного исчисления. [80]
Теории относительности и квантовая механика [ править ]
Специальная теория относительности может быть объединена с квантовой механикой, образуя релятивистскую квантовую механику и квантовую электродинамику . Как общую теорию относительности можно объединить и квантовую механику — одна из нерешенных проблем физики ; квантовая гравитация и « теория всего », которые требуют объединения, включая и общую теорию относительности, являются активными и постоянными областями теоретических исследований.
Ранняя атомная модель Бора-Зоммерфельда объясняла тонкую структуру атомов щелочных металлов, используя как специальную теорию относительности, так и предварительные знания по квантовой механике того времени. [81]
В 1928 году Поль Дирак построил влиятельное релятивистское волновое уравнение , теперь известное в его честь как уравнение Дирака . [стр. 25] которое полностью совместимо как со специальной теорией относительности, так и с окончательной версией квантовой теории, существовавшей после 1926 года. Это уравнение не только описывало собственный угловой момент электронов, называемый спином , но также привело к предсказанию античастицы электрона ( позитрона) . ), [стр. 25] [стр. 26] а тонкую структуру можно было полностью объяснить только с помощью специальной теории относительности. Это было первое основание релятивистской квантовой механики .
С другой стороны, существование античастиц приводит к выводу, что релятивистской квантовой механики недостаточно для более точной и полной теории взаимодействия частиц. Вместо этого становится необходимой теория частиц, интерпретируемых как квантованные поля, называемая квантовой теорией поля ; в котором частицы могут создаваться и уничтожаться в пространстве и времени.
Статус [ править ]
Специальная теория относительности в пространстве-времени Минковского точна только тогда, когда абсолютное значение гравитационного потенциала намного меньше c 2 в интересующем регионе. [82] В сильном гравитационном поле приходится пользоваться общей теорией относительности . Общая теория относительности становится специальной теорией относительности на пределе слабого поля. На очень малых масштабах, например планковской длине и ниже, необходимо учитывать квантовые эффекты, приводящие к квантовой гравитации . Но на макроскопических масштабах и в отсутствие сильных гравитационных полей специальная теория относительности экспериментально проверяется с чрезвычайно высокой степенью точности (10 −20 ) [83] и таким образом принят физическим сообществом. Экспериментальные результаты, которые кажутся противоречащими этому, не воспроизводимы и поэтому широко полагают, что они обусловлены экспериментальными ошибками.
Специальная теория относительности математически самосогласована и является органической частью всех современных физических теорий, особенно квантовой теории поля , теории струн и общей теории относительности (в предельном случае пренебрежимо малых гравитационных полей).
Механика Ньютона математически следует из специальной теории относительности при малых скоростях (по сравнению со скоростью света) – таким образом, механику Ньютона можно рассматривать как специальную теорию относительности медленно движущихся тел. см . В классической механике Более подробное обсуждение .
Несколько экспериментов, предшествовавших статье Эйнштейна 1905 года, теперь интерпретируются как доказательство теории относительности. Из них известно, что Эйнштейну было известно об эксперименте Физо до 1905 года. [84] и историки пришли к выводу, что Эйнштейн, по крайней мере, знал об эксперименте Майкельсона-Морли еще в 1899 году, несмотря на заявления, которые он делал в последние годы своей жизни, что он не сыграл никакой роли в разработке им теории. [16]
- Эксперимент Физо (1851 г., повторенный Майкельсоном и Морли в 1886 г.) измерял скорость света в движущихся средах, результаты которого согласуются с релятивистским сложением коллинеарных скоростей.
- Знаменитый эксперимент Майкельсона-Морли (1881, 1887) дал дальнейшее подтверждение постулату о невозможности обнаружения абсолютной эталонной скорости. Здесь следует отметить, что, вопреки многим альтернативным утверждениям, здесь мало что говорится об инвариантности скорости света по отношению к скорости источника и наблюдателя, поскольку и источник, и наблюдатель всегда двигались вместе с одной и той же скоростью.
- Эксперимент Траутона -Нобла (1903 г.) показал, что крутящий момент на конденсаторе не зависит от положения и инерциальной системы отсчета.
- Опыты Рэлея и Брейса (1902, 1904) показали, что сокращение длины не приводит к двойному лучепреломлению для попутного наблюдателя в соответствии с принципом относительности.
Ускорители частиц ускоряют и измеряют свойства частиц, движущихся со скоростью, близкой к скорости света, где их поведение согласуется с теорией относительности и несовместимо с более ранней ньютоновской механикой . Эти машины просто не работали бы, если бы они не были спроектированы в соответствии с релятивистскими принципами. Кроме того, проведено немалое количество современных экспериментов по проверке специальной теории относительности. Некоторые примеры:
- Тесты релятивистской энергии и импульса – проверка предельной скорости частиц
- Эксперимент Айвза-Стилуэлла - проверка релятивистского эффекта Доплера и замедления времени
- Экспериментальная проверка замедления времени - релятивистское влияние на период полураспада быстродвижущихся частиц.
- Эксперимент Кеннеди-Торндайка - замедление времени в соответствии с преобразованиями Лоренца.
- Эксперимент Хьюза – Древера - проверка изотропии пространства и массы
- Современные поиски нарушения Лоренца – различные современные тесты
- Эксперименты по проверке теории излучения показали, что скорость света не зависит от скорости излучателя.
- Эксперименты по проверке гипотезы сопротивления эфира – отсутствие «препятствия потоку эфира».
обсуждение пространства времени - Техническое
Геометрия пространства-времени [ править ]
плоского евклидова пространства и Сравнение пространства Минковского

Специальная теория относительности использует «плоское» 4-мерное пространство Минковского – пример пространства-времени . Пространство-время Минковского очень похоже на стандартное трехмерное евклидово пространство , но есть существенное отличие во времени.
В трехмерном пространстве дифференциал расстояния (линейного элемента) ds определяется выражением
где d x = ( dx 1 , dx 2 , dx 3 ) — дифференциалы трех пространственных измерений. В геометрии Минковского существует дополнительное измерение с координатой X. 0 производное от времени, так что дифференциал расстояний удовлетворяет
где d X = ( dX 0 , dX 1 , dX 2 , dX 3 ) — дифференциалы четырех измерений пространства-времени. Это предполагает глубокое теоретическое понимание: специальная теория относительности — это просто вращательная симметрия нашего пространства-времени, аналогичная вращательной симметрии евклидова пространства (см. рис. 10-1). [86] Точно так же, как евклидово пространство использует евклидову метрику , пространство-время использует метрику Минковского . По сути, специальную теорию относительности можно сформулировать как инвариантность любого пространственно-временного интервала (то есть четырехмерного расстояния между любыми двумя событиями) при просмотре из любой инерциальной системы отсчета . Все уравнения и эффекты специальной теории относительности могут быть выведены из этой вращательной симметрии ( группы Пуанкаре ) пространства-времени Минковского.
Фактическая форма ds выше зависит от метрики и выбора X 0 координировать.Чтобы координата времени выглядела как координаты пространства, ее можно рассматривать как мнимую : X 0 = ict (это называется вращением Вика ).Согласно Миснеру , Торну и Уиллеру (1971, §2.3), в конечном итоге более глубокое понимание как специальной, так и общей теории относительности будет достигнуто в результате изучения метрики Минковского (описанной ниже) и принятия X 0 = ct , а не «замаскированную» евклидову метрику, использующую ict в качестве временной координаты.
Некоторые авторы используют X 0 = t с коэффициентами c в другом месте для компенсации; например, пространственные координаты делятся на c или на коэффициенты c ±2 входят в метрический тензор. [87] Эти многочисленные соглашения можно заменить использованием натуральных единиц , где c = 1 . Тогда пространство и время имеют эквивалентные единицы, и никакие факторы с нигде не появляются.
3D spacetime [ edit ]

Если мы уменьшим пространственные измерения до 2, чтобы мы могли представить физику в трехмерном пространстве
мы видим, что нулевые геодезические лежат вдоль двойственного конуса (см. рис. 10-2), определяемого уравнением;
или просто
которое представляет собой уравнение окружности радиуса c dt .
4D пространство-время [ править ]
Если мы расширим это до трех пространственных измерений, нулевые геодезические будут представлять собой 4-мерный конус:
так

Как показано на рис. 10-3, нулевые геодезические можно представить как набор непрерывных концентрических сфер с радиусами = c dt .
Этот нулевой двойной конус представляет собой «линию обзора» точки в пространстве. То есть, когда мы смотрим на звезды и говорим: «Свету от этой звезды, который я получаю, X лет», мы смотрим на эту линию зрения: нулевую геодезическую. Мы смотрим на событие на расстоянии далеко и время d/c в прошлом. По этой причине нулевой двойной конус также известен как «световой конус». (Точка в левом нижнем углу рисунка 10-2 представляет звезду, начало координат представляет наблюдателя, а линия представляет собой нулевую геодезическую «линию зрения».)
Конус в области – t — это информация, которую точка «получает», а конус в разделе + t — это информация, которую точка «отправляет».
Геометрию пространства Минковского можно изобразить с помощью диаграмм Минковского , которые также полезны для понимания многих мысленных экспериментов в специальной теории относительности.
Физика в пространстве-времени [ править ]
Преобразования физических величин между системами отсчета [ править ]
Выше преобразование Лоренца для временной координаты и трех пространственных координат показывает, что они переплетаются. Это верно в более общем плане: определенные пары «времяподобных» и «пространственноподобных» величин естественным образом объединяются на равных основаниях при одном и том же преобразовании Лоренца.
Преобразование Лоренца в стандартной конфигурации, указанной выше, то есть для повышения в направлении x , можно преобразовать в матричную форму следующим образом:
В ньютоновской механике величины, имеющие величину и направление, математически описываются как трехмерные векторы в евклидовом пространстве и, как правило, параметризуются временем. В специальной теории относительности это понятие расширяется за счет добавления соответствующей времениподобной величины к пространственноподобной векторной величине, и мы имеем 4D-векторы, или « четыре-векторы », в пространстве-времени Минковского. Компоненты векторов записываются с использованием тензорной индексной нотации , поскольку это имеет множество преимуществ. Обозначения проясняют, что уравнения явно ковариантны относительно группы Пуанкаре , что позволяет избежать утомительных вычислений для проверки этого факта. При построении таких уравнений мы часто обнаруживаем, что уравнения, которые раньше считались несвязанными, на самом деле тесно связаны, являясь частью одного и того же тензорного уравнения. других физических величин тензорами Признание упрощает законы их преобразования. Везде верхние индексы (верхние индексы) являются контравариантными индексами, а не экспонентами, за исключением случаев, когда они обозначают квадрат (это должно быть ясно из контекста), а нижние индексы (нижние индексы) являются ковариантными индексами. Для простоты и согласованности с предыдущими уравнениями будут использоваться декартовы координаты.
Простейшим примером четырехвектора является положение события в пространстве-времени, которое представляет собой времениподобный компонент ct и пространственноподобный компонент x = ( x , y , z ) в контравариантном положения четырехвекторе с компонентами:
где имеется подразумеваемое суммирование по от 0 до 3, и является матрицей .
В более общем смысле, все контравариантные компоненты четырехвектора преобразовать один кадр в другой с помощью преобразования Лоренца :
Примеры других 4-векторов включают четырехскоростной определяется как производная 4-вектора положения по собственному времени :
Релятивистская энергия и релятивистский импульс объекта являются соответственно времениподобными и пространственноподобными компонентами контравариантного вектора четырехимпульса :
Четырех -ускорение является собственной производной по времени от 4-скорости:
Правила преобразования трехмерных скоростей и ускорений очень неудобны; даже выше в стандартной конфигурации уравнения скорости весьма сложны из-за своей нелинейности. С другой стороны, преобразование четырех -скорости и четырех -ускорения проще с помощью матрицы преобразования Лоренца.
Четырехградиент φ преобразуется ковариантно , скалярного поля а не контравариантно:
что является транспонированием:
только в декартовых координатах. Это ковариантная производная , которая преобразуется в явную ковариацию, в декартовых координатах это сводится к частным производным, но не в других координатах.
В более общем смысле, ковариантные компоненты 4-векторного преобразования согласно обратному преобразованию Лоренца:
Постулаты специальной теории относительности ограничивают точную форму, которую принимают матрицы преобразования Лоренца.
(компоненты) В более общем смысле, большинство физических величин лучше всего описать как тензоры . Итак, для преобразования из одного кадра в другой мы используем известный закон тензорного преобразования. [91]
Примером четырехмерного антисимметричного тензора второго порядка является релятивистский угловой момент , который имеет шесть компонентов: три — классический угловой момент , а остальные три связаны с усилением центра масс системы. Производная релятивистского углового момента по собственному времени — это релятивистский крутящий момент, также антисимметричный тензор второго порядка .
Тензор электромагнитного поля второго порядка — это еще один антисимметричный тензор с шестью компонентами: три для электрического поля и еще три для магнитного поля . Существует также тензор энергии-импульса для электромагнитного поля, а именно электромагнитный тензор энергии-напряжения .
Метрика [ править ]
Метрический тензор позволяет определить скалярное произведение двух векторов, что, в свою очередь, позволяет присвоить вектору величину. Учитывая четырехмерную природу пространства-времени, метрика Минковского η имеет компоненты (действительные с правильно выбранными координатами), которые можно расположить в матрице 4 × 4 :
Группа Пуанкаре — наиболее общая группа преобразований, сохраняющая метрику Минковского:
и это физическая симметрия, лежащая в основе специальной теории относительности.
Метрику можно использовать для повышения и понижения индексов векторов и тензоров. Инварианты можно построить с использованием метрики, скалярное произведение 4-вектора T с другим 4-вектором S равно:
Инвариант означает, что он принимает одно и то же значение во всех инерциальных системах отсчета, поскольку он является скаляром (тензор ранга 0), и поэтому Λ в его тривиальном преобразовании не появляется . Величина 4-вектора T представляет собой положительный квадратный корень из внутреннего произведения самого себя:
Эту идею можно распространить на тензоры более высокого порядка, для тензора второго порядка можно сформировать инварианты:
и Релятивистская инвариантность кинематика
Координатные дифференциалы преобразуются также контрвариантно:
4-скоростной U м имеет инвариантную форму:
и Релятивистская инвариантность динамика
Инвариантная величина 4-вектора импульса порождает соотношение энергия-импульс :
Мы можем выяснить, что представляет собой этот инвариант, сначала доказав, что, поскольку он является скаляром, не имеет значения, в какой системе отсчета мы его вычисляем, а затем преобразуя его в систему отсчета, в которой полный импульс равен нулю.
Мы видим, что энергия покоя является независимым инвариантом. Энергию покоя можно вычислить даже для частиц и систем, находящихся в движении, путем перевода в систему отсчета, в которой импульс равен нулю.
Оставшаяся энергия связана с массой согласно знаменитому уравнению, обсуждавшемуся выше:
Масса систем, измеренная в их центре системы импульса (где общий импульс равен нулю), определяется полной энергией системы в этой системе отсчета. Она может не быть равна сумме масс отдельных систем, измеренных в других системах отсчета.
Чтобы использовать третий закон движения Ньютона , обе силы должны быть определены как скорость изменения импульса относительно одной и той же временной координаты. То есть для этого требуется 3D-сила, определенная выше. К сожалению, в 4D не существует тензора, который среди своих компонент содержал бы компоненты вектора 3D силы.
Если частица не движется в точке c , можно преобразовать трехмерную силу из системы отсчета, движущейся вместе с частицей, в систему отсчета наблюдателя. Это дает 4-вектор, называемый четырехсилой . Это скорость изменения указанного выше четырехвектора энергии - импульса относительно собственного времени. Ковариантная версия четырех сил:
В системе покоя объекта временная составляющая четырех сил равна нулю, если только « инвариантная масса » объекта не меняется (для этого требуется незамкнутая система, в которой энергия/масса напрямую добавляется или удаляется из системы). объекта), и в этом случае это отрицательное значение скорости изменения массы, умноженное на c . Однако в целом компоненты четырехсилы не равны компонентам трехсилы, поскольку трехсила определяется скоростью изменения импульса по отношению к координатному времени, то есть dp / dt, в то время как четырехсила определяется скоростью изменения импульса по отношению к собственному времени, то есть dp / dτ .
В сплошной среде трехмерная плотность силы объединяется с плотностью мощности, образуя ковариантный 4-вектор. Пространственная часть является результатом деления силы, действующей на маленькую ячейку (в трехмерном пространстве) на объем этой ячейки. Временная составляющая равна -1/ c, умноженной на мощность, передаваемую в эту ячейку, деленную на объем ячейки. Это будет использоваться ниже в разделе, посвященном электромагнетизму.
См. также [ править ]
- Люди :
- Относительность :
- Физика :
- Математика :
- Философия :
- Парадоксы :
Примечания [ править ]
- ^ Сам Эйнштейн, в «Основах общей теории относительности», Ann. Физ. 49 (1916) пишет: «Слово «специальный» означает, что принцип ограничен случаем…». См. стр. 111 «Принципа относительности», А. Эйнштейн, Х. А. Лоренц, Х. Вейль, Х. Минковский, Дуврское переиздание перевода Метуэна и компании 1923 года.]
- ^ Уолд, Общая теория относительности, с. 60: «...специальная теория относительности утверждает, что пространство-время — это многообразие с определенной на ней плоской метрикой сигнатуры Лоренца. И наоборот, все содержание специальной теории относительности... содержится в этом утверждении..."
- ^ В пространственно-временном измерении длина движущегося твердого объекта — это пространственное расстояние между концами объекта, измеренное одновременно. В остальном кадре объекта одновременность не требуется.
- ^ Результаты эксперимента Майкельсона-Морли побудили Джорджа Фрэнсиса Фитцджеральда и Хендрика Лоренца независимо предложить явление сокращения длины . Лоренц считал, что сокращение длины представляет собой физическое сжатие атомов, составляющих объект. Он не предполагал никаких фундаментальных изменений в природе пространства и времени. [28] : 62–68
Лоренц ожидал, что сокращение длины приведет к сжимающим деформациям объекта, что должно привести к измеримым эффектам. К таким эффектам относятся оптические эффекты в прозрачных средах, такие как оптическое вращение. [стр. 11] и индукция двойного лучепреломления, [стр. 12] и индукция крутящих моментов на заряженных конденсаторах, движущихся под углом к эфиру. [стр. 12] Лоренц был озадачен такими экспериментами, как эксперимент Траутона-Нобла и экспериментами Рэлея и Брейса , которые не подтвердили его теоретические ожидания. [28] - ^ Для математической последовательности Лоренц предложил новую переменную времени, «местное время», названную так, потому что она зависела от положения движущегося тела, следуя соотношению . [стр. 13] Лоренц считал местное время не «реальным»; скорее, это представляло собой специальное изменение переменной. [29] : 51, 80
Впечатленный «самой гениальной идеей Лоренца», Пуанкаре увидел в местном времени нечто большее, чем просто математический трюк. Оно представляло собой фактическое время, которое будет показано на часах движущегося наблюдателя. С другой стороны, Пуанкаре не считал это измеренное время «истинным временем», которое могли бы показывать часы, покоящиеся в эфире. Пуанкаре не пытался переопределить понятия пространства и времени. По мнению Пуанкаре, преобразование Лоренца описывало видимые состояния поля для движущегося наблюдателя. Истинными состояниями оставались состояния, определенные по отношению к эфиру. [30] - ^ Эта концепция противоречива хотя бы потому, что, в отличие от обычных понятий расстояния , она может принимать отрицательные значения (не является положительно определенной для несовпадающих событий), а также то, что квадратное обозначение вводит в заблуждение. Этот отрицательный квадрат привел к концепции мнимого времени , которая сейчас широко не используется . Сразу видно, что негатив также является инвариантом, порожденным вариантом метрической подписи пространства-времени.
- ^ Инвариантность Δs 2 при стандартном преобразовании Лоренца аналогично инвариантности квадратов расстояний Δr 2 при вращениях в евклидовом пространстве. Хотя пространство и время имеют равные права в теории относительности, знак минус перед пространственными терминами отмечает, что пространство и время имеют существенно разный характер. Они не одинаковы. Поскольку оно трактует время иначе, чем три пространственных измерения, пространство Минковского отличается от четырехмерного евклидова пространства .
- ^ Зависимость показателя преломления предполагаемого частичного сопротивления эфира была в конечном итоге подтверждена Питером Зееманом в 1914–1915 годах, спустя много времени после того, как специальная теория относительности была принята общепринятым направлением. Используя увеличенную версию аппарата Майкельсона, подключенную непосредственно к главному водопроводу Амстердама , Зееман смог выполнить расширенные измерения, используя монохроматический свет от фиолетового (4358 Å) до красного (6870 Å). [стр. 17] [стр. 18]
- ^ Несмотря на то, что прошло много десятилетий с тех пор, как Террелл и Пенроуз опубликовали свои наблюдения, популярные статьи продолжают смешивать размеры и внешний вид. Например, Мичио Каку писал в «Космосе Эйнштейна» (WW Norton & Company, 2004, стр. 65): «...представьте, что скорость света составляет всего 20 миль в час. Если бы по улице ехала машина, она может выглядеть сжатым в направлении движения, будучи сжатым, как аккордеон, примерно до 1 дюйма в длину».
- ^ В письме Карлу Зеилигу в 1955 году Эйнштейн написал: «Ранее я уже обнаружил, что теория Максвелла не учитывает микроструктуру излучения и, следовательно, не может иметь общей достоверности», письмо Эйнштейна Карлу Зеилигу, 1955.
Первоисточники [ править ]
- ^ Jump up to: Перейти обратно: а б с д и ж г Альберт Эйнштейн (1905) « Zur Elektrodynamic bewegter Körper », Annalen der Physik 17: 891; Английский перевод Уилфрида Перретта «Об электродинамике движущихся тел» и Джорджа Баркера Джеффри (1923); Еще один английский перевод Об электродинамике движущихся тел» « Мег Над Саха (1920).
- ^ «Наука и здравый смысл», П.В. Бриджмен, The Scientific Monthly , Vol. 79, № 1 (июль 1954 г.), стр. 32–39.
- ^ Электромагнитная масса и импульс вращающегося электрона, Г. Брейт, Труды Национальной академии наук, Vol. 12, с.451, 1926 г.
- ^ Кинематика электрона с осью. Фил. Маг. 3:1-22. Л. Х. Томас.]
- ^ Jump up to: Перейти обратно: а б Эйнштейн, Автобиографические заметки, 1949.
- ^ Эйнштейн, «Фундаментальные идеи и методы теории относительности», 1920 г.
- ^ Эйнштейн, О принципе относительности и выводах, сделанных на его основе, 1907; «Принцип относительности и его последствия в современной физике», 1910; «Теория относительности», 1911 г.; Рукопись по специальной теории относительности, 1912 г.; Теория относительности, 1913; Эйнштейн, «Относительность, специальная и общая теория», 1916; Основные идеи теории относительности, 1916 г.; Что такое теория относительности?, 1919; Принцип относительности (Принстонские лекции), 1921 г.; «Физика и реальность», 1936; Теория относительности, 1949.
- ^ Яаков Фридман (2004). Физическое применение однородных шариков . Прогресс математической физики. Том. 40. стр. 1–21. ISBN 978-0-8176-3339-4 .
- ^ Дас, А. (1993) Специальная теория относительности, математическое изложение , Springer, ISBN 0-387-94042-1 .
- ^ Шутц, Дж. (1997) Независимые аксиомы пространства-времени Минковского, Addison Wesley Longman Limited, ISBN 0-582-31760-6 .
- ^ Лоренц, Х.А. (1902). «Вращение плоскости поляризации в движущихся средах» (PDF) . Институт Гюйгенса — Королевская Нидерландская академия искусств и наук (KNAW) . 4 : 669–678. Бибкод : 1901KNAB....4..669L . Проверено 15 ноября 2018 г.
- ^ Jump up to: Перейти обратно: а б Лоренц, Х.А. (1904). «Электромагнитные явления в системе, движущейся со скоростью, меньшей скорости света» (PDF) . Институт Гюйгенса — Королевская Нидерландская академия искусств и наук (KNAW) . 6 : 809–831. Бибкод : 1903KNAB....6..809L . Проверено 15 ноября 2018 г.
- ^ Лоренц, Хендрик (1895). «Исследование колебаний, возбуждаемых колеблющимися ионами» . Попытка теории электрических и оптических явлений в движущихся телах . Лейден: Э. Дж. Брилл. (подраздел § 31).
- ^ Линь, Ши-Чунь; Джаллоренци, Томас Г. (1979). «Анализ чувствительности кольцевого оптоволоконного интерферометра на эффекте Саньяка». Прикладная оптика . 18 (6): 915–931. Бибкод : 1979ApOpt..18..915L . дои : 10.1364/AO.18.000915 . ПМИД 20208844 . S2CID 5343180 .
- ^ Шоу, Р. (1962). «Парадокс сокращения длины». Американский журнал физики . 30 (1): 72. Бибкод : 1962AmJPh..30...72S . дои : 10.1119/1.1941907 . S2CID 119855914 .
- ^ Г.А. Бенфорд; DL Book и WA Ньюкомб (1970). «Тахионный антителефон». Физический обзор D . 2 (2): 263–265. Бибкод : 1970PhRvD...2..263B . дои : 10.1103/PhysRevD.2.263 . S2CID 121124132 .
- ^ Зееман, Питер (1914). «Коэффициент Френеля для света разных цветов. (Первая часть)» . Учеб. Кон. акад. Ван Ветен . 17 : 445–451. Бибкод : 1914KNAB...17..445Z .
- ^ Зееман, Питер (1915). «Коэффициент Френеля для света разных цветов. (Вторая часть)» . Учеб. Мог. акад. От знания . 18 : 398–408. Стартовый код : 1915KNAB...18..398Z .
- ^ Террелл, Джеймс (15 ноября 1959 г.). «Невидимость лоренцева сокращения». Физический обзор . 116 (4): 1041–1045. Бибкод : 1959PhRv..116.1041T . дои : 10.1103/PhysRev.116.1041 .
- ^ Пенроуз, Роджер (24 октября 2008 г.). «Видимая форма релятивистски движущейся сферы». Математические труды Кембриджского философского общества . 55 (1): 137–139. Бибкод : 1959PCPS...55..137P . дои : 10.1017/S0305004100033776 . S2CID 123023118 .
- ^ Jump up to: Перейти обратно: а б с Зависит ли инерция тела от его энергетического содержания? А. Эйнштейн, Annalen der Physik. 18 :639, 1905 г. (английский перевод У. Перретта и Дж. Б. Джеффри)
- ^ Об инерции энергии, требуемой принципом относительности , А. Эйнштейн, Annalen der Physik 23 (1907): 371–384.
- ^ Jump up to: Перейти обратно: а б с Чемпион, Фрэнк Клайв (1932). «О некоторых близких столкновениях быстрых β-частиц с электронами, сфотографированных методом разложения» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 136 (830). Издательство Королевского общества: 630–637. Бибкод : 1932RSPSA.136..630C . дои : 10.1098/rspa.1932.0108 . S2CID 123018629 .
- ^ Бальо, Жюльен (26 мая 2007 г.). «Ускорение в специальной теории относительности: что означает «равномерно ускоренное движение»?» (PDF) . Физический факультет, ENS Cachan . Проверено 22 января 2016 г.
- ^ Jump up to: Перейти обратно: а б ПАМ Дирак (1930). «Теория электронов и протонов» . Труды Королевского общества . А126 (801): 360–365. Бибкод : 1930RSPSA.126..360D . дои : 10.1098/rspa.1930.0013 . JSTOR 95359 .
- ^ CD Андерсон (1933). «Положительный электрон» . Физ. Преподобный . 43 (6): 491–494. Бибкод : 1933PhRv...43..491A . дои : 10.1103/PhysRev.43.491 .
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б с Гриффитс, Дэвид Дж. (2013). «Электродинамика и относительность». Введение в электродинамику (4-е изд.). Пирсон. Глава 12. ISBN 978-0-321-85656-2 .
- ^ Jump up to: Перейти обратно: а б с Джексон, Джон Д. (1999). «Специальная теория относительности». Классическая электродинамика (3-е изд.). John Wiley & Sons, Inc. Глава 11. ISBN 0-471-30932-Х .
- ^ Гольдштейн, Герберт (1980). «Глава 7: Специальная теория относительности в классической механике». Классическая механика (2-е изд.). Издательство Аддисон-Уэсли. ISBN 0-201-02918-9 .
- ^ Jump up to: Перейти обратно: а б Ланцос, Корнелиус (1970). «Глава IX: Релятивистская механика». Вариационные принципы механики (4-е изд.). Дуврские публикации. ISBN 978-0-486-65067-8 .
- ^ Том Робертс и Зигмар Шляйф (октябрь 2007 г.). «Какова экспериментальная основа специальной теории относительности?» . Usenet Часто задаваемые вопросы по физике . Проверено 17 сентября 2008 г.
- ^ Альберт Эйнштейн (2001). Относительность: специальная и общая теория (перепечатка перевода 1920 года под ред. Роберта В. Лоусона). Рутледж. п. 48. ИСБН 978-0-415-25384-0 .
- ^ Лекции Фейнмана по физике Том. Я Ч. 15-9: Эквивалентность массы и энергии
- ^ Шон Кэрролл, Конспект лекций по общей теории относительности, гл. 1, «Специальная теория относительности и плоское пространство-время», http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html.
- ^ Кокс, Дон (2006). Исследования в области математической физики: концепции элегантного языка (иллюстрированное издание). Springer Science & Business Media. п. 234. ИСБН 978-0-387-32793-8 . Выдержка со страницы 234
- ^ Стейн, Эндрю М. (2012). Относительность стала относительно простой (иллюстрированное издание). ОУП Оксфорд. п. 226. ИСБН 978-0-19-966286-9 . Выдержка со страницы 226
- ^ Эдвин Ф. Тейлор и Джон Арчибальд Уилер (1992). Физика пространства-времени: Введение в специальную теорию относительности . У. Х. Фриман. ISBN 978-0-7167-2327-1 .
- ^ Jump up to: Перейти обратно: а б с д и Риндлер, Вольфганг (1977). Существенная теория относительности: специальная, общая и космологическая (иллюстрированное изд.). Springer Science & Business Media. п. §1,11 с. 7. ISBN 978-3-540-07970-5 .
- ^ «Джеймс Клерк Максвелл: сила физики» . Мир физики . 01.12.2006 . Проверено 22 марта 2024 г.
- ^ «Ноябрь 1887 года: Майкельсон и Морли сообщают о своей неудаче в обнаружении светоносного эфира» . www.aps.org . Проверено 22 марта 2024 г.
- ^ Майкл Поланьи (1974) Личное знание: на пути к посткритической философии , ISBN 0-226-67288-3 , сноска, стр. 10–11: Эйнштейн сообщает через доктора Н. Бальзаса в ответ на вопрос Поланьи, что «эксперимент Майкельсона-Морли не сыграл никакой роли в основании теории». и «...теория относительности вообще не была создана для объяснения ее результатов». [1]
- ^ Jump up to: Перейти обратно: а б Йерун ван Донген (2009). «О роли эксперимента Майкельсона-Морли: Эйнштейн в Чикаго». Архив истории точных наук . 63 (6): 655–663. arXiv : 0908.1545 . Бибкод : 2009arXiv0908.1545V . дои : 10.1007/s00407-009-0050-5 . S2CID 119220040 .
- ^ Обзор таких выводов см. Лукас и Ходжсон, Пространство-время и электромагнетизм, 1990.
- ^ Эйнштейн А., Лоренц Х.А., Минковский Х. и Вейль Х. (1952). Принцип относительности: сборник оригинальных мемуаров по специальной и общей теории относительности . Публикации Courier Dover. п. 111. ИСБН 978-0-486-60081-9 .
{{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Кольер, Питер (2017). Самая непостижимая вещь: заметки к очень мягкому введению в математику относительности (3-е изд.). Непонятные книги. ISBN 9780957389465 .
- ^ Стейли, Ричард (2009), «Альберт Майкельсон, скорость света и эфирный дрейф», поколение Эйнштейна. Истоки революции относительности, Чикаго: Издательство Чикагского университета, ISBN 0-226-77057-5
- ^ Jump up to: Перейти обратно: а б с д и ж г час Дэвид Морин (2007) Введение в классическую механику , Издательство Кембриджского университета, Кембридж, глава 11, Приложение I, ISBN 1-139-46837-5 .
- ^ Миллер, диджей (2010). «Конструктивный подход к специальной теории относительности». Американский журнал физики . 78 (6): 633–638. arXiv : 0907.0902 . Бибкод : 2010AmJPh..78..633M . дои : 10.1119/1.3298908 . S2CID 20444859 .
- ^ Тейлор, Эдвин; Уиллер, Джон Арчибальд (1992). Физика пространства-времени (2-е изд.). WH Freeman & Co. ISBN 978-0-7167-2327-1 .
- ^ Каллахан, Джеймс Дж. (2011). Геометрия пространства-времени: введение в специальную и общую теорию относительности . Нью-Йорк: Спрингер. ISBN 9781441931429 .
- ^ П.Г. Бергманн (1976) Введение в теорию относительности , Дуврское издание, глава IV, стр. 36 ISBN 0-486-63282-2 .
- ^ Мермин, Н. Дэвид (1968). Пространство и время в специальной теории относительности . МакГроу-Хилл. ISBN 978-0881334203 .
- ^ Роберт Резник (1968). Введение в специальную теорию относительности . Уайли. стр. 62–63. ISBN 9780471717249 .
- ^ Jump up to: Перейти обратно: а б Миллер, Артур И. (1998). Специальная теория относительности Альберта Эйнштейна: возникновение (1905 г.) и ранняя интерпретация (1905–1911 гг.) . Мью-Йорк: Springer-Verlag. ISBN 978-0-387-94870-6 .
- ^ Бернштейн, Джереми (2006). Тайны Старика: Эйнштейн, 1905 год . Книги Коперника (отпечаток Springer Science + Business Media). ISBN 978-0387-26005-1 .
- ^ Дарригол, Оливье (2005). «Генезис теории относительности» (PDF) . Семинар Пуанкаре . 1 :1–22. Бибкод : 2006eins.book....1D . Проверено 15 ноября 2018 г.
- ^ Jump up to: Перейти обратно: а б с Риндлер, Вольфганг (1977). Существенная теория относительности (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-10090-6 .
- ^ Jump up to: Перейти обратно: а б с д Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (1966). Физика пространства-времени (1-е изд.). Сан-Франциско: WH Freeman and Company.
- ^ Эшби, Нил (2003). «Относительность в системе глобального позиционирования» . Живые обзоры в теории относительности . 6 (1): 1. Бибкод : 2003LRR.....6....1A . дои : 10.12942/lrr-2003-1 . ПМЦ 5253894 . ПМИД 28163638 .
- ^ Дэниел Клеппнер и Дэвид Коленкоу (1973). Введение в механику . МакГроу-Хилл. стр. 468–70 . ISBN 978-0-07-035048-9 .
- ^ Jump up to: Перейти обратно: а б с Французский, AP (1968). Специальная теория относительности . Нью-Йорк: WW Norton & Company. ISBN 0-393-09793-5 .
- ^ Льюис, Гилберт Ньютон; Толман, Ричард Чейз (1909). «Принцип относительности и неньютоновская механика» . Труды Американской академии искусств и наук . 44 (25): 709–726. дои : 10.2307/20022495 . JSTOR 20022495 . Проверено 22 августа 2023 г.
- ^ Jump up to: Перейти обратно: а б Кувай, Камилло (1971). «Поль Ланжейн и теория относительности» (PDF) . Японские исследования в истории науки . 10 : 113–142 . Проверено 12 июня 2023 г.
- ^ Кэссиди, Дэвид С.; Холтон, Джеральд Джеймс; Резерфорд, Флойд Джеймс (2002). Понимание физики . Спрингер-Верлаг . п. 422. ИСБН 978-0-387-98756-9 .
- ^ Катнер, Марк Лесли (2003). Астрономия, физическая перспектива . Издательство Кембриджского университета . п. 128. ИСБН 978-0-521-82196-4 .
- ^ Эллис, Джордж Ф.Р.; Уильямс, Рут М. (2000). Плоское и искривленное пространство-время (2-е изд.). Издательство Оксфордского университета . стр. 28–29. ISBN 978-0-19-850657-7 .
- ^ Фейнман, Ричард П.; Лейтон, Роберт Б.; Сэндс, Мэтью (2011). Фейнман читает лекции по физике; том I: Издание нового тысячелетия . Основные книги. п. 15-5. ISBN 978-0-465-02414-8 . Проверено 12 июня 2023 г.
- ^ Jump up to: Перейти обратно: а б Холлидей, Дэвид; Резник, Роберт (1988). Фундаментальная физика: Расширенное третье издание . Нью-Йорк: Джон Уайли и сыновья. стр. 958–959. ISBN 0-471-81995-6 .
- ^ Адамс, Стив (1997). Относительность: введение в физику пространства-времени . ЦРК Пресс . п. 54. ИСБН 978-0-7484-0621-0 .
- ^ Ланжевен, Поль (1911). «Эволюция пространства и времени» . Сциентия . 10 :31–54 . Проверено 20 июня 2023 г.
- ^ Дебс, Талал А.; Рыжий, Майкл Л.Г. (1996). «Парадокс близнецов» и условность одновременности». Американский журнал физики . 64 (4): 384–392. Бибкод : 1996AmJPh..64..384D . дои : 10.1119/1.18252 .
- ^ Толман, Ричард К. (1917). Теория относительности движения . Беркли: Издательство Калифорнийского университета. п. 54.
- ^ Такеучи, Тацу. «Конспекты лекций по специальной теории относительности - Раздел 10» . Вирджинский технологический институт . Проверено 31 октября 2018 г.
- ^ Морен, Дэвид (2017). Специальная теория относительности для начинающих энтузиастов . Независимая издательская платформа CreateSpace. стр. 90–92. ISBN 9781542323512 .
- ^ Гиббс, Филип. «Возможны ли путешествия или связь со скоростью, превышающей скорость света?» . Часто задаваемые вопросы по физике . Департамент математики Калифорнийского университета в Риверсайде . Проверено 31 октября 2018 г.
- ^ Гинзбург, Дэвид (1989). Приложения электродинамики в теоретической физике и астрофизике (иллюстрированное изд.). ЦРК Пресс. п. 206. Бибкод : 1989aetp.book.....G . ISBN 978-2-88124-719-4 . Выдержка со страницы 206
- ^ Уэсли К. Салмон (2006). Четыре десятилетия научных объяснений . Университет Питтсбурга. п. 107. ИСБН 978-0-8229-5926-7 . , раздел 3.7 стр. 107
- ^ Логини, П. (2004). «Измерение скорости света: зачем? Скорость чего?» (PDF) . Материалы Пятой Международной конференции по истории науки в естественнонаучном образовании . Архивировано из оригинала (PDF) 4 июля 2015 года . Проверено 3 июля 2015 г.
- ^ Стэчел, Дж. (2005). «Коэффициент Френеля (перетаскивания) как вызов оптике движущихся тел XIX века» . В Коксе, Эй Джей; Эйзенштадт, Дж. (ред.). Вселенная общей теории относительности . Бостон: Биркхойзер. стр. 1–13. ISBN 978-0-8176-4380-5 . Проверено 17 апреля 2012 г.
- ^ Ричард А. Молд (2001). Основная теория относительности (2-е изд.). Спрингер. п. 8. ISBN 978-0-387-95210-9 .
- ^ Зайдельманн, П. Кеннет, изд. (1992). Пояснительное приложение к Астрономическому альманаху . Ил-Вэлли, Калифорния: Университетские научные книги. п. 393. ИСБН 978-0-935702-68-2 .
- ^ Ферраро, Рафаэль; Сфорца, Дэниел М. (2005). «Логотип Европейского физического общества Араго (1810 г.): первый результат эксперимента с эфиром». Европейский журнал физики . 26 (1): 195–204. arXiv : физика/0412055 . Бибкод : 2005EJPh...26..195F . дои : 10.1088/0143-0807/26/1/020 . S2CID 119528074 .
- ^ Долан, Грэм. «Водный телескоп Эйри (1870 г.)» . Королевская обсерватория Гринвич . Проверено 20 ноября 2018 г.
- ^ Холлис, HP (1937). «Водный телескоп Эйри» . Обсерватория . 60 : 103–107. Бибкод : 1937Obs....60..103H . Проверено 20 ноября 2018 г.
- ^ Янссен, Мишель; Стэйчел, Джон (2004). «Оптика и электродинамика движущихся тел» (PDF) . В Стэчеле, Джон (ред.). Становимся критическими . Спрингер. ISBN 978-1-4020-1308-9 .
- ^ Шер, Д. (1968). «Релятивистский эффект Доплера» . Журнал Королевского астрономического общества Канады . 62 : 105–111. Бибкод : 1968JRASC..62..105S . Проверено 11 октября 2018 г.
- ^ Гилл, Т.П. (1965). Эффект Доплера . Лондон: Logos Press Limited. стр. 6–9. ОЛ 5947329М .
- ^ Фейнман, Ричард П .; Лейтон, Роберт Б .; Сэндс, Мэтью (февраль 1977 г.). «Релятивистские эффекты в радиации» . Фейнмановские лекции по физике: Том 1 . Ридинг, Массачусетс: Аддисон-Уэсли . стр. 34–7 ф. ISBN 9780201021165 . LCCN 2010938208 .
- ^ Кук, Хелен. «Релятивистское искажение» . Математический факультет Университета Британской Колумбии . Проверено 12 апреля 2017 г.
- ^ Сигнелл, Питер. «Появления на релятивистских скоростях» (PDF) . Проект ФИЗНЕТ . Университет штата Мичиган, Ист-Лансинг, Мичиган. Архивировано из оригинала (PDF) 13 апреля 2017 года . Проверено 12 апреля 2017 г.
- ^ Краус, Уте. «Мяч круглый» . Путешествие в пространстве и времени: визуализация теории относительности . Институт физики университета Хильдесхайма. Архивировано из оригинала 12 мая 2017 года . Проверено 16 апреля 2017 г.
- ^ Боас, Мэри Л. (1961). «Видимая форма крупных объектов на релятивистских скоростях». Американский журнал физики . 29 (5): 283. Бибкод : 1961AmJPh..29..283B . дои : 10.1119/1.1937751 .
- ^ Мюллер, Томас; Боблест, Себастьян (2014). «Визуальный вид каркасных объектов в специальной теории относительности». Европейский журнал физики . 35 (6): 065025. arXiv : 1410.4583 . Бибкод : 2014EJPh...35f5025M . дои : 10.1088/0143-0807/35/6/065025 . S2CID 118498333 .
- ^ Зенсус, Дж. Антон; Пирсон, Тимоти Дж. (1987). Сверхсветовые радиоисточники (1-е изд.). Кембридж, Нью-Йорк: Издательство Кембриджского университета. п. 3. ISBN 9780521345606 .
- ^ Чейз, Скотт И. «Кажущаяся сверхсветовая скорость галактик» . Оригинальный FAQ по физике Usenet . Департамент математики Калифорнийского университета в Риверсайде . Проверено 12 апреля 2017 г.
- ^ Ричмонд, Майкл. « Сверхсветовые» движения в астрономических источниках» . Физика 200 Конспект лекций . Школа физики и астрономии Рочестерского технологического института. Архивировано из оригинала 16 февраля 2017 года . Проверено 20 апреля 2017 г.
- ^ Кил, Билл. «Джетсы, сверхсветовое движение и гамма-всплески» . Галактики и Вселенная — Конспекты курса WWW . Кафедра физики и астрономии Университета Алабамы. Архивировано из оригинала 1 марта 2017 года . Проверено 29 апреля 2017 г.
- ^ Макс Джаммер (1997). Понятия массы в классической и современной физике . Публикации Courier Dover. стр. 177–178. ISBN 978-0-486-29998-3 .
- ^ Джон Дж. Стэчел (2002). Эйнштейн Б до Я. от Спрингер. п. 221. ИСБН 978-0-8176-4143-6 .
- ^ Фернфлорес, Франциско (2018). Уравнение массы-энергии Эйнштейна, том I: Ранняя история и философские основы . Нью-Йорк: Momentum Pres. ISBN 978-1-60650-857-2 .
- ^ Jump up to: Перейти обратно: а б Идема, Тимон (17 апреля 2019 г.). «Механика и относительность. Глава 14: Релятивистские столкновения» . LibreTexts Физика . Программа доступных решений для обучения Калифорнийского государственного университета . Проверено 2 января 2023 г.
- ^ Накель, Вернер (1994). «Элементарный процесс тормозного излучения». Отчеты по физике . 243 (6): 317–353. Бибкод : 1994PhR...243..317N . дои : 10.1016/0370-1573(94)00068-9 .
- ^ Халберт, ML (1972). «Обзор экспериментов по тормозному излучению нуклон-нуклон». В Остине, С.М.; Кроули, генеральный директор (ред.). Двухчастичная сила в ядрах . Бостон, Массачусетс: Спрингер.
- ^ Jump up to: Перейти обратно: а б Филип Гиббс и Дон Кокс. «Релятивистская ракета» . Проверено 30 августа 2012 г.
- ^ Специальная теория относительности показывает, что на время и пространство влияет движение. Архивировано 21 октября 2012 г. в Wayback Machine . Library.thinkquest.org. Проверено 24 апреля 2013 г.
- ^ Э.Дж. Пост (1962). Формальная структура электромагнетизма: общая ковариация и электромагнетизм . Dover Publications Inc. ISBN 978-0-486-65427-0 .
- ^ Р. Резник; Р. Айсберг (1985). Квантовая физика атомов, молекул, твердых тел, ядер и частиц (2-е изд.). Джон Уайли и сыновья. стр. 114–116 . ISBN 978-0-471-87373-0 .
- ^ Ойвинд Грён и Сигбьёрн Хервик (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии . Спрингер. стр. 195. ISBN 978-0-387-69199-2 . Отрывок со страницы 195 (с единицами измерения, где c=1)
- ^ Количество работ огромно, см. пример:
Сидни Коулман; Шелдон Л. Глэшоу (1997). «Космические лучи и нейтринные тесты специальной теории относительности». Буквы по физике Б. 405 (3–4): 249–252. arXiv : hep-ph/9703240 . Бибкод : 1997PhLB..405..249C . дои : 10.1016/S0370-2693(97)00638-2 . S2CID 17286330 .
Обзор можно найти на этой странице - ^ Джон Д. Нортон, Джон Д. (2004). «Исследования Эйнштейном ковариантной электродинамики Галилея до 1905 года» . Архив истории точных наук . 59 (1): 45–105. Бибкод : 2004AHES...59...45N . дои : 10.1007/s00407-004-0085-6 . S2CID 17459755 .
- ^ Дж. А. Уиллер; К. Миснер; К. С. Торн (1973). Гравитация . WH Freeman & Co. с. 58. ИСБН 978-0-7167-0344-0 .
- ^ Дж. Р. Форшоу; А.Г. Смит (2009). Динамика и относительность . Уайли. п. 247. ИСБН 978-0-470-01460-8 .
- ^ Р. Пенроуз (2007). Дорога к реальности . Винтажные книги. ISBN 978-0-679-77631-4 .
- ^ Жан-Бернар Зубер и Клод Ицыксон, Квантовая теория поля , стр. 5, ISBN 0-07-032071-3
- ^ Чарльз В. Миснер , Кип С. Торн и Джон А. Уилер , Гравитация , стр. 51, ISBN 0-7167-0344-0
- ^ Джордж Стерман , Введение в квантовую теорию поля , стр. 4, ISBN 0-521-31132-2
- ^ Шон М. Кэрролл (2004). Пространство-время и геометрия: введение в общую теорию относительности . Эддисон Уэсли. п. 22. ISBN 978-0-8053-8732-2 .
Дальнейшее чтение [ править ]
Тексты Эйнштейна и тексты по истории специальной теории относительности
- Эйнштейн, Альберт (1920). Теория относительности: специальная и общая теория .
- Эйнштейн, Альберт (1996). Смысл относительности . Тонкие коммуникации. ISBN 1-56731-136-9
- Логунов, Анатолий А. (2005). Анри Пуанкаре и теория относительности (пер. с русского Г. Понтокорво и В. О. Соловьева под редакцией В. А. Петрова). Наука, Москва.
Учебники [ править ]
- Чарльз Миснер , Кип Торн и Джон Арчибальд Уилер (1971) Гравитация . WH Фриман и Ко. ISBN 0-7167-0334-3
- Пост, EJ, 1997 (1962) Формальная структура электромагнетизма: общая ковариация и электромагнетизм . Дуврские публикации.
- Вольфганг Риндлер (1991). Введение в специальную теорию относительности (2-е изд.), Oxford University Press. ISBN 978-0-19-853952-0 ; ISBN 0-19-853952-5
- Харви Р. Браун (2005). Физическая относительность: структура пространства-времени с динамической точки зрения, Oxford University Press, ISBN 0-19-927583-1 ; ISBN 978-0-19-927583-0
- Кадир, Асгар (1989). Теория относительности: введение в специальную теорию . Сингапур: Мировые научные публикации . п. 128. Бибкод : 1989rist.book.....Q . ISBN 978-9971-5-0612-4 .
- Французский, AP (1968). Специальная теория относительности (Вводная физика Массачусетского технологического института) (1-е изд.). WW Нортон и компания. ISBN 978-0393097931 .
- Зильберштейн, Людвик (1914). Теория относительности .
- Лоуренс Склар (1977). Пространство, время и пространство-время . Издательство Калифорнийского университета. ISBN 978-0-520-03174-6 .
- Лоуренс Склар (1992). Философия физики . Вествью Пресс. ISBN 978-0-8133-0625-4 .
- Sergey Stepanov (2018). Relativistic World . De Gruyter. ISBN 9783110515879 .
- Тейлор, Эдвин и Джон Арчибальд Уилер (1992). Физика пространства-времени (2-е изд.). WH Фриман и Ко. ISBN 0-7167-2327-1 .
- Типлер, Пол, и Ллевеллин, Ральф (2002). Современная физика (4-е изд.). WH Фриман и Ко. ISBN 0-7167-4345-0 .
Журнальные статьи [ править ]
- Альвагер, Т.; Фарли, FJM; Кьельман, Дж.; Валлин, Л.; и др. (1964). «Проверка второго постулата специальной теории относительности в области ГэВ». Письма по физике . 12 (3): 260–262. Бибкод : 1964PhL....12..260A . дои : 10.1016/0031-9163(64)91095-9 .
- Дарригол, Оливье (2004). «Тайна связи Пуанкаре-Эйнштейна». Исида . 95 (4): 614–26. дои : 10.1086/430652 . ПМИД 16011297 . S2CID 26997100 .
- Вольф, Питер; Пети, Жерар (1997). «Спутниковое испытание специальной теории относительности с использованием системы глобального позиционирования». Физический обзор А. 56 (6): 4405–09. Бибкод : 1997PhRvA..56.4405W . дои : 10.1103/PhysRevA.56.4405 .
- Специальная стипендия теории относительности
- Риндлер, Вольфганг (2011). «Специальная теория относительности: Кинематика» . Схоларпедия . 6 (2): 8520. Бибкод : 2011SchpJ...6.8520R . doi : 10.4249/scholarpedia.8520 .
Внешние ссылки [ править ]
Оригинальные работы [ править ]
- Об электродинамике движущихся тел Оригинальная работа Эйнштейна на немецком языке «Анналы физики» , Берн , 1905 г.
- Английский перевод «К электродинамике движущихся тел» , опубликованный в книге « Принцип относительности» 1923 года .
теория относительности для широкой аудитории (математические знания не требуются Специальная )
- Einstein Light . Отмеченное наградами нетехническое введение (видеоклипы и демонстрации), подкрепленное десятками страниц дальнейших объяснений и анимаций на уровнях с математикой или без нее
- Эйнштейн, онлайн- архив. Архивировано 1 февраля 2010 г. в Wayback Machine. Введение в теорию относительности, Институт гравитационной физики Макса Планка.
- Аудио: Каин/Гей (2006) – Астрономический состав . Специальная теория относительности Эйнштейна
теории относительности (с использованием простой или более сложной Объяснение специальной математики )
- Bondi K-Calculus – Простое введение в специальную теорию относительности.
- Грега Игана Фонды .
- Заметки Хогга по специальной теории относительности. Хорошее введение в специальную теорию относительности на уровне бакалавриата с использованием математического анализа.
- Калькулятор относительности: Специальная теория относительности. Архивировано 21 марта 2013 г. на Wayback Machine . Вывод алгебраического и интегрального исчисления для E = mc. 2 .
- MathPages – Размышления об относительности Полная онлайн-книга по теории относительности с обширной библиографией.
- Специальная теория относительности. Введение в специальную теорию относительности на уровне бакалавриата.
- Относительность: специальная и общая теория в проекте «Гутенберг» , Альберт Эйнштейн
- Конспекты лекций по специальной теории относительности — это стандартное введение в специальную теорию относительности, содержащее иллюстративные пояснения, основанные на рисунках и диаграммах пространства-времени, полученных в Политехническом институте Вирджинии и Государственном университете.
- Понимание специальной теории относительности. Специальная теория относительности в доступной для понимания форме.
- «Введение в специальную теорию относительности» (1964) Роберта Каца, «введение… которое доступно любому студенту, знакомому с общей физикой и имеющему некоторое представление о математическом анализе» (130 стр.; формат pdf) .
- Конспект лекций по специальной теории относительности Дж. Д. Крессера, факультет физики Университета Маккуори.
- SpecialRelativity.net – обзор с визуализацией и минимальной математикой.
- Относительность 4-когда-либо? В занимательной форме обсуждается проблема сверхсветового движения.
Визуализация [ править ]
- Программное обеспечение специальной теории относительности для трассировки лучей, визуализирующее несколько сценариев под влиянием специальной теории относительности.
- Относительность в реальном времени. Архивировано 8 мая 2013 г. в Wayback Machine , Австралийский национальный университет. Релятивистские визуальные эффекты, наблюдаемые с помощью интерактивной программы.
- Путешествие в пространстве-времени. Разнообразные визуализации релятивистских эффектов, от релятивистского движения до черных дыр.
- Глазами Эйнштейна. Архивировано 14 мая 2013 г. в Wayback Machine , Австралийский национальный университет. Релятивистские визуальные эффекты, объясненные с помощью фильмов и изображений.
- Специальный симулятор относительности Warp Компьютерная программа, демонстрирующая эффекты путешествий со скоростью, близкой к скорости света.
- Анимационный клип на YouTube, визуализирующий преобразование Лоренца.
- Оригинальные интерактивные FLASH-анимации Джона де Пиллиса, иллюстрирующие системы Лоренца и Галилея, парадокс поезда и туннеля, парадокс близнецов, распространение волн, синхронизацию часов и т. д.
- Lightspeed Программа на основе OpenGL, разработанная для иллюстрации влияния специальной теории относительности на внешний вид движущихся объектов.
- Анимация, показывающая звезды вблизи Земли, как видно с космического корабля, быстро разгоняющегося до скорости света.
















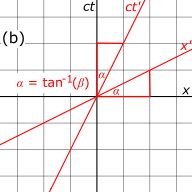












































































































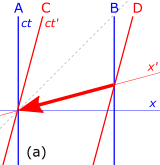












![{\displaystyle \sin \theta '= {\frac {\sin \theta }{\gamma [1+(v/c)\cos \theta ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b1d959a5aa9840f249611011e804cba5079e53)


















![{\displaystyle {\begin{aligned}E_{0}&=E_{1}+{\tfrac {1}{2}}L+{\tfrac {1}{2}}L=E_{1}+L\ \[5mu]H_{0}&=H_{1}+{\tfrac {1}{2}}L{\frac {1-(v/c)\cos {\phi }}{\sqrt {1- v^{2}/c^{2}}}}+{\tfrac {1}{2}}L{\frac {1+(v/c)\cos {\phi }}{\sqrt {1- v^{2}/c^{2}}}}=H_{1}+{\frac {L}{\sqrt {1-v^{2}/c^{2}}}}\end{aligned }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/343ffb26e1d6fe9149832c6e8b3f2ef79fecad0c)


































































