Выводы преобразований Лоренца.

Существует множество способов вывода преобразований Лоренца с использованием различных физических принципов, от уравнений Максвелла Эйнштейна до постулатов специальной теории относительности , а также математических инструментов, от элементарной алгебры и гиперболических функций до линейной алгебры и теории групп .

В этой статье представлены некоторые из наиболее простых для использования в контексте специальной теории относительности простейшего случая повышения Лоренца в стандартной конфигурации, то есть двух инерциальных систем отсчета, движущихся относительно друг друга с постоянной (равномерной) относительной скоростью, меньшей скорости света и используя декартовы координаты так, чтобы оси x и x ' были коллинеарны .

Преобразование Лоренца

Основная статья: преобразование Лоренца

В фундаментальных разделах современной физики , а именно в общей теории относительности и ее широко применимом подмножестве специальной теории относительности , а также в релятивистской квантовой механике и релятивистской квантовой теории поля , преобразование Лоренца представляет собой правило преобразования, согласно которому все четырехвекторы и тензоры, содержащие физические величины, преобразуются из одной системы отсчета в другую.

Яркими примерами таких четырехвекторов являются четыре положения и четыре импульса частицы электромагнитный , а для полей - тензор и тензор энергии-импульса . Тот факт, что эти объекты преобразуются в соответствии с преобразованием Лоренца, математически определяет их как векторы и тензоры; см. тензоре определение в .

Учитывая компоненты четырехвекторов или тензоров в некотором кадре, «правило преобразования» позволяет определить измененные компоненты тех же четырехвекторов или тензоров в другом кадре, которые можно усилить или ускорить по отношению к исходному кадру. . «Ускорение» не следует путать с пространственным перемещением , оно скорее характеризуется относительной скоростью между кадрами. Само правило трансформации зависит от относительного движения кадров. В простейшем случае двух инерциальных систем отсчета в правило преобразования входит относительная скорость между ними. Для вращающихся систем отсчета или обычных неинерциальных систем отсчета требуется больше параметров, включая относительную скорость (величину и направление), ось вращения и угол поворота.

Историческая справка

Дополнительная информация: История преобразований Лоренца.

Обычная трактовка (например, оригинальная работа Альберта Эйнштейна ) основана на инвариантности скорости света. Однако это не обязательно является отправной точкой: действительно (как описано, например, во втором томе «Курса теоретической физики» Ландау что и Лифшица ) на самом деле речь идет о локальности взаимодействий: предполагается, Влияние, которое, скажем, одна частица оказывает на другую, не может быть передано мгновенно. Следовательно, существует теоретическая максимальная скорость передачи информации, которая должна быть инвариантной, и оказывается, что эта скорость совпадает со скоростью света в вакууме. Сам Ньютон называл идею действия на расстоянии с философской точки зрения «абсурдной» и считал, что гравитация должна передаваться каким-то агентом в соответствии с определенными законами.

Майкельсон и Морли в 1887 году разработали эксперимент с использованием интерферометра и полупосеребренного зеркала, который был достаточно точным, чтобы обнаружить поток эфира . Система зеркал отражала свет обратно в интерферометр. Если бы существовал дрейф эфира , это привело бы к фазовому сдвигу и изменению помех, которые были бы обнаружены. Однако никакого фазового сдвига так и не было обнаружено. Отрицательный результат эксперимента Майкельсона-Морли подорвал концепцию эфира (или его дрейфа). В результате возникло недоумение относительно того, почему свет, очевидно, ведет себя как волна, без какой-либо заметной среды, через которую могла бы распространяться волновая активность.

В статье 1964 г. Эрик Кристофер Зееман показал, что свойства сохранения причинности , условия, которое в математическом смысле более слабое, чем инвариантность скорости света, достаточно, чтобы гарантировать, что преобразования координат являются преобразованиями Лоренца. Статья Нормана Гольдштейна показывает аналогичный результат, используя инерциальность (сохранение времениподобных линий), а не причинность .

Физические принципы

Эйнштейн основал свою специальную теорию относительности на двух фундаментальных постулатах . Во-первых, все физические законы одинаковы для всех инерциальных систем отсчета, независимо от их относительного состояния движения; и во-вторых, скорость света в свободном пространстве одинакова во всех инерциальных системах отсчета, опять же, независимо от относительной скорости каждой системы отсчета. Преобразование Лоренца по сути является прямым следствием этого второго постулата.

Второй постулат

Предположим второй постулат специальной теории относительности, утверждающий постоянство скорости света независимо от системы отсчета, и рассмотрим совокупность систем отсчета, движущихся относительно друг друга с постоянной скоростью, то есть инерциальных систем , каждая из которых наделена своим собственным набором декартовых координаты, обозначающие точки, т.е. события пространства-времени. Чтобы выразить неизменность скорости света в математической форме, зафиксируйте два события в пространстве-времени, которые должны быть записаны в каждой системе отсчета. Пусть первое событие — это излучение светового сигнала, а второе — его поглощение.

Выберите любой опорный кадр в коллекции. В его координатах первому событию будут присвоены координаты $x_{1},y_{1},z_{1},ct_{1}$, и второй $x_{2},y_{2},z_{2},ct_{2}$. Пространственное расстояние между излучением и поглощением равно ${\textstyle {\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}}$, но это также расстояние $c(t_{2}-t_{1})$ пройденный сигналом. Поэтому можно составить уравнение

$$c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}-(y_{2}-y_{1})^{2}-(z_{2}-z_{1})^{2}=0.$$

Любая другая система координат будет записывать в своих собственных координатах одно и то же уравнение. Это непосредственное математическое следствие неизменности скорости света. Величина слева называется пространственно-временным интервалом . Интервал для событий, разделенных световыми сигналами, один и тот же (нулевой) во всех системах отсчета и поэтому называется инвариантным .

Инвариантность интервала

Чтобы преобразование Лоренца имело физический смысл, реализованный природой, крайне важно, чтобы интервал был инвариантной мерой для любых двух событий, а не только для тех, которые разделены световыми сигналами. Чтобы установить это, рассмотрим бесконечно малый интервал:

$$ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2},$$

как записано в системе $K$. Позволять $K'$ быть другой системой, определяющей интервал $ds'^{2}$ к одним и тем же двум бесконечно разделенным событиям. Поскольку если $ds^{2}=0$, то и в любой другой системе интервал будет равен нулю (второй постулат), а так как $ds^{2}$ и $ds'^{2}$ являются бесконечно малыми одного порядка, они должны быть пропорциональны друг другу,

$$ds^{2}=ads'^{2}.$$

О том, что может $a$ зависеть? Это может не зависеть от положения двух событий в пространстве-времени, поскольку это нарушило бы постулируемую однородность пространства-времени . Это может зависеть от относительной скорости $V'$ между $K$ и $K'$, но только от скорости, а не от направления, поскольку последнее нарушило бы изотропию пространства .

Теперь введем системы $K_{1}$ и $K_{2}$,

$$ds^{2}=a(V_{1})ds_{1}^{2},\quad ds^{2}=a(V_{2})ds_{2}^{2},\quad ds_{1}^{2}=a(V_{12})ds_{2}^{2}.$$

Из этого следует,

$${\frac {a(V_{2})}{a(V_{1})}}=a(V_{12}).$$

Теперь можно заметить, что в правой части $V_{12}$ зависеть от обоих $V_{1}$ и $V_{2}$; а также от угла между векторами ${\textbf {V}}_{1}$ и ${\textbf {V}}_{2}$. Однако можно заметить также, что левая часть не зависит от этого угла. Таким образом, единственный способ сохранить справедливость уравнения — это если функция $a(V)$ является константой. Далее, по тому же уравнению эта константа равна единице. Таким образом,

$$ds^{2}=ds'^{2}$$

для всех систем $K'$. Поскольку это справедливо для всех бесконечно малых интервалов, это справедливо для всех интервалов.

Большинство, если не все, выводов преобразований Лоренца принимают это как должное. В этих выводах они используют только постоянство скорости света (инвариантность отдельных светоподобных событий). Этот результат гарантирует, что преобразование Лоренца является правильным преобразованием.

Строгое утверждение и доказательство пропорциональности ds ² и дс ' ²

Теорема: Позволять $n,p\geq 1$ быть целыми числами, $d:=n+p$ и $V$ векторное пространство над $\mathbb {R}$ размера ​ $d$. Позволять $h$ быть неопределенным внутренним продуктом на $V$ с подписи типом $(n,p)$. Предполагать $g$ является симметричной билинейной формой на $V$ такой, что нулевое множество ассоциированной квадратичной формы $h$ содержится в том, что $g$ (т.е. предположим, что для каждого $v\in V$, если $h(v,v)=0$ затем $g(v,v)=0$). Тогда существует константа $C\in \mathbb {R}$ такой, что $g=Ch$. Более того, если мы предположим $n\neq p$ и это $g$ также имеет тип подписи $(n,p)$, тогда мы имеем $C>0$.

Замечания.

• В разделе выше термин «бесконечно малый» по отношению к $ds^{2}$ на самом деле относится (поточечно) к квадратичной форме над четырехмерным вещественным векторным пространством (а именно, касательным пространством в точке пространственно-временного многообразия). Приведенный выше аргумент почти дословно скопирован у Ландау и Лифшица, где пропорциональность $ds^{2}$ и $ds'^{2}$ просто констатируется как «очевидный» факт, хотя это утверждение не сформулировано математически точно и не доказано. Это неочевидный математический факт, который необходимо обосновать; к счастью, доказательство относительно простое и сводится к основным алгебраическим наблюдениям и манипуляциям.
• Вышеизложенные предположения о $h$ означает следующее: $h:V\times V\to \mathbb {R}$ — билинейная форма , симметричная и невырожденная , такая, что существует упорядоченный базис $\{v_{1},\dots ,v_{n},v_{n+1},\dots ,v_{d}\}$ из $V$ для чего
  $$h(v_{a},v_{b})={\begin{cases}-1&{\text{if }}a=b,{\text{where }}a,b\in \{1,\dots ,n\}\\1&{\text{if }}a=b,{\text{where }}a,b\in \{n+1,\dots ,d\}\\0&{\text{ otherwise}}\end{cases}}$$
  Эквивалентный способ сказать это так: $h$ имеет матричное представление ${\begin{pmatrix}-I_{n}&0\\0&I_{p}\end{pmatrix}}$ относительно заказанного базиса $\{v_{1},\dots ,v_{d}\}$.
• Если рассмотреть частный случай, когда $n=1,p=3$ тогда мы имеем дело с ситуацией лоренцевой сигнатуры в 4-х измерениях, на которой основана теория относительности (или можно было бы принять противоположное соглашение с общим знаком минус; но это явно не влияет на истинность теоремы) . Кроме того, в этом случае, если мы предположим $g$ и $h$ оба имеют квадратичные формы с одним и тем же нулевым набором (в физической терминологии мы говорим, что $g$ и $h$ порождают тот же световой конус), то теорема говорит нам, что существует постоянная $C>0$ такой, что $g=Ch$. По модулю некоторых различий в обозначениях именно это и использовалось в разделе выше .

Доказательство теоремы.

Закрепить основу $\{v_{1},\dots ,v_{d}\}$ из $V$ относительно которого $h$ имеет матричное представление $[h]={\begin{pmatrix}-I_{n}&0\\0&I_{p}\end{pmatrix}}$. Дело в том, что векторное пространство $V$ можно разложитьв подпространства $V^{-}$ (продолжительность первого $n$ базисные векторы) и $V^{+}$ (затем промежуток другого $p$ базисные векторы) такие, что каждый вектор в $V$ можно записать однозначно как $v+w$ для $v\in V^{-}$ и $w\in V^{+}$; более того $h(v,v)\leq 0$, $h(w,w)\geq 0$ и $h(v,w)=0$. Итак (по билинейности)

$$h(v+w,v+w)=h(v,v)+h(w,w)$$

Поскольку первое слагаемое справа неположительное, а второе неотрицательное, для любого $v\in V^{-}$и $w\in V^{+}$, мы можем найти скаляр $\alpha$ такой, что $h(v+\alpha w,v+\alpha w)=0$.

Отныне всегда учитывайте $v\in V^{-}$и $w\in V^{+}$. По билинейности

$${\begin{aligned}g(v+w,v+w)&=g(v,v)+g(w,w)+2g(v,w)\\g(v-w,v-w)&=g(v,v)+g(w,w)-2g(v,w)\end{aligned}}$$

Если $h(v+w,v+w)=0$, тогда также $h(v-w,v-w)=0$ и то же самое верно для $g$ (поскольку нулевой набор $h$ содержится в том, что $g$). В этом случае вычитание двух приведенных выше выражений (и деление на 4) дает

$$0=g(v,w)$$

Как указано выше, для каждого $v\in V^{-}$и $w\in V^{+}$, есть скаляр $\alpha$ такой, что $h(v+\alpha w,v+\alpha w)=0$, так $g(v,\alpha w)=0$, что под билинейностью означает $g(v,w)=0$.

Теперь рассмотрим ненулевое $v,v'\in V^{-}$ такой, что $h(v,v)=h(v',v')$. Мы можем найти $w\in V^{+}$ такой, что $0=h(v+w,v+w)=h(v,v)+h(w,w)=h(v'+w,v'+w)$. Согласно выражениям, приведенным выше,

$$g(v,v)=-g(w,w)=g(v',v')$$

Аналогично, для $w,w'\in V^{+}$, можно показать, что если $h(w,w)=h(w',w')$, тогда также $g(w,w)=g(w',w')$. Таким образом, это справедливо для всех векторов в $V$.

Для $u,u'\in V$, если $g(u,u)=Ch(u,u)\neq 0$, $g(u',u')=C'h(u',u')\neq 0$ для некоторых $C,C'\in \mathbb {R}$, мы можем (масштабируя одно из при необходимости) предположить $h(u,u)=h(u',u')$, что, как указано выше, означает, что $C=C'$. Так $g=Ch$.

Наконец, если мы предположим, что $g,h$ оба имеют типы подписи $(n,p)$ и $n\neq p$ затем $C>0$ (мы не можем иметь $C=0$ потому что это будет означать $g=0$, что невозможно, поскольку наличие типа подписи $(n,p)$ означает, что это ненулевая билинейная форма. Кроме того, если $C<0$, то это означает $g$ имеет $n$ положительные диагональные элементы и $p$ отрицательные диагональные записи; то есть это подпись $(p,n)\neq (n,p)$, поскольку мы предположили $n\neq p$, так что это тоже невозможно. Это оставляет нам $C>0$ как единственный вариант). Это завершает доказательство теоремы.

Стандартная конфигурация

Пространственно-временные координаты события, измеренные каждым наблюдателем в своей инерциальной системе отсчета (в стандартной конфигурации), показаны в облачках с текстом.
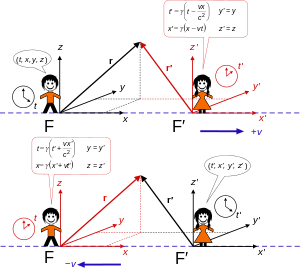
Вверху: кадр F ′ движется со скоростью v вдоль оси x кадра F .
Внизу: кадр F движется со скоростью − v вдоль оси x ′ кадра F ′.

Инвариантный интервал можно рассматривать как неположительно определенную функцию расстояния в пространстве-времени. Набор искомых преобразований должен оставить это расстояние неизменным. Из-за декартовой природы системы координат системы отсчета можно сделать вывод, что, как и в евклидовом случае, возможные преобразования состоят из сдвигов и вращений, где для термина «вращение» следует использовать несколько более широкое значение.

Интервал совершенно тривиально инвариантен относительно трансляции. Для вращения есть четыре координаты. Следовательно, имеется шесть плоскостей вращения. Три из них — вращения в пространственных плоскостях. Интервал инвариантен и относительно обычных вращений.

Осталось найти в трех оставшихся координатных плоскостях такой «поворот», который оставит интервал инвариантным. Эквивалентно, найти способ назначить координаты так, чтобы они совпадали с координатами, соответствующими движущемуся кадру.

Общая задача состоит в том, чтобы найти такое преобразование, чтобы

$${\begin{aligned}&c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}-(y_{2}-y_{1})^{2}-(z_{2}-z_{1})^{2}\\={}&c^{2}(t_{2}'-t_{1}')^{2}-(x_{2}'-x_{1}')^{2}-(y_{2}'-y_{1}')^{2}-(z_{2}'-z_{1}')^{2}.\end{aligned}}$$

Для решения общей задачи можно воспользоваться знаниями об инвариантности интервала трансляций и обычных вращений, полагая, не ограничивая общности, что рамки F и F ' выровнены таким образом, что все их оси координат встречаются в точке t = t ' = 0 , и что оси x и x ' постоянно выровнены, а система F ' имеет скорость V вдоль положительной x оси . . Назовите это стандартной конфигурацией . Это сводит общую задачу к нахождению такого преобразования, что

$$c^{2}(t_{2}-t_{1})^{2}-(x_{2}-x_{1})^{2}=c^{2}(t_{2}'-t_{1}')^{2}-(x_{2}'-x_{1}')^{2}.$$

Стандартная конфигурация используется в большинстве примеров ниже. Линейное задачи решение более простой

$$(ct)^{2}-x^{2}=(ct')^{2}-x'^{2}$$

решает более общую проблему, поскольку разности координат преобразуются таким же образом. При рассмотрении этой более простой проблемы в литературе часто предполагается или каким-либо образом аргументируется линейность. Если решение более простой задачи не является линейным, то оно не решает исходную задачу из-за появления перекрестных членов при расширении квадратов.

Решения

Как уже упоминалось, общая проблема решается путем перемещения в пространстве-времени. Они не кажутся решением более простой поставленной проблемы, в отличие от ускорений (а иногда и вращений в зависимости от угла атаки). Еще больше решений существует, если настаивать только на инвариантности интервала для светоподобных разделенных событий. Это нелинейные конформные преобразования («сохраняющие угол»). У одного есть

Преобразования Лоренца ⊂ Преобразования Пуанкаре ⊂ преобразования конформной группы .

Некоторые уравнения физики конформно-инвариантны, например, уравнения Максвелла в пространстве без источников, но не все. Актуальность конформных преобразований в пространстве-времени в настоящее время неизвестна, но конформная группа в двух измерениях весьма актуальна в конформной теории поля и статистической механике . Таким образом, постулаты специальной теории относительности выделяют именно группу Пуанкаре. Именно наличие усилений Лоренца (для которых сложение скоростей отличается от простого сложения векторов, которое допускает скорости, превышающие скорость света) в отличие от обычных ускорений, которое отделяет его от группы Галилея теории относительности Галилея . Пространственные вращения, пространственные и временные инверсии и трансляции присутствуют в обеих группах и имеют одинаковые последствия в обеих теориях (законы сохранения импульса, энергии и момента импульса). Не все общепринятые теории соблюдают симметрию при инверсиях.

Использование геометрии пространства-времени

Решение Ландау и Лифшица

Эти три формулы гиперболических функций (H1–H3) указаны ниже:

1. $\cosh ^{2}\Psi -\sinh ^{2}\Psi =1,$
2. $\sinh \Psi ={\frac {\tanh \Psi }{\sqrt {1-\tanh ^{2}\Psi }}},$
3. $\cosh \Psi ={\frac {1}{\sqrt {1-\tanh ^{2}\Psi }}},$

Задача, поставленная в стандартной конфигурации для ускорения в x направлении , где координаты со штрихом относятся к движущейся системе, решается путем нахождения линейного решения более простой задачи.

$$(ct)^{2}-x^{2}=(ct')^{2}-x'^{2}.$$

Наиболее общее решение, как можно проверить прямой заменой с использованием (H1),

$x=x'\cosh \Psi +ct'\sinh \Psi ,\quad ct=x'\sinh \Psi +ct'\cosh \Psi .$ ( 1 )

Чтобы определить роль Ψ в физической ситуации, запишите прогресс начала координат F ′ , т.е. x ′ = 0, x = vt . Уравнения становятся (используя сначала x ′ = 0 ),

$$x=ct'\sinh \Psi ,\quad ct=ct'\cosh \Psi .$$

Теперь разделите:

$${\frac {x}{ct}}=\tanh \Psi ={\frac {v}{c}}\Rightarrow \quad \sinh \Psi ={\frac {\frac {v}{c}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad \cosh \Psi ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$$

где x = vt использовалось на первом этапе, (H2) и (H3) на втором, что при повторном подключении ( 1 ) дает

$$x={\frac {x'+vt'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\quad t={\frac {t'+{\frac {v}{c^{2}}}x'}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$$

или, используя обычные сокращения,

$x=\gamma (x'+vt'),\,\,t=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right),\quad x'=\gamma (x-vt),\,\,t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right).$

Этот расчет повторяется более подробно в разделе «Гиперболическое вращение» .

Гиперболическое вращение

Основная статья: Гиперболическое вращение

Преобразования Лоренца также могут быть получены путем простого применения постулатов специальной теории относительности и использования гиперболических тождеств .

Постулаты относительности

Начнем с уравнений сферического волнового фронта светового импульса с центром в начале координат:

$$(ct)^{2}-(x^{2}+y^{2}+z^{2})=(ct')^{2}-(x'^{2}+y'^{2}+z'^{2})=0$$

которые принимают одну и ту же форму в обеих системах из-за постулатов специальной теории относительности. Далее рассмотрим относительное движение вдоль осей x каждого кадра в стандартной конфигурации, описанной выше, так что y = y ′, z = z ′, что упрощается до

$$(ct)^{2}-x^{2}=(ct')^{2}-x'^{2}$$

Линейность

Теперь предположим, что преобразования принимают линейный вид:

$${\begin{aligned}x'&=Ax+Bct\\ct'&=Cx+Dct\end{aligned}}$$

где A , B , C , D. нужно найти Если бы они были нелинейными, они не принимали бы одинаковую форму для всех наблюдателей, поскольку фиктивные силы (следовательно, ускорения) возникали бы в одной системе отсчета, даже если бы скорость была постоянной в другой, что несовместимо с преобразованиями инерциальной системы отсчета.

Подстановка в предыдущий результат:

$$(ct)^{2}-x^{2}=[(Cx)^{2}+(Dct)^{2}+2CDcxt]-[(Ax)^{2}+(Bct)^{2}+2ABcxt]$$

и сравнивая коэффициенты при x ² , т ² , хт :

$${\begin{aligned}-1=C^{2}-A^{2}&\Rightarrow &A^{2}-C^{2}=1\\c^{2}=(Dc)^{2}-(Bc)^{2}&\Rightarrow &D^{2}-B^{2}=1\\2CDc-2ABc=0&\Rightarrow &AB=CD\end{aligned}}$$

Гиперболическое вращение

Уравнения предполагают гиперболическое тождество $\cosh ^{2}\phi -\sinh ^{2}\phi =1.$

Введение быстроты параметра φ в виде гиперболического угла позволяет последовательно провести идентификацию.

$$A=D=\cosh \phi \,,\quad C=B=-\sinh \phi$$

где знаки после квадратных корней выбраны так, чтобы x и t увеличивались. Гиперболические преобразования были решены для:

$${\begin{aligned}x'&=x\cosh \phi -ct\sinh \phi \\ct'&=-x\sinh \phi +ct\cosh \phi \end{aligned}}$$

Если бы знаки были выбраны по-другому, координаты положения и времени необходимо было бы заменить на – x и/или – t, чтобы x и t увеличивались, а не уменьшались.

Чтобы выяснить, как φ связана с относительной скоростью, в стандартной конфигурации начало координат со штрихом x ′ = 0 измеряется в системе без штриха как x = vt (или эквивалентный и противоположный путь; начало координат без штриха). равен x = 0 , а в штрихованной системе координат он находится в точке x ′ = − vt ):

$$0=vt\cosh \phi -ct\sinh \phi \,\Rightarrow \,\tanh \phi ={\frac {v}{c}}=\beta$$

и гиперболические тождества $\sinh \Psi ={\frac {\tanh \Psi }{\sqrt {1-\tanh ^{2}\Psi }}},\,\cosh \Psi ={\frac {1}{\sqrt {1-\tanh ^{2}\Psi }}}$ приводит к соотношениям между β , γ и φ ,

$$\cosh \phi =\gamma ,\,\quad \sinh \phi =\beta \gamma \,.$$

Из физических принципов

Задача обычно ограничивается двумя измерениями за счет использования скорости вдоль оси x , при которой координаты y и z не пересекаются, как описано выше в стандартной конфигурации .

времени и

Уравнения преобразования могут быть получены из замедления времени и сокращения длины , которые, в свою очередь, могут быть получены из первых принципов. Поскольку O и O' представляют собой пространственные начала кадров F и F' , а также некоторое событие M , связь между векторами положения (которые здесь сводятся к ориентированным сегментам OM , OO' и O'M ) в обоих кадрах определяется выражением :

ОМ = ОО' + О'М .

Используя координаты ( x , t ) в F и ( x ', t ') в F' для события M, в кадре F сегментами являются OM = x , OO' = vt и O'M = x' / γ (поскольку x ’ — это O’M , измеренное в F’ ):

$$x=vt+x'/\gamma .$$

Аналогично, в кадре F' сегментами являются OM = x / γ (поскольку x — это OM , измеренный в F ), OO' = vt' и O'M = x' :

$$x/\gamma =vt'+x'.$$

Переставив первое уравнение, получим

$$x'=\gamma (x-vt),$$

что является пространственной частью преобразования Лоренца. Второе соотношение дает

$$x=\gamma (x'+vt'),$$

что является инверсией пространственной части. Исключение x ' между двумя уравнениями пространственной части дает

$$t'=\gamma t+{\frac {\left(1-{\gamma ^{2}}\right)x}{\gamma v}}.$$

что, если $\gamma ^{2}={\frac {1}{1-v^{2}/c^{2}}}$, упрощается до:

$$t'=\gamma (t-vx/c^{2}),$$

что является временной частью преобразования, обратное которому находится путем аналогичного исключения x :

$$t=\gamma (t'+vx'/c^{2}).$$

Сферические волновые фронты света

Следующее похоже на мнение Эйнштейна. Как и в преобразовании Галилея , преобразование Лоренца является линейным, поскольку относительная скорость систем отсчета постоянна как вектор; в противном случае силы инерции возникли бы . Их называют инерциальными или галилеевыми системами отсчета. Согласно теории относительности, ни одна галилеева система отсчета не является привилегированной. Другое условие состоит в том, что скорость света не должна зависеть от системы отсчета, практически от скорости источника света.

Рассмотрим две инерциальные системы отсчета O и O ′, предполагая, что O находится в покое, а O ′ движется со скоростью v относительно O в положительном направлении x . Происхождение O и O ' изначально совпадает друг с другом. Световой сигнал излучается из общего источника и распространяется как сферический волновой фронт. Рассмотрим точку P на сферическом волновом фронте на расстоянии r и r ′ от начала координат O и O ′ соответственно. Согласно второму постулату специальной теории относительности скорость света одинакова в обеих системах отсчета, поэтому для точки P :

$${\begin{aligned}r&=ct\\r'&=ct'.\end{aligned}}$$

Уравнение сферы в системе О имеет вид

$$x^{2}+y^{2}+z^{2}=r^{2}.$$

Для сферического волнового фронта , который становится

$$x^{2}+y^{2}+z^{2}=(ct)^{2}.$$

Аналогично, уравнение сферы в системе отсчета O ′ имеет вид

$$x'^{2}+y'^{2}+z'^{2}=r'^{2},$$

поэтому сферический волновой фронт удовлетворяет

$$x'^{2}+y'^{2}+z'^{2}=(ct')^{2}.$$

Начало координат O ' движется вдоль оси x . Поэтому,

$${\begin{aligned}y'&=y\\z'&=z.\end{aligned}}$$

x' должен меняться линейно в зависимости от x и t . Поэтому преобразование имеет вид

$$x'=\gamma x+\sigma t.$$

Для начала O ′ x′ и x определяются выражениями

$${\begin{aligned}x'&=0\\x&=vt,\end{aligned}}$$

итак, для всех t ,

$$0=\gamma vt+\sigma t$$

и таким образом

$$\sigma =-\gamma v.$$

Это упрощает преобразование в

$$x'=\gamma \left(x-vt\right)$$

где γ необходимо определить. В этот момент γ не обязательно является константой, но требуется уменьшить ее до 1 при v ≪ c .

Обратное преобразование такое же, за исключением того, что знак v меняется на противоположный:

$$x=\gamma \left(x'+vt'\right).$$

Два приведенных выше уравнения определяют связь между t и t ' как:

$$x=\gamma \left[\gamma \left(x-vt\right)+vt'\right]$$

или

$$t'=\gamma t+{\frac {\left(1-{\gamma ^{2}}\right)x}{\gamma v}}.$$

Заменяя x' , y' , z' и t' в уравнении сферического волнового фронта в системе O ',

$$x'^{2}+y'^{2}+z'^{2}=(ct')^{2},$$

с их выражениями в терминах x , y , z и t дает:

$${\gamma ^{2}}\left(x-vt\right)^{2}+y^{2}+z^{2}=c^{2}\left[\gamma t+{\frac {\left(1-{\gamma ^{2}}\right)x}{\gamma v}}\right]^{2}$$

и, следовательно,

$$\gamma ^{2}x^{2}+\gamma ^{2}v^{2}t^{2}-2\gamma ^{2}vtx+y^{2}+z^{2}=c^{2}{\gamma ^{2}}t^{2}+{\frac {\left(1-{\gamma ^{2}}\right)^{2}c^{2}x^{2}}{{\gamma ^{2}}v^{2}}}+2{\frac {\left(1-{\gamma ^{2}}\right)txc^{2}}{v}}$$

что подразумевает,

$$\left[{\gamma ^{2}}-{\frac {\left(1-{\gamma ^{2}}\right)^{2}c^{2}}{{\gamma ^{2}}v^{2}}}\right]x^{2}-2{\gamma ^{2}}vtx+y^{2}+z^{2}=\left(c^{2}{\gamma ^{2}}-v^{2}{\gamma ^{2}}\right)t^{2}+2{\frac {\left[1-{\gamma ^{2}}\right]txc^{2}}{v}}$$

или

$$\left[{\gamma ^{2}}-{\frac {\left(1-{\gamma ^{2}}\right)^{2}c^{2}}{{\gamma ^{2}}v^{2}}}\right]x^{2}-\left[2{\gamma ^{2}}v+2{\frac {\left(1-{\gamma ^{2}}\right)c^{2}}{v}}\right]tx+y^{2}+z^{2}=\left[c^{2}{\gamma ^{2}}-v^{2}{\gamma ^{2}}\right]t^{2}$$

Сравнивая коэффициент t ² в приведенном выше уравнении с коэффициентом t ² в уравнении сферического волнового фронта для кадра O получается:

$$c^{2}{\gamma ^{2}}-v^{2}{\gamma ^{2}}=c^{2}$$

Эквивалентные выражения для γ можно получить, сопоставив x ² коэффициенты или установку коэффициента tx на ноль. Перестановка:

$${\gamma ^{2}}={\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}$$

или, выбрав положительный корень, чтобы гарантировать, что оси x и x 'и оси времени указывают в одном направлении,

$${\gamma }={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$$

который называется фактором Лоренца . Это производит преобразование Лоренца из приведенного выше выражения. Это дано

$${\begin{aligned}x'&=\gamma \left(x-vt\right)\\t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\y'&=y\\z'&=z\end{aligned}}$$

Преобразование Лоренца — не единственное преобразование, оставляющее инвариантной форму сферических волн, поскольку существует более широкий набор преобразований сферических волн в контексте конформной геометрии , оставляющих инвариантным выражение $\lambda \left(\delta x^{2}+\delta y^{2}+\delta z^{2}-c^{2}\delta t^{2}\right)$. Однако конформные преобразования, изменяющие масштаб, не могут быть использованы для симметричного описания всех законов природы, включая механику , тогда как преобразования Лоренца (единственные, подразумевающие $\lambda =1$) представляют собой симметрию всех законов природы и сводятся к преобразованиям Галилея при $v\ll c$.

Теория относительности Галилея и Эйнштейна

Галилеевы системы отсчета

В классической кинематике полное смещение x в системе отсчета R представляет собой сумму относительного смещения x 'в системе отсчета R' и расстояния между двумя началами координат x - x '. Если v — относительная скорость R' относительно R, преобразование имеет вид: x = x ′ + vt или x ′ = x − vt . Эта зависимость линейна для постоянной v , то есть когда R и R ′ являются системами отсчета Галилея.

В теории относительности Эйнштейна главное отличие от теории относительности Галилея состоит в том, что координаты пространства и времени переплетены, причем в разных инерциальных системах отсчета t ≠ t ′.

Поскольку пространство предполагается однородным, преобразование должно быть линейным. Наиболее общая линейная зависимость получается с четырьмя постоянными коэффициентами: A , B , γ и b :

$$x'=\gamma x+bt$$

$$t'=Ax+Bt.$$

Линейное преобразование становится преобразованием Галилея, когда γ = B = 1, b = − v и A = 0.

Объект, находящийся в состоянии покоя в системе R' в позиции x ' = 0, движется с постоянной скоростью v в системе R'. Следовательно, преобразование должно дать x ′ = 0, если x = vt . Следовательно, b = − γv и первое уравнение записывается как

$$x'=\gamma \left(x-vt\right).$$

Использование принципа относительности

Согласно принципу относительности, не существует привилегированной системы отсчета Галилея: поэтому обратное преобразование положения из системы R ′ в систему R должно иметь ту же форму, что и исходная, но со скоростью в противоположном направлении, заменяя v с -v :

$$x=\gamma \left(x'-(-v)t'\right),$$

и таким образом

$$x=\gamma \left(x'+vt'\right).$$

Определение констант первого уравнения

Поскольку скорость света одинакова во всех системах отсчета, для случая светового сигнала преобразование должно гарантировать, что t = x / c , когда t ′ = x ′/ c .

Замена t и t ′ в предыдущих уравнениях дает:

$$x'=\gamma \left(1-v/c\right)x,$$

$$x=\gamma \left(1+v/c\right)x'.$$

Умножение этих двух уравнений дает:

$$xx'=\gamma ^{2}\left(1-v^{2}/c^{2}\right)xx'.$$

В любой момент после t = t ′ = 0 xx ′ не равно нулю, поэтому деление обеих частей уравнения на xx ′ приводит к

$$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},$$

который называется «фактор Лоренца».

Когда требуется, чтобы уравнения преобразования удовлетворяли уравнениям светового сигнала в форме x = ct и x ′ = ct ′, путем замены значений x и x' тот же метод дает то же выражение для фактора Лоренца.

Определение констант второго уравнения

Уравнение преобразования для времени можно легко получить, рассмотрев частный случай светового сигнала, снова удовлетворяющего x = ct и x ′ = ct ′ , путем подстановки почленно в полученное ранее уравнение для пространственной координаты

$$x'=\gamma (x-vt),\,$$

предоставление

$$ct'=\gamma \left(ct-{\frac {v}{c}}x\right),$$

так что

$$t'=\gamma \left(t-{\frac {v}{c^{2}}}x\right),$$

который при отождествлении с

$$t'=Ax+Bt,\,$$

определяет коэффициенты преобразования A и B как

$$A=-\gamma v/c^{2},\,$$

$$B=\gamma .\,$$

Итак, A и B — уникальные постоянные коэффициенты, необходимые для сохранения постоянства скорости света в штрихованной системе координат.

Эйнштейна

В своей популярной книге Эйнштейн вывел преобразование Лоренца, утверждая, что должны существовать две ненулевые константы связи λ и µ такие, что

$${\begin{cases}x'-ct'=\lambda \left(x-ct\right)\\x'+ct'=\mu \left(x+ct\right)\,\end{cases}}$$

которые соответствуют свету, распространяющемуся вдоль положительной и отрицательной оси X соответственно.Для света x = ct тогда и только тогда, когда x ′ = ct ′ . Сложение и вычитание двух уравнений и определение

$${\begin{cases}\gamma =\left(\lambda +\mu \right)/2\\b=\left(\lambda -\mu \right)/2,\,\end{cases}}$$

дает

$${\begin{cases}x'=\gamma x-bct\\ct'=\gamma ct-bx.\,\end{cases}}$$

Подставляя x ′ = 0, соответствующее x = vt, и отмечая, что относительная скорость равна v = bc / γ , это дает

$${\begin{cases}x'=\gamma \left(x-vt\right)\\t'=\gamma \left(t-{\frac {v}{c^{2}}}x\right)\,\end{cases}}$$

Константу γ можно оценить, потребовав c ² т ² − х ² = с ² т ' ² - х ′ ² согласно стандартной конфигурации .

Использование

Из групповых постулатов

Ниже приводится классический вывод (см., например, [1] и ссылки в нем), основанный на постулатах группы и изотропии пространства.

Координатные преобразования как группа

Преобразования координат между инерциальными системами отсчета образуют группу (называемую собственной группой Лоренца ), причем групповая операция представляет собой композицию преобразований (выполняющих одно преобразование за другим). Действительно, четыре аксиомы группы выполняются:

1. Заключение : композиция двух преобразований является преобразованием: рассмотрим композицию преобразований из инерциальной системы отсчета К в инерциальную систему отсчета К ', (обозначаем как К → К '), а затем из К ' в инерциальную систему отсчета К ", [ К ′ → K ”], существует преобразование, [ K → K ′] [ K ′ → K ”], непосредственно из инерциальной системы отсчета K в инерциальную систему отсчета K ”.
2. Ассоциативность : преобразования ([ K → K ′] [ K ′ → K "]) [ K " → K "′] и [ K → K ′] ([ K ′ → K "] [ K " → К "'] ) идентичны.
3. Элемент идентичности : существует элемент идентичности, K → K. преобразование
4. Обратный элемент : для любого преобразования K → K ′ существует обратное преобразование K ′ → K .

Матрицы преобразований, соответствующие аксиомам группы

Рассмотрим две инерциальные системы отсчета K и K ′, причем последняя движется со скоростью v относительно первой. Путем вращений и сдвигов мы можем выбрать оси x и x ′ вдоль вектора относительной скорости, а также добиться того, чтобы события ( t , x ) = (0,0) и ( t ′, x ′) = (0,0) совпадали. Поскольку увеличение скорости происходит вдоль осей x (и x ′ ), с перпендикулярными координатами ничего не происходит, и мы можем просто опустить их для краткости. Теперь, поскольку преобразование, которое мы рассматриваем, соединяет две инерциальные системы отсчета, оно должно преобразовать линейное движение в ( t , x ) в линейное движение в координатах ( t ′, x ′) . Следовательно, это должно быть линейное преобразование. Общий вид линейного преобразования:

$${\begin{bmatrix}t'\\x'\end{bmatrix}}={\begin{bmatrix}\gamma &\delta \\\beta &\alpha \end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}},$$

где α , β , γ и δ — некоторые пока неизвестные функции относительной скорости v .

Рассмотрим теперь движение начала системы отсчёта K ′. В системе K ′ он имеет координаты ( t ′, x ′ = 0) , а в системе K он имеет координаты ( t , x = vt ) . Эти две точки соединяются преобразованием

$${\begin{bmatrix}t'\\0\end{bmatrix}}={\begin{bmatrix}\gamma &\delta \\\beta &\alpha \end{bmatrix}}{\begin{bmatrix}t\\vt\end{bmatrix}},$$

из чего мы получаем

$$\beta =-v\alpha \,.$$

Аналогично, учитывая движение начала системы отсчёта К , получаем

$${\begin{bmatrix}t'\\-vt'\end{bmatrix}}={\begin{bmatrix}\gamma &\delta \\\beta &\alpha \end{bmatrix}}{\begin{bmatrix}t\\0\end{bmatrix}},$$

из чего мы получаем

$$\beta =-v\gamma \,.$$

Объединение этих двух значений дает α = γ , и матрица преобразования упрощается:

$${\begin{bmatrix}t'\\x'\end{bmatrix}}={\begin{bmatrix}\gamma &\delta \\-v\gamma &\gamma \end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}.$$

Теперь рассмотрим групповой постулат обратного элемента . Есть два способа перейти от системы координат K ′ к K. системе координат Первый — применить обратную матрицу преобразования к координатам K ′:

$${\begin{bmatrix}t\\x\end{bmatrix}}={\frac {1}{\gamma ^{2}+v\delta \gamma }}{\begin{bmatrix}\gamma &-\delta \\v\gamma &\gamma \end{bmatrix}}{\begin{bmatrix}t'\\x'\end{bmatrix}}.$$

Во-вторых, учитывая, что система координат K 'движется со скоростью v относительно системы координат K , система координат K должна двигаться со скоростью - v относительно системы координат K '. Замена v на − v в матрице преобразования дает:

$${\begin{bmatrix}t\\x\end{bmatrix}}={\begin{bmatrix}\gamma (-v)&\delta (-v)\\v\gamma (-v)&\gamma (-v)\end{bmatrix}}{\begin{bmatrix}t'\\x'\end{bmatrix}},$$

Теперь функция γ не может зависеть от направления v , поскольку, по-видимому, это фактор, определяющий релятивистское сжатие и замедление времени. Эти два (в нашем изотропном мире) не могут зависеть от направления v . Таким образом, γ (− v ) = γ ( v ) и, сравнивая две матрицы, получаем

$$\gamma ^{2}+v\delta \gamma =1.$$

Согласно постулату группы замыкания , композиция двух координатных преобразований также является координатным преобразованием, поэтому произведение двух наших матриц также должно быть матрицей того же вида. Преобразование K в K ' и из K ' в K ' дает следующую матрицу преобразования для перехода от K до K ':

$${\begin{aligned}{\begin{bmatrix}t''\\x''\end{bmatrix}}&={\begin{bmatrix}\gamma (v')&\delta (v')\\-v'\gamma (v')&\gamma (v')\end{bmatrix}}{\begin{bmatrix}\gamma (v)&\delta (v)\\-v\gamma (v)&\gamma (v)\end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}\\&={\begin{bmatrix}\gamma (v')\gamma (v)-v\delta (v')\gamma (v)&\gamma (v')\delta (v)+\delta (v')\gamma (v)\\-(v'+v)\gamma (v')\gamma (v)&-v'\gamma (v')\delta (v)+\gamma (v')\gamma (v)\end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}.\end{aligned}}$$

В исходной матрице преобразования оба основных диагональных элемента равны γ , следовательно, чтобы комбинированная матрица преобразования, указанная выше, имела ту же форму, что и исходная матрица преобразования, основные диагональные элементы также должны быть равны. Приравнивание этих элементов и перестановка дают:

$${\begin{aligned}\gamma (v')\gamma (v)-v\delta (v')\gamma (v)&=-v'\gamma (v')\delta (v)+\gamma (v')\gamma (v)\\v\delta (v')\gamma (v)&=v'\gamma (v')\delta (v)\\{\frac {\delta (v)}{v\gamma (v)}}&={\frac {\delta (v')}{v'\gamma (v')}}.\end{aligned}}$$

Знаменатель будет ненулевым для ненулевого v , потому что γ ( v ) всегда ненулевой;

$$\gamma ^{2}+v\delta \gamma =1.$$

Если v = 0, у нас есть единичная матрица, которая совпадает с помещением v = 0 в матрицу, которую мы получаем в конце этого вывода для других значений v , что делает окончательную матрицу действительной для всех неотрицательных v .

Для ненулевого v эта комбинация функций должна быть универсальной константой, одной и той же для всех инерциальных систем отсчета. Определим эту константу как δ ( v )/ v γ ( v ) = κ , где κ имеет размерность 1 / v ² . Решение

$$1=\gamma ^{2}+v\delta \gamma =\gamma ^{2}(1+\kappa v^{2})$$

мы наконец получаем

$$\gamma =1/{\sqrt {1+\kappa v^{2}}}$$

и, таким образом, матрица преобразования, согласующаяся с аксиомами группы, имеет вид

$${\begin{bmatrix}t'\\x'\end{bmatrix}}={\frac {1}{\sqrt {1+\kappa v^{2}}}}{\begin{bmatrix}1&\kappa v\\-v&1\end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}.$$

Если κ > 0 , то будут преобразования (при этом κv ² ≫ 1 ), преобразующие время в пространственную координату и наоборот. Мы исключаем это по физическим причинам, поскольку время может течь только в положительном направлении. Таким образом, два типа матриц трансформации согласуются с групповыми постулатами:

1. с универсальной постоянной κ = 0 и
2. с κ < 0 .

Преобразования Галилея

Если κ = 0 , то мы получаем кинематику Галилея-Ньютона с преобразованием Галилея:

$${\begin{bmatrix}t'\\x'\end{bmatrix}}={\begin{bmatrix}1&0\\-v&1\end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}\;,$$

где время абсолютно, t ′ = t , а относительная скорость v двух инерциальных систем отсчета не ограничена.

Преобразования Лоренца

Если κ < 0 , то полагаем $c=1/{\sqrt {-\kappa }}$ которая становится инвариантной скоростью , скоростью света в вакууме. Это дает κ = −1/ c ² и таким образом мы получаем специальную теорию относительности с преобразованием Лоренца

$${\begin{bmatrix}t'\\x'\end{bmatrix}}={\frac {1}{\sqrt {1-{v^{2} \over c^{2}}}}}{\begin{bmatrix}1&{-v \over c^{2}}\\-v&1\end{bmatrix}}{\begin{bmatrix}t\\x\end{bmatrix}}\;,$$

где скорость света — это конечная универсальная константа, определяющая максимально возможную относительную скорость между инерциальными системами отсчета.

Если v ≪ c, преобразование Галилея является хорошим приближением преобразования Лоренца.

Только эксперимент может ответить на вопрос, какая из двух возможностей — κ = 0 или κ < 0 — реализуется в нашем мире. Эксперименты по измерению скорости света, впервые проведенные датским физиком Оле Рёмером , показывают, что она конечна, а эксперимент Майкельсона-Морли показал, что это абсолютная скорость и, следовательно, что κ <0 .

Повышение от генераторов

Используя быстроту φ для параметризации преобразования Лоренца, усиление в направлении x равно

$${\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &-\sinh \phi &0&0\\-\sinh \phi &\cosh \phi &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}},$$

аналогично для повышения в y направлении

$${\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &0&-\sinh \phi &0\\0&1&0&0\\-\sinh \phi &0&\cosh \phi &0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}},$$

и z направление

$${\begin{bmatrix}ct'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &0&0&-\sinh \phi \\0&1&0&0\\0&0&1&0\\-\sinh \phi &0&0&\cosh \phi \\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}\,.$$

где e _x , e _y , e _z — декартовы базисные векторы, набор взаимно перпендикулярных единичных векторов вдоль указанных направлений. Если один кадр ускоряется со скоростью v относительно другого, удобно ввести единичный вектор n = v / v = β / β в направлении относительного движения. Общий импульс

$${\begin{bmatrix}c\,t'\\x'\\y'\\z'\end{bmatrix}}={\begin{bmatrix}\cosh \phi &-n_{x}\sinh \phi &-n_{y}\sinh \phi &-n_{z}\sinh \phi \\-n_{x}\sinh \phi &1+(\cosh \phi -1)n_{x}^{2}&(\cosh \phi -1)n_{x}n_{y}&(\cosh \phi -1)n_{x}n_{z}\\-n_{y}\sinh \phi &(\cosh \phi -1)n_{y}n_{x}&1+(\cosh \phi -1)n_{y}^{2}&(\cosh \phi -1)n_{y}n_{z}\\-n_{z}\sinh \phi &(\cosh \phi -1)n_{z}n_{x}&(\cosh \phi -1)n_{z}n_{y}&1+(\cosh \phi -1)n_{z}^{2}\\\end{bmatrix}}{\begin{bmatrix}c\,t\\x\\y\\z\end{bmatrix}}\,.$$

Обратите внимание, что матрица зависит от направления относительного движения, а также от скорости во всех трех числах (два для направления, одно для скорости).

Мы можем привести каждую из матриц повышения в другую форму следующим образом. Сначала рассмотрим повышение в направлении x . Разложение Тейлора матрицы повышения относительно φ = 0 равно

$$B(\mathbf {e} _{x},\phi )=\sum _{n=0}^{\infty }{\frac {\phi ^{n}}{n!}}\left.{\frac {\partial ^{n}B(\mathbf {e} _{x},\phi )}{\partial \phi ^{n}}}\right|_{\phi =0}$$

где производные матрицы по φ определяются путем дифференцирования каждого элемента матрицы отдельно, а обозначение | _{φ = 0} указывает, что φ устанавливается в ноль после вычисления производных. Расширение до первого порядка дает бесконечно малое преобразование

$$B(\mathbf {e} _{x},\phi )=I+\phi \left.{\frac {\partial B}{\partial \phi }}\right|_{\phi =0}={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}-\phi {\begin{bmatrix}0&1&0&0\\1&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}$$

что справедливо, если φ мало (следовательно, φ ² и более высокие степени пренебрежимо малы) и могут быть интерпретированы как отсутствие повышения (первый член I представляет собой единичную матрицу 4×4), за которым следует небольшое повышение. Матрица

$$K_{x}={\begin{bmatrix}0&1&0&0\\1&0&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}$$

является генератором повышения в направлении x , поэтому бесконечно малое повышение равно

$$B(\mathbf {e} _{x},\phi )=I-\phi K_{x}$$

Теперь φ мало, поэтому деление на положительное целое число N дает еще меньшее приращение быстроты φ / N , а N этих бесконечно малых ускорений даст исходное бесконечно малое ускорение с быстротой φ ,

$$B(\mathbf {e} _{x},\phi )=\left(I-{\frac {\phi K_{x}}{N}}\right)^{N}$$

В пределе бесконечного числа бесконечно малых шагов мы получаем конечное буст-преобразование

$$B(\mathbf {e} _{x},\phi )=\lim _{N\to \infty }\left(I-{\frac {\phi K_{x}}{N}}\right)^{N}=e^{-\phi K_{x}}$$

что является предельным определением экспоненты, данным Леонардом Эйлером , и теперь верно для любого φ .

Повторение процесса для повышения в направлениях y и z дает другие генераторы.

$$K_{y}={\begin{bmatrix}0&0&1&0\\0&0&0&0\\1&0&0&0\\0&0&0&0\end{bmatrix}}\,,\quad K_{z}={\begin{bmatrix}0&0&0&1\\0&0&0&0\\0&0&0&0\\1&0&0&0\end{bmatrix}}$$

и повышения есть

$$B(\mathbf {e} _{y},\phi )=e^{-\phi K_{y}}\,,\quad B(\mathbf {e} _{z},\phi )=e^{-\phi K_{z}}\,.$$

Для любого направления бесконечно малое преобразование (малое φ и разложение до первого порядка)

$$B(\mathbf {n} ,\phi )=I+\phi \left.{\frac {\partial B}{\partial \phi }}\right|_{\phi =0}={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}-\phi {\begin{bmatrix}0&n_{x}&n_{y}&n_{z}\\n_{x}&0&0&0\\n_{y}&0&0&0\\n_{z}&0&0&0\end{bmatrix}}$$

где

$${\begin{bmatrix}0&n_{x}&n_{y}&n_{z}\\n_{x}&0&0&0\\n_{y}&0&0&0\\n_{z}&0&0&0\end{bmatrix}}=n_{x}K_{x}+n_{y}K_{y}+n_{z}K_{z}=\mathbf {n} \cdot \mathbf {K}$$

является генератором повышения в направлении n . Это генератор полного повышения, вектор матриц K = ( K _x , K _y , K _z ) , спроецированный в направлении повышения n . Бесконечно малый импульс

$$B(\mathbf {n} ,\phi )=I-\phi (\mathbf {n} \cdot \mathbf {K} )$$

Тогда в пределе бесконечного числа бесконечно малых шагов мы получаем конечное буст-преобразование

$$B(\mathbf {n} ,\phi )=\lim _{N\to \infty }\left(I-{\frac {\phi (\mathbf {n} \cdot \mathbf {K} )}{N}}\right)^{N}=e^{-\phi (\mathbf {n} \cdot \mathbf {K} )}$$

что теперь верно для любого φ . Разложение матричной экспоненты − ( φ ⋅ n в K ) степенной ряд

$$e^{-\phi \mathbf {n} \cdot \mathbf {K} }=\sum _{n=0}^{\infty }{\frac {1}{n!}}(-\phi \mathbf {n} \cdot \mathbf {K} )^{n}$$

теперь нам нужны мощности генератора. Площадь

$$(\mathbf {n} \cdot \mathbf {K} )^{2}={\begin{bmatrix}1&0&0&0\\0&n_{x}^{2}&n_{x}n_{y}&n_{x}n_{z}\\0&n_{y}n_{x}&n_{y}^{2}&n_{y}n_{z}\\0&n_{z}n_{x}&n_{z}n_{y}&n_{z}^{2}\end{bmatrix}}$$

но куб ( п ⋅ К ) ³ возвращается к ( n ⋅ K ) , и как всегда нулевая степень - это тождество 4×4, ( n ⋅ K ) ⁰ = Я. ​В общем случае нечетные степени n = 1, 3, 5,... равны

$$(\mathbf {n} \cdot \mathbf {K} )^{n}=(\mathbf {n} \cdot \mathbf {K} )$$

а четные степени n = 2, 4, 6, ...

$$(\mathbf {n} \cdot \mathbf {K} )^{n}=(\mathbf {n} \cdot \mathbf {K} )^{2}$$

поэтому явный вид матрицы повышения зависит только от генератора и его квадрата. Разделение степенного ряда на нечетный и четный степенной ряд с использованием нечетных и четных степеней генератора, а также ряда Тейлора sinh φ и cosh φ около φ = 0 позволяет получить более компактную, но подробную форму матрицы повышения.

$${\begin{aligned}e^{-\phi \mathbf {n} \cdot \mathbf {K} }&=-\sum _{n=1,3,5\ldots }^{\infty }{\frac {1}{n!}}\phi ^{n}(\mathbf {n} \cdot \mathbf {K} )^{n}+\sum _{n=0,2,4\ldots }^{\infty }{\frac {1}{n!}}\phi ^{n}(\mathbf {n} \cdot \mathbf {K} )^{n}\\&=-\left[\phi +{\frac {\phi ^{3}}{3!}}+{\frac {\phi ^{5}}{5!}}+\cdots \right](\mathbf {n} \cdot \mathbf {K} )+I+\left[-1+1+{\frac {1}{2!}}\phi ^{2}+{\frac {1}{4!}}\phi ^{4}+{\frac {1}{6!}}\phi ^{6}+\cdots \right](\mathbf {n} \cdot \mathbf {K} )^{2}\\&=-\sinh \phi (\mathbf {n} \cdot \mathbf {K} )+I+(-1+\cosh \phi )(\mathbf {n} \cdot \mathbf {K} )^{2}\end{aligned}}$$

где 0 = −1 + 1 вводится для четного степенного ряда, чтобы дополнить ряд Тейлора для ch φ . Повышение похоже на формулу вращения Родригеса :

$$B(\mathbf {n} ,\phi )=e^{-\phi \mathbf {n} \cdot \mathbf {K} }=I-\sinh \phi (\mathbf {n} \cdot \mathbf {K} )+(\cosh \phi -1)(\mathbf {n} \cdot \mathbf {K} )^{2}\,.$$

Отрицание быстроты в экспоненте дает матрицу обратного преобразования:

$$B(\mathbf {n} ,-\phi )=e^{\phi \mathbf {n} \cdot \mathbf {K} }=I+\sinh \phi (\mathbf {n} \cdot \mathbf {K} )+(\cosh \phi -1)(\mathbf {n} \cdot \mathbf {K} )^{2}\,.$$

В квантовой механике , релятивистской квантовой механике и квантовой теории поля для генераторов повышения используется другое соглашение; все повышающие генераторы умножаются на коэффициент мнимой единицы i = √ −1 .

Из экспериментов

Основная статья: Проверка теории специальной теории относительности

Говард Перси Робертсон и другие показали, что преобразование Лоренца также можно вывести эмпирически. Для этого необходимо записать преобразования координат, включающие экспериментально проверяемые параметры. Например, пусть дана одна «предпочтительная» инерциальная система отсчета. $X,Y,Z,T$ скорость света постоянна, изотропна и не зависит от скорости источника. Также предполагается, что синхронизация Эйнштейна и синхронизация посредством медленной тактовой передачи эквивалентны в этом кадре. Затем предположим другой кадр $x,y,z,t$ в относительном движении, при котором часы и стержни имеют то же внутреннее строение, что и в предпочтительной системе отсчета. Однако следующие отношения остаются неопределенными:

• $a(v)$ различия в измерениях времени,
• $b(v)$ различия в измеренных продольных длинах,
• $d(v)$ различия в измеренных поперечных длинах,
• $\varepsilon (v)$ зависит от процедуры синхронизации часов в движущейся системе отсчета,

тогда формулы преобразования (предполагаемые линейными) между этими кадрами задаются следующим образом:

$${\begin{aligned}t&=a(v)T+\varepsilon (v)x\\x&=b(v)(X-vT)\\y&=d(v)Y\\z&=d(v)Z\end{aligned}}$$

$\varepsilon (v)$ зависит от соглашения о синхронизации и не определяется экспериментально, оно получает значение $-v/c^{2}$ используя синхронизацию Эйнштейна в обоих кадрах. Соотношение между $b(v)$ и $d(v)$ определяется экспериментом Майкельсона–Морли , соотношение между $a(v)$ и $b(v)$ определяется экспериментом Кеннеди-Торндайка и $a(v)$ определяется только экспериментом Айвза-Стилвелла . Таким образом, они были определены с большой точностью, чтобы $1/a(v)=b(v)=\gamma$ и $d(v)=1$, который преобразует указанное выше преобразование в преобразование Лоренца.

См. также

• группа Лоренца
• Теорема Нётер
• Группа Пуанкаре
• подходящее время
• Релятивистская метрика
• Спинор

Ссылки

• Грейнер, В .; Бромли, Д.А. (2000). Релятивистская квантовая механика (3-е изд.). спрингер. ISBN  9783540674573 .
• Ландау, LD ; Лифшиц, Э.М. (2002) [1939]. Классическая теория полей . Курс теоретической физики. Том. 2 (4-е изд.). Баттерворт-Хайнеманн . ISBN  0-7506-2768-9 .
• Вайнберг, С. (2002), Квантовая теория полей , том. 1, Издательство Кембриджского университета , ISBN  0-521-55001-7