Эксперимент Кеннеди-Торндайка

Рисунок 1. Эксперимент Кеннеди–Торндайка.

Эксперимент Кеннеди-Торндайка , впервые проведенный в 1932 году Роем Дж. Кеннеди и Эдвардом М. Торндайком, представляет собой модифицированную форму экспериментальной процедуры Майкельсона-Морли , проверяющую специальную теорию относительности . Модификация заключается в том, чтобы одно плечо классического аппарата Майкельсона-Морли (ММ) сделать короче другого. В то время как эксперимент Майкельсона-Морли показал, что скорость света не зависит от ориентации аппарата, эксперимент Кеннеди-Торндайка показал, что она также не зависит от скорости аппарата в различных инерциальных системах отсчета. Он также служил тестом для косвенной проверки замедления времени : хотя отрицательный результат эксперимента Майкельсона-Морли можно объяснить только сокращением длины , отрицательный результат эксперимента Кеннеди-Торндайка требует замедления времени в дополнение к сокращению длины, чтобы объяснить, почему никакие фазовые сдвиги не будут обнаружены во время движения Земли вокруг Солнца. Первое прямое подтверждение замедления времени было получено экспериментом Айвза-Стилвелла . Объединив результаты этих трех экспериментов, полное преобразование Лоренца . можно получить

Усовершенствованные варианты эксперимента Кеннеди-Торндайка были проведены с использованием оптических резонаторов или лунной лазерной локации . Общий обзор тестов Лоренц-инвариантности см. в разделе Тесты специальной теории относительности .

Эксперимент

Первоначальный эксперимент Майкельсона-Морли был полезен только для проверки гипотезы сокращения Лоренца-Фитцджеральда . нашел способ проверить замедление времени Кеннеди уже сделал несколько более сложных версий эксперимента ММ в 1920-х годах, когда он также . По их собственным словам:

Принцип, на котором основан этот эксперимент, заключается в простом предположении, что если луч однородного света разделяется […] на два луча, которые после прохождения путей разной длины снова сближаются, то относительные фазы […] будут зависеть [… ] от скорости аппарата, если только частота света не зависит […] от скорости, как того требует теория относительности.

Как показано на рис. 1, ключевые оптические компоненты были установлены внутри вакуумной камеры V на основе из плавленого кварца с чрезвычайно низким коэффициентом теплового расширения . Водяная рубашка W поддерживала температуру с точностью до 0,001 °C. Монохроматический зеленый свет от ртутного источника Hg проходил через поляризационную призму Николя N перед входом в вакуумную камеру и разделялся светоделителем B , установленным под углом Брюстера, чтобы предотвратить нежелательные отражения от задней поверхности. Два луча были направлены на два зеркала М ₁ и М ₂ , которые были установлены на максимально расходящихся расстояниях, учитывая длину когерентности линии ртути 5461 Å (≈32 см, что допускает разницу в длине плеч Δ L ≈ 16 см). Отраженные лучи рекомбинировались, образуя круговые интерференционные полосы , которые были сфотографированы при P . Щель S позволяла записывать несколько экспозиций по диаметру колец на одной фотографической пластинке в разное время суток.

Сделав одно плечо эксперимента намного короче другого, изменение скорости Земли вызовет изменения во времени прохождения световых лучей, в результате чего произойдет сдвиг полосы, если только частота источника света не изменится на ту же самую. степень. Чтобы определить, имело ли место такое смещение полос , интерферометр сделали предельно стабильным и интерференционные картины сфотографировали для последующего сравнения. Испытания проводились в течение многих месяцев. Поскольку не было обнаружено значительного смещения полос (что соответствует скорости 10±10 км/с в пределах погрешности), экспериментаторы пришли к выводу, что замедление времени происходит, как предсказывает Специальная теория относительности.

Теория

Основная теория эксперимента

Рисунок 2. Путь света Кеннеди – Торндайка с использованием перпендикулярных плеч.

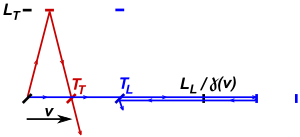
Хотя сокращение Лоренца-Фитцджеральда (сокращение Лоренца) само по себе полностью способно объяснить нулевые результаты эксперимента Майкельсона-Морли, само по себе оно не может объяснить нулевые результаты эксперимента Кеннеди-Торндайка. Сокращение Лоренца – Фитцджеральда определяется формулой:

$L=L_{0}{\sqrt {1-v^{2}/c^{2}}}=L_{0}/{\gamma (v)}$

где

$L_{0}$ — правильная длина (длина объекта в кадре покоя),

$L$ - длина, наблюдаемая наблюдателем при относительном движении относительно объекта,

$v\,$ - относительная скорость между наблюдателем и движущимся объектом, т.е. между гипотетическим эфиром и движущимся объектом.

$c\,$ это скорость света ,

а фактор Лоренца определяется как

$\gamma (v)\equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}}\$.

Рис. 2 иллюстрирует аппарат Кеннеди-Торндайка с перпендикулярными плечами и предполагает справедливость сокращения Лоренца. Если аппарат неподвижен относительно гипотетического эфира, разница во времени, за которое свет проходит через продольное и поперечное плечи, определяется выражением:

$T_{L}-T_{T}={\frac {2(L_{L}-L_{T})}{c}}$

Время, необходимое свету для перемещения вперед и назад по длине продольного плеча, сокращенному по Лоренцу, определяется выражением:

$T_{L}=T_{1}+T_{2}={\frac {L_{L}/\gamma (v)}{c-v}}+{\frac {L_{L}/\gamma (v)}{c+v}}={\frac {2L_{L}/\gamma (v)}{c}}{\frac {1}{1-{\frac {v^{2}}{c^{2}}}}}={\frac {2L_{L}\gamma (v)}{c}}$

где Т ₁ – время прохождения в направлении движения, Т ₂ – в противоположном направлении, v – составляющая скорости относительно светоносного эфира, с – скорость света, L _{L –} длина продольного плеча интерферометра. Время, необходимое свету для прохождения поперечного плеча и обратно, определяется по формуле:

$T_{T}={\frac {2L_{T}}{\sqrt {c^{2}-v^{2}}}}={\frac {2L_{T}}{c}}{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {2L_{T}\gamma (v)}{c}}$

Разница во времени, за которое свет проходит через продольное и поперечное плечи, определяется выражением:

$T_{L}-T_{T}={\frac {2(L_{L}-L_{T})\gamma (v)}{c}}$

Поскольку Δ L=c(T _L -T _T ) , заданы следующие различия в длине хода (Δ L _A представляет собой начальную разницу в длине хода, а v _{A -} начальную скорость устройства, а Δ L _B и v _B после вращения или изменение скорости из-за собственного вращения Земли или ее вращения вокруг Солнца):

$\Delta L_{A}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{A}^{2}/c^{2}}}},\qquad \Delta L_{B}={\frac {2\left(L_{L}-L_{T}\right)}{\sqrt {1-v_{B}^{2}/c^{2}}}}$.

Чтобы получить отрицательный результат, мы должны иметь Δ L _A −Δ L _B =0. Однако можно видеть, что обе формулы отменяют друг друга только до тех пор, пока скорости одинаковы ( v _A = v _B ). Но если скорости разные, то Δ L _A и Δ L _B уже не равны. (На эксперимент Майкельсона-Морли изменения скорости не влияют, поскольку разница между L _L и L _T равна нулю. Следовательно, эксперимент ММ только проверяет, зависит ли скорость света от ориентации аппарата.) Но в эксперименте Кеннеди – В эксперименте Торндайка длины L _L и L _T изначально различны, поэтому он также способен измерить зависимость скорости света от скорости аппарата.

Согласно предыдущей формуле, разность длин пробега Δ L _A −Δ L _B и, следовательно, ожидаемый сдвиг полосы Δ N определяются по формуле (λ — длина волны):

$\Delta N={\frac {\Delta L_{A}-\Delta L_{B}}{\lambda }}={\frac {2\left(L_{L}-L_{T}\right)}{\lambda }}\left({\frac {1}{\sqrt {1-v_{A}^{2}/c^{2}}}}-{\frac {1}{\sqrt {1-v_{B}^{2}/c^{2}}}}\right)$.

Пренебрегая величинами выше второго порядка по v/c :

$\approx {\frac {L_{L}-L_{T}}{\lambda }}\left({\frac {v_{A}^{2}-v_{B}^{2}}{c^{2}}}\right)$

Для постоянного Δ N , т.е. для того, чтобы сдвиг полосы не зависел от скорости или ориентации устройства, необходимо, чтобы частота и, следовательно, длина волны λ были изменены с помощью фактора Лоренца. влияние замедления времени На самом деле это тот случай, когда рассматривается на частоту. Следовательно, для объяснения отрицательного результата эксперимента Кеннеди-Торндайка необходимы как сокращение длины, так и замедление времени.

Важность теории относительности

показали В 1905 году Анри Пуанкаре и Альберт Эйнштейн , что преобразование Лоренца должно образовывать группу , чтобы удовлетворять принципу относительности (см. Историю преобразований Лоренца ). Для этого необходимо, чтобы сокращение длины и замедление времени имели точные релятивистские значения. Кеннеди и Торндайк теперь утверждали, что они могут получить полное преобразование Лоренца исключительно на основе экспериментальных данных эксперимента Майкельсона-Морли и эксперимента Кеннеди-Торндайка. Но это не совсем верно, поскольку сокращение длины и замедление времени, имеющие точные релятивистские значения, достаточны, но не обязательны для объяснения обоих экспериментов. Это связано с тем, что сокращение длины исключительно в направлении движения — это только одна возможность объяснить эксперимент Майкельсона-Морли. В общем, его нулевой результат требует, чтобы соотношение поперечной и продольной длин соответствовало фактору Лоренца, который включает в себя бесконечное количество комбинаций изменений длины в поперечном и продольном направлении. Это также влияет на роль замедления времени в эксперименте Кеннеди-Торндайка, поскольку его значение зависит от величины сокращения длины, используемой при анализе эксперимента. Поэтому необходимо рассмотреть третий эксперимент, Эксперимент Айвса-Стилуэлла , чтобы вывести преобразование Лоренца только на основе экспериментальных данных.

Точнее: В рамках теории критериев Робертсона-Мансури-Сексла , Для описания экспериментов можно использовать следующую схему: α представляет собой изменения во времени, β — изменения длины в направлении движения, а δ — изменения длины перпендикулярно направлению движения. Эксперимент Майкельсона-Морли проверяет связь между β и δ, а эксперимент Кеннеди-Торндайка проверяет связь между α и β. Таким образом, α зависит от β, которое в свою очередь зависит от δ, и в этих двух экспериментах можно измерить только комбинации этих величин, но не их отдельные значения. необходим еще один эксперимент Для непосредственного измерения значения одной из этих величин . Фактически это было достигнуто с помощью эксперимента Айвса-Стилвелла, в ходе которого было измерено значение α, предсказанное релятивистским замедлением времени. Объединение этого значения для α с нулевым результатом Кеннеди – Торндайка показывает, что β обязательно должно принимать значение релятивистского сокращения длины. А объединение этого значения для β с нулевым результатом Майкельсона–Морли показывает, что δ должно быть равно нулю. Таким образом, необходимые компоненты преобразования Лоренца обеспечиваются экспериментально, в соответствии с теоретическими требованиями теория групп .

Недавние эксперименты

Дополнительная информация: Современные поиски нарушения Лоренца.

Тесты полости

Рисунок 3. Упрощенная диаграмма Braxmaier et al. 2002 г.

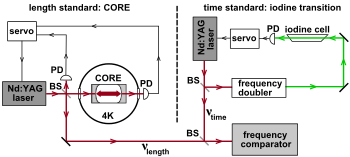
В последние годы эксперименты Майкельсона-Морли , а также эксперименты типа Кеннеди-Торндайка были повторены с повышенной точностью с использованием лазеров , мазеров и криогенных оптических резонаторов . Границы зависимости скорости согласно теории испытаний Робертсона-Мансури-Сексла (RMS), которая указывает на связь между замедлением времени и сокращением длины, были значительно улучшены. Например, первоначальный эксперимент Кеннеди-Торндайка установил границы зависимости среднеквадратической скорости от скорости ~ 10 ⁻² , но текущие ограничения находятся в пределах ~10 ⁻⁸ диапазон.

На рис. 3 представлена ​​упрощенная схематическая диаграмма Браксмайером и др. в 2002 году. повторения эксперимента Кеннеди-Торндайка, проведенного Слева фотодетекторы (ФД) контролируют резонанс эталона длины сапфирового криогенного оптического резонатора (CORE), хранящегося при температуре жидкого гелия для стабилизации частоты Nd:YAG-лазера до 1064 нм. Справа линия поглощения 532 нм эталонного йода низкого давления используется в качестве стандарта времени для стабилизации (удвоенной) частоты второго Nd:YAG-лазера.

Автор	Год	Описание	Максимум зависимость от скорости
Хилс и Холл	1990	Сравнение частоты оптического резонатора Фабри–Перо с частотой лазера, стабилизированного по опорной линии I 2 .	$\lesssim 10^{-5}$
Браксмайер и др.	2002	Сравнение частоты криогенного оптического резонатора со стандартом частоты I 2 с использованием двух лазеров Nd:YAG .
Вольф и др.	2003	Частота стационарного криогенного микроволнового генератора, состоящего из сапфирового кристалла, работающего в режиме шепчущей галереи , сравнивается с частотой водородного мазера , частоту которого сравнивают с часами на цезии и рубидии атомными фонтанными . Были найдены изменения во время вращения Земли. Были проанализированы данные за 2001–2002 годы.	$\lesssim 10^{-7}$
Вольф и др.	2004	См. Вольф и др. (2003). Реализован активный контроль температуры. Были проанализированы данные за 2002–2003 годы.
Тобар и др.	2009	См. Вольф и др. (2003). Данные за 2002–2008 годы были проанализированы как на предмет сидерических, так и годовых вариаций.	$\lesssim 10^{-8}$

Лунная лазерная локация

Помимо наземных измерений, эксперименты Кеннеди-Торндайка были проведены Мюллером и Соффелем (1995). и Мюллер и др. (1999) с использованием данных лунной лазерной локации , в которых расстояние Земля-Луна оценивается с точностью до сантиметров. Если существует предпочтительная система отсчета и скорость света зависит от скорости наблюдателя, то при измерениях расстояний Земля-Луна должны наблюдаться аномальные колебания. Поскольку замедление времени уже подтверждено с высокой точностью, наблюдение таких колебаний продемонстрирует зависимость скорости света от скорости наблюдателя, а также зависимость сокращения длины от направления. Однако ни в одном из исследований таких колебаний не наблюдалось, при этом среднеквадратичная граница скорости составляла ~10 ⁻⁵ , сопоставимо с границами, установленными Хилсом и Холлом (1990). Следовательно, и сокращение длины, и замедление времени должны иметь значения, предсказанные теорией относительности.