Замедление времени

Эта статья о физической концепции. Чтобы узнать о термине, используемом в психологии, см. « Восприятие времени» .

Замедление времени — это разница в прошедшем времени , измеренная двумя часами, либо из-за относительной скорости между ними ( специальная теория относительности ), либо из-за разницы в гравитационном потенциале между их местоположениями ( общая теория относительности ). Если не указано иное, «замедление времени» обычно относится к эффекту, обусловленному скоростью.

После компенсации различных задержек сигнала, возникающих в результате изменения расстояния между наблюдателем и движущимися часами (т. е. эффект Доплера наблюдателя ), наблюдатель будет измерять движущиеся часы как тикающие медленнее, чем часы, находящиеся в состоянии покоя в собственной системе отсчета . Кроме того, часы, находящиеся близко к массивному телу (и, следовательно, имеющие более низкий гравитационный потенциал), будут регистрировать меньшее прошедшее время, чем часы, расположенные дальше от того же массивного тела (и имеющие более высокий гравитационный потенциал).

Эти предсказания теории относительности неоднократно подтверждались экспериментом и имеют практическое значение, например, при работе спутниковых навигационных систем, таких как GPS и Galileo .

История

Основная статья: История специальной теории относительности

Замедление времени фактором Лоренца было предсказано несколькими авторами на рубеже 20-го века. Джозеф Лармор (1897) писал, что, по крайней мере для тех, кто вращается вокруг ядра, отдельные электроны описывают соответствующие части своих орбит за времена, более короткие для [остальной] системы в соотношении: ${\textstyle {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$. Эмиль Кон (1904) специально связал эту формулу со скоростью часов. В контексте специальной теории относительности (1905) показал Альберт Эйнштейн , что этот эффект касается природы самого времени, и он также был первым, кто указал на его взаимность или симметрию. Впоследствии Герман Минковский (1907) ввел концепцию собственного времени , которая еще больше прояснила значение замедления времени.

вызванное относительной

Смотрите также: Специальная теория относительности § Замедление времени

В локальной системе отсчета синих часов красные часы, находящиеся в движении, воспринимаются как тикающие медленнее.

Специальная теория относительности показывает, что для наблюдателя в инерциальной системе отсчета часы, движущиеся относительно наблюдателя, будут идти медленнее, чем часы, находящиеся в состоянии покоя в системе отсчета наблюдателя. Иногда это называют специальным релятивистским замедлением времени. Чем выше относительная скорость , тем больше замедление времени между ними, причем время замедляется до остановки, когда одни часы приближаются к скорости света (299 792 458 м/с).

Теоретически замедление времени позволило бы пассажирам быстро движущегося транспортного средства переместиться в будущее за короткий период своего времени. При достаточно высоких скоростях эффект был бы впечатляющим. Например, один год путешествия может соответствовать десяти годам пребывания на Земле. Действительно, постоянное ускорение в 1 g позволило бы людям путешествовать через всю известную Вселенную за одну человеческую жизнь.

Учитывая, что современные технологии жестко ограничивают скорость космических путешествий, различия, наблюдаемые на практике, незначительны. За 6 месяцев пребывания на Международной космической станции (МКС), вращающейся вокруг Земли со скоростью около 7700 м/с, астронавт постарел бы примерно на 0,005 секунды меньше, чем на Земле. Космонавты Сергей Крикалев и Сергей Авдеев испытали замедление времени примерно на 20 миллисекунд по сравнению со временем, прошедшим на Земле.

Простой вывод

Слева : наблюдатель в состоянии покоя измеряет время 2 L / c между локальными событиями генерации светового сигнала в точке A и прибытия в точку A.
Справа : события по мнению наблюдателя, движущегося слева от установки: нижнее зеркало A, когда сигнал генерируется в момент времени t'= 0, верхнее зеркало B, когда сигнал отражается в момент времени t'=D/c , нижнее зеркало A, когда сигнал возвращается в момент времени t'=2D/c

Замедление времени можно вывести из наблюдаемого постоянства скорости света во всех системах отсчета, продиктованного вторым постулатом специальной теории относительности . Это постоянство скорости света означает, что, вопреки интуиции, скорости материальных объектов и света не суммируются. Невозможно увеличить скорость света, перемещаясь к источнику света или от него.

Рассмотрим теперь простые вертикальные часы, состоящие из двух зеркал A и B , между которыми отражается световой импульс. Расстояние между зеркалами равно L и часы тикают один раз каждый раз, когда световой импульс попадает на зеркало A. ,

В кадре, в котором часы покоятся (см. левую часть схемы), световой импульс прочерчивает путь длиной 2 L и периодом времени между тактами часов $\Delta t$ равен 2 L, делённому на скорость света c :

$\Delta t={\frac {2L}{c}}$

В системе отсчета движущегося наблюдателя, движущегося со скоростью v относительно покоящейся системы часов (правая часть диаграммы), световой импульс рассматривается как прослеживающий более длинный наклонный путь 2 D . Поддержание постоянной скорости света для всех инерциальных наблюдателей требует удлинения (то есть расширения) периода времени между тиканьем этих часов. $\Delta t'$ с точки зрения движущегося наблюдателя. То есть, если измерять кадр, движущийся относительно локальных часов, эти часы будут работать (то есть тикать) медленнее, поскольку частота тактов равна единице за период времени между тактами 1/ $\Delta t'$.

Прямое применение теоремы Пифагора приводит к известному предсказанию специальной теории относительности:

Общее время, в течение которого световой импульс прослеживает свой путь, определяется выражением:

$\Delta t'={\frac {2D}{c}}$

Длину полупути можно рассчитать как функцию известных величин:

$D={\sqrt {\left({\frac {1}{2}}v\Delta t'\right)^{2}+L^{2}}}$

Исключение переменных D и L из этих трех уравнений приводит к:

Уравнение замедления времени

$\Delta t'={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\gamma }{\Delta t}$

что выражает тот факт, что период часов движущегося наблюдателя $\Delta t'$ больше, чем период $\Delta t$ в рамке самих часов. Фактор Лоренца гамма ( γ ) определяется как

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

Поскольку все часы, имеющие общий период в системе покоя, должны иметь общий период при наблюдении из движущейся системы отсчета, все остальные часы — механические, электронные, оптические (например, идентичная горизонтальная версия часов в примере) — должны демонстрировать такое же замедление времени, зависящее от скорости.

Взаимность

Трансверсальное замедление времени. Синие точки представляют собой импульс света. Каждая пара точек, между которыми «прыгает» свет, — это часы. В рамках каждой группы часов другая группа тикает медленнее, потому что световой импульс движущихся часов должен пройти большее расстояние, чем световой импульс неподвижных часов. Это так, хотя часы идентичны и их относительное движение совершенно взаимно.

Учитывая определенную систему отсчета и «неподвижного» наблюдателя, описанного ранее, если бы второй наблюдатель сопровождал «движущиеся» часы, каждый из наблюдателей воспринимал бы часы другого как тикающие с более медленной скоростью, чем их собственные локальные часы, из-за они оба воспринимают другого как того, кто находится в движении относительно их собственной стационарной системы отсчета.

Здравый смысл подсказывает, что, если течение времени для движущегося объекта замедлилось, этот объект будет наблюдать, что время внешнего мира соответственно ускорится. Как ни странно, специальная теория относительности предсказывает обратное. Когда два наблюдателя движутся относительно друг друга, каждый будет измерять замедление часов другого в соответствии с тем, что они движутся относительно системы отсчета наблюдателя.

Время UV часов в S короче по сравнению с Ux' в S', а время UW часов в S' короче по сравнению с Ux в S.

Хотя это кажется противоречивым, подобная странность встречается и в повседневной жизни. Если два человека A и B наблюдают друг за другом на расстоянии, B покажется A маленьким, но в то же время A покажется маленьким B. Зная влияние перспективы , в этой ситуации нет противоречия или парадокса. .

Взаимность этого явления также приводит к так называемому парадоксу близнецов , когда сравнивается старение близнецов, один из которых остается на Земле, а другой отправляется в космическое путешествие, и где взаимность предполагает, что оба человека должны быть одного возраста, когда они воссоединиться. Напротив, в конце путешествия туда и обратно путешествующий близнец будет моложе своего брата на Земле. Дилемму, которую ставит парадокс, можно объяснить тем, что ситуация не симметрична. Находящийся на Земле двойник находится в одной инерциальной системе отсчета, а путешествующий двойник — в двух разных инерциальных системах: одна на выходе, другая — на обратном пути. См. также Парадокс близнецов#Роль ускорения .

Экспериментальное тестирование

Основная статья: Экспериментальное тестирование замедления времени

Смотрите также: Тесты специальной теории относительности

Движущиеся частицы

• сравнение времен жизни мюонов Возможно на разных скоростях. В лаборатории производятся медленные мюоны; а в атмосферу космические лучи приносят очень быстро движущиеся мюоны. Если принять время жизни мюона в состоянии покоя за лабораторное значение 2,197 мкс, то время жизни мюона, рожденного космическими лучами и движущегося со скоростью 98% скорости света, примерно в пять раз больше, что согласуется с наблюдениями. Примером может служить Росси и Холл (1941), которые сравнили популяцию мюонов, рожденных космическими лучами на вершине горы, с популяцией, наблюдаемой на уровне моря.
• Время жизни частиц, производимых в ускорителях частиц, увеличивается из-за замедления времени. В таких экспериментах «часы» — это время, затрачиваемое на процессы, ведущие к распаду мюона, и эти процессы происходят в движущемся мюоне с его собственной «тактовой частотой», которая значительно медленнее, чем у лабораторных часов. Это обычно учитывается в физике элементарных частиц, и было проведено множество специальных измерений. Например, в кольце хранения мюонов в ЦЕРН было обнаружено, что время жизни мюонов, циркулирующих с γ = 29,327, расширено до 64,378 мкс, что подтверждает замедление времени с точностью 0,9 ± 0,4 частей на тысячу.

Эффект Доплера

Основная статья: эксперимент Айвза – Стилвелла

• Заявленная цель этих экспериментов Айвза и Стилвелла (1938, 1941) состояла в том, чтобы проверить эффект замедления времени, предсказанный теорией эфира Лармора-Лоренца, вследствие движения в эфире, используя предположение Эйнштейна о том, что эффект Доплера в канальных лучах обеспечит подходящее эксперимент. В этих экспериментах измерялся доплеровский сдвиг излучения, испускаемого катодными лучами , если смотреть прямо спереди и прямо сзади. Обнаруженные высокие и низкие частоты не были классически предсказанными значениями:
  $${\frac {f_{0}}{1-v/c}}\qquad {\text{and}}\qquad {\frac {f_{0}}{1+v/c}}$$
  Высокие и низкие частоты излучения движущихся источников измерялись как:
  $${\sqrt {\frac {1+v/c}{1-v/c}}}f_{0}=\gamma \left(1+v/c\right)f_{0}\qquad {\text{and}}\qquad {\sqrt {\frac {1-v/c}{1+v/c}}}f_{0}=\gamma \left(1-v/c\right)f_{0}\,$$
  как выведено Эйнштейном (1905) на основе преобразования Лоренца , когда источник движется медленно из-за фактора Лоренца.
• Хасселькамп, Мондри и Шарманн (1979) измерили доплеровский сдвиг от источника, движущегося под прямым углом к ​​лучу зрения. Наиболее общая связь между частотами излучения движущихся источников определяется формулой:
  $$f_{\mathrm {detected} }=f_{\mathrm {rest} }{\left(1-{\frac {v}{c}}\cos \phi \right)/{\sqrt {1-{v^{2}}/{c^{2}}}}}$$
  как установил Эйнштейн (1905). Для φ = 90° ( cos φ = 0 ) это сводится к f _{обнаружен} = f _rest γ . Эту более низкую частоту движущегося источника можно объяснить эффектом замедления времени, его часто называют поперечным эффектом Доплера и предсказывают теории относительности.
• В 2010 году замедление времени наблюдалось на скорости менее 10 метров в секунду с помощью оптических атомных часов, соединенных 75-метровым оптическим волокном.

Собственное время и диаграмма Минковского

Диаграмма Минковского и парадокс близнецов

Часы C находятся в относительном движении между двумя синхронизированными часами A и B. C встречается с A в d и B в f .

Парадокс близнецов . Один близнец должен сменить систему отсчета, что приводит к разным собственным временам на мировых линиях близнеца.

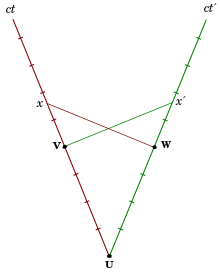
На диаграмме Минковского из первого изображения справа часы C, покоящиеся в инерциальной системе отсчета S ', встречаются с часами A в точке d и часами B в точке f (оба покоятся в S). Все три часа одновременно начинают тикать в S. Мировая линия A - это ось ct, мировая линия B, пересекающая f , параллельна оси ct, а мировая линия C - это ось ct'. Все события, одновременные с d , в S находятся на оси x, в S' - на оси x'.

Правильное время между двумя событиями указывается часами, присутствующими на обоих событиях. Оно инвариантно, т. е. во всех инерциальных системах отсчета принято, что это время указывается этими часами. Следовательно, интервал df является собственным временем часов C и короче по отношению к координатному времени ef=dg часов B и A в S. И наоборот, собственное время ef часов B короче по отношению ко времени, если в S ’, потому что событие e было измерено в S’ уже в момент i из-за относительности одновременности, задолго до того, как C начало тикать.

Из этого видно, что собственное время между двумя событиями, указываемое неускоренными часами, присутствующими при обоих событиях, по сравнению с синхронизированным координатным временем, измеренным во всех других инерциальных системах отсчета, всегда представляет собой минимальный интервал времени между этими событиями. Однако интервал между двумя событиями может соответствовать и собственному времени ускоренных часов, присутствующих при обоих событиях. При всех возможных собственных временах между двумя событиями собственное время неускоренных часов максимально , что является решением парадокса близнецов .

и

Фактор Лоренца как функция скорости (в натуральных единицах, где c = 1). Обратите внимание, что для малых скоростей (когда v стремится к нулю) γ примерно равно 1.

В дополнение к световым часам, использованным выше, формулу замедления времени можно вывести из временной части преобразования Лоренца . Пусть существуют два события, на которые движущиеся часы указывают $t_{a}$ и $t_{b}$, таким образом:

$t_{a}^{\prime }={\frac {t_{a}-{\frac {vx_{a}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},\ t_{b}^{\prime }={\frac {t_{b}-{\frac {vx_{b}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$

Поскольку часы остаются в покое в своей инерциальной системе отсчета, отсюда следует $x_{a}=x_{b}$, таким образом, интервал $\Delta t^{\prime }=t_{b}^{\prime }-t_{a}^{\prime }$ дается:

$\Delta t'=\gamma \,\Delta t={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,$

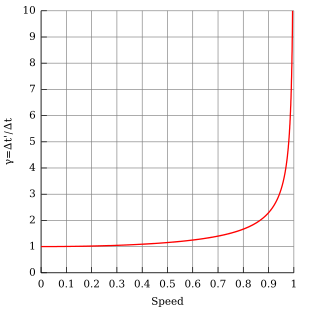
где Δ t — временной интервал между двумя однолокальными событиями (т. е. происходящими в одном и том же месте) для наблюдателя в некоторой инерциальной системе отсчета (например, тиканье его часов), известный как собственное время , Δ t’ — временной интервал между те же самые события, измеренные другим наблюдателем, движущимся по инерции со скоростью v относительно предыдущего наблюдателя, v — относительная скорость между наблюдателем и движущимися часами, c — скорость света, а фактор Лоренца (обычно обозначаемый греческая буква гамма или γ):

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,$

Таким образом, продолжительность такта движущихся часов увеличивается: измеряется, что они «идут медленно». Диапазон таких отклонений в обычной жизни, где v ≪ c , даже с учетом космических путешествий, недостаточно велик, чтобы вызвать легко обнаруживаемые эффекты замедления времени, и такие исчезающе малые эффекты можно безопасно игнорировать для большинства целей. В качестве приблизительного порога замедление времени может стать важным, когда объект приближается к скорости порядка 30 000 км/с (1/10 скорости света).

Гиперболическое движение

Основная статья: Гиперболическое движение (относительность)

В специальной теории относительности замедление времени проще всего описывается в обстоятельствах, когда относительная скорость неизменна. Тем не менее, уравнения Лоренца позволяют рассчитать собственное время и движение в пространстве для простого случая космического корабля, к которому приложена сила на единицу массы относительно некоторого эталонного объекта, находящегося в равномерном (т.е. с постоянной скоростью) движении, равном g на всем протяжении. период измерения.

Пусть t — время в инерциальной системе отсчета, впоследствии названной системой покоя. Пусть x — пространственная координата, и пусть направление постоянного ускорения, а также скорость космического корабля (относительно системы покоя) параллельны оси x . Предполагая, что положение космического корабля в момент времени t = 0 равно x = 0 , а скорость равна v ₀ , и определив следующую аббревиатуру:

$\gamma _{0}={\frac {1}{\sqrt {1-v_{0}^{2}/c^{2}}}}$

имеют место следующие формулы:

Позиция:

$x(t)={\frac {c^{2}}{g}}\left({\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}-\gamma _{0}\right)$

Скорость:

$v(t)={\frac {gt+v_{0}\gamma _{0}}{\sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}}$

Собственное время как функция координатного времени:

$\tau (t)=\tau _{0}+\int _{0}^{t}{\sqrt {1-\left({\frac {v(t')}{c}}\right)^{2}}}dt'$

В случае, когда v (0) = v ₀ = 0 и τ (0) = τ ₀ = 0, интеграл можно выразить как логарифмическую функцию или, что то же самое, как обратную гиперболическую функцию :

$\tau (t)={\frac {c}{g}}\ln \left({\frac {gt}{c}}+{\sqrt {1+\left({\frac {gt}{c}}\right)^{2}}}\right)={\frac {c}{g}}\operatorname {arsinh} \left({\frac {gt}{c}}\right)$

Как функции собственного времени $\tau$ корабля справедливы следующие формулы:

Позиция:

$x(\tau )={\frac {c^{2}}{g}}\left(\cosh {\frac {g\tau }{c}}-1\right)$

Скорость:

$v(\tau )=c\tanh {\frac {g\tau }{c}}$

Координатное время как функция собственного времени:

$t(\tau )={\frac {c}{g}}\sinh {\frac {g\tau }{c}}$

Гипотеза

Гипотеза часов — это предположение, что скорость, с которой на часы влияет замедление времени, зависит не от их ускорения, а только от их мгновенной скорости. Это эквивалентно утверждению, что часы, движущиеся по пути $P$ измеряет собственное время , определяемое:

$\tau =\int _{P}{\sqrt {dt^{2}-dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}$

Гипотеза часов была неявно (но не явно) включена в первоначальную формулировку специальной теории относительности Эйнштейна 1905 года. С тех пор оно стало стандартным предположением и обычно включается в аксиомы специальной теории относительности, особенно в свете экспериментальной проверки вплоть до очень высоких ускорений в ускорителях частиц .

вызванное гравитацией или

Основная статья: Гравитационное замедление времени

Замедление времени объясняет, почему двое работающих часов будут показывать разное время после разных ускорений. Например, на МКС время идет медленнее , отставая примерно на 0,01 секунды на каждые прошедшие 12 земных месяцев. Чтобы спутники GPS работали, они должны приспосабливаться к аналогичному искривлению пространства-времени, чтобы правильно координироваться с системами на Земле.

При удалении от центра тяжести время течет быстрее, что видно на примере массивных объектов (таких как Земля).

Гравитационное замедление времени испытывает наблюдатель, который на определенной высоте внутри гравитационной потенциальной ямы обнаруживает, что его местные часы измеряют меньше прошедшего времени, чем идентичные часы, расположенные на большей высоте (и, следовательно, имеющие более высокий гравитационный потенциал).

Гравитационное замедление времени имеет место, например, у астронавтов МКС. астронавтов В то время как относительная скорость замедляет их время, уменьшенное гравитационное влияние в месте их расположения ускоряет его, хотя и в меньшей степени. Кроме того, время альпиниста на вершине горы теоретически течет немного быстрее, чем у людей на уровне моря. Также было подсчитано, что из-за замедления времени ядро ​​Земли на 2,5 года моложе земной коры . «Часы, используемые для измерения времени полного вращения Земли, будут измерять день примерно на 10 нс/день дольше на каждый километр высоты над опорным геоидом». Путешествие в регионы космоса, где происходит экстремальное гравитационное замедление времени, например, вблизи (но не за горизонтом событий ) черной дыры , может привести к результатам сдвига во времени, аналогичным тем, которые происходят при космических путешествиях на околосветовой скорости.

В отличие от скоростного замедления времени, при котором оба наблюдателя оценивают друг друга как более медленное старение (обратный эффект), гравитационное замедление времени не является взаимным. Это означает, что при гравитационном замедлении времени оба наблюдателя согласны с тем, что часы ближе к центру гравитационного поля идут медленнее, и они согласны с соотношением разницы.

Экспериментальное тестирование

Основная статья: Экспериментальное тестирование замедления времени

• В 1959 году Роберт Паунд и Глен А. Ребка измерили очень небольшое гравитационное красное смещение частоты света, излучаемого на меньшей высоте, где гравитационное поле Земли относительно более интенсивно. Результаты оказались в пределах 10% от предсказаний общей теории относительности. В 1964 году Паунд и Дж. Л. Снайдер измерили результат в пределах 1% от значения, предсказанного гравитационным замедлением времени. (См. эксперимент Паунда – Ребки )
• В 2010 году гравитационное замедление времени было измерено на поверхности Земли при разнице высот всего в один метр с помощью оптических атомных часов.

эффект скорости и гравитационного

Суточное замедление времени (прирост или потеря, если оно отрицательное) в микросекундах как функция (кругового) радиуса орбиты r = rs / re , где rs — радиус орбиты спутника, а re — экваториальный радиус Земли, рассчитанный с использованием метрики Шварцшильда. При г ≈ 1,497 замедления времени нет. Здесь эффекты движения и пониженной гравитации компенсируются. Астронавты МКС летают внизу, тогда как GPS и геостационарные спутники летают выше.

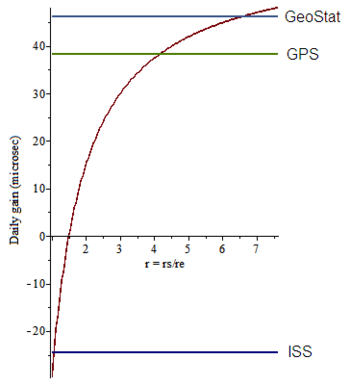
Высокоточное хронометрирование, отслеживание спутников на низкой околоземной орбите и определение времени пульсаров — это приложения, которые требуют учета комбинированных эффектов массы и движения при замедлении времени. Практические примеры включают международный стандарт атомного времени и его связь со стандартом барицентрического координатного времени, используемым для межпланетных объектов.

Эффекты релятивистского замедления времени для Солнечной системы и Земли можно очень точно смоделировать с помощью решения Шварцшильда уравнений поля Эйнштейна. В метрике Шварцшильда интервал $dt_{\text{E}}$ дается:

$dt_{\text{E}}^{2}=\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)dt_{\text{c}}^{2}-\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}}\right)^{-1}{\frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}$

где:

• $dt_{\text{E}}$ это небольшое приращение собственного времени $t_{\text{E}}$ (интервал, который можно было бы записать атомными часами),
• $dt_{\text{c}}$ это небольшое приращение координаты $t_{\text{c}}$ ( координата времени ),
• $dx,dy,dz$ небольшие приращения по трем координатам $x,y,z$ положения часов,
• ${\frac {-GM_{i}}{r_{i}}}$ представляет собой сумму ньютоновских гравитационных потенциалов, обусловленных соседними массами, исходя из их расстояний. $r_{i}$ от часов. Эта сумма включает в себя любые приливные потенциалы.

Координатная скорость часов определяется выражением:

$v^{2}={\frac {dx^{2}+dy^{2}+dz^{2}}{dt_{\text{c}}^{2}}}$

Координатное время $t_{c}$ это время, которое можно было бы отсчитывать на гипотетических «координатных часах», расположенных бесконечно далеко от всех гравитационных масс ( $U=0$), и стационарный в системе координат ( $v=0$). Точная связь между скоростью собственного времени и скоростью координатного времени для часов с радиальной составляющей скорости:

${\frac {dt_{\text{E}}}{dt_{\text{c}}}}={\sqrt {1+{\frac {2U}{c^{2}}}-{\frac {v^{2}}{c^{2}}}+\left({\frac {c^{2}}{2U}}+1\right)^{-1}{\frac {{v_{\shortparallel }}^{2}}{c^{2}}}}}={\sqrt {1-\left(\beta ^{2}+\beta _{e}^{2}+{\frac {\beta _{\shortparallel }^{2}\beta _{e}^{2}}{1-\beta _{e}^{2}}}\right)}}$

где:

• $v_{\shortparallel }$ - лучевая скорость,
• $v_{e}={\sqrt {\frac {2GM_{i}}{r_{i}}}}$ это скорость убегания,
• $\beta =v/c$, $\beta _{e}=v_{e}/c$ и $\beta _{\shortparallel }=v_{\shortparallel }/c$ скорости в процентах от скорости света c ,
• $U={\frac {-GM_{i}}{r_{i}}}$ – ньютоновский потенциал; следовательно $-U$ равна половине квадрата скорости убегания.

Приведенное выше уравнение является точным в предположениях о решении Шварцшильда. Оно сводится к уравнению скоростного замедления времени при наличии движения и отсутствии гравитации, т.е. $\beta _{e}=0$. Оно сводится к гравитационному уравнению замедления времени в отсутствие движения и наличии гравитации, т.е. $\beta =0=\beta _{\shortparallel }$.

Экспериментальное тестирование

Суточное замедление времени на высоте круговой орбиты распалось на составляющие. На этой карте только гравитационный зонд А был запущен специально для проверки общей теории относительности. Остальные космические корабли на этой схеме (за исключением МКС, диапазон точек которой помечен как «теория») оснащены атомными часами, правильная работа которых зависит от справедливости общей теории относительности.

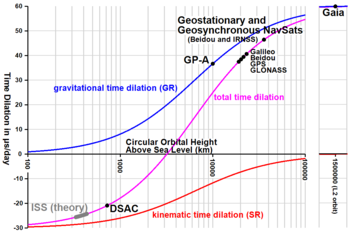
• Хафеле и Китинг в 1971 году облетели атомные часы цезия на восток и запад вокруг Земли на коммерческих авиалайнерах, чтобы сравнить прошедшее время с временем часов, которые остались в Военно-морской обсерватории США . В игру вступили два противоположных эффекта. Ожидалось, что часы стареют быстрее (показывают большее прошедшее время), чем эталонные часы, поскольку на протяжении большей части путешествия они находились в более высоком (более слабом) гравитационном потенциале (см. эксперимент Паунда-Ребки ). Но, напротив, ожидалось, что движущиеся часы стареют медленнее из-за скорости их движения. На основе фактических траекторий полета каждого полета теория предсказывала, что летающие часы по сравнению с эталонными часами в Военно-морской обсерватории США должны были терять 40 ± 23 наносекунды во время полета на восток и должны были терять 275 ± 21 наносекунду во время полета на запад. . По сравнению с атомной шкалой времени Военно-морской обсерватории США летающие часы потеряли 59 ± 10 наносекунд во время полета на восток и увеличили время на 273 ± 7 наносекунд во время полета на запад (где полосы ошибок представляют собой стандартное отклонение). В 2005 году Национальная физическая лаборатория Соединенного Королевства сообщила об ограниченном повторении этого эксперимента. Эксперимент NPL отличался от оригинала тем, что цезиевые часы были отправлены в более короткое путешествие (Лондон-Вашингтон, возвращение округа Колумбия), но часы были более точными. Сообщенные результаты находятся в пределах 4% от предсказаний теории относительности, в пределах неопределенности измерений.
• Глобальную систему позиционирования можно рассматривать как непрерывно действующий эксперимент как в специальной, так и в общей теории относительности. В орбитальные часы вносятся поправки как на специальные, так и на общие релятивистские эффекты замедления времени, как описано выше , так что (как видно с поверхности Земли) они идут с той же скоростью, что и часы на поверхности Земли.

В популярной культуре

Скорость и гравитационное замедление времени были предметом научно-фантастических произведений в различных средствах массовой информации. Некоторыми примерами в кино являются фильмы «Интерстеллар» и «Планета обезьян» . В «Интерстелларе » ключевым моментом сюжета является планета, которая находится рядом с вращающейся черной дырой и на поверхности которой один час эквивалентен семи годам на Земле из-за замедления времени. Физик Кип Торн участвовал в создании фильма и объяснил его научные концепции в книге «Наука Межзвездного пространства» .

Замедление времени использовалось в эпизодах Доктора Кто « Достаточно мира и времени » и « Доктор падает », действие которых происходит на космическом корабле вблизи черной дыры. Из-за огромного гравитационного притяжения черной дыры и длины корабля (400 миль) время на одном конце движется быстрее, чем на другом. Когда компаньона Доктора, Билла, увозят на другой конец корабля, она годами ждет, пока он ее спасет; в его время проходят лишь минуты. Более того, расширение позволяет киберлюдям развиваться «более быстрыми» темпами, чем ранее было показано в сериале.

«Тау Зеро» Роман Пола Андерсона — ранний пример этой концепции в научно-фантастической литературе. В романе космический корабль использует прямоточный воздушно-реактивный двигатель Бассарда для разгона до достаточно высоких скоростей, чтобы экипаж провел на борту пять лет, но на Земле проходит тридцать три года, прежде чем они прибудут в пункт назначения. Замедление времени со скоростью объясняется Андерсоном с точки зрения тау-фактора , который уменьшается все ближе и ближе к нулю по мере того, как корабль приближается к скорости света - отсюда и название романа. Из-за аварии экипаж не может остановить ускорение космического корабля, что приводит к такому сильному замедлению времени, что экипаж испытывает Большое сжатие в конце Вселенной. Другие примеры в литературе, такие как «Мир Роканнона» , «Гиперион» и «Вечная война» , также используют релятивистское замедление времени как научно обоснованный литературный прием, позволяющий некоторым персонажам стареть медленнее, чем остальная часть Вселенной.

См. также

• Сокращение длины
• Масса в специальной теории относительности

Дальнейшее чтение

• Каллендер, К. ; Эдни, Р. (2001). Знакомство со временем . Книги с иконками . ISBN  978-1-84046-592-1 .
• Эйнштейн, А. (1905). «К электродинамике движущихся тел» . Анналы физики . 322 (10): 891. Бибкод : 1905АнП...322..891Е . дои : 10.1002/andp.19053221004 .
• Эйнштейн, А. (1907). «О возможности новой проверки принципа относительности» . Анналы физики . 328 (6): 197–198. Бибкод : 1907АнП...328..197Е . дои : 10.1002/andp.19073280613 .
• Хасселькамп, Д.; Мондри, Э.; Шарманн, А. (1979). «Прямое наблюдение поперечного доплеровского сдвига». Журнал физики А. 289 (2): 151–155. Бибкод : 1979ZPhyA.289..151H . дои : 10.1007/BF01435932 . S2CID   120963034 .
• Айвз, HE; Стилвелл, Г. Р. (1938). «Экспериментальное исследование скорости движущихся часов». Журнал Оптического общества Америки . 28 (7): 215–226. Бибкод : 1938JOSA...28..215I . дои : 10.1364/JOSA.28.000215 .
• Айвз, HE; Стилвелл, Г. Р. (1941). «Экспериментальное исследование скорости движущихся часов. II». Журнал Оптического общества Америки . 31 (5): 369–374. Бибкод : 1941JOSA...31..369I . дои : 10.1364/JOSA.31.000369 .
• Йоос, Г. (1959). «Движущиеся системы отсчета в акустике. Эффект Доплера». Учебник теоретической физики, книга вторая (11-е изд.).
• Лармор, Дж. (1897). «К динамической теории электрической и светоносной среды» . Философские труды Королевского общества . 190 : 205–300. Бибкод : 1897RSPTA.190..205L . дои : 10.1098/rsta.1897.0020 . (третья и последняя в серии одноименных статей).
• Пуанкаре, Х. (1900). «Теория Лоренца и принцип реакции». Голландские архивы . 5 :253–78.
• Пури, А. (2015). «Эйнштейн против простой формулы маятника: замедляет ли гравитация все часы?». Физическое образование . 50 (4): 431. Бибкод : 2015PhyEd..50..431P . дои : 10.1088/0031-9120/50/4/431 . S2CID   118217730 .
• Рейнхардт, С.; и др. (2007). «Испытание релятивистского замедления времени с помощью быстрых оптических атомных часов на разных скоростях» (PDF) . Физика природы . 3 (12): 861–864. Бибкод : 2007НатФ...3..861Р . дои : 10.1038/nphys778 . Архивировано из оригинала (PDF) 12 июля 2009 г.
• Росси, Б.; Холл, Д.Б. (1941). «Изменение скорости распада мезотронов с импульсом». Физический обзор . 59 (3): 223. Бибкод : 1941PhRv...59..223R . дои : 10.1103/PhysRev.59.223 .
• Вайс, М. «Двусторонняя передача времени для спутников» . Национальный институт стандартов и технологий . Архивировано из оригинала 29 мая 2017 г.
• Фойгт, В. (1887). «О принципе Доплера». Новости Королевского общества наук в Геттингене . 2 :41-51.

Внешние ссылки

• СМИ, связанные с замедлением времени, на Викискладе?
• Меррифилд, Майкл. «Фактор Лоренца (и замедление времени)» . Шестьдесят символов . Брэди Харан из Ноттингемского университета .