Пространство-время
| Часть серии о |
| Пространство-время |
|---|
 |
В физике математическая пространство-время — это модель , которая объединяет три измерения пространства и одно измерение времени в единый четырехмерный континуум . Диаграммы пространства-времени полезны для визуализации и понимания релятивистских эффектов, например того, как разные наблюдатели воспринимают, где и когда происходят события.
До начала 20-го века предполагалось, что трехмерная геометрия Вселенной (ее описание с точки зрения местоположений, форм, расстояний и направлений) отличается от времени (измерение того, когда события происходят во Вселенной). ). Однако пространство и время приобрели новое значение благодаря преобразованию Лоренца и специальной теории относительности .
В 1908 году Герман Минковский представил геометрическую интерпретацию специальной теории относительности, которая объединила время и три пространственных измерения пространства в единый четырехмерный континуум, ныне известный как пространство Минковского . Эта интерпретация оказалась жизненно важной для общей теории относительности , согласно которой пространство-время искривляется массой и энергией .
Основы [ править ]
Определения [ править ]
Нерелятивистская классическая механика рассматривает время как универсальную величину измерения, единую во всем пространстве и отдельную от пространства. Классическая механика предполагает, что время имеет постоянную скорость, независимую от наблюдателя состояния движения или чего-либо внешнего. [1] Он предполагает, что пространство евклидово : он предполагает, что пространство следует геометрии здравого смысла. [2]
В контексте специальной теории относительности объекта время не может быть отделено от трех измерений пространства, поскольку наблюдаемая скорость течения времени для объекта зависит от скорости относительно наблюдателя. [3] : 214–217 Общая теория относительности объясняет, как гравитационные поля могут замедлять течение времени для объекта, видимого наблюдателем вне поля.
В обычном пространстве позиция задается тремя числами, известными как размеры . В декартовой системе координат они называются x, y и z. Положение в пространстве-времени называется событием и требует указания четырех чисел: трехмерного местоположения в пространстве плюс положения во времени (рис. 1). Событие представлено набором координат x , y , z и t . [4] Пространство-время, таким образом, четырехмерно .
В отличие от аналогий, используемых в популярных произведениях для объяснения таких событий, как петарды или искры, математические события имеют нулевую продолжительность и представляют собой одну точку в пространстве-времени. [5] Хотя возможно находиться в движении относительно взрыва петарды или искры, наблюдатель не может находиться в движении относительно события.
Путь частицы в пространстве-времени можно рассматривать как последовательность событий. Серия событий может быть связана вместе, чтобы сформировать линию, которая представляет продвижение частицы в пространстве-времени. частицы Эта линия называется мировой линией . [6] : 105
Математически пространство-время представляет собой многообразие , то есть оно кажется локально «плоским» вблизи каждой точки точно так же, как в достаточно малых масштабах поверхность земного шара кажется плоской. [7] Масштабный коэффициент, (обычно называемая скоростью света ) связывает расстояния, измеренные в пространстве, с расстояниями, измеренными во времени. Величина этого масштабного фактора (почти 300 000 километров или 190 000 миль в космосе эквивалентны одной секунде во времени), а также тот факт, что пространство-время представляет собой многообразие, подразумевает, что на обычных, нерелятивистских скоростях и на обычных, человеческих масштабах расстояния, мало что из того, что люди могли бы наблюдать, заметно отличалось бы от того, что они могли бы наблюдать, если бы мир был евклидовым. И только с появлением чувствительных научных измерений в середине 1800-х годов, таких как эксперимент Физо и эксперимент Майкельсона-Морли , начали отмечаться загадочные расхождения между наблюдениями и предсказаниями, основанными на неявном предположении о евклидовом пространстве. [8]

В специальной теории относительности наблюдатель в большинстве случаев будет означать систему отсчета, в которой измеряется набор объектов или событий. Такое использование существенно отличается от обычного английского значения этого термина. Системы отсчета по своей сути являются нелокальными конструкциями, и в соответствии с этим использованием этого термина не имеет смысла говорить о наблюдателе как о обладателе местоположения. [9]
На рис. 1-1 представьте себе, что рассматриваемая система отсчета оснащена плотной решеткой часов, синхронизированных внутри этой системы отсчета, которая простирается бесконечно во всех трех измерениях пространства. Какое-либо конкретное расположение внутри решетки не имеет значения. Решетка часов используется для определения времени и положения событий, происходящих в пределах всего кадра. Термин наблюдатель относится ко всему ансамблю часов, связанных с одной инерциальной системой отсчета. [9] : 17–22
В этом идеализированном случае с каждой точкой пространства связаны часы, и, таким образом, часы регистрируют каждое событие мгновенно, без временной задержки между событием и его записью. Настоящий наблюдатель увидит задержку между испусканием сигнала и его обнаружением из-за скорости света. Чтобы синхронизировать часы, при обработке данных после эксперимента время получения сигнала будет скорректировано, чтобы отразить его фактическое время, если бы оно было записано идеализированной решеткой часов. [9] : 17–22
Во многих книгах по специальной теории относительности, особенно старых, слово «наблюдатель» используется в более обычном смысле этого слова. Обычно из контекста ясно, какое значение было принято.
Физики различают то, что измеряют или наблюдают после исключения задержек распространения сигнала, и то, что можно увидеть визуально без таких поправок. Непонимание разницы между тем, что человек измеряет/наблюдает, и тем, что он видит, является источником многих ошибок среди начинающих исследователей теории относительности. [10]
История [ править ]
К середине 1800-х годов считалось, что различные эксперименты, такие как наблюдение пятна Араго и дифференциальные измерения скорости света в воздухе и воде, доказали волновую природу света в отличие от корпускулярной теории . [11] Тогда предполагалось, что распространение волн требует существования волнистой среды; в случае световых волн это считалось гипотетическим светоносным эфиром . [примечание 1] Различные попытки установить свойства этой гипотетической среды дали противоречивые результаты. Например, эксперимент Физо 1851 года, проведенный французским физиком Ипполитом Физо , продемонстрировал, что скорость света в текущей воде меньше суммы скорости света в воздухе плюс скорости воды на величину, зависящую от скорости воды. показатель преломления. [12]
Среди прочего, зависимость частичного увлечения эфира, подразумеваемая этим экспериментом, от показателя преломления (который зависит от длины волны) привела к неприятному выводу, что эфир одновременно течет с разными скоростями для разных цветов света. [13] Эксперимент Майкельсона -Морли 1887 г. (рис. 1-2) не показал дифференциального влияния движений Земли через гипотетический эфир на скорость света, а наиболее вероятное объяснение - полное увлечение эфира - противоречило наблюдению звездной аберрации. . [8]
Джордж Фрэнсис Фицджеральд в 1889 году. [14] и Хендрик Лоренц в 1892 году независимо друг от друга предположили, что материальные тела, путешествующие через неподвижный эфир, подвергаются физическому воздействию при их прохождении, сжимаясь в направлении движения на величину, которая была именно той, которая была необходима для объяснения отрицательных результатов эксперимента Майкельсона-Морли. В направлениях, поперечных направлению движения, изменений длины не происходит.
К 1904 году Лоренц расширил свою теорию настолько, что пришел к уравнениям, формально идентичным тем, которые Эйнштейн должен был вывести позже, то есть к преобразованию Лоренца . [15] Как теория динамики (изучение сил и моментов и их влияния на движение) его теория предполагала реальные физические деформации физических составляющих материи. [16] : 163–174 Уравнения Лоренца предсказали величину, которую он назвал местным временем , с помощью которой он мог объяснить аберрацию света , эксперимент Физо и другие явления.
Анри Пуанкаре был первым, кто объединил пространство и время в пространство-время. [17] [18] : 73–80, 93–95 В 1898 году он утверждал, что одновременность двух событий является вопросом условности. [19] [примечание 2] В 1900 году он признал, что «местное время» Лоренца на самом деле представляет собой то, что указывают движущиеся часы, применив явно рабочее определение синхронизации часов, предполагая постоянную скорость света. [примечание 3] В 1900 и 1904 годах он предположил присущую эфиру необнаружимость, подчеркнув обоснованность того, что он назвал принципом относительности . В 1905/1906 г. [20] он математически усовершенствовал теорию электронов Лоренца, чтобы привести ее в соответствие с постулатом относительности.
Обсуждая различные гипотезы о лоренц-инвариантной гравитации, он представил новаторскую концепцию 4-мерного пространства-времени, определив различные четыре вектора , а именно четырехпозиционный , четырехскоростной и четырехсиловый . [21] [22] Однако в последующих статьях он не стал использовать четырехмерный формализм, заявив, что это направление исследований, похоже, «влекло за собой большие страдания ради ограниченной прибыли», и в конечном итоге пришел к выводу, что «трехмерный язык кажется лучше всего подходящим для описания нашего мира». ". [22] Даже в 1909 году Пуанкаре продолжал описывать динамическую интерпретацию преобразования Лоренца. [16] : 163–174
В 1905 году Альберт Эйнштейн проанализировал специальную теорию относительности с точки зрения кинематики (исследования движущихся тел без привязки к силам), а не динамики. Его результаты были математически эквивалентны результатам Лоренца и Пуанкаре. Он получил их, признав, что вся теория может быть построена на двух постулатах: принципе относительности и принципе постоянства скорости света. Его работы были наполнены яркими образами, включающими обмен световыми сигналами между движущимися часами, тщательные измерения длин движущихся стержней и другие подобные примеры. [23] [примечание 4]
Эйнштейн в 1905 году заменил предыдущие попытки установить электромагнитное соотношение массы и энергии, введя общую эквивалентность массы и энергии , что сыграло важную роль в его последующей формулировке принципа эквивалентности в 1907 году, который провозглашал эквивалентность инерциальной и гравитационной массы. Используя эквивалентность массы и энергии, Эйнштейн показал, что гравитационная масса тела пропорциональна его энергетическому содержанию, что было одним из первых результатов в разработке общей теории относительности . Хотя может показаться, что поначалу он не мыслил геометрически о пространстве-времени, [3] : 219 В дальнейшем развитии общей теории относительности Эйнштейн полностью включил формализм пространства-времени.
Когда Эйнштейн опубликовал свою работу в 1905 году, другой из его конкурентов, его бывший профессор математики Герман Минковский , также пришел к большинству основных элементов специальной теории относительности. Макс Борн рассказал о встрече, которую он провел с Минковским, стремясь стать учеником/соавтором Минковского: [25]
Я поехал в Кельн, встретил Минковского и прослушал его знаменитую лекцию «Пространство и время», прочитанную 2 сентября 1908 года. [...] Позже он рассказал мне, что для него было большим шоком, когда Эйнштейн опубликовал свою статью, в которой эквивалентность выражено различное локальное время движения наблюдателей относительно друг друга; поскольку он пришел к тем же выводам независимо, но не опубликовал их, потому что хотел сначала разработать математическую структуру во всем ее великолепии. Он никогда не претендовал на приоритет и всегда отдавал Эйнштейну полную долю в великом открытии.
Минковский был обеспокоен состоянием электродинамики после революционных экспериментов Майкельсона, по крайней мере, с лета 1905 года, когда Минковский и Дэвид Гильберт провели продвинутый семинар, на котором присутствовали известные физики того времени, для изучения работ Лоренца, Пуанкаре и др. Минковский рассматривал работу Эйнштейна как продолжение работы Лоренца и находился под самым непосредственным влиянием Пуанкаре. [26]
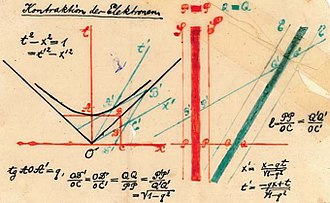
5 ноября 1907 года (немногим более чем за год до своей смерти) Минковский представил свою геометрическую интерпретацию пространства-времени в лекции Геттингенскому математическому обществу под названием « Принцип относительности» ( Das Relativitätsprinzip ). [примечание 5] 21 сентября 1908 года Минковский представил доклад « и время» Пространство . [27] в Немецкое общество ученых и врачей. Вступительные слова « Пространства и времени» включают заявление Минковского о том, что «отныне пространство для себя и время для себя полностью превратятся в простую тень, и только некоторый союз этих двух сохранит независимость». «Пространство и время» включало первое публичное представление диаграмм пространства-времени (рис. 1-4) и включало замечательную демонстрацию того, что концепция инвариантного интервала ( обсуждаемая ниже ), наряду с эмпирическим наблюдением того, что скорость света конечна, позволяет вывод всей специальной теории относительности. [примечание 6]
Понятие пространства-времени и группа Лоренца тесно связаны с некоторыми типами сферной , гиперболической или конформной геометрий и их группами преобразований, разработанными уже в XIX веке, в которых инвариантные интервалы, аналогичные пространственно-временному интервалу . используются [примечание 7]
Эйнштейн, со своей стороны, первоначально пренебрежительно относился к геометрической интерпретации специальной теории относительности Минковского, считая ее überflüssige Gelehrsamkeit (избыточной ученостью). Однако для завершения его поисков общей теории относительности, начавшихся в 1907 году, геометрическая интерпретация теории относительности оказалась жизненно важной. В 1916 году Эйнштейн полностью признал свою признательность Минковскому, интерпретация которого значительно облегчила переход к общей теории относительности. [16] : 151–152 Поскольку существуют и другие типы пространства-времени, такие как искривленное пространство-время общей теории относительности, пространство-время специальной теории относительности сегодня известно как пространство-время Минковского.
Пространство-время в специальной теории относительности [ править ]
Пространственно-временной интервал [ править ]
В трех измерениях расстояние между двумя точками можно определить с помощью теоремы Пифагора :
Хотя два зрителя могут измерить положение x , y и z двух точек, используя разные системы координат, расстояние между точками будет одинаковым для обоих, при условии, что они измеряют, используя одни и те же единицы измерения. Расстояние «инвариантно».
Однако в специальной теории относительности расстояние между двумя точками больше не одинаково, если его измеряют два разных наблюдателя, когда один из наблюдателей движется, из-за лоренцева сокращения . Ситуация еще более усложняется, если две точки разделены как во времени, так и в пространстве. Например, если один наблюдатель видит, что два события происходят в одном и том же месте, но в разное время, человек, движущийся относительно первого наблюдателя, увидит, что два события происходят в разных местах, потому что движущаяся точка зрения считает себя неподвижной. и положение события как удаляющегося или приближающегося. Таким образом, для измерения эффективного «расстояния» между двумя событиями необходимо использовать другую меру. [31] : 48–50, 100–102
В четырехмерном пространстве-времени аналогом расстояния является интервал. Хотя время является четвертым измерением, к нему относятся иначе, чем к пространственным измерениям. Таким образом, пространство Минковского во многом отличается от четырехмерного евклидова пространства . Фундаментальная причина слияния пространства и времени в пространство-время заключается в том, что пространство и время по отдельности не инвариантны, то есть при соответствующих условиях разные наблюдатели не могут прийти к единому мнению относительно продолжительности времени между двумя событиями (из-за замедления времени ) или расстояние между двумя событиями (из-за сокращения длины ). Специальная теория относительности предоставляет новый инвариант, называемый пространственно-временным интервалом , который объединяет расстояния в пространстве и во времени. Все наблюдатели, измеряющие время и расстояние между любыми двумя событиями, в конечном итоге вычислят один и тот же пространственно-временной интервал. Предположим, наблюдатель измеряет два события как разделенные во времени и пространственное расстояние Тогда квадрат пространственно-временного интервала между двумя событиями, разделенными расстоянием в космосе и в -координата: [32]
или для трёх измерений пространства,
Константа скорость света, преобразует время единицы (например, секунды) в космические единицы (например, метры). Квадрат интервала Это мера разделения между событиями A и B, которые разделены во времени и, кроме того, в пространстве, либо потому, что существуют два отдельных объекта, подвергающихся событиям, либо потому, что один объект в пространстве движется по инерции между своими событиями. Интервал разделения — это разница между квадратом пространственного расстояния, отделяющего событие B от события A, и квадратом пространственного расстояния, пройденного световым сигналом за тот же интервал времени. . Если разделение событий происходит за счет светового сигнала, то эта разница исчезает и .
Если рассматриваемые события бесконечно близки друг к другу, то можно написать
В другой инерциальной системе координат, скажем, с координатами , пространственно-временной интервал можно записать в той же форме, что и выше. Ввиду постоянства скорости света световые события во всех инерциальных системах отсчета принадлежат нулевому интервалу, . Для любого другого бесконечно малого события, когда , можно доказать, что что, в свою очередь, при интегрировании приводит к . [33] : 2 Инвариантность пространственно-временного интервала между одними и теми же событиями для всех инерциальных систем отсчета является одним из фундаментальных результатов специальной теории относительности.
Хотя для краткости часто встречаются интервальные выражения, выраженные без дельт, в том числе в большей части последующего обсуждения, следует понимать, что в целом означает и т. д. Нас всегда интересуют различия значений пространственных или временных координат, принадлежащих двум событиям, и, поскольку предпочтительного начала координат нет, отдельные значения координат не имеют существенного значения.

Приведенное выше уравнение похоже на теорему Пифагора, за исключением знака минус между и условия. Пространственно-временной интервал – это величина нет сам. Причина в том, что в отличие от расстояний в евклидовой геометрии интервалы в пространстве-времени Минковского могут быть отрицательными. Вместо того чтобы иметь дело с квадратными корнями из отрицательных чисел, физики обычно рассматривают как отдельный символ сам по себе, а не как квадрат чего-либо. [3] : 217
- Примечание. В литературе по теории относительности используются два соглашения о знаках:
- и
- Эти соглашения о знаках связаны с подписями метрики (+---) и (-+++). Незначительное изменение заключается в размещении временной координаты последней, а не первой. Оба соглашения широко используются в области исследования. [34]
- В дальнейшем обсуждении мы будем использовать первое соглашение.
В общем может принимать любое действительное числовое значение. Если положителен, пространственно-временной интервал называется времениподобным . Поскольку пространственное расстояние, пройденное любым массивным объектом, всегда меньше расстояния, проходимого светом за тот же интервал времени, положительные интервалы всегда времениподобны. Если отрицательно, то пространственно-временной интервал называется пространственноподобным . Пространственно-временные интервалы равны нулю, когда Другими словами, пространственно-временной интервал между двумя событиями на мировой линии чего-то, движущегося со скоростью света, равен нулю. Такой интервал называется светоподобным или нулевым . Фотон, попадающий в наш глаз от далекой звезды, не состарится, несмотря на то, что (с нашей точки зрения) он провел годы в пути. [31] : 48–50
Диаграмма пространства-времени обычно рисуется только с одним пространством и одной временной координатой. На рис. 2-1 представлена пространственно-временная диаграмма, иллюстрирующая мировые линии (т.е. пути в пространстве-времени) двух фотонов A и B, возникающих в результате одного и того же события и идущих в противоположных направлениях. Кроме того, C иллюстрирует мировую линию объекта, скорость которого превышает скорость света. Вертикальная координата времени масштабируется так, чтобы он имел те же единицы измерения (метры), что и горизонтальная пространственная координата. Поскольку фотоны движутся со скоростью света, их мировые линии имеют наклон ±1. [31] : 23–25 Другими словами, каждый метр, который фотон проходит влево или вправо, требует примерно 3,3 наносекунды времени.
Опорные кадры [ править ]
Этот раздел нуждается в дополнительных цитатах для проверки . ( Март 2024 г. ) |


Чтобы получить представление о том, как координаты пространства-времени, измеренные наблюдателями в разных системах отсчета, соотносятся друг с другом, полезно работать с упрощенной установкой с системами стандартной конфигурации. При осторожном подходе это позволяет упростить математические расчеты без потери общности полученных выводов. На рис. 2-2 две системы отсчета Галилея (т.е. обычные трехмерные системы координат) показаны в относительном движении. Кадр S принадлежит первому наблюдателю O, а кадр S’ (произносится как «S prime») принадлежит второму наблюдателю O’.
- Оси x , y , z кадра S ориентированы параллельно соответствующим осям со штрихом кадра S'.
- Кадр S 'движется в направлении x кадра S с постоянной скоростью v , измеренной в кадре S.
- Начало кадров S и S' совпадает, когда время t = 0 для кадра S и t ' = 0 для кадра S'. [6] : 107
Рис. 2-3a перерисовывает рис. 2-2 в другой ориентации. Рис. 2-3b иллюстрирует релятивистскую диаграмму пространства-времени с точки зрения наблюдателя O. Поскольку S и S' находятся в стандартной конфигурации, их начала совпадают в моменты времени t = 0 в системе отсчета S и t ' = 0 в системе отсчета S'. Ось ct ′ проходит через события в системе отсчета S′, у которых x ′ = 0. Но точки с x ′ = 0 движутся в x -направлении системы отсчета S со скоростью v , так что они не совпадают с ct оси в любое время, кроме нуля. Следовательно, ось ct наклонена относительно оси ct на угол θ, определяемый формулой [31] : 23–31
Ось x ' также наклонена относительно оси x . Для определения угла этого наклона напомним, что наклон мировой линии светового импульса всегда равен ±1. На рис. 2-3в представлена пространственно-временная диаграмма с точки зрения наблюдателя О'. Событие P представляет собой излучение светового импульса в точке x ′ = 0, ct ′ = − a . Импульс отражается от зеркала, расположенного на расстоянии a от источника света (событие Q), и возвращается к источнику света в точке x ′ = 0, ct ′ = a (событие R).
Те же события P, Q, R изображены на рис. 2-3b в системе наблюдателя O. Световые пути имеют наклоны = 1 и -1, так что △PQR образует прямоугольный треугольник с PQ и QR, расположенными под углом 45 градусов. к осям x и ct . Поскольку OP = OQ = OR, угол между x ′ и x также должен быть θ . [6] : 113–118
В то время как остальная система координат имеет оси пространства и времени, пересекающиеся под прямым углом, движущаяся система координат рисуется с осями, которые пересекаются под острым углом. Кадры на самом деле эквивалентны. [31] : 23–31 Асимметрия возникает из-за неизбежных искажений в том, как координаты пространства-времени могут отображаться на декартовой плоскости , и ее следует считать не более странной, чем то, как в проекции Меркатора Земли относительные размеры суши вблизи полюсов (Гренландия и Антарктида) сильно преувеличены по сравнению с массивами суши вблизи экватора.
Световой конус [ править ]

На рис. 2–4 событие O находится в начале пространственно-временной диаграммы, а две диагональные линии представляют все события, которые имеют нулевой пространственно-временной интервал по отношению к исходному событию. Эти две линии образуют то, что называется световым конусом события О, поскольку добавление второго пространственного измерения (рис. 2-5) создает видимость двух правильных круглых конусов , встречающихся своими вершинами в точке О. Один конус простирается в будущее. (t>0), другой в прошлое (t<0).

Световой (двойной) конус делит пространство-время на отдельные области относительно своей вершины. Внутренняя часть будущего светового конуса состоит из всех событий, которые отделены от вершины большим временем (временным расстоянием), чем необходимо для пересечения их пространственного расстояния со скоростью света; эти события составляют времениподобное будущее события О. Точно так же времениподобное прошлое включает внутренние события прошлого светового конуса. Таким образом, во времяподобных интервалах Δct , больше, чем Δx что делает времяподобные интервалы положительными. [3] : 220
Область вне светового конуса состоит из событий, которые отделены от события О большим пространством , чем можно пересечь со скоростью света за данное время . Эти события составляют так называемую пространственноподобную область события О, обозначенную на рис. 2-4 как «Другое место». Говорят, что события на самом световом конусе светоподобны (или отделены от нуля ) от О. Из-за неизменности пространственно-временного интервала все наблюдатели будут назначать один и тот же световой конус любому данному событию и, таким образом, согласятся на такое разделение пространства-времени. . [3] : 220
Световой конус играет важную роль в концепции причинности . Сигнал со скоростью, не превышающей скорость света, может перемещаться от положения и времени О к положению и времени D (рис. 2-4). Следовательно, событие О может оказать причинное влияние на событие D. Будущий световой конус содержит все события, на которые может оказать причинное влияние О. Аналогично, возможно, что сигнал со скоростью, не превышающей скорость света, может путешествие из положения и времени A в положение и время O. Световой конус прошлого содержит все события, которые могли оказать причинное влияние на O. Напротив, если предположить, что сигналы не могут распространяться быстрее скорости света, любое событие, такое как, например, B или C, в пространственноподобной области (в другом месте), не может ни повлиять на событие O, ни на них не может повлиять событие O, использующее такую сигнализацию. При этом предположении исключается причинно-следственная связь между событием О и любыми событиями в пространствеподобной области светового конуса. [35]
Относительность одновременности [ править ]

Все наблюдатели согласятся, что для любого данного события событие в пределах будущего светового конуса данного события происходит после данного события. Аналогично, для любого данного события событие в пределах светового конуса прошлого данного события происходит до данного события. Отношения «до и после», наблюдаемые для событий, разделенных во времени, остаются неизменными независимо от системы отсчета наблюдателя, то есть независимо от того, как наблюдатель может двигаться. Совершенно иная ситуация обстоит с событиями, разделенными пространством. Рис. 2-4 был нарисован из системы отсчета наблюдателя, движущегося с v = 0. В этой системе отсчета событие C происходит после события O, а событие B наблюдается перед событием O. [36]
В другой системе отсчета порядок этих событий, не связанных с причинно-следственной связью, может измениться на противоположный. В частности, отмечается, что если два события происходят одновременно в определенной системе отсчета, они обязательно разделены пространственноподобным интервалом и, таким образом, не связаны причинно. Наблюдение о том, что одновременность не является абсолютной, а зависит от системы отсчета наблюдателя, называется относительностью одновременности . [36]
Рис. 2-6 иллюстрирует использование пространственно-временных диаграмм при анализе относительности одновременности. События в пространстве-времени инвариантны, но системы координат трансформируются, как обсуждалось выше для рис. 2-3. Три события (A, B, C) происходят одновременно в системе отсчета наблюдателя, движущегося с v = 0. В системе отсчета наблюдателя, движущегося со скоростью v = 0,3 c , события кажутся происходящими в порядке C, B. , A. В системе отсчета наблюдателя, движущегося со скоростью v = −0,5 c , события кажутся происходящими в порядке A, B, C. Белая линия представляет собой плоскость одновременности, перемещающуюся из прошлого наблюдателя в будущее наблюдателя, выделяя происходящие на ней события. Серая область — это световой конус наблюдателя, который остается неизменным.
Пространственноподобный пространственно-временной интервал дает то же расстояние, которое наблюдатель мог бы измерить, если бы измеряемые события происходили одновременно с наблюдателем. Пространственноподобный пространственно-временной интервал, следовательно, обеспечивает меру собственного расстояния , т.е. истинное расстояние = Точно так же времяподобный пространственно-временной интервал дает ту же меру времени, которую можно было бы представить совокупным тиканием часов, движущихся вдоль данной мировой линии. Таким образом, времениподобный пространственно-временной интервал обеспечивает меру собственного времени = [3] : 220–221
Инвариантная гипербола [ править ]
Этот раздел нуждается в дополнительных цитатах для проверки . ( Март 2024 г. ) |

В евклидовом пространстве (имеющем только пространственные измерения) набор точек, равноудаленных (с использованием евклидовой метрики) от некоторой точки, образует круг (в двух измерениях) или сферу (в трех измерениях). В (1+1)-мерном пространстве-времени Минковского (имеющем одно временное и одно пространственное измерение) точки на некотором постоянном пространственно-временном интервале вдали от начала координат (с использованием метрики Минковского) образуют кривые, заданные двумя уравнениями
с некоторая положительная реальная константа. Эти уравнения описывают два семейства гипербол на диаграмме пространства-времени x – ct , которые называются инвариантными гиперболами .
На рис. 2-7а каждая пурпурная гипербола соединяет все события, имеющие некоторое фиксированное пространственно-подобное расстояние от начала координат, тогда как зеленые гиперболы соединяют события с равным временнеподобным разделением.
Пурпурные гиперболы, пересекающие ось x , представляют собой времяподобные кривые, то есть эти гиперболы представляют собой реальные пути, которые могут пройти (постоянно ускоряющиеся) частицы в пространстве-времени: между любыми двумя событиями на одной гиперболе возможна причинно-следственная связь, потому что обратная величина наклона, представляющая необходимую скорость, для всех секущих меньше, чем . С другой стороны, зеленые гиперболы, пересекающие ось ct , представляют собой пространственноподобные кривые, поскольку все интервалы вдоль этих гипербол являются пространственноподобными интервалами: между любыми двумя точками на одной из этих гипербол невозможна причинно-следственная связь, поскольку все секущие представляют скорости, большие, чем .
Рис. 2-7б отражает ситуацию в (1+2)-мерном пространстве-времени Минковского (одно временное и два пространственных измерения) с соответствующими гиперболоидами. Инвариантные гиперболы, смещенные на пространственноподобные интервалы от начала координат, порождают однолистные гиперболоиды , а инвариантные гиперболы, смещенные на времениподобные интервалы от начала координат, порождают двухлистные гиперболоиды.
(1+2)-мерная граница между пространственно- и времяподобными гиперболоидами, устанавливаемая событиями, образующими нулевой пространственно-временной интервал до начала координат, образуется путем вырождения гиперболоидов к световому конусу. В (1+1)-мерностях гиперболы вырождаются в две серые линии под углом 45°, изображенные на рис. 2-7а.
времени и сокращение Замедление длины
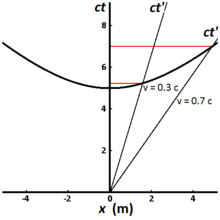
Рис. 2-8 иллюстрирует инвариантную гиперболу для всех событий, которые могут быть достигнуты от начала координат за собственное время 5 метров (приблизительно 1,67 × 10 −8 с ). Разные мировые линии представляют собой часы, движущиеся с разной скоростью. Часы, неподвижные по отношению к наблюдателю, имеют вертикальную мировую линию, а прошедшее время, измеренное наблюдателем, совпадает с собственным временем. Для часов, движущихся со скоростью 0,3 с , прошедшее время, измеренное наблюдателем, составляет 5,24 метра ( 1,75 × 10 −8 с ), а для часов, движущихся со скоростью 0,7 с , прошедшее время, измеренное наблюдателем, составляет 7,00 метра ( 2,34 × 10 −8 с ). [3] : 220–221
Это иллюстрирует явление, известное как замедление времени . Часам, которые движутся быстрее, требуется больше времени (в системе наблюдателя), чтобы отсчитывать то же количество собственного времени, и они перемещаются дальше по оси X в течение этого собственного времени, чем если бы они не имели замедления времени. [3] : 220–221 Измерение замедления времени двумя наблюдателями в разных инерциальных системах отсчета является взаимным. Если наблюдатель O измеряет, что часы наблюдателя O' идут медленнее в своей системе отсчета, наблюдатель O', в свою очередь, измеряет часы наблюдателя O' как идущие медленнее.

Сокращение длины , как и замедление времени, является проявлением относительности одновременности. Измерение длины требует измерения пространственно-временного интервала между двумя событиями, которые одновременны в одной системе отсчета. Но события, одновременные в одной системе отсчета, вообще говоря, не одновременны в других системах отсчета.
На рис. 2-9 показано движение стержня длиной 1 м, движущегося со скоростью 0,5 с вдоль оси x . Края синей полосы представляют собой мировые линии двух концов стержня. Инвариантная гипербола иллюстрирует события, отделенные от начала координат пространственноподобным интервалом в 1 м. Конечные точки O и B, измеренные при t ' = 0, являются одновременными событиями в кадре S'. Но для наблюдателя в кадре S события O и B не одновременны. Чтобы измерить длину, наблюдатель в кадре S измеряет концы стержня, проецированные на ось x вдоль их мировых линий. стержня Проекция мирового листа на ось x дает длину OC в ракурсе. [6] : 125
(не показано) Проведение вертикальной линии через A так, чтобы она пересекала ось x ', показывает, что, хотя OB укорочен с точки зрения наблюдателя O, OA аналогичным образом укорочен с точки зрения наблюдателя O'. Точно так же, как каждый наблюдатель считает, что часы другого идут медленно, каждый наблюдатель измеряет, что линейки другого сжимаются.
Что касается взаимного сокращения длины, на рис. 2-9 показано, что штрихованные и незаштрихованные рамки взаимно поворачиваются на гиперболический угол (аналог обычных углов в евклидовой геометрии). [примечание 8] Из-за этого вращения проекция измерительного стержня со штрихом на ось X без штриха сокращается, в то время как проекция метрового стержня без штриха на ось X' со штрихом также сокращается.
времени и парадокс Взаимное замедление близнецов
Взаимное замедление времени [ править ]
Взаимное замедление времени и сокращение длины обычно поражают новичков как внутренне противоречивые концепции. Если наблюдатель в системе отсчета S измеряет часы, покоящиеся в системе отсчета S', как идущие медленнее, чем его часы, в то время как S' движется со скоростью v в системе S, то принцип относительности требует, чтобы наблюдатель в системе отсчета S' аналогичным образом измерял часы в кадре S, движущиеся со скоростью − v в S', но медленнее, чем у нее. Как двое часов могут идти медленнее, чем другие, — это важный вопрос, который «затрагивает суть понимания специальной теории относительности». [3] : 198
Это кажущееся противоречие проистекает из неправильного учета различных настроек необходимых взаимосвязанных измерений. Эти настройки позволяют последовательно объяснить единственное кажущееся противоречие. Речь идет не об абстрактном тикании двух одинаковых часов, а о том, как измерить в одном кадре временное расстояние двух тиков движущихся часов. Оказывается, что во взаимном наблюдении длительности между тактами часов, каждый из которых движется в соответствующем кадре, должны участвовать разные наборы часов. Чтобы измерить в системе отсчета S длительность тика движущихся часов W' (находящихся в состоянии покоя в S'), используются два дополнительных синхронизированных часа W 1 и W 2, находящихся в состоянии покоя в двух произвольно фиксированных точках в S с пространственным расстоянием d. .
- Два события могут быть определены условием «двое часов одновременно находятся в одном месте», т.е. когда W' проходит через каждые W 1 и W 2 . Для обоих событий записываются два показания совмещенных часов. Разница двух показаний W 1 и W 2 представляет собой временное расстояние между двумя событиями в S, а их пространственное расстояние равно d . Разница двух показаний W' представляет собой временное расстояние между двумя событиями в S'. В S' эти события разделены лишь во времени, они происходят в одном и том же месте S'. Из-за инвариантности пространственно-временного интервала, охватываемого этими двумя событиями, и ненулевого пространственного разделения d в S, временное расстояние в S' должно быть меньше, чем расстояние в S: меньшее временное расстояние между двумя событиями возникает из-за показания движущихся часов W' принадлежат более медленным часам W'.
И наоборот, для оценки в системе отсчета S' временного расстояния между двумя событиями на движущихся часах W (находящихся в состоянии покоя в S) нужны двое часов, находящихся в состоянии покоя в S'.
- В этом сравнении часы W движутся со скоростью − v . Повторная запись четырех показаний событий, определяемых «двумя часами одновременно в одном месте», приводит к аналогичным временным расстояниям двух событий, теперь разделенных во времени и пространстве в S', и только разделенных во времени, но совмещенных в S. сохраняя пространственно-временной интервал неизменным, временное расстояние в S должно быть меньше, чем в S', из-за пространственного разделения событий в S': теперь часы W идут медленнее.
Необходимые записи для двух решений, с «одними движущимися часами» и «двумя часами в состоянии покоя» соответственно в S или S', включают два разных набора, каждый из которых состоит из трех часов. Поскольку в измерениях участвуют разные наборы часов, нет внутренней необходимости, чтобы измерения были взаимно «последовательными», так что, если один наблюдатель считает, что движущиеся часы идут медленно, другой наблюдатель измеряет, чтобы чьи-то часы были быстрыми. [3] : 198–199
Рис. 2-10 иллюстрирует предыдущее обсуждение взаимного замедления времени с помощью диаграмм Минковского. Верхнее изображение отражает измерения, как видно из кадра S «в состоянии покоя» с прямоугольными осями без штриха и кадра S ', «движущегося с v > 0», координируемого штрихованными наклонными осями, наклоненными вправо; на нижнем изображении показан кадр S 'находящийся в состоянии покоя со штрихованными прямоугольными координатами и кадр S, «движущийся с - v <0» с незаштрихованными наклонными осями, наклоненными влево.
Каждая линия, проведенная параллельно пространственной оси ( x , x ′), представляет собой линию одновременности. Все события на такой линии имеют одинаковое значение времени ( ct , ct ′). Аналогично, каждая линия, проведенная параллельно временной оси ( ct , ct ' ), представляет линию равных значений пространственных координат ( x , x ').
- На обоих изображениях можно обозначить начало координат O (= O ′ ) как событие, где соответствующие «движущиеся часы» совпадают с «первыми покоящимися часами» в обоих сравнениях. Очевидно, что для этого события показания на обоих часах в обоих сравнениях равны нулю. Как следствие, мировые линии движущихся часов имеют наклон вправо по оси ct (верхние изображения, часы W') и наклоненные влево по оси ct (нижние изображения, часы W). Мировые линии W 1 и W 1 представляют собой соответствующие вертикальные оси времени ( ct на верхних рисунках и ct ′ на нижних рисунках).
- На верхнем рисунке место для W 2 взято A x > 0, и таким образом мировая линия (не показанная на рисунках) этих часов пересекает мировую линию движущихся часов ( ось ct ) в событии, обозначенном A , где «двое часов одновременно находятся в одном месте». На нижнем рисунке место для W' 2 взято как C x ' < 0, и поэтому в этом измерении движущиеся часы W проходят мимо W' 2 в событии C .
- На верхнем рисунке ct -координата A t события A (показание W 2 ) обозначена B , что дает прошедшее время между двумя событиями, измеренное с помощью W 1 и W 2 , как OB . Для сравнения длину временного интервала OA , измеренную с помощью W', необходимо преобразовать в масштаб оси ct . Это делается с помощью инвариантной гиперболы (см. также рис. 2-8) через A , соединяющей все события с тем же пространственно-временным интервалом от начала координат, что A. и Это дает событие C на оси ct , и, очевидно: OC < OB , «движущиеся» часы W' работают медленнее.
Чтобы сразу показать взаимное замедление времени на верхнем рисунке, событие D можно сконструировать как событие в точке x ′ = 0 (местоположение часов W ′ в S ′), которое одновременно с событием C ( OC имеет равный пространственно-временной интервал, как ОА ) в S'. Это показывает, что временной интервал OD длиннее, чем OA , показывая, что «движущиеся» часы работают медленнее. [6] : 124
На нижнем рисунке система S движется со скоростью − v в системе S', покоящейся. Мировая линия часов W — это ось ct (наклоненная влево), мировая линия W’ 1 — это вертикальная ось ct ’, а мировая линия W’ 2 — это вертикаль, проходящая через событие C , с ct координатой ′. Д. Инвариантная гипербола через событие C масштабирует временной интервал OC до OA , который короче, чем OD ; Кроме того, B строится (аналогично D на верхних рисунках) одновременно с A в S при x = 0. Результат OB > OC снова соответствует приведенному выше.
Слово «мера» имеет важное значение. В классической физике наблюдатель не может повлиять на наблюдаемый объект, но состояние движения объекта может наблюдателем повлиять на наблюдения объекта .
Парадокс близнецов [ править ]
Многие введения в специальную теорию относительности иллюстрируют различия между теорией относительности Галилея и специальной теорией относительности, представляя ряд «парадоксов». Эти парадоксы, по сути, являются некорректными задачами, возникающими из-за нашего незнания скоростей, сравнимых со скоростью света. Лекарство состоит в том, чтобы решить многие проблемы специальной теории относительности и ознакомиться с ее так называемыми контринтуитивными предсказаниями. Геометрический подход к изучению пространства-времени считается одним из лучших методов развития современной интуиции. [37]
Парадокс близнецов — это мысленный эксперимент с участием однояйцевых близнецов, один из которых совершает путешествие в космос на высокоскоростной ракете, а вернувшись домой обнаруживает, что оставшийся на Земле близнец постарел еще сильнее. Этот результат кажется загадочным, поскольку каждый близнец наблюдает за движением другого близнеца, и поэтому на первый взгляд может показаться, что каждый из них должен обнаружить, что другой постарел меньше. Парадокс близнецов обходит оправдание взаимного замедления времени, представленное выше, избегая требования наличия третьих часов. [3] : 207 Тем не менее, парадокс близнецов не является настоящим парадоксом, поскольку его легко понять в контексте специальной теории относительности.
Впечатление о существовании парадокса возникает из-за непонимания того, что утверждает специальная теория относительности. Специальная теория относительности не объявляет эквивалентными все системы отсчета, а только инерциальные. Корпус путешествующего близнеца не является инерционным в периоды ускорения. Более того, разницу между близнецами можно обнаружить наблюдательно: путешествующему близнецу нужно запустить ракеты, чтобы иметь возможность вернуться домой, а близнецу, сидящему дома, этого не нужно. [38] [примечание 9]
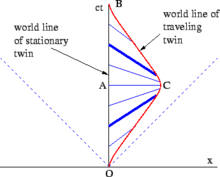
Эти различия должны привести к разнице в возрасте близнецов. Пространственно-временная диаграмма на рис. 2-11 представляет простой случай, когда близнец движется прямо вдоль оси x и тут же поворачивает обратно. С точки зрения близнеца-домохозяина, в парадоксе близнецов вообще нет ничего загадочного. Собственное время, измеренное вдоль мировой линии путешествующего близнеца от О до С, плюс собственное время, измеренное от С до В, меньше собственного времени близнеца-домохозяина, измеренного от О до А до В. Более сложные траектории требуют интегрирования собственное время между соответствующими событиями на кривой (т. е. интеграл по траектории ) для расчета общего количества собственного времени, которое испытывает путешествующий двойник. [38]
Сложности возникают, если анализировать парадокс близнецов с точки зрения путешествующего близнеца.
В дальнейшем используется номенклатура Вайса, обозначающая близнеца-домохозяина как Теренс, а путешествующего близнеца как Стеллу. [38]
Стелла не находится в инерциальной системе отсчета. Учитывая этот факт, иногда ошибочно утверждают, что для полного разрешения парадокса близнецов необходима общая теория относительности: [38]
Чистый СР-анализ будет следующим: если Стеллу анализировать в системе покоя, она неподвижна на протяжении всего путешествия. Когда она запускает ракеты для разворота, она испытывает псевдосилу, напоминающую силу гравитации. [38] Рис. 2-6 и 2-11 иллюстрируют концепцию линий (плоскостей) одновременности: Линии, параллельные оси x наблюдателя ( плоскость xy ), представляют наборы событий, которые одновременны в системе координат наблюдателя. На рис. 2-11 синие линии соединяют события на мировой линии Теренса, которые, с точки зрения Стеллы , одновременны с событиями на ее мировой линии. (Теренс, в свою очередь, будет наблюдать набор горизонтальных линий одновременности.) На протяжении как исходящего, так и обратного этапов путешествия Стеллы она считает, что часы Теренса идут медленнее, чем ее собственные. Но во время поворота (т.е. между жирными синими линиями на рисунке) происходит сдвиг угла ее линий одновременности, что соответствует быстрому пропуску событий в мировой линии Теренса, которые Стелла считает одновременными с ее собственная. Поэтому в конце путешествия Стелла обнаруживает, что Теренс постарел больше, чем она. [38]
Хотя общая теория относительности не требуется для анализа парадокса близнецов, применение принципа эквивалентности общей теории относительности дает некоторое дополнительное понимание предмета. Стелла не стационарна в инерциальной системе отсчета. Анализируя в кадре покоя Стеллы, она неподвижна на протяжении всего путешествия. Когда она движется по инерции, ее система покоя инерционна, и кажется, что часы Теренса идут медленно. Но когда она запускает ракеты для разворота, ее система покоя является ускоренной, и она испытывает силу, которая толкает ее, как если бы она находилась в гравитационном поле. Теренс окажется высоко в этом поле, и из-за гравитационного замедления времени его часы будут идти настолько быстро, что конечным результатом будет то, что Теренс постарел больше, чем Стелла, когда они снова будут вместе. [38] Теоретические аргументы, предсказывающие гравитационное замедление времени, не являются исключительными для общей теории относительности. Любая теория гравитации предсказывает гравитационное замедление времени, если она соблюдает принцип эквивалентности, включая теорию Ньютона. [3] : 16
Гравитация [ править ]
Этот вводный раздел посвящен пространству-времени специальной теории относительности, поскольку его легче всего описать. Пространство-время Минковского плоско, не учитывает гравитацию, однородно во всем и служит не чем иным, как статическим фоном для происходящих в нем событий. Наличие гравитации значительно усложняет описание пространства-времени. В общей теории относительности пространство-время больше не является статическим фоном, а активно взаимодействует с содержащимися в нем физическими системами. Пространство-время искривляется в присутствии материи, может распространять волны, преломлять свет и проявлять множество других явлений. [3] : 221 Некоторые из этих явлений описаны в последующих разделах этой статьи.
Базовая математика пространства-времени [ править ]
Преобразования Галилея [ править ]
Основная цель — иметь возможность сравнивать измерения, сделанные наблюдателями в относительном движении. Если в кадре S есть наблюдатель O, который измерил временные и пространственные координаты события, присвоив этому событию три декартовых координаты и время, измеренное на его решетке синхронизированных часов ( x , y , z , t ) (см . рис. . 1-1 ). Второй наблюдатель O' в другой системе отсчета S' измеряет то же самое событие в своей системе координат и своей решетке синхронизированных часов ( x ' , y ' , z ' , t ' ) . В инерциальных системах отсчета ни один наблюдатель не испытывает ускорения, и простая система уравнений позволяет нам связать координаты ( x , y , z , t ) с ( x ′ , y ′ , z ′ , t ′ ) . Учитывая, что две системы координат имеют стандартную конфигурацию, то есть они выровнены по параллельным ( x , y , z ) координатам и что t = 0 , когда t ′ = 0 , преобразование координат происходит следующим образом: [39] [40]
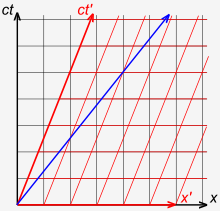
Рис. 3-1 иллюстрирует, что в теории Ньютона универсальным является время, а не скорость света. [41] : 36–37 Рассмотрим следующий мысленный эксперимент: Красная стрелка иллюстрирует поезд, который движется со скоростью 0,4° относительно платформы. В поезде пассажир стреляет пулей со скоростью 0,4 с в кадр поезда. Синяя стрелка показывает, что человек, стоящий на железнодорожных путях, измеряет пулю, летящую со скоростью 0,8 с. Это соответствует нашим наивным ожиданиям.
В более общем смысле, если предположить, что кадр S' движется со скоростью v относительно кадра S, то внутри кадра S' наблюдатель O' измеряет объект, движущийся со скоростью u ' . Скорость u относительно системы отсчета S, поскольку x = ut , x ′ = x − vt и t = t ′ , можно записать как x ′ = ut - vt = ( u - v ) t = ( u - v ) t ’ . Это приводит к тому , что u ′ = x ′ / t ′ и в конечном итоге
- или
что является общепринятым законом Галилея для сложения скоростей .
скоростей Релятивистский состав

В релятивистском пространстве-времени состав скоростей совершенно иной. Чтобы немного упростить уравнения, мы вводим общее сокращение для отношения скорости объекта относительно света:
На рис. 3-2а изображен красный поезд, который движется вперед со скоростью, заданной выражением v / c = β = s / a . Из загрунтованной рамы поезда пассажир стреляет пулей со скоростью, определяемой выражением u ′ / c = β ′ = n / m , где расстояние измеряется вдоль линии, параллельной красной оси x ′, а не параллельной оси x ′. черная ось х . Какова суммарная скорость u пули относительно платформы, показанная синей стрелкой? Обращаясь к рис. 3-2b:
- С платформы совокупная скорость пули определяется выражением u = c ( s + r )/( a + b ) .
- Два желтых треугольника подобны, потому что это прямоугольные треугольники, имеющие общий угол α . В большом желтом треугольнике соотношение s / a = v / c = β .
- Отношения соответствующих сторон двух желтых треугольников постоянны, так что r / a = b / s = n / m = β ′ . Итак, б знак равно ты ′ s / c и р знак равно ты ′ а / c .
- Подставьте выражения для b и r в выражение для u на шаге 1, чтобы получить формулу Эйнштейна для сложения скоростей: [41] : 42–48
Представленная выше релятивистская формула сложения скоростей обладает несколькими важными особенностями:
- Если u ′ и v оба очень малы по сравнению со скоростью света, то произведение vu ′ / c 2 становится исчезающе малым, а общий результат становится неотличимым от формулы Галилея (формулы Ньютона) сложения скоростей: u = u ′ + v . Формула Галилея представляет собой частный случай релятивистской формулы, применимой к низким скоростям.
- Если u ′ установлено равным c , то формула дает u = c независимо от начального значения v . Скорость света одинакова для всех наблюдателей независимо от их движения относительно источника излучения. [41] : 49
замедлении времени и сокращении длины о раз Еще
Этот раздел нуждается в дополнительных цитатах для проверки . ( Март 2024 г. ) |

Получить количественные выражения для замедления времени и сокращения длины несложно. Рис. 3-3 представляет собой составное изображение, содержащее отдельные кадры, взятые из двух предыдущих анимаций, упрощенные и переименованные для целей этого раздела.
Чтобы немного уменьшить сложность уравнений, существует множество различных сокращенных обозначений для ct :
- и являются общими.
- Также очень часто можно увидеть использование соглашения

На рис. 3-3а отрезки ОА и ОК представляют равные пространственно-временные интервалы. Замедление времени представлено соотношением OB / OK . Инвариантная гипербола имеет уравнение w = √ x 2 + к 2 где k = OK , а красная линия, представляющая мировую линию движущейся частицы, имеет уравнение w = x / β = xc / v . Немного алгебраических манипуляций дает
Выражение, включающее символ квадратного корня, очень часто встречается в теории относительности, и одно выражение, связанное с этим выражением, называется фактором Лоренца и обозначается греческой буквой гамма. : [42]
Если v больше или равно c , выражение для становится физически бессмысленным, подразумевая, что c — максимально возможная скорость в природе. Для любого v, большего нуля, фактор Лоренца будет больше единицы, хотя форма кривой такова, что для малых скоростей фактор Лоренца чрезвычайно близок к единице.
На рис. 3-3б отрезки ОА и ОК представляют равные пространственно-временные интервалы. Сокращение длины представлено соотношением OB / OK . Инвариантная гипербола имеет уравнение x = √ w 2 + к 2 , где k = OK , а края синей полосы, представляющей мировые линии концов движущегося стержня, имеют наклон 1/ β = c / v . Событие А имеет координаты( Икс , ш ) знак равно ( γk , γβk ). Поскольку касательная линия, проходящая через A и B, имеет уравнение w = ( x − OB )/ β , мы имеем γβk = ( γk − OB )/ β и
Преобразования Лоренца [ править ]
Преобразования Галилея и вытекающий из них закон сложения скоростей хорошо работают в нашем обычном низкоскоростном мире самолетов, автомобилей и мячей. Однако начиная с середины 1800-х годов чувствительные научные приборы начали обнаруживать аномалии, которые плохо сочетались с обычным сложением скоростей.
Преобразования Лоренца используются для преобразования координат события из одного кадра в другой в специальной теории относительности.
Фактор Лоренца появляется в преобразованиях Лоренца:
Обратные преобразования Лоренца:
Когда v ≪ c и x достаточно мало, v 2 / с 2 и vx / c 2 члены стремятся к нулю, а преобразования Лоренца приближаются к преобразованиям Галилея.
и т. д., чаще всего действительно имеют в виду и т. д. Хотя для краткости уравнения преобразования Лоренца записаны без дельт, x означает Δ x и т. д. В общем, нас всегда интересуют различия в пространстве и времени между событиями.
Называть один набор преобразований нормальными преобразованиями Лоренца, а другой — обратными преобразованиями, вводит в заблуждение, поскольку между кадрами нет существенной разницы. Разные авторы называют тот или иной набор преобразований «обратным». Прямые и обратные преобразования тривиально связаны друг с другом, поскольку кадр S может двигаться только вперед или назад относительно S ′ . Таким образом, обращение уравнений просто влечет за собой замену переменных со штрихом и без штриха и замену v на − v . [43] : 71–79
Пример: Теренс и Стелла участвуют в космической гонке Земля-Марс. Теренс — судья на старте, а Стелла — участник. В момент времени t = t ′ = 0 космический корабль Стеллы мгновенно разгоняется до скорости 0,5 c . Расстояние от Земли до Марса составляет 300 световых секунд (около 90,0 × 10 6 км ). Теренс наблюдает, как Стелла пересекает финишную черту в момент t = 600,00 с . Но Стелла замечает, что время на ее корабельном хронометре Когда она пересекает финишную черту, она вычисляет расстояние между стартовой и финишной линиями, измеренное в ее кадре, равным 259,81 световой секунды (около 77,9 × 10 6 км ). 1).
Вывод преобразований Лоренца [ править ]
было сделано много десятков выводов преобразований Лоренца Со времени оригинальной работы Эйнштейна в 1905 году , каждый из которых имел свою конкретную направленность. Хотя вывод Эйнштейна был основан на инвариантности скорости света, существуют и другие физические принципы, которые могут служить отправной точкой. В конечном счете, эти альтернативные отправные точки можно считать различными выражениями основного принципа локальности , который гласит, что влияние, которое одна частица оказывает на другую, не может передаваться мгновенно. [44]
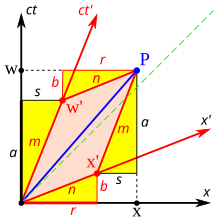
Вывод, приведенный здесь и проиллюстрированный на рис. 3-5, основан на выводе, представленном Байсом. [41] : 64–66 и использует предыдущие результаты из разделов «Релятивистская композиция скоростей», «Замедление времени» и «Сокращение длины». Событие P имеет координаты ( w , x ) в черной «системе покоя» и координаты ( w ′ , x ′ ) в красной рамке, которая движется с параметром скорости β = v / c . Чтобы определить w ′ и x ′ через w и x (или наоборот), проще сначала получить обратное преобразование Лоренца.
- Не может быть такого понятия, как расширение/сужение длины в поперечных направлениях. y ' должен равняться y, а z ' должен равняться z , в противном случае от наблюдателя будет зависеть, сможет ли быстро движущийся шар длиной 1 м пройти через круглое отверстие диаметром 1 м. Первый постулат относительности гласит, что все инерциальные системы отсчета эквивалентны, и поперечное расширение/сжатие нарушает этот закон. [43] : 27–28
- Судя по рисунку, w = a + b и x = r + s.
- Из предыдущих результатов с использованием подобных треугольников мы знаем, что s / a = b / r = v / c = β .
- Из-за замедления времени a = γw ′
- Подстановка уравнения (4) в s / a = β дает s = γw ′ β .
- Сокращение длины и подобные треугольники дают нам r = γx ′ и b = βr = βγx ′
- Подстановка выражений для s , a , r и b в уравнения на шаге 2 сразу дает
Вышеупомянутые уравнения являются альтернативными выражениями для уравнений t и x обратного преобразования Лоренца, как можно увидеть, подставив ct вместо w , ct ′ вместо w ′ и v / c вместо β . Из обратного преобразования уравнения прямого преобразования могут быть получены путем решения для t ′ и x ′ .
Линейность преобразований Лоренца [ править ]
Преобразования Лоренца обладают математическим свойством, называемым линейностью, поскольку x ′ и t ′ получаются как линейные комбинации x и t без участия высших степеней. Линейность преобразования отражает фундаментальное свойство пространства-времени, которое молчаливо предполагалось при выводе, а именно, что свойства инерциальных систем отсчета не зависят от местоположения и времени. В отсутствие гравитации пространство-время везде выглядит одинаково. [41] : 67 Все инерционные наблюдатели согласятся с тем, что представляет собой ускоряющееся и неускоряющееся движение. [43] : 72–73 Любой наблюдатель может использовать свои собственные измерения пространства и времени, но в них нет ничего абсолютного. Соглашения другого наблюдателя тоже подойдут. [3] : 190
Результатом линейности является то, что если два преобразования Лоренца применяются последовательно, результат также является преобразованием Лоренца.
Пример: Теренс наблюдает, как Стелла удаляется от него со скоростью 0,500 c , и он может использовать преобразования Лоренца с β = 0,500 , чтобы связать измерения Стеллы со своими собственными. Стелла в своей системе координат наблюдает, как Урсула удаляется от нее со скоростью 0,250 °С , и она может использовать преобразования Лоренца с β = 0,250, чтобы связать измерения Урсулы со своими собственными. Из-за линейности преобразований и релятивистского состава скоростей Теренс может использовать преобразования Лоренца с β = 0,666 , чтобы связать измерения Урсулы со своими собственными.
Эффект Доплера [ править ]
Эффект Доплера — это изменение частоты или длины волны для приемника и источника при относительном движении. Для простоты рассмотрим здесь два основных сценария: (1) движения источника и/или приемника происходят точно вдоль соединяющей их линии (продольный эффект Доплера) и (2) движения происходят под прямым углом к указанной линии ( поперечный эффект Доплера ). Мы игнорируем сценарии, в которых они движутся по промежуточным углам.
Продольный эффект Доплера [ править ]
Классический доплеровский анализ имеет дело с волнами, распространяющимися в среде, такими как звуковые волны или водная рябь, и которые передаются между источниками и приемниками, которые движутся навстречу друг другу или от них. Анализ таких волн зависит от того, движутся ли источник, приемник или оба относительно среды. Учитывая сценарий, в котором приемник неподвижен по отношению к среде, а источник движется прямо от приемника со скоростью v s для параметра скорости β s , длина волны увеличивается, и наблюдаемая частота f задается к
С другой стороны, при условии, что источник неподвижен, а приемник движется прямо от источника со скоростью v r для параметра скорости β r , длина волны не изменяется, но скорость передачи волн относительно приемника уменьшается, а наблюдаемая частота f определяется выражением
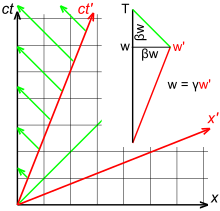
Свет, в отличие от звука или водной ряби, не распространяется через среду, и нет различия между источником, удаляющимся от приемника, и приемником, удаляющимся от источника. На рис. 3-6 показана релятивистская пространственно-временная диаграмма, показывающая источник, отделяющийся от приемника с параметром скорости. так, чтобы расстояние между источником и приемником во времени является . Из-за замедления времени, Поскольку наклон луча зеленого света равен -1, Следовательно, релятивистский эффект Доплера определяется выражением [41] : 58–59
Поперечный эффект Доплера [ править ]
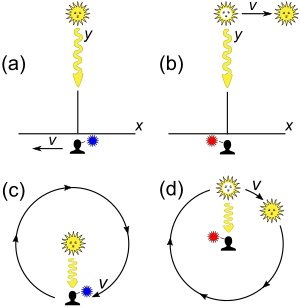
Предположим, что источник и приемник, приближающиеся друг к другу по равномерному инерционному движению вдоль непересекающихся линий, находятся на максимальном сближении друг с другом. Казалось бы, классический анализ предсказывает, что приемник не обнаружит доплеровского сдвига. Из-за тонкостей анализа это ожидание не обязательно соответствует действительности. Тем не менее, при правильном определении поперечный доплеровский сдвиг представляет собой релятивистский эффект, не имеющий классического аналога. Тонкости такие: [45] : 541–543
- Рис. 3-7а. Как измеряется частота, когда приемник геометрически максимально приближен к источнику? Этот сценарий легче всего анализировать по кадру S' источника. [примечание 10]
- Рис. 3-7б. Как измеряется частота, когда приемник видит источник как ближайший к нему? Этот сценарий легче всего анализировать по кадру S приемника.
При обсуждении поперечного доплеровского сдвига обычно рассматриваются два других сценария:
- Рис. 3-7в. Какую частоту измеряет приемник, если приемник движется по кругу вокруг источника?
- Рис. 3-7г. Если источник движется по кругу вокруг приемника, какую частоту измеряет приемник?
В сценарии (a) точка наибольшего сближения не зависит от кадра и представляет собой момент, когда нет изменения расстояния во времени (т. е. dr/dt = 0, где r — расстояние между приемником и источником) и, следовательно, нет продольного доплеровского эффекта. сдвиг. Источник наблюдает, что приемник освещен светом частоты f ′ , но также наблюдает, что приемник имеет часы с замедленным временем. Таким образом, в кадре S приемник освещается синесмещенным светом с частотой
В сценарии (b) на рисунке показано, как приемник освещается светом, когда источник находился ближе всего к приемнику, даже если источник переместился дальше. Поскольку часы источника замедлены во времени, как измерено в кадре S, и поскольку в этой точке dr/dt было равно нулю, свет от источника, излучаемый из этой ближайшей точки, смещается в красную сторону с частотой
Сценарии (c) и (d) можно проанализировать с помощью простых аргументов в пользу замедления времени. В (c) приемник наблюдает свет от источника как сдвинутый в голубую сторону в раз. , а в (d) свет смещен в красную сторону. Единственная кажущаяся сложность заключается в том, что орбитальные объекты находятся в ускоренном движении. Однако, если инерционный наблюдатель смотрит на ускоряющиеся часы, при вычислении замедления времени важна только мгновенная скорость часов. (Обратное, однако, неверно.) [45] : 541–543 В большинстве сообщений о поперечном доплеровском сдвиге этот эффект называется красным смещением и анализируется с точки зрения сценариев (b) или (d). [примечание 11]
Энергия и импульс [ править ]
импульса на измерения Распространение четыре

В классической механике состояние движения частицы характеризуется ее массой и скоростью. Линейный импульс , произведение массы частицы на скорость, представляет собой векторную величину, имеющую то же направление, что и скорость: p = m v . Это сохраняющаяся величина, означающая, что если на закрытую систему не действуют внешние силы, ее полный линейный импульс не может измениться.
В релятивистской механике вектор импульса расширен до четырех измерений. К вектору импульса добавляется временной компонент, который позволяет вектору импульса пространства-времени трансформироваться подобно вектору положения пространства-времени. . Исследуя свойства импульса пространства-времени, мы начнем (рис. 3-8а) с рассмотрения того, как выглядит частица в состоянии покоя. В остальной системе отсчета пространственная составляющая импульса равна нулю, т.е. p = 0 , а временная составляющая равна mc .
Мы можем получить преобразованные компоненты этого вектора в движущейся системе отсчета, используя преобразования Лоренца, или можем прочитать их непосредственно с рисунка, поскольку мы знаем, что и , поскольку красные оси масштабируются по гамме. Рис. 3-8b иллюстрирует ситуацию в движущемся кадре. Очевидно, что пространственная и временная компоненты четырехимпульса стремятся к бесконечности, когда скорость движущейся системы приближается к c . [41] : 84–87
Вскоре мы воспользуемся этой информацией, чтобы получить выражение для четырехимпульса .
Импульс света [ править ]
Частицы света, или фотоны, движутся со скоростью c , константой, которую обычно называют скоростью света . Это утверждение не является тавтологией, поскольку многие современные формулировки теории относительности не исходят из постулата постоянной скорости света. Таким образом, фотоны распространяются вдоль светоподобной мировой линии и в соответствующих единицах имеют равные пространственные и временные компоненты для каждого наблюдателя.
Следствием теории электромагнетизма Максвелла является то, что свет несет энергию и импульс, и что их соотношение является постоянным: . Перестановка, , и поскольку для фотонов пространственная и временная компоненты равны, E/c поэтому должно быть приравнено к временной составляющей вектора импульса пространства-времени.
Фотоны движутся со скоростью света, но имеют конечный импульс и энергию. Чтобы это было так, массовый член в γmc должен быть равен нулю, а это означает, что фотоны являются безмассовыми частицами . Бесконечность, умноженная на ноль, — плохо определенная величина, но E/c определена четко.
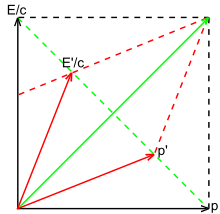
Согласно этому анализу, если энергия фотона равна E в системе покоя, она равна в движущемся кадре. Этот результат может быть получен путем рассмотрения рис. 3-9 или путем применения преобразований Лоренца и согласуется с анализом эффекта Доплера, приведенным ранее. [41] : 88
Отношения масса-энергия [ править ]
Рассмотрение взаимосвязей между различными компонентами релятивистского вектора импульса привело Эйнштейна к нескольким важным выводам.
- В пределе низкой скорости, когда β = v / c приближается к нулю, γ приближается к 1, поэтому пространственная составляющая релятивистского импульса приближается к mv , классическому термину для импульса. Следуя этой точке зрения, γm можно интерпретировать как релятивистское обобщение m . Эйнштейн предположил, что релятивистская масса объекта увеличивается со скоростью по формуле .
- Аналогично, сравнивая временную составляющую релятивистского импульса с временной составляющей фотона: , так что Эйнштейн пришел к соотношению . Упрощенно до случая нулевой скорости это уравнение Эйнштейна, связывающее энергию и массу.
Другой способ взглянуть на взаимосвязь между массой и энергией — рассмотреть разложение γmc в ряд. 2 на низкой скорости:
Второе слагаемое представляет собой просто выражение кинетической энергии частицы. Действительно, масса является еще одной формой энергии. [41] : 90–92 [43] : 129–130, 180
Концепция релятивистской массы, введенная Эйнштейном в 1905 году, m rel , хотя и тщательно подтверждается каждый день в ускорителях частиц по всему миру (да и вообще в любых приборах, использование которых зависит от частиц с высокой скоростью, таких как электронные микроскопы, [46] старомодные цветные телевизоры и т. д.), тем не менее, не оказалась плодотворной концепцией в физике в том смысле, что она не послужила основой для других теоретических разработок. Например, релятивистская масса не играет никакой роли в общей теории относительности.
По этой причине, а также по педагогическим соображениям, большинство физиков в настоящее время предпочитают другую терминологию, говоря о взаимосвязи между массой и энергией. [47] «Релятивистская масса» — устаревший термин. Термин «масса» сам по себе относится к массе покоя или инвариантной массе и равен инвариантной длине вектора релятивистского импульса. Выраженный в виде формулы,
Эта формула применима ко всем частицам, как безмассовым, так и массивным. Для фотонов, где m rest равно нулю, это дает: . [41] : 90–92
Четырехимпульс [ править ]
Из-за тесной связи между массой и энергией четырехимпульс (также называемый 4-импульсом) также называют 4-вектором энергии-импульса. Используя прописную букву P для обозначения четырехимпульса и строчную букву p для обозначения пространственного импульса, четырехимпульс можно записать как
- или альтернативно,
- используя соглашение, которое [43] : 129–130, 180
Законы сохранения [ править ]
В физике законы сохранения утверждают, что некоторые конкретные измеримые свойства изолированной физической системы не меняются по мере того, как система развивается с течением времени. В 1915 году Эмми Нётер обнаружила, что в основе каждого закона сохранения лежит фундаментальная симметрия природы. [48] Тот факт, что физические процессы не заботятся о том, где в пространстве они происходят ( симметрия пространственного перемещения ), приводит к сохранению импульса , тот факт, что такие процессы не заботятся о том, когда они происходят ( симметрия перемещения во времени ), приводит к сохранению энергии , и, таким образом, на. В этом разделе мы исследуем ньютоновские взгляды на сохранение массы, импульса и энергии с релятивистской точки зрения.
Общий импульс [ править ]
Чтобы понять, как ньютоновский взгляд на сохранение импульса необходимо изменить в релятивистском контексте, мы исследуем проблему двух сталкивающихся тел, ограниченных одним измерением.
В ньютоновской механике можно выделить два крайних случая этой проблемы, дающих математику минимальной сложности:
- (1) Два тела отскакивают друг от друга при полностью упругом столкновении.
- (2) Два тела слипаются и продолжают двигаться как одна частица. Второй случай представляет собой случай совершенно неупругого удара.
В обоих случаях (1) и (2) сохраняются импульс, масса и полная энергия. Однако при неупругом столкновении кинетическая энергия не сохраняется. Определенная часть начальной кинетической энергии преобразуется в тепло.
В случае (2) две массы с импульсами и сталкиваются, образуя единственную частицу сохраняющейся массы. путешествуя со скоростью центра масс исходной системы, . Общий импульс сохраняется.
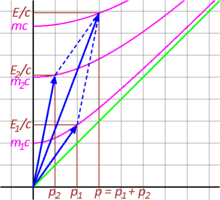
Рис. 3-10 иллюстрирует неупругое столкновение двух частиц с релятивистской точки зрения. Компоненты времени и добавьте к общему E/c результирующего вектора, что означает, что энергия сохраняется. Аналогично, космические компоненты и сложите, чтобы сформировать p результирующего вектора. Четырехимпульс, как и ожидалось, является сохраняющейся величиной. Однако инвариантная масса слившейся частицы, определяемая точкой, где инвариантная гипербола полного импульса пересекает ось энергии, не равна сумме инвариантных масс отдельных столкнувшихся частиц. Действительно, она больше суммы отдельных масс: . [41] : 94–97
Глядя на события этого сценария в обратной последовательности, мы видим, что несохранение массы — обычное явление: когда нестабильная элементарная частица спонтанно распадается на две более легкие частицы, полная энергия сохраняется, а масса — нет. Часть массы преобразуется в кинетическую энергию. [43] : 134–138
Выбор опорных систем [ править ]
Этот раздел нуждается в дополнительных цитатах для проверки . ( Март 2024 г. ) |
Свобода выбора любой структуры для проведения анализа позволяет нам выбрать ту, которая может оказаться особенно удобной. Для анализа проблем импульса и энергии наиболее удобной системой координат обычно является « система центра импульса » (также называемая системой нулевого импульса или COM-система). Это система отсчета, в которой пространственная составляющая полного импульса системы равна нулю. Рис. 3-11 иллюстрирует распад высокоскоростной частицы на две дочерние частицы. В лабораторных условиях дочерние частицы преимущественно испускаются в направлении, ориентированном вдоль траектории исходной частицы. Однако в системе COM две дочерние частицы испускаются в противоположных направлениях, хотя их массы и величины скоростей обычно не одинаковы.
Сохранение энергии и импульса [ править ]
В ньютоновском анализе взаимодействующих частиц преобразование между системами отсчета является простым, поскольку все, что необходимо, — это применить преобразование Галилея ко всем скоростям. С , импульс . Если наблюдается сохранение полного импульса взаимодействующей системы частиц в одной системе отсчета, то точно так же будет наблюдаться его сохранение и в любой другой системе отсчета. [43] : 241–245
Сохранение импульса в системе отсчета COM сводится к требованию, чтобы p = 0 как до, так и после столкновения. В ньютоновском анализе сохранение массы диктует, что . В упрощенных одномерных сценариях, которые мы рассматривали, необходимо только одно дополнительное ограничение, прежде чем можно будет определить исходящие импульсы частиц — энергетическое условие. В одномерном случае полностью упругого столкновения без потери кинетической энергии исходящие скорости отскакивающих частиц в системе COM будут точно равны и противоположны их скоростям прилета. В случае совершенно неупругого столкновения с полной потерей кинетической энергии скорости вылета отскакивающих частиц будут равны нулю. [43] : 241–245
Ньютоновские импульсы, рассчитанные как , не ведут себя должным образом при лоренцевом преобразовании. Линейное преобразование скоростей заменяется сильно нелинейным так что расчет, демонстрирующий сохранение импульса в одном кадре, будет недействителен в других кадрах. Эйнштейн столкнулся с необходимостью либо отказаться от сохранения импульса, либо изменить определение импульса. Он выбрал именно этот второй вариант. [41] : 104
Релятивистский закон сохранения энергии и импульса заменяет три классических закона сохранения энергии, импульса и массы. Масса больше не сохраняется независимо, поскольку она включена в полную релятивистскую энергию. Это делает релятивистское сохранение энергии более простой концепцией, чем в нерелятивистской механике, поскольку полная энергия сохраняется без каких-либо оговорок. Кинетическая энергия, преобразованная в тепло или внутреннюю потенциальную энергию, проявляется в увеличении массы. [43] : 127
Рис. 3-12а иллюстрирует диаграмму энергии-импульса для этой реакции распада в системе покоя пиона. Из-за своей незначительной массы нейтрино движется со скоростью, близкой к скорости света. Релятивистское выражение для его энергии, как и у фотона, имеет вид что также является значением пространственной составляющей его импульса. Для сохранения импульса мюон имеет то же значение пространственной составляющей импульса нейтрино, но в противоположном направлении.
Алгебраический анализ энергетики этой реакции распада доступен в Интернете. [49] поэтому на рис. 3-12b вместо этого представлено решение графического калькулятора. Энергия нейтрино 29,79 МэВ, а энергия мюона 33,91 МэВ − 29,79 МэВ = 4,12 МэВ . Большую часть энергии уносит нейтрино с массой, близкой к нулевой.За пределами основ [ править ]
Темы этого раздела имеют значительно большую техническую сложность, чем темы предыдущих разделов, и не являются существенными для понимания « Введения в искривленное пространство-время».
Быстрота [ править ]
Преобразования Лоренца связывают координаты событий в одной системе отсчета с событиями в другой системе отсчета. Релятивистская композиция скоростей используется для сложения двух скоростей. Формулы для выполнения последних вычислений нелинейны, что делает их более сложными, чем соответствующие формулы Галилея.
Эта нелинейность является результатом нашего выбора параметров. [9] : 47–59 Ранее мы отмечали, что на пространственно-временной диаграмме x – ct точки, находящиеся на некотором постоянном пространственно-временном интервале от начала координат, образуют инвариантную гиперболу. Мы также отметили, что системы координат двух пространственно-временных систем отсчета в стандартной конфигурации гиперболически повернуты относительно друг друга.
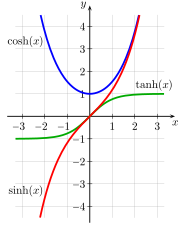
Естественными функциями для выражения этих соотношений являются гиперболические аналоги тригонометрических функций . На рис. 4-1а показан единичный круг с sin( a ) и cos( a ), единственное отличие этой диаграммы от знакомого единичного круга элементарной тригонометрии состоит в том, что a интерпретируется, а не как угол между лучом и x. -ось , а как удвоенная площадь сектора, выметаемого лучом от x оси . Численно угол и 2×площадь единичного круга идентичны. На рис. 4-1b показана единичная гипербола с sinh( a ) и cosh( a ), где a также интерпретируется как удвоенная окрашенная область. [50] На рис. 4-2 представлены графики функций sinh, cosh и tanh.
Для единичного круга наклон луча определяется выражением
В декартовой плоскости поворот точки ( x , y ) в точку ( x ' , y ' ) на угол θ определяется выражением
На пространственно-временной диаграмме параметр скорости является аналогом наклона. Быстрота φ выражением определяется [43] : 96–99
где
Определенная выше быстрота очень полезна в специальной теории относительности, поскольку многие выражения принимают значительно более простую форму, когда выражаются через нее. Например, в формуле коллинеарного сложения скорости скорость просто складывается; [9] : 47–59
или другими словами,
Преобразования Лоренца принимают простую форму, если выражать их через быстроту. Фактор γ можно записать как
Преобразования, описывающие относительное движение с равномерной скоростью и без вращения осей пространственных координат, называются бустами .
Подставив γ и γβ в преобразования, представленные ранее, и переписав их в матричной форме, усиление Лоренца в x направлении можно записать как
а обратное усиление Лоренца в x направлении можно записать как
Другими словами, повышения Лоренца представляют собой гиперболические вращения в пространстве-времени Минковского. [43] : 96–99
Преимущества использования гиперболических функций таковы, что некоторые учебники, такие как классические учебники Тейлора и Уиллера, знакомят с их использованием на очень ранней стадии. [9] [51] [примечание 12]
4‑вектора [ править ]
Четыре-вектора были упомянуты выше в контексте 4-вектора энергии-импульса , но без особого акцента. Действительно, ни один из элементарных выводов специальной теории относительности не требует их. Но как только они будут поняты, 4-векторы и, в более общем смысле, тензоры , значительно упрощают математику и концептуальное понимание специальной теории относительности. Работа исключительно с такими объектами приводит к формулам, явно релятивистски инвариантным, что является значительным преимуществом в нетривиальных контекстах. Например, демонстрация релятивистской инвариантности уравнений Максвелла в их обычной форме не является тривиальной, хотя это всего лишь рутинное вычисление, на самом деле не более чем наблюдение, с использованием формулировки тензора напряженности поля . [52]
С другой стороны, общая теория относительности с самого начала в значительной степени опирается на 4-векторы и, в более общем смысле, на тензоры, представляющие физически значимые объекты. Чтобы связать их посредством уравнений, которые не опираются на конкретные координаты, необходимы тензоры, способные соединить такие 4-вектора даже в искривленном пространстве-времени, а не только в плоском , как в специальной теории относительности. Изучение тензоров выходит за рамки этой статьи, в которой представлено лишь базовое обсуждение пространства-времени.
Определение 4-векторов [ править ]
4-х кортеж, является «4-вектором», если его компонент A i преобразуется между кадрами согласно преобразованию Лоренца.
Если вы используете координатах A является 4-вектором , если он преобразуется (в x направлении ) по закону
который получается в результате простой замены ct на A 0 и x на A 1 в предыдущем представлении преобразования Лоренца.
Как обычно, когда мы пишем x , t и т. д., мы обычно имеем в виду Δx , Δt и т. д.
Последние три компонента 4-вектора должны быть стандартным вектором в трехмерном пространстве. Следовательно, 4–вектор должен преобразоваться как при преобразованиях Лоренца, а также при вращениях. [37] : 36–59
Свойства 4-векторов [ править ]
- Замыкание при линейной комбинации: если A и B — 4-векторы , то также является 4-вектором .
- Инвариантность внутреннего продукта: если A и B являются 4-векторами , то их внутренний продукт (скалярный продукт) инвариантен, т.е. их внутренний продукт не зависит от системы отсчета, в которой он вычисляется. Обратите внимание, чем вычисление внутреннего продукта отличается от вычисления внутреннего продукта 3-вектора . В дальнейшем и являются 3-векторами :
- Помимо того, что указанный выше внутренний продукт инвариантен относительно преобразования Лоренца, он также инвариантен относительно вращения в трехмерном пространстве .
- Два вектора называются ортогональными, если В отличие от случая с 3-векторами, ортогональные 4-векторы не обязательно находятся под прямым углом друг к другу. Правило состоит в том, что два 4-вектора ортогональны, если они смещены на равные и противоположные углы от линии 45 °, которая является мировой линией светового луча. Это означает, что светоподобный 4-вектор ортогонален сам себе .
- Инвариантность величины вектора. Величина вектора является внутренним произведением 4-вектора на самого себя и является свойством, не зависящим от системы координат. Как и в случае с интервалами, величина может быть положительной, отрицательной или нулевой, поэтому векторы называются времениподобными, пространственноподобными или нулевыми (светоподобными). Обратите внимание, что нулевой вектор — это не то же самое, что нулевой вектор. Нулевой вектор – это такой вектор, для которого а нулевой вектор — это вектор, все компоненты которого равны нулю. К частным случаям, иллюстрирующим неизменность нормы, относится инвариантный интервал и инвариантная длина вектора релятивистского импульса [43] : 178–181 [37] : 36–59
Примеры 4-векторов [ править ]
- 4-вектор смещения: иначе известный как разделение пространства-времени , это ( Δt, Δx, Δy, Δz ) или для бесконечно малых разделений ( dt, dx, dy, dz ) .
- 4-вектор скорости: получается, когда 4-вектор смещения делится на , где — это правильное время между двумя событиями, которые дают dt, dx, dy и dz .
- касается 4-скорость мировой линии частицы и имеет длину, равную одной единице времени в системе отсчёта частицы.
- Ускоренная частица не имеет инерциальной системы отсчета, в которой она всегда покоится. Однако всегда можно найти инерциальную систему отсчета, которая в данный момент движется вместе с частицей. Эта система отсчёта, мгновенно движущаяся система отсчёта (MCRF), позволяет применять специальную теорию относительности к анализу ускоренных частиц.
- Поскольку фотоны движутся по нулевым линиям, для фотона и 4-скорость определить невозможно. Не существует системы отсчета, в которой фотон покоится, и на пути фотона не может быть установлена MCRF.
- Энергия-импульс 4-вектора:
- Как указывалось ранее, существуют различные трактовки 4-вектора энергии-импульса , так что его также можно увидеть выраженным как или Первая компонента — это полная энергия (включая массу) частицы (или системы частиц) в данной системе отсчета, а остальные компоненты — ее пространственный импульс. энергии-импульса 4-вектор является сохраняющейся величиной.
- 4-вектор ускорения: получается в результате взятия производной 4-вектора скорости по
- 4-вектор силы: импульса это производная 4-вектора по отношению к
конечные компоненты вышеупомянутых 4-векторов Как и ожидалось, все являются стандартными 3-векторами, соответствующими пространственному 3-импульсу , 3-силе и т. д. [43] : 178–181 [37] : 36–59
4-векторы закон физический и
Первый постулат специальной теории относительности декларирует эквивалентность всех инерциальных систем отсчета. Физический закон, действующий в одном кадре, должен применяться во всех кадрах, поскольку в противном случае можно было бы различать кадры. Ньютоновские импульсы не ведут себя должным образом при лоренцевом преобразовании, и Эйнштейн предпочел изменить определение импульса на определение, включающее 4-вектора , вместо того, чтобы отказаться от сохранения импульса.
Физические законы должны основываться на конструкциях, независимых от системы координат. Это означает, что физические законы могут принимать форму уравнений, связывающих скаляры, которые всегда не зависят от системы отсчета. Однако уравнения, включающие 4-вектора, требуют использования тензоров соответствующего ранга, которые сами по себе можно рассматривать как построенные из 4-векторов . [43] : 186
Ускорение [ править ]
Распространено заблуждение, что специальная теория относительности применима только к инерциальным системам отсчета и что она не способна учитывать ускоряющиеся объекты или ускоряющиеся системы отсчета. На самом деле, ускоряющиеся объекты вообще можно анализировать, вообще не имея дело с ускоряющимися кадрами. Общая теория относительности требуется только тогда, когда гравитация существенна. [53]
Однако правильное обращение с ускоряющимися кадрами требует некоторой осторожности. Разница между специальной и общей теорией относительности состоит в том, что (1) В специальной теории относительности все скорости относительны, но ускорение абсолютно. (2) В общей теории относительности любое движение относительно, будь то инерционное, ускоряющееся или вращательное. Чтобы учесть эту разницу, общая теория относительности использует искривленное пространство-время. [53]
В этом разделе мы анализируем несколько сценариев, связанных с ускоренными системами отсчета.
космического корабля Совет-Беран Белл Парадокс -
Парадокс космического корабля Девана-Берана-Белла ( парадокс космического корабля Белла ) является хорошим примером проблемы, в которой интуитивное рассуждение без помощи геометрического понимания пространственно-временного подхода может привести к проблемам.

На рис. 4-4 два одинаковых космических корабля плывут в космосе и покоятся относительно друг друга. Они соединены веревкой, которая способна растягиваться лишь на ограниченное количество раз, прежде чем порвется. В данный момент в нашей системе координат, системе наблюдателя, оба космических корабля ускоряются в одном направлении вдоль линии между ними с одинаковым постоянным собственным ускорением. [примечание 13] Не порвется ли веревка?
Когда парадокс был новым и относительно неизвестным, даже профессиональным физикам было трудно найти решение. Две линии рассуждений приводят к противоположным выводам. Оба аргумента, представленные ниже, ошибочны, хотя один из них дает правильный ответ. [43] : 106, 120–122
- Для наблюдателей в кадре покоя космические корабли стартуют на расстоянии L друг от друга и остаются на том же расстоянии друг от друга во время ускорения. При ускорении L представляет собой сжатую длину расстояния L ' = γL в системе отсчета ускоряющихся космических кораблей. По прошествии достаточно длительного времени γ увеличится в достаточно большом разе, и струна должна порваться.
- Пусть A и B — задний и передний космические корабли. В кадре космических кораблей каждый космический корабль видит, как другой космический корабль делает то же самое, что и он. А говорит, что Б имеет такое же ускорение, как и он, и Б видит, что А повторяет каждое ее движение. Таким образом, космические корабли остаются на одинаковом расстоянии друг от друга, и нить не рвется. [43] : 106, 120–122
Проблема с первым аргументом заключается в том, что не существует «каркаса космических кораблей». Этого не может быть, потому что расстояние между двумя космическими кораблями увеличивается. Поскольку общего каркаса космических кораблей нет, длина струны не определена. Тем не менее, вывод верен, и аргументы в основном верны. Однако второй аргумент полностью игнорирует относительность одновременности. [43] : 106, 120–122
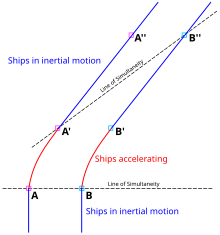
Диаграмма пространства-времени (рис. 4-5) почти сразу делает правильное решение этого парадокса очевидным. Два наблюдателя в пространстве-времени Минковского ускоряются с постоянной величиной. ускорение за нужное время (ускорение и прошедшее время измеряются самими наблюдателями, а не каким-то инерционным наблюдателем). Они сопутствующие и инерционные до и после этой фазы. В геометрии Минковского длина по линии одновременности оказывается больше длины по линии одновременности .
Увеличение длины можно рассчитать с помощью преобразования Лоренца. Если, как показано на рис. 4-5, ускорение закончено, в некотором кадре корабли останутся с постоянным смещением. Если и позиции кораблей в позиции в кадре являются: [54]
«Парадокс» как бы проистекает из того, как Белл построил свой пример. При обычном обсуждении лоренцева сокращения длина покоя фиксируется, а длина движения сокращается по мере измерения в кадре. . Как показано на рис. 4-5, пример Белла утверждает, что длины перемещения и измерено в кадре быть фиксированным, тем самым заставляя длину оставшегося кадра в рамке увеличить.
Ускоренный наблюдатель с горизонтом [ править ]
Определенные постановки задач специальной теории относительности могут привести к пониманию явлений, обычно связанных с общей теорией относительности, таких как горизонты событий . В тексте, сопровождающем рис. 2-7 , пурпурные гиперболы представляют реальные пути, которые отслеживает постоянно ускоряющийся путешественник в пространстве-времени. В периоды положительного ускорения скорость путешественника едва приближается к скорости света, в то время как, измеренное в нашей системе отсчёта, ускорение путешественника постоянно уменьшается.
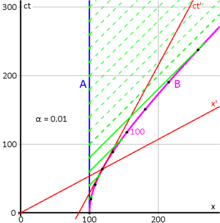
На рис. 4-6 более подробно показаны различные особенности движений путешественника. В любой момент ее пространственная ось формируется линией, проходящей через начало координат и ее текущее положение на гиперболе, а ее ось времени является касательной к гиперболе в ее положении. Параметр скорости приближается к пределу единицы, поскольку увеличивается. Так же, приближается к бесконечности.
Форма инвариантной гиперболы соответствует пути постоянного собственного ускорения. Это можно продемонстрировать следующим образом:
- Мы помним это
- С мы заключаем, что
- Из закона релятивистской силы
- Замена из шага 2 и выражение для из шага 3 дает что является постоянным выражением. [41] : 110–113
Рис. 4-6 иллюстрирует конкретный расчетный сценарий. Теренс (А) и Стелла (Б) изначально находятся вместе на расстоянии 100 световых часов от начала координат. Стелла взлетает в момент времени 0, ее космический корабль ускоряется со скоростью 0,01 градуса в час. Каждые двадцать часов Теренс сообщает Стелле по рации информацию о ситуации дома (сплошные зеленые линии). Стелла получает эти регулярные передачи, но увеличивающееся расстояние (частично компенсируемое замедлением времени) заставляет ее принимать сообщения Теренса все позже и позже, как указано на ее часах, и она никогда не получает никаких сообщений от Теренса после 100 часов на его часах (пунктирный зеленый линии). [41] : 110–113
Через 100 часов по часам Теренса Стелла попадает в темную область. Она путешествовала за пределы времениподобного будущего Теренса. С другой стороны, Теренс может продолжать получать сообщения от Стеллы бесконечно долго. Ему просто нужно ждать достаточно долго. Пространство-время разделено на отдельные области, разделенные видимым горизонтом событий. Пока Стелла продолжает ускоряться, она никогда не узнает, что происходит за горизонтом. [41] : 110–113
Введение в искривленное пространство-время [ править ]
Основные предложения [ править ]
Теории Ньютона предполагали, что движение происходит на фоне жесткой евклидовой системы отсчета, простирающейся через все пространство и все время. Гравитация осуществляется таинственной силой, действующей мгновенно на расстоянии, действия которой не зависят от промежуточного пространства. [примечание 14] Напротив, Эйнштейн отрицал существование какой-либо фоновой евклидовой системы отсчета, простирающейся во всем пространстве. Не существует и такой вещи, как сила гравитации, а есть только структура самого пространства-времени. [9] : 175–190
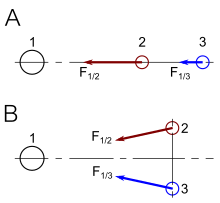
С точки зрения пространства-времени траектория спутника, вращающегося вокруг Земли, не определяется отдаленными влияниями Земли, Луны и Солнца. Вместо этого спутник движется в космосе только в ответ на местные условия. Поскольку пространство-время везде локально плоское, если рассматривать его в достаточно малом масштабе, спутник всегда движется по прямой линии в своей локальной инерциальной системе отсчета. Мы говорим, что спутник всегда следует по пути геодезической . Никакие доказательства гравитации не могут быть обнаружены при движении отдельной частицы. [9] : 175–190
При любом анализе пространства-времени доказательства существования гравитации требуют наблюдения относительных ускорений двух тел или двух разделенных частиц. На рис. 5-1 две отдельные частицы, свободно падающие в гравитационном поле Земли, демонстрируют приливное ускорение из-за локальных неоднородностей гравитационного поля, так что каждая частица следует различным путем в пространстве-времени. Приливные ускорения, которые эти частицы проявляют по отношению друг к другу, не требуют сил для своего объяснения. Скорее, Эйнштейн описал их в терминах геометрии пространства-времени, то есть кривизны пространства-времени. Эти приливные ускорения носят строго локальный характер. Это совокупный суммарный эффект многих локальных проявлений кривизны, которые приводят к появлению гравитационной силы, действующей на большом расстоянии от Земли. [9] : 175–190
В основе общей теории относительности лежат два центральных положения.
- Первой важной концепцией является независимость координат: законы физики не могут зависеть от того, какую систему координат мы используем. Это серьезное расширение принципа относительности из версии, используемой в специальной теории относительности, которая гласит, что законы физики должны быть одинаковыми для каждого наблюдателя, движущегося в неускоренных (инерциальных) системах отсчета. В общей теории относительности, если использовать собственные (переведенные) слова Эйнштейна, «законы физики должны иметь такую природу, чтобы их можно было применять к системам отсчета в любом виде движения». [55] : 113 Это приводит к немедленной проблеме: в ускоренных кадрах человек ощущает силы, которые, казалось бы, позволили бы ему оценить свое состояние ускорения в абсолютном смысле. Эйнштейн решил эту проблему с помощью принципа эквивалентности. [56] : 137–149

- Принцип эквивалентности гласит, что в любой достаточно маленькой области пространства эффекты гравитации такие же, как и эффекты ускорения.
- На рис. 5-2 человек А находится в космическом корабле, вдали от каких-либо массивных объектов, который испытывает равномерное ускорение g . Человек Б находится в ящике, лежащем на Земле. При условии, что космический корабль настолько мал, что приливные эффекты невозможно измерить (учитывая чувствительность современных приборов для измерения гравитации, А и Б, по-видимому, должны быть лилипутами ), не существует никаких экспериментов, которые А и Б могли бы провести, которые позволили бы им определить в какой настройке они находятся. [56] : 141–149
- Альтернативное выражение принципа эквивалентности заключается в том, что в универсальном законе гравитации Ньютона F = GMm g /r. 2 = m g g и во втором законе Ньютона F = m i a гравитационная нет априорной причины, по которой масса m g должна быть равна инерционной массе m i . Принцип эквивалентности утверждает, что эти две массы идентичны. [56] : 141–149
Чтобы перейти от приведенного выше элементарного описания искривленного пространства-времени к полному описанию гравитации, необходимы тензорное исчисление и дифференциальная геометрия — обе темы требуют значительного изучения. Без этих математических инструментов можно написать об общей теории относительности, но невозможно продемонстрировать какие-либо нетривиальные выводы.
Искривление времени [ править ]
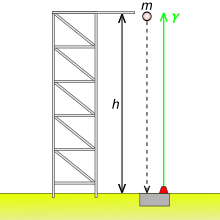
В обсуждении специальной теории относительности силы играли не более чем второстепенную роль. Специальная теория относительности предполагает способность определять инерциальные системы отсчета, заполняющие все пространство-время, все часы которых идут с той же скоростью, что и часы в начале координат. Действительно ли это возможно? Эксперимент показывает, что в неоднородном гравитационном поле ответ отрицательный. Гравитационные поля делают невозможным построение глобальной инерциальной системы отсчета. В достаточно малых областях пространства-времени локальные все еще возможны инерциальные системы отсчета. Общая теория относительности предполагает систематическое сшивание этих локальных рамок в более общую картину пространства-времени. [37] : 118–126
За годы до публикации общей теории в 1916 году Эйнштейн использовал принцип эквивалентности, чтобы предсказать существование гравитационного красного смещения в следующем мысленном эксперименте башня высотой h : (i) Предположим, что построена (рис. 5-3). (ii) Сбросьте частицу массы покоя m с вершины башни. Он свободно падает с ускорением g , достигая земли со скоростью v = (2 gh ). 1/2 , так что его полная энергия E , измеренная наблюдателем на земле, равна (iii) Преобразователь массы в энергию преобразует полную энергию частицы в один фотон высокой энергии, который направляется вверх. (iv) На вершине башни преобразователь энергии в массу преобразует энергию фотона E ' обратно в частицу с массой покоя m ' . [37] : 118–126
Должно быть так, что m = m ' , иначе можно было бы построить вечный двигатель . Поэтому мы предсказываем, что E ' = m , так что
Фотон, поднимающийся в гравитационном поле Земли, теряет энергию и смещается в красную сторону. Ранние попытки измерить это красное смещение с помощью астрономических наблюдений были несколько безрезультатными, но окончательные лабораторные наблюдения были выполнены Паундом и Ребкой (1959) , а затем Паундом и Снайдером (1964). [57]
Свет имеет связанную с ним частоту, и эту частоту можно использовать для управления работой часов. Гравитационное красное смещение приводит к важному выводу о самом времени: гравитация замедляет время. Предположим, мы построили два одинаковых часа, ход которых контролируется каким-то стабильным атомным переходом. Поместите одни часы на вершину башни, а другие останутся на земле. Экспериментатор на вершине башни замечает, что сигналы от наземных часов ниже по частоте, чем сигналы от часов рядом с ней на башне. Свет, идущий вверх по башне, — это всего лишь волна, и гребни волн не могут исчезнуть по пути вверх. На вершину башни приходит ровно столько же колебаний света, сколько излучалось внизу. Экспериментатор приходит к выводу, что наземные часы идут медленно, и может подтвердить это, опустив башенные часы для сравнения с наземными часами. [3] : 16–18 Для башни высотой 1 км расхождение составит около 9,4 наносекунд в день, что легко измерить с помощью современных приборов.
Часы в гравитационном поле не все идут с одинаковой скоростью. Такие эксперименты, как эксперимент Паунда-Ребки, твердо установили кривизну временного компонента пространства-времени. Эксперимент Паунда-Ребки ничего не говорит о кривизне пространственной составляющей пространства-времени. Но теоретические аргументы, предсказывающие гравитационное замедление времени, вообще не зависят от деталей общей теории относительности. Любая теория гравитации предсказывает гравитационное замедление времени, если она соблюдает принцип эквивалентности. [3] : 16 Сюда входит ньютоновская гравитация. Стандартная демонстрация в общей теории относительности состоит в том, чтобы показать, как в « ньютоновском пределе » (т. е. частицы движутся медленно, гравитационное поле слабое и поле статично) одной кривизны времени достаточно, чтобы вывести закон гравитации Ньютона. . [58] : 101–106
Ньютоновская гравитация — это теория искривленного времени. Общая теория относительности — это теория искривленного времени и искривленного пространства. Учитывая G как гравитационную постоянную, M как массу ньютоновской звезды и вращающиеся вокруг тела незначительной массы на расстоянии r от звезды, пространственно-временной интервал для ньютоновской гравитации является интервалом, для которого переменным является только временной коэффициент: [3] : 229–232
Искривление пространства [ править ]
The коэффициент перед описывает кривизну времени в ньютоновской гравитации, и эта кривизна полностью объясняет все ньютоновские гравитационные эффекты. Как и ожидалось, этот поправочный коэффициент прямо пропорционален и , и из-за в знаменателе поправочный коэффициент увеличивается по мере приближения к гравитирующему телу, а это означает, что время искривляется.
Но общая теория относительности — это теория искривленного пространства и искривленного времени, поэтому, если существуют условия, изменяющие пространственные компоненты пространственно-временного интервала, представленного выше, не следует ли их влияние наблюдать, скажем, на орбитах планет и спутников из-за применяемых поправочных коэффициентов кривизны? пространственным понятиям?
Ответ в том, что их можно увидеть, но эффект крошечный. Причина в том, что скорости планет чрезвычайно малы по сравнению со скоростью света, так что для планет и спутников Солнечной системы термин затмевает пространственные термины. [3] : 234–238
Несмотря на мелочность пространственных терминов, первые признаки того, что с ньютоновской гравитацией что-то не так, были обнаружены более полутора веков назад. В 1859 году Урбен Леверье , анализируя доступные наблюдения за транзитами Меркурия по диску Солнца с 1697 по 1848 год, сообщил, что известные физики не могут объяснить орбиту Меркурия, если только внутри него не существует планеты или пояса астероидов. орбита Меркурия. Перигелий орбиты Меркурия демонстрировал превышение скорости прецессии по сравнению с той, которую можно было объяснить притяжением других планет. [59] Способность обнаружить и точно измерить минутную величину этой аномальной прецессии (всего 43 угловых секунды за тропический век ) является свидетельством сложности астрометрии XIX века .

Как астроном, который ранее обнаружил существование Нептуна «на кончике пера», анализируя неравномерности орбиты Урана, заявление Леверье спровоцировало длившийся два десятилетия период «вулканомании», как среди профессиональных астрономов, так и среди астрономов-любителей. одинаково охотились за гипотетической новой планетой. Этот поиск включал несколько ложных наблюдений Вулкана. В конечном итоге было установлено, что такой планеты или пояса астероидов не существует. [60]
В 1916 году Эйнштейн должен был показать, что эта аномальная прецессия Меркурия объясняется пространственными условиями искривления пространства-времени. Искривление во временном плане, будучи просто выражением ньютоновской гравитации, не играет никакой роли в объяснении этой аномальной прецессии. Успех его вычислений стал для коллег Эйнштейна убедительным указанием на то, что общая теория относительности может быть верной.
Самым впечатляющим из предсказаний Эйнштейна был его расчет, согласно которому члены кривизны пространственных компонентов пространственно-временного интервала могут быть измерены при изгибании света вокруг массивного тела. Свет имеет наклон ±1 на диаграмме пространства-времени. Его движение в пространстве равно его движению во времени. Для слабополевого выражения инвариантного интервала Эйнштейн вычислил точно равную, но противоположный по знаку кривизну его пространственных компонент. [3] : 234–238
В гравитации Ньютона коэффициент перед предсказывает искривление света вокруг звезды. В общей теории относительности коэффициент перед предсказывает удвоение общего изгиба. [3] : 234–238
История экспедиции Эддингтона по затмению 1919 года и восхождения к славе Эйнштейна хорошо рассказана в другом месте. [61]
Источники искривления пространства-времени [ править ]

В теории гравитации Ньютона единственным источником гравитационной силы является масса .
Напротив, общая теория относительности помимо массы определяет несколько источников искривления пространства-времени. В уравнениях поля Эйнштейнаисточники гравитации представлены в правой части рисунка. тензор энергии-импульса . [62]
На рис. 5-5 классифицированы различные источники гравитации в тензоре энергии-импульса:
- (красный): общая плотность массы и энергии, включая любые вклады в потенциальную энергию от сил между частицами, а также кинетическую энергию от случайных тепловых движений.
- и (оранжевый): Это термины плотности импульса. Даже если объемного движения нет, энергия может передаваться за счет теплопроводности, а проводимая энергия будет нести импульс.
- – скорости потока i-й компоненты импульса на единицу площади в j -направлении . Даже если объемного движения нет, случайные тепловые движения частиц вызовут поток импульса, поэтому члены i = j (зеленые) представляют изотропное давление, а члены i ≠ j (синие) представляют напряжения сдвига. [62]
Один важный вывод, который можно сделать из уравнений, заключается в том, что, говоря в просторечии, гравитация сама по себе создает гравитацию . [примечание 15] Энергия имеет массу. Даже в ньютоновской гравитации гравитационное поле связано с энергией, называется гравитационной потенциальной энергией . В общей теории относительности энергия гравитационного поля возвращается в создание гравитационного поля. Это делает уравнения нелинейными, и их трудно решить ни в каких случаях, кроме случаев слабого поля. [3] : 240 Численная теория относительности — это раздел общей теории относительности, использующий численные методы для решения и анализа проблем, часто использующий суперкомпьютеры для изучения черных дыр , гравитационных волн , нейтронных звезд и других явлений в режиме сильного поля.
Энергия-импульс [ править ]
В специальной теории относительности масса-энергия тесно связана с импульсом . Точно так же, как пространство и время — это разные аспекты более всеобъемлющей сущности, называемой пространством-временем, масса-энергия и импульс — это просто разные аспекты единой четырехмерной величины, называемой четырьмя импульсами . Следовательно, если масса-энергия является источником гравитации, то импульс также должен быть источником. Включение импульса в качестве источника гравитации приводит к предсказанию, что движущиеся или вращающиеся массы могут генерировать поля, аналогичные магнитным полям, создаваемым движущимися зарядами, — явление, известное как гравитомагнетизм . [63]

Хорошо известно, что силу магнетизма можно определить, применив правила специальной теории относительности к движущимся зарядам. (Красноречивая демонстрация этого была представлена Фейнманом в томе II, главах 13–6 , его «Лекций по физике» , доступных в Интернете.) [64] Аналогичную логику можно использовать, чтобы продемонстрировать происхождение гравитомагнетизма. [3] : 245–253
На рис. 5-7а два параллельных бесконечно длинных потока массивных частиц имеют равные и противоположные скорости - v и + v относительно покоящейся пробной частицы, центрированной между ними. Из-за симметрии установки результирующая сила, действующая на центральную частицу, равна нулю. Предполагать так что скорости просто складываются. На рис. 5-7б показана точно такая же установка, но в кадре верхнего потока. Пробная частица имеет скорость + v , а донный поток имеет скорость + 2v . Поскольку физическая ситуация не изменилась, а только рамка, в которой наблюдаются вещи, пробная частица не должна притягиваться ни к одному из потоков. [3] : 245–253
Совсем не ясно, равны ли силы, действующие на пробную частицу. (1) Поскольку нижний поток движется быстрее верхнего, каждая частица нижнего потока имеет большую массовую энергию, чем частица верхнего потока. (2) Из-за лоренцева сжатия в нижнем потоке на единицу длины приходится больше частиц, чем в верхнем. (3) Другой вклад в активную гравитационную массу придонного потока вносит дополнительный член давления, для обсуждения которого на данный момент у нас нет достаточных оснований. Все эти эффекты вместе, по-видимому, потребуют, чтобы пробная частица была притянута к нижнему потоку. [3] : 245–253
Пробная частица не притягивается к нижнему потоку из-за зависящей от скорости силы, которая отталкивает частицу , движущуюся в том же направлении, что и нижний поток. Этот гравитационный эффект, зависящий от скорости, называется гравитомагнетизмом. [3] : 245–253
Следовательно, материя, движущаяся через гравитомагнитное поле, подвержена так называемым эффектам перетаскивания системы координат, аналогичным электромагнитной индукции . Было высказано предположение, что такие гравитомагнитные силы лежат в основе генерации релятивистских струй (рис. 5-8), выбрасываемых некоторыми вращающимися сверхмассивными черными дырами . [65] [66]
Давление и стресс [ править ]
Источниками гравитации также должны быть величины, которые напрямую связаны с энергией и импульсом, а именно внутреннее давление и напряжение . Взятые вместе, масса-энергия , импульс, давление и напряжение служат источниками гравитации: в совокупности они определяют пространство-время, как искривляться.
Общая теория относительности предсказывает, что давление действует как источник гравитации с точно такой же силой, что и плотность массы-энергии. Включение давления в качестве источника гравитации приводит к резким различиям между предсказаниями общей теории относительности и предсказаниями ньютоновской гравитации. Например, термин давления устанавливает максимальный предел массы нейтронной звезды . Чем массивнее нейтронная звезда, тем большее давление требуется, чтобы выдержать ее вес против силы тяжести. Однако повышенное давление усиливает гравитацию, действующую на массу звезды. Выше определенной массы, определяемой пределом Толмана-Оппенгеймера-Волкова , процесс становится неконтролируемым, и нейтронная звезда коллапсирует в черную дыру . [3] : 243, 280
Условия напряжения становятся очень важными при выполнении таких расчетов, как гидродинамическое моделирование сверхновых с коллапсом ядра. [67]
Эти предсказания о роли давления, импульса и напряжения как источников искривления пространства-времени изящны и играют важную роль в теории. Что касается давления, то в ранней Вселенной доминировало излучение. [68] и весьма маловероятно, что какие-либо соответствующие космологические данные (например, обилие нуклеосинтеза и т. д.) могли быть воспроизведены, если бы давление не вносило вклад в гравитацию или если бы оно не имело той же силы в качестве источника гравитации, что и масса-энергия. Точно так же математическая последовательность уравнений поля Эйнштейна была бы нарушена, если бы члены напряжения не выступали в качестве источника гравитации.
Экспериментальная проверка источников искривления пространства-времени [ править ]
: Активная, пассивная и инерционная масса . Определения
Бонди различает различные возможные типы массы: (1) активная масса ( ) — масса, выступающая источником гравитационного поля; (2) пассивная масса ( ) — масса, реагирующая на гравитационное поле; (3) инерционная масса ( ) — это масса, реагирующая на ускорение. [69]
- то же самое, что гравитационная масса ( ) при обсуждении принципа эквивалентности .
В теории Ньютона,
- Третий закон действия и противодействия гласит, что и должно быть то же самое.
- С другой стороны, ли и равны, является эмпирическим результатом.
В общей теории относительности
- Равенство и диктуется принципом эквивалентности.
- Не существует принципа «действия и противодействия», диктующего какие-либо необходимые отношения между и . [69]
Давление как источник гравитации [ править ]
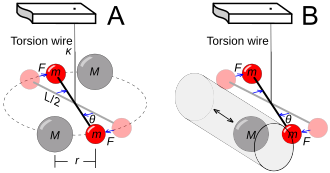
Классический эксперимент по измерению силы гравитационного источника (т.е. его активной массы) впервые был проведен в 1797 году Генри Кавендишем (рис. 5-9а). Два маленьких, но плотных шарика подвешены на тонкой проволоке, образуя крутильные весы . Поднесение двух больших испытательных масс к шарикам создает заметный крутящий момент. Зная размеры аппарата и измеримую жесткость пружины крученой проволоки, гравитационную постоянную G. можно определить
Изучать эффекты давления путем сжатия пробных масс безнадежно, так как достижимые лабораторные давления ничтожны по сравнению с массой-энергией металлического шара.
Однако отталкивающее электромагнитное давление, возникающее из-за того, что протоны плотно сжимаются внутри атомных ядер, обычно составляет порядка 10 28 атм ≈ 10 33 Ну ≈ 10 33 кг·с −2 м −1 . Это составляет около 1% от плотности ядерной массы примерно 10 18 кг/м 3 (после факторинга c 2 ≈ 9×10 16 м 2 с −2 ). [70]
Если давление не выступает источником гравитации, то соотношение должно быть ниже для ядер с более высоким атомным номером Z , у которых электростатическое давление выше. Л.Б.Кройцер (1968) провел эксперимент Кавендиша, используя тефлоновую массу, суспендированную в смеси жидкостей трихлорэтилена и дибромэтана, имеющих ту же плавучую плотность, что и тефлон (рис. 5-9б). У фтора атомный номер Z = 9 , а у брома Z = 35 . Кройцер обнаружил, что изменение положения тефлоновой массы не вызывает дифференциального отклонения торсиона, следовательно, активная масса и пассивная масса эквивалентны точности 5 × 10. −5 . [71]
Хотя Кройцер первоначально рассматривал этот эксперимент просто как проверку отношения активной массы к пассивной массе, Клиффорд Уилл (1976) переосмыслил эксперимент как фундаментальную проверку связи источников с гравитационными полями. [72]
В 1986 году Бартлетт и Ван Бюрен отметили, что лазерная локация Луны обнаружила смещение на 2 км между центром фигуры Луны и ее центром масс. Это указывает на асимметрию в распределении Fe (в изобилии содержится в ядре Луны) и Al (в изобилии в ее коре и мантии). Если бы давление не вносило такого же вклада в искривление пространства-времени, как масса-энергия, Луна не находилась бы на орбите, предсказанной классической механикой. Они использовали свои измерения, чтобы ужесточить пределы любых расхождений между активной и пассивной массой примерно до 10. −12 . [73] Имея десятилетия дополнительных данных о лунной лазерной локации, Сингх и др. (2023) сообщили об улучшении этих пределов примерно в 100 раз. [74]
Гравитомагнетизм [ править ]
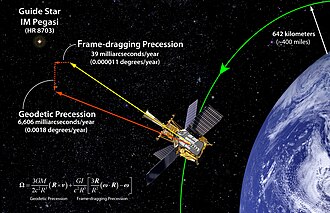
Существование гравитомагнетизма было доказано гравитационным зондом B (GP-B) , спутниковой миссией, запущенной 20 апреля 2004 года. [75] Этап космического полета продолжался до . Целью миссии было измерение кривизны пространства-времени вблизи Земли, уделяя особое внимание гравитомагнетизму .
Первоначальные результаты подтвердили относительно большой геодезический эффект (который обусловлен простой кривизной пространства-времени и также известен как прецессия де Ситтера) с точностью около 1%. Гораздо меньший эффект перетаскивания системы координат (который возникает из-за гравимагнетизма и также известен как прецессия Лензе – Тирринга ) было трудно измерить из-за неожиданных эффектов заряда, вызывающих переменный дрейф в гироскопах. Тем не менее, по эффект перетаскивания кадров был подтвержден с точностью до 15% от ожидаемого результата, [76] в то время как геодезический эффект был подтвержден на уровне более 0,5%. [77] [78]
Последующие измерения перетаскивания кадра с помощью наблюдений с лазерной дальностью спутников LARES , LAGEOS -1 и LAGEOS-2 улучшили результаты измерения GP-B , при этом результаты (по состоянию на 2016 год) демонстрируют эффект с точностью до 5% от его теоретического значения. [79] хотя были некоторые разногласия по поводу точности этого результата. [80]
Другая попытка, эксперимент «Гироскопы в общей теории относительности» (GINGER), направлена на использование трех кольцевых лазеров длиной 6 м , установленных под прямым углом друг к другу на высоте 1400 м ниже поверхности Земли, для измерения этого эффекта. [81] [82]
Технические темы [ править ]
Действительно ли пространство-время искривлено? [ редактировать ]
взглядам Пуанкаре Согласно конвенционалистским , основными критериями, согласно которым следует выбирать евклидову или неевклидову геометрию, являются экономичность и простота. Реалист сказал бы, что Эйнштейн обнаружил, что пространство-время неевклидово. Конвенционалист сказал бы, что Эйнштейну просто было удобнее использовать неевклидову геометрию. Конвенционалист утверждает, что анализ Эйнштейна ничего не говорит о том, что на самом деле представляет собой геометрия пространства-времени. [83]
Такое, как говорится,
- 1. Можно ли представить общую теорию относительности в терминах плоского пространства-времени?
- 2. Существуют ли ситуации, когда интерпретация общей теории относительности в плоском пространстве-времени может быть более удобной , чем обычная интерпретация искривленного пространства-времени?
В ответ на первый вопрос ряд авторов, в том числе Дезер, Грищук, Розен, Вайнберг и др., дали различные формулировки гравитации как поля в плоском многообразии. Эти теории по-разному называют « биметрической гравитацией », «теоретико-полевым подходом к общей теории относительности» и так далее. [84] [85] [86] [87] Кип Торн представил популярный обзор этих теорий. [88] : 397–403
Парадигма плоского пространства-времени утверждает, что материя создает гравитационное поле, которое заставляет линейки сжиматься, когда они поворачиваются от окружной ориентации к радиальной, и это приводит к замедлению скорости тикания часов. Парадигма плоского пространства-времени полностью эквивалентна парадигме искривленного пространства-времени, поскольку они оба представляют одни и те же физические явления. Однако их математические формулировки совершенно различны. Действующие физики обычно переключаются между использованием методов искривленного и плоского пространства-времени в зависимости от требований задачи. Парадигма плоского пространства-времени удобна при проведении приближенных расчетов в слабых полях. Следовательно, методы плоского пространства-времени, как правило, используются при решении задач гравитационных волн, а методы искривленного пространства-времени, как правило, используются при анализе черных дыр. [88] : 397–403
симметрии Асимптотические
Группа симметрии пространства-времени для специальной теории относительности — это группа Пуанкаре , которая представляет собой десятимерную группу из трех усилений Лоренца, трех вращений и четырех сдвигов пространства-времени. Логично задаться вопросом, какие симметрии, если таковые имеются, могут применяться в общей теории относительности . Разрешимым случаем может быть рассмотрение симметрии пространства-времени, как ее видят наблюдатели, находящиеся вдали от всех источников гравитационного поля. Наивное ожидание асимптотически плоского пространства-времени может заключаться в простом расширении и воспроизведении симметрии плоского пространства-времени специальной теории относительности, а именно. , группа Пуанкаре.
В 1962 году Герман Бонди , М.Г. ван дер Бург, А.В. Мецнер. [89] и Райнер К. Сакс [90] обратился к этой проблеме асимптотической симметрии , чтобы исследовать поток энергии на бесконечности, вызванный распространяющимися гравитационными волнами . Их первым шагом было принятие решения о некоторых физически разумных граничных условиях, которые следует разместить в гравитационном поле на светоподобной бесконечности, чтобы охарактеризовать то, что значит сказать, что метрика асимптотически плоская, не делая никаких априорных предположений о природе асимптотической группы симметрии - даже предположение о существовании такой группы. Затем, после разработки того, что они считали наиболее разумными граничными условиями, они исследовали природу полученных в результате преобразований асимптотической симметрии, которые оставляют инвариантной форму граничных условий, подходящую для асимптотически плоских гравитационных полей. [91] : 35
Они обнаружили, что преобразования асимптотической симметрии действительно образуют группу, и структура этой группы не зависит от конкретного гравитационного поля, которое случайно присутствует. Это означает, что, как и ожидалось, можно отделить кинематику пространства-времени от динамики гравитационного поля по крайней мере на пространственной бесконечности. Загадочным сюрпризом в 1962 году стало открытие богатой бесконечномерной группы (так называемой группы БМС) в качестве асимптотической группы симметрии вместо конечномерной группы Пуанкаре, которая является подгруппой группы БМС. Преобразования Лоренца не только являются преобразованиями асимптотической симметрии, но существуют также дополнительные преобразования, которые не являются преобразованиями Лоренца, но являются преобразованиями асимптотической симметрии. Фактически, они обнаружили дополнительную бесконечность генераторов преобразований, известных как супертрансляции . Отсюда следует вывод, что общая теория относительности (ОТО) не сводится к специальной теории относительности в случае слабых полей на больших расстояниях. [91] : 35
Риманова геометрия [ править ]
Риманова геометрия — это раздел дифференциальной геометрии , изучающий римановы многообразия , определяемые как гладкие многообразия с римановой метрикой ( скалярным произведением в касательном пространстве в каждой точке, которое плавно меняется от точки к точке). Это дает, в частности, локальные понятия угла , длины кривых , площади поверхности и объема . Из них можно получить некоторые другие глобальные величины путем интегрирования местных вкладов.
Риманова геометрия возникла из видения Бернхарда Римана, выраженного в его вступительной лекции « Ueber die Hypothesen, welche der Geometrie zu Grundeliegen » («О гипотезах, на которых основана геометрия»). [92] Это очень широкое и абстрактное обобщение дифференциальной геометрии поверхностей в R. 3 . Развитие римановой геометрии привело к синтезу разнообразных результатов, касающихся геометрии поверхностей и поведения геодезических на них, с методами, которые можно применить к изучению дифференцируемых многообразий более высоких размерностей. Это позволило сформулировать Эйнштейна общую теорию относительности , оказало глубокое влияние на теорию групп и теорию представлений , а также анализ и стимулировало развитие алгебраической и дифференциальной топологии .Изогнутые коллекторы [ править ]
По физическим причинам пространственно-временной континуум математически определяется как четырехмерное гладкое связное лоренцево многообразие. . Это означает гладкую метрику Лоренца есть подпись . Метрика определяет геометрия пространства-времени , а также определение геодезических частиц и световых лучей. Для каждой точки (события) на этом многообразии карты координат используются для представления наблюдателей в системах отсчета. Обычно декартовы координаты используются. Причем для простоты единицы измерения обычно выбираются такие, что скорость света равен 1. [93]
Система отсчета (наблюдатель) может быть идентифицирована с помощью одной из этих координатных карт; любой такой наблюдатель может описать любое событие . Другая система отсчета может быть идентифицирована по второй карте координат около . Два наблюдателя (по одному в каждой системе отсчета) могут описать одно и то же событие. но получить разные описания. [93]
Обычно для покрытия многообразия требуется множество перекрывающихся координатных карт. Даны две координатные карты, одна из которых содержит (представляющий наблюдателя) и другой, содержащий (представляя другого наблюдателя), пересечение диаграмм представляет собой область пространства-времени, в которой оба наблюдателя могут измерять физические величины и, следовательно, сравнивать результаты. Связь между двумя наборами измерений задается неособым преобразованием координат на этом пересечении. Идея координатных карт как локальных наблюдателей, которые могут выполнять измерения поблизости, также имеет хороший физический смысл, поскольку именно так на самом деле собираются физические данные — локально. [93]
Например, два наблюдателя, один из которых находится на Земле, а другой находится на быстрой ракете к Юпитеру, могут наблюдать врезающуюся в Юпитер комету (это событие ). В общем, они не согласятся относительно точного места и времени этого воздействия, т. е. у них будут разные четверки. (поскольку они используют разные системы координат). Хотя их кинематические описания будут различаться, динамические (физические) законы, такие как сохранение импульса и первый закон термодинамики, все равно будут соблюдаться. На самом деле теория относительности требует большего, в том смысле, что она требует, чтобы эти (и все другие физические) законы принимали одинаковую форму во всех системах координат. Это вводит в теорию относительности тензоры , которыми представлены все физические величины.
Геодезические называются времяподобными, нулевыми или пространственноподобными, если касательный вектор к одной точке геодезической имеет такую природу. Пути частиц и световых лучей в пространстве-времени представляются времениподобными и нулевыми (светоподобными) геодезическими соответственно. [93]
3+1 пространства - времени Привилегированный персонаж
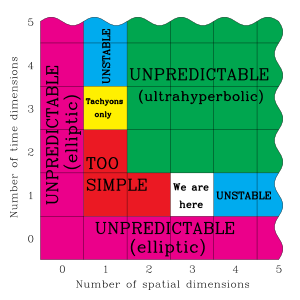
Существует два вида измерений: пространственные (двунаправленные) и временные (однонаправленные). [95] Пусть количество пространственных измерений равно N , а количество временных измерений равно T . Тот факт, что N = 3 и T = 1 , если оставить в стороне компактифицированные измерения, вызываемые теорией струн и не обнаруживаемые до сих пор, можно объяснить, апеллируя к физическим последствиям, когда N отличается от 3, а T отличается от 1. Аргумент часто носит неуместный характер. антропный характер и, возможно, первый в своем роде, хотя и до того, как полная концепция вошла в моду.
Неявное представление о том, что размерность Вселенной особенная, впервые приписывается Готфриду Вильгельму Лейбницу , который в « Рассуждениях о метафизике» предположил, что мир есть « тот, который одновременно является самым простым в гипотезах и самым богатым в явлениях ». [96] Иммануил Кант утверждал, что трехмерное пространство является следствием закона обратных квадратов всемирного тяготения . Хотя аргумент Канта имеет историческое значение, Джон Д. Барроу сказал, что он «переносит суть с самого начала: именно трехмерность пространства объясняет, почему мы видим в Природе законы силы обратных квадратов, а не наоборот». (Барроу 2002:204). [примечание 16]
В 1920 году Пауль Эренфест что если существует только одно временное измерение и более трех пространственных измерений, орбита планеты показал , вокруг Солнца не может оставаться стабильной. То же самое относится и к орбите звезды вокруг центра ее галактики . [97] Эренфест также показал, что если пространственных измерений четное количество, то разные части волнового импульса будут двигаться с разной скоростью. Если есть пространственных измерениях, где k — целое положительное число, то волновые импульсы искажаются. В 1922 году Герман Вейль заявил, что быть теория электромагнетизма Максвелла может выражена через действие только для четырехмерного многообразия. [98] Наконец, Тангерлини показал в 1963 году, что когда существует более трех пространственных измерений, электронные орбитали вокруг ядер не могут быть стабильными; электроны либо упадут в ядро , либо рассеются. [99]
Макс Тегмарк развивает предыдущий аргумент в следующей антропной манере. [100] Если T отличается от 1, поведение физических систем не может быть надежно предсказано на основе знания соответствующих уравнений в частных производных . В такой вселенной не могла бы возникнуть разумная жизнь, способная манипулировать технологиями. Более того, если T > 1 , Тегмарк утверждает, что протоны и электроны были бы нестабильными и могли бы распадаться на частицы, имеющие большую массу, чем они сами. (Это не проблема, если частицы имеют достаточно низкую температуру.) [100] Наконец, если N < 3 , гравитация любого вида становится проблематичной, и Вселенная, вероятно, будет слишком простой, чтобы вместить наблюдателей. Например, когда N < 3 , нервы не могут пересекаться, не пересекаясь. [100] Следовательно, антропные и другие аргументы исключают все случаи, кроме N = 3 и T = 1 , которые описывают мир вокруг нас.
С другой стороны, учитывая создание черных дыр из идеального одноатомного газа под действием его самогравитации, Вэй-Сян Фэн показал, что (3 + 1) -мерное пространство-время является предельной размерностью. Более того, именно уникальная размерность может позволить себе «стабильную» газовую сферу с «положительной» космологической постоянной . Однако самогравитирующий газ не может быть устойчиво связан, если массовая сфера превышает ~10 21 солнечных масс из-за небольшой положительности наблюдаемой космологической постоянной. [101]
В 2019 году Джеймс Скаргилл утверждал, что сложная жизнь возможна в двух пространственных измерениях. По мнению Скаргилла, чисто скалярная теория гравитации может учитывать локальную гравитационную силу, а двумерных сетей может быть достаточно для сложных нейронных сетей. [102] [103]См. также [ править ]
- Базовое введение в математику искривленного пространства-времени
- Комплексное пространство-время
- Мысленные эксперименты Эйнштейна
- Четырехмерность
- География
- Глобальная структура пространства-времени
- Список пространств-временей
- Метрическое пространство
- Философия пространства и времени
- Подарок
- География времени
Примечания [ править ]
- ^ светоносный от латинского lumen — свет, + ferens — несущий; эфир от греческого αἰθήρ ( aithēr ), чистый воздух, ясное небо.
- ^ Заявляя, что одновременность является вопросом соглашения, Пуанкаре имел в виду, что, чтобы вообще говорить о времени, необходимо иметь синхронизированные часы, а синхронизация часов должна быть установлена с помощью определенной оперативной процедуры (конвенции). Эта позиция представляла собой фундаментальный философский отход от Ньютона, который представлял абсолютное, истинное время, независимое от работы неточных часов его времени. Эта позиция также представляла собой прямую атаку на влиятельного философа Анри Бергсона , который утверждал, что время, одновременность и продолжительность являются вопросами интуитивного понимания. [19]
- ^ Операционная процедура, принятая Пуанкаре, по существу идентична так называемой синхронизации Эйнштейна , хотя ее вариант уже широко использовался телеграфистами в середине 19 века. По сути, для синхронизации двух часов одни подают световой сигнал от одних к другим и настраивают время, необходимое для срабатывания вспышки. [19]
- ↑ Отличительной чертой карьеры Эйнштейна, по сути, было использование им визуализированных мысленных экспериментов (Gedanken-Experimente) в качестве фундаментального инструмента для понимания физических проблем. В специальной теории относительности он использовал движущиеся поезда и вспышки молний для своих самых глубоких идей. В качестве искривленного пространства-времени он рассматривал падение художника с крыши, ускоряющиеся лифты, слепых жуков, ползающих по искривленным поверхностям и тому подобное. В своих великих Сольвеевских дебатах с Бором о природе реальности (1927 и 1930) он разработал множество воображаемых приспособлений, призванных показать, по крайней мере в теории, средства, с помощью которых принцип неопределенности Гейзенберга можно обойти . Наконец, внося глубокий вклад в литературу по квантовой механике, Эйнштейн рассмотрел две частицы, кратковременно взаимодействующие, а затем разлетающиеся так, что их состояния коррелируют, предвосхищая явление, известное как квантовая запутанность . [24]
- ↑ В оригинальной версии этой лекции Минковский продолжал использовать такие устаревшие термины, как эфир, но посмертная публикация в 1915 году этой лекции в « Анналах физики» ( Annalen der Physik ) была отредактирована Зоммерфельдом, чтобы удалить этот термин. Зоммерфельд также отредактировал опубликованную форму этой лекции, чтобы пересмотреть суждение Минковского об Эйнштейне и превратить его из простого разъяснения принципа относительности в его главного толкователя. [25]
- ^ (В дальнейшем группа G ∞ является группой Галилея, а группа G c группой Лоренца.) «Относительно этого ясно, что группа G c в пределе для c = ∞ , т.е. как группа G ∞ , в точности становится полной группой, принадлежащей ньютоновской механике. При таком положении дел, и поскольку G c математически более понятна, чем G ∞ , математик может посредством свободной игры воображения прийти к мысли, что явления природы действительно обладают инвариантность не для группы G ∞ , а скорее для группы G c , где c определенно конечно и только чрезвычайно велико при использовании обычных единиц измерения». [27]
- ^ Например, группа Лоренца является подгруппой конформной группы в четырех измерениях . [28] : 41–42 Группа Лоренца изоморфна группе Лагерра, преобразующей плоскости в плоскости, [28] : 39–42 он изоморфен группе Мёбиуса плоскости, [29] : 22 и изоморфен группе изометрий в гиперболическом пространстве , которая часто выражается в терминах модели гиперболоида . [30] : 3.2.3
- ^ В декартовой плоскости обычное вращение оставляет круг неизменным. В пространстве-времени гиперболическое вращение сохраняет гиперболическую метрику .
- ^ Даже без (замедления) ускорения, т. е. с использованием одной инерциальной системы отсчета O для постоянного высокоскоростного движения наружу и другой инерциальной системы I для постоянного высокоскоростного движения внутрь - сумма прошедшего времени в этих кадрах (O и I) короче, чем прошедшее время в стационарной инерциальной системе отсчета S. Таким образом, ускорение и замедление не являются причиной более короткого прошедшего времени во время движения наружу и внутрь. Вместо этого использование двух разных постоянных и высокоскоростных инерциальных систем для движения наружу и внутрь на самом деле является причиной более короткого общего прошедшего времени. Конечно, если одному и тому же близнецу необходимо пройти внешний и внутренний участок пути и безопасно переключиться с внешнего на внутренний участок пути, потребуется ускорение и замедление. Если бы путешествующий близнец мог двигаться по высокоскоростной внешней инерциальной системе отсчета и мгновенно переключиться на высокоскоростную внутреннюю инерциальную систему отсчета, этот пример все равно работал бы. Дело в том, что истинная причина должна быть четко указана. Асимметрия возникает из-за сравнения суммы прошедшего времени в двух разных инерциальных системах отсчета (O и I) с прошедшим временем в одной инерциальной системе отсчета S.
- ^ Простота анализа релятивистского сценария часто зависит от рамки, в которой вы решаете выполнить анализ. На этом связанном изображении мы представляем альтернативные взгляды на сценарий поперечного доплеровского сдвига, где источник и приемник находятся максимально близко друг к другу.(а) Если мы проанализируем сценарий в рамках получателя, мы обнаружим, что анализ более сложен, чем должен быть. Видимое положение небесного объекта смещается от его истинного положения (или геометрического положения) из-за движения объекта в течение того времени, когда его свет достигает наблюдателя. Источник будет замедлен во времени относительно приемника, но красное смещение, подразумеваемое этим замедлением времени, будет компенсироваться синим смещением из-за продольной составляющей относительного движения между приемником и видимым положением источника.(б) Гораздо проще, если вместо этого мы проанализируем сценарий с точки зрения источника. Наблюдатель, находящийся у источника, из постановки задачи знает, что приемник находится в ближайшей к нему точке. Это означает, что приемник не имеет продольной составляющей движения, что усложняет анализ. Поскольку часы приемника замедлены по времени относительно источника, свет, который получает приемник, смещается в синюю сторону в несколько раз. гамма .
- ^ Не все эксперименты характеризуют эффект с точки зрения красного смещения. Например, в эксперименте Кюндига измеряется поперечное голубое смещение с использованием мессбауэровской установки источника в центре ротора центрифуги и поглотителя на ободе.
- ^ Быстрота возникает естественным образом как координаты чистых буст-генераторов внутри алгебры алгебры Ли группы Лоренца. Точно так же углы поворота естественным образом возникают как координаты (по модулю 2 π ) на генераторах чистого вращения в алгебре Ли. (Вместе они координируют всю алгебру Ли.) Заметное отличие состоит в том, что результирующие вращения являются периодическими по углу поворота, в то время как результирующие повышения не являются периодическими по быстроте (а скорее взаимно однозначными). Сходство между повышениями и ротациями является формальным сходством.
- ^ В теории относительности собственное ускорение — это физическое ускорение (т. е. измеримое ускорение, измеряемое акселерометром), испытываемое объектом. Таким образом, это ускорение относительно свободно падающего или инерционного наблюдателя, который на мгновение находится в покое относительно измеряемого объекта.
- ^ Сам Ньютон остро осознавал трудности, присущие этим предположениям, но на практике принятие этих предположений было единственным способом добиться прогресса. В 1692 году он писал своему другу Ричарду Бентли: «Гравитация должна быть врожденной, присущей и существенной для Материи, так что одно тело может воздействовать на другое на расстоянии через Вакуум, без посредничества чего-либо другого, посредством и посредством которого их действие и сила могут передаваться от одного к другому, является для меня настолько великим абсурдом, что я верю, что ни один человек, обладающий в философских вопросах компетентной способностью мышления, никогда не сможет впасть в это».
- ^ Точнее, гравитационное поле соединяется само с собой. В ньютоновской гравитации потенциал двух точечных масс представляет собой просто сумму потенциалов двух масс, но это не применимо к ОТО. Это можно рассматривать как результат принципа эквивалентности: если бы гравитация не связывалась сама с собой, две частицы, связанные взаимным гравитационным притяжением, не имели бы ту же инерционную массу (из-за отрицательной энергии связи), что и их гравитационная масса. [58] : 112–113
- ^ Это потому, что закон гравитации (или любой другой закон обратных квадратов ) вытекает из концепции потока и пропорциональной зависимости плотности потока и напряженности поля. Если N = 3 , то трехмерные твердые объекты имеют площади поверхности, пропорциональные квадрату их размера в любом выбранном пространственном измерении. В частности, сфера радиуса r имеет площадь поверхности 4 πr. 2 . В более общем смысле, в пространстве N измерений сила гравитационного притяжения между двумя телами, разделенными расстоянием r, будет обратно пропорциональна r. Н -1 .
Дополнительная информация [ править ]
- ^ Разные репортеры, просматривающие сценарии, представленные на этом рисунке, интерпретируют сценарии по-разному в зависимости от своего знания ситуации. (i) Первый репортер, находясь в центре масс частиц 2 и 3, но не зная о большой массе 1 , приходит к выводу, что между частицами в сценарии A между частицами существует сила притяжения. существует сила отталкивания, в то время как в сценарии B . (ii) Второй репортер, зная о большой массе 1 , улыбается наивности первого репортера. Этот второй репортер знает, что на самом деле кажущиеся силы между частицами 2 и 3 на самом деле представляют собой приливные эффекты, возникающие в результате их дифференциального притяжения по массе 1 . (iii) Третий репортер, обученный общей теории относительности, знает, что на самом деле между тремя объектами вообще не существует никаких сил. Скорее, все три объекта движутся по геодезическим линиям в пространстве-времени.
Ссылки [ править ]
- ^ Ринасевич, Роберт (12 августа 2004 г.). «Взгляды Ньютона на пространство, время и движение» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. Архивировано из оригинала 16 июля 2012 года . Проверено 24 марта 2017 г.
- ^ Дэвис, Филип Дж. (2006). Математика и здравый смысл: случай творческого напряжения . Уэлсли, Массачусетс: АК Питерс. п. 86. ИСБН 978-1-4398-6432-6 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С Шютц, Бернард (2004). Гравитация с нуля: Вводное руководство по гравитации и общей теории относительности (переиздание). Кембридж: Издательство Кембриджского университета . ISBN 0-521-45506-5 . Архивировано из оригинала 17 января 2023 года . Проверено 24 мая 2017 г.
- ^ Фок, В. (1966). Теория пространства, времени и гравитации (2-е изд.). Нью-Йорк: Pergamon Press Ltd., с. 33. ISBN 0-08-010061-9 . Проверено 14 октября 2023 г.
- ^ Лоуден, Д.Ф. (1982). Введение в тензорное исчисление, теорию относительности и космологию (3-е изд.). Минеола, Нью-Йорк: Dover Publications. п. 7. ISBN 978-0-486-42540-5 .
- ^ Jump up to: Перейти обратно: а б с д и Кольер, Питер (2017). Самая непостижимая вещь: заметки к очень мягкому введению в математику относительности (3-е изд.). Непонятные книги. ISBN 978-0-9573894-6-5 .
- ^ Роуленд, Тодд. «Многообразие» . Вольфрам Математический мир . Вольфрам Исследования. Архивировано из оригинала 13 марта 2017 года . Проверено 24 марта 2017 г.
- ^ Jump up to: Перейти обратно: а б Французский, AP (1968). Специальная теория относительности . Бока-Ратон, Флорида : CRC Press . стр. 35–60. ISBN 0-7487-6422-4 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я Тейлор, Эдвин Ф.; Уиллер, Джон Арчибальд (1992). Физика пространства-времени: Введение в специальную теорию относительности (2-е изд.). Сан-Франциско, Калифорния: Фриман. ISBN 0-7167-0336-Х . Проверено 14 апреля 2017 г.
- ^ Шерр, Рэйчел Э .; Шаффер, Питер С.; Вокос, Стаматис (июль 2001 г.). «Студенческое понимание времени в специальной теории относительности: одновременность и системы отсчета» (PDF) . Американский журнал физики . 69 (С1). Колледж-Парк, Мэриленд: Американская ассоциация учителей физики : S24–S35. arXiv : физика/0207109 . Бибкод : 2001AmJPh..69S..24S . дои : 10.1119/1.1371254 . S2CID 8146369 . Архивировано (PDF) из оригинала 28 сентября 2018 года . Проверено 11 апреля 2017 г.
- ^ Хьюз, Стефан (2013). Ловцы света: Улавливая космос: Происхождение, Луна, Солнечная система, Солнечная система и глубокий космос . Пафос, Кипр: Издательство ArtDeCiel. стр. 202–233. ISBN 978-1-4675-7992-6 . Архивировано из оригинала 17 января 2023 года . Проверено 7 апреля 2017 г.
- ^ Уильямс, Мэтт (28 января 2022 г.). «Что такое теория относительности Эйнштейна?» . Вселенная сегодня . Архивировано из оригинала 3 августа 2022 года . Проверено 13 августа 2022 г. .
- ^ Стэйчел, Джон (2005). «Коэффициент Френеля (перетаскивания) как вызов оптике движущихся тел XIX века». (PDF) . В Коксе, Эй Джей; Эйзенштадт, Жан (ред.). Вселенная общей теории относительности . Бостон, Массачусетс: Биркхойзер. стр. 1–13. ISBN 0-8176-4380-Х . Архивировано из оригинала (PDF) 15 апреля 2017 года.
- ^ «Джордж Фрэнсис Фитцджеральд» . Библиотека Линды Холл . Архивировано из оригинала 17 января 2023 года . Проверено 13 августа 2022 г. .
- ^ «Нобелевская премия по физике 1902 года» . NobelPrize.org . Архивировано из оригинала 23 июня 2017 года . Проверено 13 августа 2022 г. .
- ^ Jump up to: Перейти обратно: а б с Паис, Авраам (1982). «Тонок Господь…»: Наука и жизнь Альберта Эйнштейна (11-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 0-19-853907-Х .
- ^ Дарригол, О. (2005), «Происхождение теории относительности» (PDF) , Séminaire Poincaré , 1 : 1–22, Бибкод : 2006eins.book....1D , doi : 10.1007/3-7643-7436 -5_1 , ISBN 978-3-7643-7435-8 , заархивировано (PDF) из оригинала 28 февраля 2008 г. , получено 17 июля 2017 г.
- ^ Миллер, Артур И. (1998). Специальная теория относительности Альберта Эйнштейна . Нью-Йорк: Springer-Verlag. ISBN 0-387-94870-8 .
- ^ Jump up to: Перейти обратно: а б с Галисон, Питер (2003). Часы Эйнштейна, Карты Пуанкаре: Империи времени . Нью-Йорк: WW Norton & Company, Inc., стр. 13–47 . ISBN 0-393-02001-0 .
- ^ Пуанкаре, Анри (1906). «О динамике электрона (Sur la dynamice de l'électron)» . Rendiconti del Circolo Matematico di Palermo . 21 : 129–176. Бибкод : 1906RCMP...21..129P . дои : 10.1007/bf03013466 . hdl : 2027/uiug.30112063899089 . S2CID 120211823 . Архивировано из оригинала 11 июля 2017 года . Проверено 15 июля 2017 г.
- ^ Захар, Эли (1989) [1983], «Независимое открытие Пуанкаре принципа относительности», Революция Эйнштейна: исследование эвристики , Чикаго, Иллинойс: Издательство Open Court Publishing Company, ISBN 0-8126-9067-2
- ^ Jump up to: Перейти обратно: а б Уолтер, Скотт А. (2007). «Прорыв в 4-векторы: четырехмерное движение в гравитации, 1905–1910» . В Ренне, Юрген; Шеммель, Матиас (ред.). Генезис общей теории относительности, том 3 . Берлин, Германия: Шпрингер. стр. 193–252. Архивировано из оригинала 28 мая 2024 года . Проверено 15 июля 2017 г.
- ^ Эйнштейн, Альберт (1905). «К электродинамике движущихся тел» . Анналы физики . 322 (10): 891–921. Бибкод : 1905АнП...322..891Е . дои : 10.1002/andp.19053221004 . Архивировано из оригинала 6 ноября 2018 года . Проверено 7 апреля 2018 г.
- ^ Исааксон, Уолтер (2007). Эйнштейн: Его жизнь и Вселенная . Саймон и Шустер. стр. 26–27, 122–127, 145–146, 345–349, 448–460. ISBN 978-0-7432-6473-0 .
- ^ Jump up to: Перейти обратно: а б Вайнштейн, Галина (2012). «Макс Борн, Альберт Эйнштейн и пространственно-временной формализм специальной теории относительности Германа Минковского». arXiv : 1210.6929 [ physical.hist-ph ].
- ^ Галисон, Питер Луи (1979). «Пространство-время Минковского: от визуального мышления к абсолютному миру». Исторические исследования в области физических наук . 10 : 85–121. дои : 10.2307/27757388 . JSTOR 27757388 .
- ^ Jump up to: Перейти обратно: а б Минковский, Герман (1909). «Пространство и время» [Пространство и время]. Годовой отчет Немецкой ассоциации математиков . Б. Г. Тойбнер: 1-14. Архивировано из оригинала 28 июля 2017 года . Проверено 17 июля 2017 г.
- ^ Jump up to: Перейти обратно: а б Картан, Э.; Фано, Г. (1955) [1915]. «Теория непрерывных групп и геометрии» . Энциклопедия чистых и прикладных математических наук . 3 (1): 39–43. Архивировано из оригинала 23 марта 2018 года . Проверено 6 апреля 2018 г. (В 1915 году были опубликованы только страницы 1–21, вся статья, включая стр. 39–43, касающуюся групп Лагерра и Лоренца, была посмертно опубликована в 1955 году в сборнике статей Картана и переиздана в Энциклопедии в 1991 году.)
- ^ Каструп, Х.А. (2008). «О достижениях конформных преобразований и связанных с ними симметрий в геометрии и теоретической физике». Аннален дер Физик . 520 (9–10): 631–690. arXiv : 0808.2730 . Бибкод : 2008АнП...520..631К . дои : 10.1002/andp.200810324 . S2CID 12020510 .
- ^ Рэтклифф, Дж. Г. (1994). «Гиперболическая геометрия» . Основы гиперболических многообразий . Нью-Йорк. стр. 56–104 . ISBN 0-387-94348-Х .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Jump up to: Перейти обратно: а б с д и Когут, Джон Б. (2001). Введение в теорию относительности . Массачусетс: Harcourt/Academic Press. ISBN 0-12-417561-9 .
- ^ Рэй д'Инверно; Джеймс Викерс (2022). Знакомство с теорией относительности Эйнштейна: более глубокое понимание (иллюстрированное издание). Издательство Оксфордского университета. стр. 26–28. ISBN 978-0-19-886202-4 . Выдержка со страницы 27
- ^ Ландау, Л.Д. и Лифшиц, Э.М. (2013). Классическая теория полей (Том 2).
- ^ Кэрролл, Шон (2022). Величайшие идеи во Вселенной . Нью-Йорк: ООО «Пингвин Рэндом Хаус». стр. 155–156. ISBN 9780593186589 .
- ^ Куриэль, Эрик; Бокулич, Петр. «Световые конусы и причинная структура» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. Архивировано из оригинала 17 мая 2019 года . Проверено 26 марта 2017 г.
- ^ Jump up to: Перейти обратно: а б Савитт, Стивен. «Бытие и становление в современной физике. 3. Специальная теория относительности» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. Архивировано из оригинала 11 марта 2017 года . Проверено 26 марта 2017 г.
- ^ Jump up to: Перейти обратно: а б с д и ж Шютц, Бернард Ф. (1985). Первый курс общей теории относительности . Кембридж, Великобритания: Издательство Кембриджского университета. п. 26. ISBN 0-521-27703-5 .
- ^ Jump up to: Перейти обратно: а б с д и ж г Вайс, Майкл. «Парадокс близнецов» . Часто задаваемые вопросы по физике и теории относительности . Архивировано из оригинала 27 апреля 2017 года . Проверено 10 апреля 2017 г. .
- ^ Молд, Ричард А. (1994). Основная теория относительности (1-е изд.). Спрингер. п. 42. ИСБН 978-0-387-95210-9 . Проверено 22 апреля 2017 г.
- ^ Лернер, Лоуренс С. (1997). Физика для ученых и инженеров, Том 2 (1-е изд.). Паб «Джонс и Бартлетт». п. 1047. ИСБН 978-0-7637-0460-5 . Проверено 22 апреля 2017 г.
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н тот Байс, Сандер (2007). Совершенно специальная теория относительности: иллюстрированное руководство . Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN 978-0-674-02611-7 .
- ^ Форшоу, Джеффри; Смит, Гэвин (2014). Динамика и относительность . Джон Уайли и сыновья. п. 118. ИСБН 978-1-118-93329-9 . Проверено 24 апреля 2017 г. .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н тот п д Морен, Дэвид (2017). Специальная теория относительности для начинающих энтузиастов . Независимая издательская платформа CreateSpace. ISBN 978-1-5423-2351-2 .
- ^ Ландау, Л.Д.; Лифшиц, Э.М. (2006). Классическая теория поля, Курс теоретической физики, Том 2 (4-е изд.). Амстердам: Эльзевир. стр. 1–24. ISBN 978-0-7506-2768-9 .
- ^ Jump up to: Перейти обратно: а б Морен, Дэвид (2008). Введение в классическую механику: с задачами и решениями . Издательство Кембриджского университета. ISBN 978-0-521-87622-3 .
- ^ Роуз, HH (21 апреля 2008 г.). «Оптика высокопроизводительных электронных микроскопов» . Наука и технология перспективных материалов . 9 (1): 014107. Бибкод : 2008STAdM...9a4107R . дои : 10.1088/0031-8949/9/1/014107 . ПМК 5099802 . ПМИД 27877933 .
- ^ Гриффитс, Дэвид Дж. (2013). Революции в физике двадцатого века . Кембридж: Издательство Кембриджского университета. п. 60. ИСБН 978-1-107-60217-5 . Проверено 24 мая 2017 г.
- ^ Байерс, Нина (1998). «Открытие Э. Нётер глубокой связи между симметриями и законами сохранения». arXiv : физика/9807044 .
- ^ Нейв, Р. «Энергетика распада заряженного пиона» . Гиперфизика . Кафедра физики и астрономии Университета штата Джорджия. Архивировано из оригинала 21 мая 2017 года . Проверено 27 мая 2017 г.
- ^ Томас, Джордж Б.; Вейр, Морис Д.; Хасс, Джоэл; Джордано, Фрэнк Р. (2008). Исчисление Томаса: ранние трансценденталии (одиннадцатое изд.). Бостон: Pearson Education, Inc., с. 533. ИСБН 978-0-321-49575-4 .
- ^ Тейлор, Эдвин Ф.; Уиллер, Джон Арчибальд (1992). Физика пространства-времени (2-е изд.). У. Х. Фриман. ISBN 0-7167-2327-1 .
- ^ Э.Дж. Пост (1962). Формальная структура электромагнетизма: общая ковариация и электромагнетизм . Dover Publications Inc. ISBN 978-0-486-65427-0 .
- ^ Jump up to: Перейти обратно: а б Гиббс, Филип. «Может ли специальная теория относительности справиться с ускорением?» . Часто задаваемые вопросы по физике и теории относительности . math.ucr.edu. Архивировано из оригинала 7 июня 2017 года . Проверено 28 мая 2017 г.
- ^ Франклин, Джерролд (2010). «Лоренцево сокращение, космические корабли Белла и движение твердого тела в специальной теории относительности». Европейский журнал физики . 31 (2): 291–298. arXiv : 0906.1919 . Бибкод : 2010EJPh...31..291F . дои : 10.1088/0143-0807/31/2/006 . S2CID 18059490 .
- ^ Лоренц, ХА; Эйнштейн, А.; Минковский, Х.; Вейль, Х. (1952). Принцип относительности: Сборник оригинальных мемуаров по специальной и общей теории относительности . Дуврские публикации. ISBN 0-486-60081-5 .
- ^ Jump up to: Перейти обратно: а б с Мук, Дело Э.; Варгиш, Тома (1987). Внутри теории относительности . Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN 0-691-08472-6 .
- ^ Местер, Джон. «Экспериментальные проверки общей теории относительности» (PDF) . Laboratoire Univers et Théories. Архивировано из оригинала (PDF) 18 марта 2017 года . Проверено 9 июня 2017 г.
- ^ Jump up to: Перейти обратно: а б Кэрролл, Шон М. (2 декабря 1997 г.). «Конспекты лекций по общей теории относительности». arXiv : gr-qc/9712019 .
- ^ Леверье, Урбен (1859). «Письмо г-на Леверье г-ну Фэю о теории Меркурия и о движении перигелия этой планеты» . Еженедельные отчеты сессий Академии наук . 49 : 379–383.
- ^ Уорролл, Саймон (4 ноября 2015 г.). «Охота на Вулкан, планету, которой не было» . Нэшнл Географик . Архивировано из оригинала 24 мая 2017 года.
- ^ Левин, Алайна Г. (май 2016 г.). «29 мая 1919 года: Эддингтон наблюдает солнечное затмение, чтобы проверить общую теорию относительности» . Этот месяц в истории физики. Новости АПС . Американское физическое общество. Архивировано из оригинала 2 июня 2017 года.
- ^ Jump up to: Перейти обратно: а б Хобсон, член парламента; Эфстатиу, Г.; Ласенби, АН (2006). Общая теория относительности . Кембридж: Издательство Кембриджского университета. стр. 176–179. ISBN 978-0-521-82951-9 .
- ^ Торн, Кип С. (1988). Фэрбанк, JD; Дивер, Б.С. младший; Эверитт, ВФ; Майкельсон, П.Ф. (ред.). Около нуля: новые рубежи физики (PDF) . WH Фриман и компания. стр. 573–586. S2CID 12925169 . Архивировано из оригинала (PDF) 28 июля 2017 года.
- ^ Фейнман, Р.П.; Лейтон, РБ; Сэндс, М. (1964). Фейнмановские лекции по физике, том. 2 (изд. Нового Тысячелетия). Основные книги. стр. 13–6–13–11. ISBN 978-0-465-02416-2 . Архивировано из оригинала 17 января 2023 года . Проверено 1 июля 2017 года .
- ^ Уильямс, РК (1995). «Извлечение рентгеновских лучей, Ύ-лучей и релятивистских e − -и + пары из сверхмассивных черных дыр Керра с использованием механизма Пенроуза». Physical Review D. 51 ( 10): 5387–5427. Bibcode : 1995PhRvD..51.5387W . doi : 10.1103/PhysRevD.51.5387 . PMID 10018300 .
- ^ Уильямс, РК (2004). «Коллимированный уходящий вихревой полярный e − -и + струи, по своей природе порождаемые вращающимися черными дырами и процессами Пенроуза». The Astrophysical Journal . 611 (2): 952–963. arXiv : astro-ph/0404135 . Bibcode : 2004ApJ...611..952W . doi : 10.1086/422304 . S2CID 1350543 .
- ^ Курода, Таками; Котаке, Кей; Такиваки, Томоя (2012). «Полностью общерелятивистское моделирование сверхновых с коллапсом ядра с приближенным транспортом нейтрино». Астрофизический журнал . 755 (1): 11. arXiv : 1202.2487 . Бибкод : 2012ApJ...755...11K . дои : 10.1088/0004-637X/755/1/11 . S2CID 119179339 .
- ^ Воллак, Эдвард Дж. (10 декабря 2010 г.). «Космология: Исследование Вселенной» . Вселенная 101: Теория большого взрыва . НАСА . Архивировано из оригинала 14 мая 2011 года . Проверено 15 апреля 2017 г.
- ^ Jump up to: Перейти обратно: а б Бонди, Герман (1957). ДеВитт, Сесиль М.; Риклз, Дин (ред.). Роль гравитации в физике: отчет с конференции в Чапел-Хилл 1957 года . Берлин, Германия: Исследовательская библиотека Макса Планка. стр. 159–162. ISBN 978-3-86931-963-6 . Архивировано из оригинала 28 июля 2017 года . Проверено 1 июля 2017 года .
- ^ Кроуэлл, Бенджамин (2000). Общая теория относительности . Фуллертон, Калифорния: Свет и материя. стр. 241–258. Архивировано из оригинала 18 июня 2017 года . Проверено 30 июня 2017 г.
- ^ Кройцер, Л.Б. (1968). «Экспериментальное измерение эквивалентности активной и пассивной гравитационной массы». Физический обзор . 169 (5): 1007–1011. Бибкод : 1968PhRv..169.1007K . дои : 10.1103/PhysRev.169.1007 .
- ^ Уилл, СМ (1976). «Активная масса в релятивистской гравитационно-теоретической интерпретации эксперимента Крейцера» . Астрофизический журнал . 204 : 224–234. Бибкод : 1976ApJ...204..224W . дои : 10.1086/154164 . Архивировано из оригинала 28 сентября 2018 года . Проверено 2 июля 2017 г.
- ^ Бартлетт, DF; Ван Бюрен, Дэйв (1986). «Эквивалентность активной и пассивной гравитационной массы с использованием Луны». Письма о физических отзывах . 57 (1): 21–24. Бибкод : 1986PhRvL..57...21B . doi : 10.1103/PhysRevLett.57.21 . ПМИД 10033347 .
- ^ Сингх, Вишва Виджай; Мюллер, Юрген; Бискупек, Лилиан; Хакманн, Ева; Леммерцаль, Клаус (2023). «Эквивалентность активной и пассивной гравитационной массы проверена с помощью лунной лазерной локации» . Письма о физических отзывах . 131 (2): 021401. arXiv : 2212.09407 . Бибкод : 2023PhRvL.131b1401S . doi : 10.1103/PhysRevLett.131.021401 . ПМИД 37505941 . Проверено 7 марта 2024 г.
- ^ «Гравитационный зонд Б: Часто задаваемые вопросы» . Архивировано из оригинала 2 июня 2018 года . Проверено 2 июля 2017 г.
- ^ Гульотта, Г. (16 февраля 2009 г.). «Настойчивость окупается при проверке теории относительности в космосе» . Нью-Йорк Таймс . Архивировано из оригинала 3 сентября 2018 года . Проверено 2 июля 2017 г.
- ^ Эверитт, CWF; Паркинсон, BW (2009). «Научные результаты гравитационного зонда B — итоговый отчет НАСА» (PDF) . Архивировано (PDF) из оригинала 23 октября 2012 года . Проверено 2 июля 2017 г.
- ^ Эверитт; и др. (2011). «Гравитационный зонд B: окончательные результаты космического эксперимента по проверке общей теории относительности». Письма о физических отзывах . 106 (22): 221101. arXiv : 1105.3456 . Бибкод : 2011PhRvL.106v1101E . doi : 10.1103/PhysRevLett.106.221101 . ПМИД 21702590 . S2CID 11878715 .
- ^ Чуфолини, Игнацио; Паолоцци, Антонио Рольф Кениг; Павлис, Эррикос К.; Кениг, Рольф (2016). «Проверка общей теории относительности с использованием спутников LARES и LAGEOS и гравитационной модели Земли GRACE» . Европейский физический журнал C . 76 (3): 120. arXiv : 1603.09674 . Бибкод : 2016EPJC...76..120C . doi : 10.1140/epjc/s10052-016-3961-8 . ПМЦ 4946852 . ПМИД 27471430 .
- ^ Иорио, Л. (февраль 2017 г.). «Комментарий к статье «Проверка общей теории относительности с использованием спутников LARES и LAGEOS и гравитационной модели Земли GRACE. Измерение увлечения Земли инерциальными системами отсчета», И. Чуфолини и др.». Европейский физический журнал C . 77 (2): 73. arXiv : 1701.06474 . Бибкод : 2017EPJC...77...73I . дои : 10.1140/epjc/s10052-017-4607-1 . S2CID 118945777 .
- ^ Картлидж, Эдвин (20 января 2016 г.). «Подземные кольцевые лазеры проверят общую теорию относительности» . Physicsworld.com . Институт физики. Архивировано из оригинала 12 июля 2017 года . Проверено 2 июля 2017 г.
- ^ «Эйнштейн прав, используя самые чувствительные из когда-либо созданных датчиков вращения Земли» . Физика.орг . Сеть Science X. Архивировано из оригинала 10 мая 2017 года . Проверено 2 июля 2017 г.
- ^ Мурзи, Мауро. «Жюль Анри Пуанкаре (1854–1912)» . Интернет-энциклопедия философии (ISSN 2161-0002). Архивировано из оригинала 23 декабря 2020 года . Проверено 9 апреля 2018 г.
- ^ Дезер, С. (1970). «Самовзаимодействие и калибровочная инвариантность». Общая теория относительности и гравитация . 1 (18): 9–8. arXiv : gr-qc/0411023 . Бибкод : 1970GReGr...1....9D . дои : 10.1007/BF00759198 . S2CID 14295121 .
- ^ Грищук, Л.П.; Петров, АН; Попова, А.Д. (1984). «Точная теория гравитационного поля (Эйнштейна) в произвольном фоновом пространстве-времени» . Связь в математической физике . 94 (3): 379–396. Бибкод : 1984CMaPh..94..379G . дои : 10.1007/BF01224832 . S2CID 120021772 . Архивировано из оригинала 25 февраля 2021 года . Проверено 9 апреля 2018 г.
- ^ Розен, Н. (1940). «Общая теория относительности и плоское пространство I». Физический обзор . 57 (2): 147–150. Бибкод : 1940PhRv...57..147R . дои : 10.1103/PhysRev.57.147 .
- ^ Вайнберг, С. (1964). «Вывод калибровочной инвариантности и принципа эквивалентности из лоренц-инвариантности S-матрицы». Письма по физике . 9 (4): 357–359. Бибкод : 1964PhL.....9..357W . дои : 10.1016/0031-9163(64)90396-8 .
- ^ Jump up to: Перейти обратно: а б Торн, Кип (1995). Черные дыры и деформации времени: возмутительное наследие Эйнштейна . WW Нортон и компания. ISBN 978-0-393-31276-8 .
- ^ Бонди, Х.; Ван дер Бург, MGJ; Мецнер, А. (1962). «Гравитационные волны в общей теории относительности: VII. Волны из осесимметричных изолированных систем». Труды Лондонского королевского общества А. А269 (1336): 21–52. Бибкод : 1962RSPSA.269...21B . дои : 10.1098/rspa.1962.0161 . S2CID 120125096 .
- ^ Сакс, Райнер К. (1962). «Асимптотические симметрии в теории гравитации». Физический обзор . 128 (6): 2851–2864. Бибкод : 1962PhRv..128.2851S . дои : 10.1103/PhysRev.128.2851 .
- ^ Jump up to: Перейти обратно: а б Строминджер, Эндрю (2017). «Лекции по инфракрасной структуре гравитации и калибровочной теории». arXiv : 1703.05448 [ hep-th ].
...отредактированная стенограмма курса, прочитанного автором в Гарварде в весеннем семестре 2016 года. Он содержит педагогический обзор последних разработок, связывающих темы мягких теорем, эффекта памяти и асимптотических симметрий в четырехмерной КЭД, неабелевой калибровочной теории и гравитация с приложениями к черным дырам. Будет опубликовано Princeton University Press, 158 страниц.
- ^ maths.tcd.ie
- ^ Jump up to: Перейти обратно: а б с д Бэр, Кристиан; Фреденхаген, Клаус (2009). «Лоренцевы многообразия» (PDF) . Квантовая теория поля в искривленном пространстве-времени: концепции и математические основы . Дордрехт: Спрингер. стр. 39–58. ISBN 978-3-642-02779-6 . Архивировано из оригинала (PDF) 15 апреля 2017 года . Проверено 14 апреля 2017 г.
- ^ Тегмарк, Макс (1 апреля 1997 г.). «О размерности пространства-времени». Классическая и квантовая гравитация . 14 (4): Л69–Л75. arXiv : gr-qc/9702052 . Бибкод : 1997CQGra..14L..69T . дои : 10.1088/0264-9381/14/4/002 . ISSN 0264-9381 . S2CID 250904081 .
- ^ Скоу, Брэдфорд (2007). «Чем время отличается от пространства?» (PDF) . Нус . 41 (2): 227–252. CiteSeerX 10.1.1.404.7853 . дои : 10.1111/j.1468-0068.2007.00645.x . Архивировано из оригинала (PDF) 24 августа 2016 года . Проверено 13 апреля 2018 г.
- ^ Лейбниц, Готфрид (1880). «Рассуждения о метафизике» . Философские сочинения Готфрида Вильгельма Лейбница . Том 4. Вайдман. стр. 427–463 . Проверено 13 апреля 2018 г.
- ^ Эренфест, Пауль (1920). «Какую роль трехмерность пространства играет в основных законах физики?» [Как фундаментальные законы физики подтверждают, что пространство имеет три измерения?]. Анналы физики . 61 (5): 440–446. Бибкод : 1920АнП...366..440Е . дои : 10.1002/andp.19203660503 . . См. также Эренфест П. (1917) «Как в фундаментальных законах физики проявляется трехмерность пространства?» Труды Амстердамской академии 20:200.
- ^ Вейль, Х. (1922). Пространство, время и материя . Дуврская перепечатка: 284.
- ^ Тангерлини, Франция (1963). «Поле Шварцшильда в n измерениях и проблема размерности пространства». Нуово Чименто . 27 (3): 636–651. Бибкод : 1963NCim...27..636T . дои : 10.1007/BF02784569 . S2CID 119683293 .
- ^ Jump up to: Перейти обратно: а б с Тегмарк, Макс (апрель 1997 г.). «О размерности пространства-времени» (PDF) . Классическая и квантовая гравитация . 14 (4): Л69–Л75. arXiv : gr-qc/9702052 . Бибкод : 1997CQGra..14L..69T . дои : 10.1088/0264-9381/14/4/002 . S2CID 15694111 . Проверено 16 декабря 2006 г.
- ^ Фэн, Западная X (3 августа 2022 г.). «Гравотермический фазовый переход, черные дыры и размерность пространства» . Физический обзор D . 106 (4): L041501. arXiv : 2207.14317 . Бибкод : 2022PhRvD.106d1501F . doi : 10.1103/PhysRevD.106.L041501 . S2CID 251196731 .
- ^ Скаргилл, JHC (26 февраля 2020 г.). «Существование жизни в 2+1 измерениях» . Обзор физических исследований . 2 (1): 013217. arXiv : 1906.05336 . Бибкод : 2020PhRvR...2a3217S . doi : 10.1103/PhysRevResearch.2.013217 . S2CID 211734117 .
- ^ «Жизнь может существовать в 2D-вселенной (во всяком случае, согласно физике)» . Technologyreview.com . Проверено 16 июня 2021 г.
Дальнейшее чтение [ править ]
- Барроу, Джон Д .; Типлер, Фрэнк Дж. (1986). Антропный космологический принцип (1-е изд.). Издательство Оксфордского университета . ISBN 978-0-19-282147-8 . LCCN 87028148 .
- Джордж Ф. Эллис и Рут М. Уильямс (1992) Плоское и искривленное пространство-время . Издательство Оксфордского университета. ISBN 0-19-851164-7
- Лоренц, Х.А. , Эйнштейн, Альберт , Минковский, Герман и Вейль, Герман (1952) Принцип относительности: Сборник оригинальных мемуаров . Дувр.
- Лукас, Джон Рэндольф (1973) Трактат о времени и пространстве . Лондон: Метуэн.
- Пенроуз, Роджер (2004). Дорога к реальности . Оксфорд: Издательство Оксфордского университета. ISBN 0-679-45443-8 . Главы 17–18.
- Тейлор, EF; Уилер, Джон А. (1992). Физика пространства-времени, второе издание . Интернет-архив: WH Freeman. ISBN 0-7167-2327-1 .
- Аркани-Хамед, Нима (1 декабря 2017 г.). Гибель пространства-времени: почему оно должно раствориться в более фундаментальных структурах (речь). 2384-е собрание Общества. Вашингтон, округ Колумбия . Проверено 16 июля 2022 г.
Внешние ссылки [ править ]
 СМИ, связанные с пространством-временем, на Викискладе?
СМИ, связанные с пространством-временем, на Викискладе? - Альберт Эйнштейн о пространстве-времени. 13-е издание Британской исторической энциклопедии: статья Альберта Эйнштейна 1926 года.
- Энциклопедия пространства-времени и гравитации Наука Экспертные статьи
- Стэнфордская энциклопедия философии : « Пространство и время: инерциальные рамки » Роберта ДиСалле.









































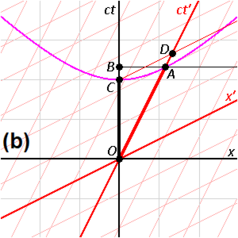






























































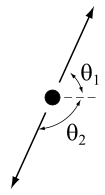





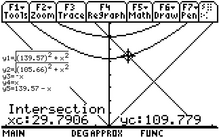


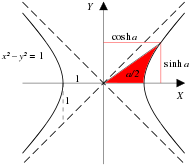


































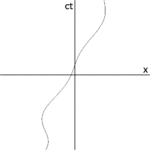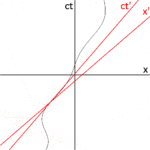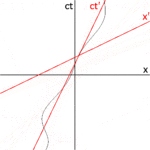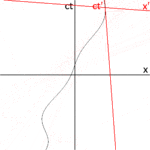









































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2 }+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)

























