Гравитационное поле

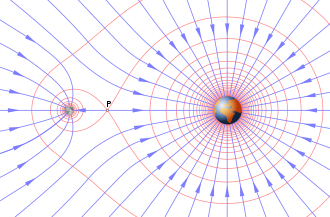
Изображение гравитационного поля Земли и Луны вместе (не в масштабе). Векторное поле (синее) и связанное с ним скалярное потенциальное поле (красное). Точка P между Землей и Луной является точкой равновесия .

В физике гравитационное поле или поле гравитационного ускорения — это векторное поле, используемое для объяснения влияний, с которыми тело распространяется в пространство вокруг себя. ^[1] Гравитационное поле используется для объяснения гравитационных явлений, таких как гравитационных сил, поле действующее на другое массивное тело. Имеет размерность ускорения ( L /T ²) и измеряется в единицах ньютонов в на килограмм (Н/кг) или, что то же самое, в метрах на секунду квадрате (м/с ²).

В своей первоначальной концепции гравитация представляла собой силу между точечными массами . Вслед за Исааком Ньютоном Пьер -Симон Лаплас попытался смоделировать гравитацию как своего рода радиационное поле или жидкость , и с XIX века объяснения гравитации в классической механике обычно преподаются в терминах модели поля, а не точечного притяжения. Это результат пространственного градиента гравитационного потенциального поля .

В общей теории относительности , а не две частицы, притягивающие друг друга, частицы искажают пространство-время посредством своей массы, и это искажение воспринимается и измеряется как «сила». ^{[ нужна ссылка ]} В такой модели утверждается, что материя движется определенным образом в ответ на искривление пространства-времени. ^[2] и что гравитационной силы либо нет , ^[3] или что гравитация — это фиктивная сила . ^[4]

Гравитация отличается от других сил соблюдением принципа эквивалентности .

Классическая механика

В классической механике гравитационное поле является физической величиной. ^[5] Гравитационное поле можно определить с помощью закона всемирного тяготения Ньютона . Определенное таким образом гравитационное поле $g$ вокруг отдельной частицы массы $M$ представляет собой векторное поле, состоящее в каждой точке из вектора, направленного непосредственно к частице. Величина поля в каждой точке рассчитывается с применением универсального закона и представляет собой силу на единицу массы, действующую на любой объект в этой точке пространства. Поскольку силовое поле консервативно, существует скалярная потенциальная энергия на единицу массы $Φ$ в каждой точке пространства, связанной с силовыми полями; это называется гравитационным потенциалом . ^[6] Уравнение гравитационного поля имеет вид ^[7] $\mathbf {g} ={\frac {\mathbf {F} }{m}}={\frac {d^{2}\mathbf {R} }{dt^{2}}}=-GM{\frac {\mathbf {R} }{\left|\mathbf {R} \right|^{3}}}=-\nabla \Phi ,$ где $F$ — гравитационная сила , $m$ — масса пробной частицы , $R$ — радиальный вектор пробной частицы относительно массы (или для второго закона движения Ньютона, который является функцией, зависящей от времени, набором положений пробной частицы частицы, каждая из которых занимает определенную точку пространства на момент начала тестирования), $t$ — время , $G$ — гравитационная постоянная , а $\nabla$ — оператор del .

Сюда входит закон всемирного тяготения Ньютона и связь между гравитационным потенциалом и ускорением поля. $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ d 2 Р / д т 2 ⁠$ и $⁠ F / m ⁠$ оба равны гравитационному ускорению $g$ (эквивалентно ускорению инерции, имеет ту же математическую форму, но также определяется как гравитационная сила на единицу массы). ^[8]). Отрицательные знаки вставлены, поскольку сила действует антипараллельно смещению. Эквивалентное уравнение поля в терминах плотности $массы ρ$ притягивающей массы: $\nabla \cdot \mathbf {g} =-\nabla ^{2}\Phi =-4\pi G\rho$ который содержит закон Гаусса для гравитации и уравнение Пуассона для гравитации . Закон Ньютона подразумевает закон Гаусса, но не наоборот; см. Связь между законами Гаусса и Ньютона .

Эти классические уравнения представляют собой дифференциальные уравнения движения пробной частицы в присутствии гравитационного поля, т.е. составление и решение этих уравнений позволяет определить и описать движение пробной массы.

Поле вокруг нескольких частиц — это просто векторная сумма полей вокруг каждой отдельной частицы. Пробная частица в таком поле будет испытывать силу, равную векторной сумме сил, которые она испытала бы в этих отдельных полях. Это ^[9] $\mathbf {g} =\sum _{i}\mathbf {g} _{i}={\frac {1}{m}}\sum _{i}\mathbf {F} _{i}=-G\sum _{i}m_{i}{\frac {\mathbf {R} -\mathbf {R} _{i}}{\left|\mathbf {R} -\mathbf {R} _{i}\right|^{3}}}=-\sum _{i}\nabla \Phi _{i},$ т.е. гравитационное поле массы $m j$ представляет собой сумму всех гравитационных полей, возникающих из-за всех других масс m _i , кроме самой массы $m j$ . $R i$ — вектор положения гравитирующей частицы $i$ , а $R$ — вектор положения пробной частицы.

Общая теория относительности

В общей теории относительности символы Кристоффеля играют роль гравитационного силового поля, а метрический тензор играет роль гравитационного потенциала.

В общей теории относительности гравитационное поле определяется путем решения уравнений поля Эйнштейна. ^[10] $\mathbf {G} =\kappa \mathbf {T} ,$ где $T$ — тензор энергии-импульса , $G$ — тензор Эйнштейна , а $κ$ — гравитационная постоянная Эйнштейна . Последний определяется как $κ = 8 πG / c 4$ , где $G$ — гравитационная постоянная Ньютона , а $c$ — скорость света .

Эти уравнения зависят от распределения материи, напряжения и импульса в определенной области пространства, в отличие от ньютоновской гравитации, которая зависит только от распределения материи. Сами поля в общей теории относительности представляют собой искривление пространства-времени. что пребывание в области искривленного пространства эквивалентно ускорению утверждает , градиента Общая теория относительности поля. Согласно второму закону Ньютона , это заставит объект испытывать фиктивную силу , если он будет неподвижен по отношению к полю. Вот почему человек, стоя на месте на поверхности Земли, будет чувствовать себя притянутым вниз силой гравитации. В целом гравитационные поля, предсказанные общей теорией относительности, лишь незначительно отличаются по своим эффектам от тех, которые предсказываются классической механикой, но существует ряд легко проверяемых различий , одно из наиболее известных — отклонение света в таких полях.

Диаграмма встраивания

Диаграммы встраивания — это трехмерные графики, обычно используемые для образовательной иллюстрации гравитационного потенциала путем рисования полей гравитационного потенциала в виде гравитационной топографии, изображающей потенциалы в виде так называемых гравитационных колодцев , сферы влияния .

См. также

Ссылки

^ Фейнман, Ричард (1970). Фейнмановские лекции по физике . Том. I. Аддисон Уэсли Лонгман. ISBN 978-0-201-02115-8 .
^ Герох, Роберт (1981). Общая теория относительности от А до Б. Издательство Чикагского университета . п. 181. ИСБН 978-0-226-28864-2 .
^ Грин, Эйвинд; Хервик, Сигбьёрн (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии . Спрингер Япония. стр. 256. ISBN 978-0-387-69199-2 .
^ Фостер, Дж.; Найтингейл, Джей Ди (2006). Краткий курс общей теории относительности (3-е изд.). Спрингер Наука и бизнес. п. 55. ИСБН 978-0-387-26078-5 .
^ Фейнман, Ричард (1970). Фейнмановские лекции по физике . Том. II. Эддисон Уэсли Лонгман. ISBN 978-0-201-02115-8 . «Поле» — это любая физическая величина, принимающая разные значения в разных точках пространства.
^ Форшоу, младший; Смит, АГ (2009). Динамика и относительность . Уайли. ISBN 978-0-470-01460-8 . ^{[ нужна страница ]}
^ Лернер, Р.Г. ; Тригг, Г.Л., ред. (1991). Энциклопедия физики (2-е изд.). Вайли-ВЧ . ISBN 978-0-89573-752-6 . п. 451
^ Уилан, премьер-министр; Ходжсон, MJ (1978). Основные принципы физики (2-е изд.). Джон Мюррей. ISBN 978-0-7195-3382-2 . ^{[ нужна страница ]}
^ Киббл, TWB (1973). Классическая механика . Европейская серия по физике (2-е изд.). Великобритания: МакГроу Хилл . ISBN 978-0-07-084018-8 . ^{[ нужна страница ]}
^ Уиллер, Дж.А.; Миснер, К.; Торн, Канзас (1973). Гравитация . WH Freeman & Co. с. 404. ИСБН 978-0-7167-0344-0 .

[1] Фейнман, Ричард (1970). Фейнмановские лекции по физике . Том. I. Аддисон Уэсли Лонгман. ISBN 978-0-201-02115-8 .

[2] Герох, Роберт (1981). Общая теория относительности от А до Б. Издательство Чикагского университета . п. 181. ИСБН 978-0-226-28864-2 .

[3] Грин, Эйвинд; Хервик, Сигбьёрн (2007). Общая теория относительности Эйнштейна: с современными приложениями в космологии . Спрингер Япония. стр. 256. ISBN 978-0-387-69199-2 .

[4] Фостер, Дж.; Найтингейл, Джей Ди (2006). Краткий курс общей теории относительности (3-е изд.). Спрингер Наука и бизнес. п. 55. ИСБН 978-0-387-26078-5 .

[5] Фейнман, Ричард (1970). Фейнмановские лекции по физике . Том. II. Эддисон Уэсли Лонгман. ISBN 978-0-201-02115-8 . «Поле» — это любая физическая величина, принимающая разные значения в разных точках пространства.

[6] Форшоу, младший; Смит, АГ (2009). Динамика и относительность . Уайли. ISBN 978-0-470-01460-8 . ^{[ нужна страница ]}

[7] Лернер, Р.Г. ; Тригг, Г.Л., ред. (1991). Энциклопедия физики (2-е изд.). Вайли-ВЧ . ISBN 978-0-89573-752-6 . п. 451

[8] Уилан, премьер-министр; Ходжсон, MJ (1978). Основные принципы физики (2-е изд.). Джон Мюррей. ISBN 978-0-7195-3382-2 . ^{[ нужна страница ]}

[9] Киббл, TWB (1973). Классическая механика . Европейская серия по физике (2-е изд.). Великобритания: МакГроу Хилл . ISBN 978-0-07-084018-8 . ^{[ нужна страница ]}

[10] Уиллер, Дж.А.; Миснер, К.; Торн, Канзас (1973). Гравитация . WH Freeman & Co. с. 404. ИСБН 978-0-7167-0344-0 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]