Гравитационная постоянная

Не путать с g , гравитацией Земли .

Значение G	Единица
6.674 30 (15) × 10 −11	N ⋅ m 2 ⋅ kg −2
6.674 30 (15) × 10 −8	dyn ⋅ cm 2 ⋅ g −2
4.300 917 2706 (3) × 10 −3	pc ⋅ M ⊙ −1 ⋅( км / с ) 2

Гравитационная постоянная G является ключевой величиной в законе всемирного тяготения Ньютона .

Гравитационная постоянная – это эмпирическая физическая константа, используемая при расчете гравитационных эффектов в сэра Исаака Ньютона и законе всемирного тяготения в Альберта Эйнштейна общей теории относительности . Она также известна как универсальная гравитационная постоянная , гравитационная постоянная Ньютона или гравитационная постоянная Кавендиша . обозначается заглавной Г. буквой

В законе Ньютона это константа пропорциональности, связывающая силу гравитации между двумя телами с произведением их масс и обратным квадратом ними расстояния между . В уравнениях поля Эйнштейна он количественно определяет связь между геометрией пространства-времени и тензором энергии-импульса (также называемым тензором энергии-напряжения ).

Измеренное значение константы известно с некоторой достоверностью до четырех значащих цифр. В единицах СИ его значение составляет примерно 6,6743 × 10. ⁻¹¹  N⋅m ² /кг ² .

Современное обозначение закона Ньютона с участием G было введено в 1890-х годах К.В. Бойсом . Первое неявное измерение с точностью около 1% приписывается Генри Кавендишу в эксперименте 1798 года .

Определение

Согласно закону всемирного тяготения Ньютона , величина притяжения силы ( F ) между двумя телами, каждое из которых имеет сферически-симметричное распределение плотности, прямо пропорциональна произведению их m масс 1 _и m 2 _и обратно пропорциональна квадрату расстояние , r направленное вдоль линии, соединяющей их центры масс:

$$F=G{\frac {m_{1}m_{2}}{r^{2}}}.$$

Константа пропорциональности G в этой нерелятивистской формулировке является гравитационной постоянной. В просторечии гравитационную постоянную также называют «Большой G», в отличие от «маленькой g» ( g ), которая представляет собой локальное гравитационное поле Земли (эквивалентное ускорению свободного падения). Где $M_{\oplus }$ это масса Земли и $r_{\oplus }$ — радиус Земли , эти две величины связаны соотношением:

$$g=G{\frac {M_{\oplus }}{r_{\oplus }^{2}}}.$$

Гравитационная постоянная появляется в уравнениях поля Эйнштейна общей теории относительности :

$$G_{\mu \nu }+\Lambda g_{\mu \nu }=\kappa T_{\mu \nu }\,,$$

где G _μν — тензор Эйнштейна (а не гравитационная постоянная, несмотря на использование G ), Λ — космологическая постоянная , g _μν — метрический тензор , T _μν — тензор энергии-импульса , а κ — гравитационная постоянная Эйнштейна , a константа, первоначально введенная Эйнштейном , которая напрямую связана с постоянной Ньютона гравитации:

$$\kappa ={\frac {8\pi G}{c^{4}}}\approx 2.076647(46)\times 10^{-43}\mathrm {\,N^{-1}} .$$

и

Гравитационная постоянная — это физическая константа, которую трудно измерить с высокой точностью. Это связано с тем, что гравитационная сила является чрезвычайно слабой силой по сравнению с другими фундаментальными силами в лабораторном масштабе.

В СИ единицах рекомендуемое CODATA значение гравитационной постоянной составляет:

$G$ = 6.674 30 (15) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻²

Относительная стандартная неопределенность составляет 2,2 × 10. ⁻⁵ .

Натуральные единицы

Из-за ее использования в качестве определяющей константы в некоторых системах естественных единиц , особенно в геометризированных системах единиц , таких как единицы Планка и единицы Стоуни , значение гравитационной постоянной обычно будет иметь числовое значение 1 или значение, близкое к нему, когда выражается в условиях этих единиц. Из-за значительной неопределенности измеренного значения G с точки зрения других известных фундаментальных констант аналогичный уровень неопределенности будет проявляться в значениях многих величин, выраженных в такой системе единиц.

Орбитальная механика

Дополнительная информация: Стандартный гравитационный параметр , орбитальная механика , небесная механика , гравитационная постоянная Гаусса , масса Земли и масса Солнца.

В астрофизике удобно измерять расстояния в парсеках в секунду (км/с) и массы в солнечных единицах M⊙ _{(пк), скорости в километрах} . В этих единицах гравитационная постоянная равна:

$$G\approx 4.3009\times 10^{-3}\ {\mathrm {pc{\cdot }(km/s)^{2}} \,M_{\odot }}^{-1}.$$

В ситуациях, когда приливы важны, соответствующими масштабами длины являются солнечные радиусы , а не парсеки. В этих единицах гравитационная постоянная равна:

$$G\approx 1.90809\times 10^{5}\mathrm {\ (km/s)^{2}} \,R_{\odot }M_{\odot }^{-1}.$$

В орбитальной механике период P объекта на круговой орбите вокруг сферического объекта подчиняется

$$GM={\frac {3\pi V}{P^{2}}},$$

где V — объем внутри радиуса орбиты. Отсюда следует, что

$P^{2}={\frac {3\pi }{G}}{\frac {V}{M}}\approx 10.896\,\mathrm {h^{2}{\cdot }g{\cdot }cm^{-3}\,} {\frac {V}{M}}.$

Этот способ выражения G показывает взаимосвязь между средней плотностью планеты и периодом обращения спутника над ее поверхностью.

Для эллиптических орбит, применяя третий закон Кеплера , выраженный в единицах, характерных для орбиты Земли :

$G=4\pi ^{2}\mathrm {\ AU^{3}{\cdot }yr^{-2}} \ M^{-1}\approx 39.478\mathrm {\ AU^{3}{\cdot }yr^{-2}} \ M_{\odot }^{-1},$

где расстояние измеряется в терминах большой полуоси орбиты Земли ( астрономическая единица , а.е.), времени в годах и массы в общей массе орбитальной системы ( M = M _☉ + M _E + M _☾ ).

Приведенное выше уравнение является точным только в рамках приближения орбиты Земли вокруг Солнца как задачи двух тел в механике Ньютона, измеренные величины содержат поправки от возмущений от других тел Солнечной системы и из общей теории относительности.

Однако с 1964 по 2012 год оно использовалось в качестве определения астрономической единицы и, таким образом, сохранялось по определению:

$$1\ \mathrm {AU} =\left({\frac {GM}{4\pi ^{2}}}\mathrm {yr} ^{2}\right)^{\frac {1}{3}}\approx 1.495979\times 10^{11}\ \mathrm {m} .$$

С 2012 года АС определяется как 1,495 978 707 × 10. ¹¹ m точно, и уравнение уже нельзя считать точным.

Величина GM — произведение гравитационной постоянной и массы данного астрономического тела, такого как Солнце или Земля, — известна как стандартный гравитационный параметр (также обозначаемый μ ). Стандартный гравитационный параметр GM появляется, как указано выше, в законе всемирного тяготения Ньютона, а также в формулах отклонения света, вызванного гравитационным линзированием , в законах движения планет Кеплера и в формуле убегающей скорости .

Эта величина дает удобное упрощение различных формул, связанных с гравитацией. Продукт GM известен гораздо точнее, чем любой другой фактор.

Ценности для GM

Тело	μ = ГМ	Ценить	Относительная неопределенность
Солнце	G M ☉	1.327 124 400 18 (8) × 10 20 м 3 ⋅s −2	6 × 10 −11
Земля	Г М Е	3.986 004 418 (8) × 10 14 м 3 ⋅s −2	2 × 10 −9

Расчеты в небесной механике также можно проводить с использованием единиц солнечной массы , средних солнечных дней и астрономических единиц, а не стандартных единиц СИ. Для этой цели гравитационная постоянная Гаусса исторически широко использовалась k = 0,017 202 098 95 радиан в день , выражающая среднюю угловую скорость системы Солнце-Земля. Использование этой константы и подразумеваемое определение астрономической единицы, обсуждавшееся выше, запрещено МАС с 2012 года.

История измерений

Дополнительная информация: масса Земли , эксперимент Шихаллиона и эксперимент Кавендиша.

Ранняя история

Существование постоянной подразумевается в законе всемирного тяготения Ньютона , опубликованном в 1680-х годах (хотя ее обозначение как G датируется 1890-ми годами). но не рассчитывается в его Philosophiæ Naturalis Principia Mathematica , где постулируется закон обратных квадратов гравитации. В « Началах » Ньютон рассматривал возможность измерения силы тяжести путем измерения отклонения маятника вблизи большого холма, но считал, что эффект будет слишком мал, чтобы его можно было измерить. Тем не менее, у него была возможность оценить порядок величины константы, когда он предположил, что «средняя плотность Земли может быть в пять или шесть раз больше плотности воды», что эквивалентно гравитационной постоянной заказ:

Г ≈ (6,7 ± 0,6) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻²

Измерение было предпринято в 1738 году Пьером Бугером и Шарлем Мари де ла Кондамином в их « Перуанской экспедиции ». Бугер преуменьшил значение своих результатов в 1740 году, предположив, что эксперимент, по крайней мере, доказал, что Земля не может быть полой оболочкой некоторые мыслители того времени, в том числе Эдмонд Галлей . , как предполагали

Эксперимент Шихаллиона , предложенный в 1772 году и завершенный в 1776 году, стал первым успешным измерением средней плотности Земли и, следовательно, косвенно гравитационной постоянной. Результат, сообщенный Чарльзом Хаттоном (1778), предполагал плотность 4,5 г/см. ³ ( в 4 + 1 / 2 раза больше плотности воды), примерно на 20% ниже современного значения. Это немедленно привело к оценкам плотности и массы Солнца , Луны и планет , отправленным Хаттоном Жерому Лаланду для включения в его планетарные таблицы. Как обсуждалось выше, определение средней плотности Земли эквивалентно измерению гравитационной постоянной, учитывая средний радиус Земли и среднее гравитационное ускорение на поверхности Земли, путем установки

$$G=g{\frac {R_{\oplus }^{2}}{M_{\oplus }}}={\frac {3g}{4\pi R_{\oplus }\rho _{\oplus }}}.$$

Исходя из этого, результат Хаттона 1778 года эквивалентен G ≈ 8 × 10. ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² .

Схема крутильных весов, использованных в эксперименте Кавендиша, выполненном Генри Кавендишем в 1798 году, для измерения G с помощью шкива большие шарики, подвешенные на рамке, поворачивались в положение рядом с маленькими шариками.

Первое прямое измерение гравитационного притяжения между двумя телами в лаборатории было выполнено в 1798 году, через семьдесят один год после смерти Ньютона, Генри Кавендишем . Он определил значение G неявно, используя торсионные весы, изобретенные геологом преподобным Джоном Мичеллом (1753 г.). Он использовал горизонтальную торсионную балку со свинцовыми шариками, инерцию которой (по отношению к постоянной кручения) он мог определить, рассчитывая время колебаний балки. Их слабое притяжение к другим шарам, расположенным рядом с балкой, можно было обнаружить по вызванному им отклонению. Несмотря на то, что экспериментальный план был разработан Мичеллом, эксперимент теперь известен как эксперимент Кавендиша из -за его первого успешного проведения Кавендишем.

Заявленной целью Кавендиша было «взвешивание Земли», то есть определение средней плотности Земли и массы Земли . Его результат, ρ _🜨 = 5,448(33) г⋅см. ⁻³ , соответствует значению G = 6,74(4) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² . Это удивительно точное значение, примерно на 1% выше современного значения (сопоставимо с заявленной относительной стандартной неопределенностью 0,6%).

19 век

Точность измеренного значения G увеличилась лишь незначительно со времени первоначального эксперимента Кавендиша. G довольно сложно измерить, поскольку гравитация гораздо слабее других фундаментальных сил, а экспериментальная установка не может быть отделена от гравитационного воздействия других тел.

Измерения маятниками провел Франческо Карлини (1821 г., 4,39 г/см). ³ ), Эдвард Сабин (1827, 4,77 г/см ³ ), Карло Игнацио Джулио (1841, 4,95 г/см ³ ) и Джордж Бидделл Эйри (1854 г., 6,6 г/см). ³ ).

Эксперимент Кавендиша впервые повторил Фердинанд Райх (1838, 1842, 1853), который нашел значение 5,5832(149) г⋅см. ⁻³ , что на самом деле хуже результата Кавендиша, отличаясь от современного значения на 1,5%. Корню и Байль (1873 г.), нашли 5,56 г⋅см. ⁻³ .

Эксперимент Кавендиша оказался более надежным, чем эксперименты с маятником типа «Шихаллион» (отклонение) или «перуанского» типа (период как функция высоты). все еще продолжал проводить эксперименты с маятником Роберт фон Штернек (1883 г., результаты от 5,0 до 6,3 г/см). ³ ) и Томас Корвин Менденхолл (1880, 5,77 г/см). ³ ).

Результат Кавендиша был впервые улучшен Джоном Генри Пойнтингом (1891 г.). опубликовавший значение 5,49(3) г⋅см. ⁻³ , отличающееся от современного значения на 0,2%, но совместимое с современным значением в пределах указанной относительной стандартной неопределенности 0,55%. Помимо Пойнтинга, измерения производил CV Boys (1895 г.). и Карл Браун (1897), с совместимыми результатами, предполагающими G = 6,66(1) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² . Современные обозначения, включающие константу G, были введены Бойсом в 1894 году. и становится стандартом к концу 1890-х годов, при этом значения обычно указываются в системе CGS . Ричарц и Кригар-Мензель (1898) попытались повторить эксперимент Кавендиша, используя 100 000 кг свинца в качестве притягивающей массы. Точность их результата 6,683(11) × 10. ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² Однако он был того же порядка, что и другие результаты того времени.

Артур Стэнли Маккензи в «Законах гравитации» (1899) рассматривает работу, проделанную в 19 веке. Пойнтинг — автор статьи «Гравитация» в Британской энциклопедии одиннадцатом издании (1911 г.). Здесь он приводит значение G = 6,66 × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² с относительной неопределенностью 0,2%.

Современная

Пол Р. Хейл (1930) опубликовал значение 6,670(5) × 10. ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² (относительная неопределенность 0,1%), улучшено до 6,673(3) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² (относительная неопределенность 0,045% = 450 частей на миллион) в 1942 году.

Однако Хейл использовал статистический разброс в качестве своего стандартного отклонения и сам признавал, что измерения с использованием одного и того же материала дали очень похожие результаты, тогда как измерения с использованием разных материалов дали совершенно разные результаты. Следующие 12 лет после своей статьи 1930 года он потратил на более точные измерения, надеясь, что эффект, зависящий от состава, исчезнет, ​​но этого не произошло, как он отметил в своей последней статье 1942 года.

Опубликованные значения G , полученные на основе высокоточных измерений с 1950-х годов, остаются совместимыми с данными Хейла (1930), но в пределах относительной неопределенности около 0,1% (или 1000 частей на миллион) варьируются довольно широко, и не совсем ясно, является ли неопределенность вообще сократился по сравнению с измерениями 1942 года. Некоторые измерения, опубликованные в 1980–2000-х годах, фактически были взаимоисключающими. Поэтому установление стандартного значения G с относительной стандартной неопределенностью лучше 0,1% остается скорее спекулятивным.

К 1969 году значение, рекомендованное Национальным институтом стандартов и технологий (NIST), было указано с относительной стандартной неопределенностью 0,046% (460 частей на миллион), а к 1986 году она была снижена до 0,012% (120 частей на миллион). Но продолжающаяся публикация противоречивых измерений побудило NIST значительно увеличить стандартную неопределенность рекомендованного значения 1998 г. в 12 раз до стандартной неопределенности 0,15%, что больше, чем указанная Хейлом (1930).

Неопределенность была снова снижена в 2002 и 2006 годах, но еще раз повышена на более консервативные 20% в 2010 году, что соответствует относительной стандартной неопределенности 120 частей на миллион, опубликованной в 1986 году. В обновлении 2014 года CODATA снизила неопределенность до 46 частей на миллион, что составляет менее половины значения 2010 года и на один порядок ниже рекомендации 1969 года.

В следующей таблице показаны рекомендуемые значения NIST, опубликованные с 1969 года:

Хронология измерений и рекомендуемые значения G с 1900 года: значения, рекомендованные на основе обзора литературы, показаны красным, отдельные эксперименты на крутильных весах - синим, другие типы экспериментов - зеленым.

Рекомендуемые значения G

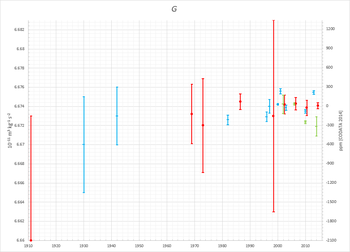
Год	Г (10 −11 м 3 ⋅kg −1 ⋅s −2 )	Относительная стандартная неопределенность	Ссылка.
1969	6.6732(31)	460 частей на миллион
1973	6.6720(49)	730 частей на миллион
1986	6.67449(81)	120 частей на миллион
1998	6.673(10)	1500 частей на миллион
2002	6.6742(10)	150 частей на миллион
2006	6.67428(67)	100 частей на миллион
2010	6.67384(80)	120 частей на миллион
2014	6.67408(31)	46 частей на миллион
2018	6.67430(15)	22 частей на миллион
2022	6.67430(15)	22 частей на миллион

В январском номере журнала Science за 2007 г. Fixler et al. описал измерение гравитационной постоянной с помощью нового метода атомной интерферометрии , сообщив значение G = 6,693(34) × 10. ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² , что на 0,28% (2800 ppm) выше значения CODATA 2006 года. Улучшенное измерение холодных атомов, проведенное Рози и др. было опубликовано в 2014 г. G = 6,671 91 (99) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² . Хотя этот результат намного ближе к принятому значению (что позволяет предположить, что измерения Фикслера и др. были ошибочными), этот результат был на 325 частей на миллион ниже рекомендованного значения CODATA 2014 года с неперекрывающимися стандартными интервалами неопределенности.

По состоянию на 2018 год предпринимаются усилия по переоценке противоречивых результатов измерений, координируемые NIST, в частности, повторение экспериментов, о которых сообщили Куинн и др. (2013).

В августе 2018 года китайская исследовательская группа объявила о новых измерениях, основанных на крутильных весах: 6,674 184 (78) × 10. ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² и 6,674 484 (78) × 10 ⁻¹¹ м ³ ⋅kg ⁻¹ ⋅s ⁻² на основе двух разных методов. Заявлено, что это самые точные измерения, когда-либо проводившиеся, со стандартной погрешностью, составляющей всего 12 частей на миллион. Разница в 2,7 σ между двумя результатами предполагает, что могут быть неучтённые источники ошибок.

Постоянство

Дополнительная информация: Изменение фундаментальных констант во времени.

Анализ наблюдений 580 сверхновых типа Ia показывает, что гравитационная постоянная менялась менее чем на одну десятимиллиардную в год за последние девять миллиардов лет.

См. также

• Гравитация Земли
• Стандартная гравитация
• Гравитационная постоянная Гаусса
• Орбитальная механика
• Скорость убегания
• Гравитационный потенциал
• Гравитационная волна
• Сильная гравитация
• Гипотеза больших чисел Дирака
• Ускоряющееся расширение Вселенной
• Эксперимент по лунной лазерной локации
• Космологическая константа

Ссылки

Сноски

Цитаты

Источники

• Стэндиш., Э. Майлз (1995). «Отчет подгруппы IAU WGAS по числовым стандартам». В Аппенцеллере, И. (ред.). Основные моменты астрономии . Дордрехт: Kluwer Academic Publishers. (Полный отчет доступен онлайн: PostScript ; PDF . Также доступны таблицы из отчета: Астродинамические константы и параметры )
• Гундлах, Йенс Х.; Мерковиц, Стивен М. (2000). «Измерение постоянной Ньютона с помощью крутильных весов с обратной связью по угловому ускорению» . Письма о физических отзывах . 85 (14): 2869–2872. arXiv : gr-qc/0006043 . Бибкод : 2000PhRvL..85.2869G . doi : 10.1103/PhysRevLett.85.2869 . ПМИД   11005956 . S2CID   15206636 .

Внешние ссылки

• Ньютоновская константа гравитации G в Национальном институте стандартов и технологий. Справочники по константам, единицам измерения и неопределенности.
• Споры по поводу гравитационной постоянной Ньютона - дополнительный комментарий к проблемам измерения