Параллелограмм силы
Параллелограмм — это сил метод решения (или визуализации) результатов приложения двух сил к объекту.

Когда задействовано более двух сил, геометрия больше не является параллелограммной, но применяются те же принципы. Силы, являющиеся векторами , подчиняются законам сложения векторов , поэтому общую (результирующую) силу, возникающую в результате приложения ряда сил, можно найти геометрически, нарисовав векторные стрелки для каждой силы. Например, см. рисунок 1. Эта конструкция дает тот же результат, что и перемещение F 2 так, чтобы его хвост совпадал с головкой F 1 , и принятие результирующей силы в качестве вектора, соединяющего хвост F 1 с головкой F 2 . Эту процедуру можно повторить, чтобы добавить F 3 к полученному F 1 + F 2 и так далее. Альтернативно многоугольник сил можно использовать .
Доказательство Ньютона [ править ]

Предварительно: параллелограмм скорости [ править ]
Предположим, что частица движется с постоянной скоростью вдоль линии от А до В (рис. 2) за заданное время (скажем, одну секунду ), в то время как за это же время линия АВ равномерно перемещается из своего положения в АВ в положение в DC, оставаясь параллельным своей первоначальной ориентации повсюду. Учитывая оба движения, частица движется по линии AC. Поскольку смещение в данный момент времени является мерой скорости , длина AB является мерой скорости частицы вдоль AB, длина AD является мерой скорости линии вдоль AD, а длина AC является мерой скорость частицы вдоль AC. Движение частицы такое же, как если бы она двигалась с одной скоростью по AC. [1]
Ньютона параллелограмма Доказательство силы
Предположим, что две силы действуют на частицу в начале координат («хвосты» векторов ) на рисунке 1. Пусть длины векторов F 1 и F 2 представляют скорости, которые две силы могут создать в частице, действуя при заданном время, и пусть направление каждого из них представляет направление, в котором они действуют. Каждая сила действует независимо и будет создавать свою особую скорость независимо от того, действует другая сила или нет. В конце заданного времени частица имеет обе скорости. Согласно приведенному выше доказательству, они эквивалентны одной скорости F net . Согласно второму закону Ньютона , этот вектор также является мерой силы, создающей эту скорость, поэтому две силы эквивалентны одной силе. [2]
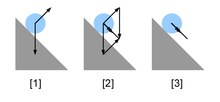
Бернулли для перпендикулярных Доказательство векторов
Мы моделируем силы как евклидовы векторы или члены . Наше первое предположение состоит в том, что равнодействующая двух сил на самом деле является другой силой, так что для любых двух сил есть другая сила .Наше окончательное предположение состоит в том, что равнодействующая двух сил не меняется при вращении. Если — любое вращение (любое ортогональное отображение для обычной структуры векторного пространства с ), то для всех сил
Рассмотрим две перпендикулярные силы длины и длины , с длина .Позволять и , где это вращение между и , так . В условиях инвариантности вращения получаем
Аналогично рассмотрим еще две силы и . Позволять быть вращением от к : , что при осмотре делает .
Применяя эти два уравнения
С и оба лежат рядом , их длины равны
что подразумевает, что имеет длину , что является длиной . Таким образом, для случая, когда и перпендикулярны, . Однако при объединении двух наших наборов вспомогательных сил мы использовали ассоциативность . Используя это дополнительное предположение, ниже мы сформулируем дополнительное доказательство. [3] [4]
силы параллелограмма доказательство Алгебраическое
Мы моделируем силы как евклидовы векторы или члены . Наше первое предположение состоит в том, что равнодействующая двух сил на самом деле является другой силой, так что для любых двух сил есть другая сила . Мы предполагаем коммутативность, поскольку эти силы применяются одновременно, поэтому порядок не имеет значения. .
Рассмотрите карту
Если ассоциативна, то это отображение будет линейным. Поскольку он также отправляет к и к , это также должна быть карта идентификации. Таким образом должен быть эквивалентен обычному оператору сложения векторов. [3] [5]
Споры [ править ]
Математическое доказательство параллелограмма силы не считается математически обоснованным. Были разработаны различные доказательства (главным образом Дючайлы и Пуассона ), которые также вызвали возражения. Не подвергалось сомнению то, что параллелограмм силы верен, но почему он верен. Сегодня параллелограмм силы принимается как эмпирический факт, несводимый к первым принципам Ньютона. [3] [6]
См. также [ править ]
- Ньютона Математические принципы естественной философии , аксиомы или законы движения, следствие I , в Wikisource
- Вектор (геометрический)
- Чистая сила
Ссылки [ править ]
- ^ Раут, Эдвард Джон (1896). Трактат по аналитической статике . Издательство Кембриджского университета. п. 6 . , в книгах Google
- ^ Раут (1896), с. 14
- ^ Jump up to: Перейти обратно: а б с Спивак, Михаил (2010). Механика И. Физика для математиков. Публикуйте или погибните, Inc., стр. 278–282. ISBN 978-0-914098-32-4 .
- ^ Бернулли, Даниэль (1728). Исследование принципов механики и геометрические демонстрации состава и разрешения сил .
- ^ Мах, Эрнест (1974). Наука механика . Open Court Publishing Co., стр. 55–57.
- ^ Ланге, Марк (2009). «Повесть о двух векторах» (PDF) . Диалектика, 63 . стр. 397–431.





































