Глубина удара

Глубина удара снаряда – это расстояние , на которое он проникает в цель, прежде чем остановиться. Физик сэр Исаак Ньютон впервые развил эту идею, чтобы получить грубые приближения к глубине удара снарядов, движущихся с высокими скоростями.

Ньютона для

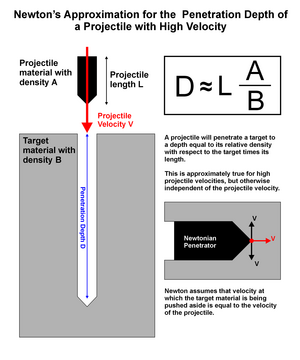
Приближение Ньютона для определения глубины удара снарядов с высокими скоростями основано только на соображениях количества движения . ударника Ничего не сказано ни о том, куда направляется кинетическая энергия , ни о том, что происходит с импульсом после остановки снаряда.

Основная идея проста: ударник несет заданный импульс. Чтобы остановить ударник, этот импульс необходимо передать другой массе. Поскольку скорость ударника настолько высока, что сцеплением внутри целевого материала можно пренебречь, импульс можно передать только материалу (массе) непосредственно перед ударником, который будет толкаться со скоростью ударника. Если ударник с этой скоростью толкнет массу, равную его собственной массе, весь его импульс будет передан массе перед ним, и ударник будет остановлен. В случае цилиндрического ударника к моменту остановки он проникнет на глубину, равную произведению его собственной длины на его относительную плотность по отношению к материалу мишени.

Этот подход справедлив только для узкого диапазона скоростей, меньших скорости звука в материале мишени или ударника.

Если скорость удара превышает скорость звука внутри мишени или материала ударника, ударный удар приводит к разрушению материала, а при более высоких скоростях он ведет себя как газ, вызывая быстрый выброс материала мишени и ударника и образование кратера. . Глубина кратера зависит от свойств материала ударника и мишени, а также скорости удара. Обычно большая скорость удара означает большую глубину кратера.

Приложения

• Снаряд : цельнометаллические снаряды должны быть изготовлены из материала с очень высокой плотностью, например урана (19,1 г/см). ³ ) или свинец (11,3 г/см ³ ). Согласно приближению Ньютона, цельнометаллический снаряд из урана пробьет стальную броню, длина которой примерно в 2,5 раза превышает собственную длину.
• Кумулятивный заряд , базука : Чтобы кумулятивный заряд (противотанковый) мог пробить стальные пластины, важно, чтобы при взрыве образовалась длинная струя тяжелого металла (в кумулятивном заряде, предназначенном для противотанковых целей, при взрыве образуется высокоскоростная струя металла). струя из конусовидной металлической футеровки). Эту струю можно затем рассматривать как ударник в приближении Ньютона.
• Метеорит : Судя по давлению воздуха, состав атмосферы эквивалентен примерно 10 м воды. Поскольку лед имеет примерно такую ​​же плотность, как вода, кубик льда из космоса, летящий со скоростью 15 км/с или около того, должен иметь длину 10 м, чтобы достичь поверхности Земли на высокой скорости. Меньший кубик льда будет замедлен до конечной скорости . Однако более крупный кубик льда также может быть замедлен, если он приближается под очень малым углом и, таким образом, должен пробить большую часть атмосферы. Железный метеорит длиной 1,3 м пробьет атмосферу; меньший будет замедлен воздухом и упадет на землю на предельной скорости.
• Ударный снаряд, разрушитель бункеров : вместо ядерных боеголовок можно использовать твердые ударные элементы для проникновения в бункеры глубоко под землей. По приближению Ньютона урановый снаряд (плотность 19 г/см ³ ) на большой скорости и длине 1 м пробивал бы 6 м породы (плотность 3 г/см2). ³ ) перед остановкой.

См. также

• Сила удара
• Терминальная баллистика

Дальнейшее чтение

• Янг, CW (1967). Разработка эмпирических уравнений для прогнозирования глубины проникновения снаряда в землю (Отчет). Том. СК-ДР-67-60. Альбукерке, Нью-Мексико: Национальные лаборатории Сандии.
• Янг, CW (1997). Уравнения проникновения (PDF) (Отчет). Том. ПЕСОК94-2726. Альбукерке, Нью-Мексико: Национальные лаборатории Сандии. Это отдельный отчет, документирующий последнюю обновленную версию уравнений проникновения Янга/Сандии и связанных с ними аналитических методов прогнозирования проникновения в природные грунты и бетон. См. Приложение A и B для ознакомления с уравнениями проникновения.
• Алексеевский, В.П. (1966). «Проникновение стержня в цель на высокой скорости». Горение, взрыв и ударные волны (Физика Горения и Взрыва) . 2 (2): 99–106. дои : 10.1007/BF00749237 . ISSN   0010-5082 . S2CID   97258659 .
• Тейт, А. (1 ноября 1967 г.). «Теория замедления длинных стержней после удара» (PDF) . Журнал механики и физики твердого тела . 15 (6): 387–399. Бибкод : 1967JMPSo..15..387T . дои : 10.1016/0022-5096(67)90010-5 . Архивировано из оригинала (PDF) 26 марта 2012 года . Проверено 23 июня 2011 г.
• Бернард, Роберт С. (1978). Прогноз глубины и движения проникающих в Землю (отчет). Том. АДА056701. Виксбург, Массачусетс: Экспериментальная станция армейского инженера водных путей Виксбург. Архивировано из оригинала (PDF) 8 октября 2012 года.
• Уолтерс, Уильям П.; Сеглетес, Стивен Б. (1991). «Точное решение уравнений проникновения длинного стержня» . Международный журнал ударной инженерии . 11 (2): 225–231. дои : 10.1016/0734-743X(91)90008-4 .
• Сеглетис, Стивен Б.; Уолтерс, Уильям П. (2002). Эффективное решение уравнений проникновения длинных стержней Алексеевского-Тейта (PDF) (Отчет). Том. АРЛ-ТР-2855. Абердин, Мэриленд: Армейская исследовательская лаборатория Абердинского испытательного полигона, Мэриленд.
• Сеглетес, Стивен Б.; Уолтерс, Уильям П. (2003). «Расширения к точному решению уравнений проникновения/эрозии длинных стержней» (PDF) . Международный журнал ударной инженерии . 28 (4): 363–376. дои : 10.1016/S0734-743X(02)00071-4 . Проверено 23 июня 2011 г.

Внешние ссылки

• Программа воздействия на Землю
• Глубина проникновения космического мусора в зависимости от скорости и диаметра