Причинная структура
В математической физике причинная структура лоренцева многообразия описывает причинные связи между точками в многообразии.
Введение
[ редактировать ]В современной физике (особенно в общей теории относительности ) пространство-время представляется лоренцевым многообразием . Причинно-следственные связи между точками многообразия интерпретируются как описание того, какие события в пространстве-времени могут влиять на какие другие события.
Причинная структура произвольного (возможно, искривленного) лоренцева многообразия усложняется наличием кривизны . Обсуждение причинной структуры таких многообразий должно быть сформулировано в терминах гладких кривых, соединяющих пары точек. Тогда условия на касательных векторах кривых определяют причинно-следственные связи.
Касательные векторы
[ редактировать ]
Если является лоренцевым многообразием (для метрики на коллекторе ) то ненулевые касательные векторы в каждой точке многообразия можно разделить на три непересекающихся типа.Касательный вектор является:
- похоже на время, если
- нулевой или светоподобный , если
- пространственноподобный, если
Здесь мы используем метрическая подпись . Мы говорим, что касательный вектор непространственноподобен, если он равен нулю или времениподобен.
Каноническое лоренцево многообразие — это пространство-время Минковского , где и — плоская метрика Минковского . Названия касательных векторов взяты из физики этой модели. Причинно-следственные связи между точками пространства-времени Минковского принимают особенно простую форму, поскольку касательное пространство также является и, следовательно, касательные векторы можно отождествить с точками пространства. Четырехмерный вектор классифицируется по признаку , где - декартова координата в трехмерном пространстве, - константа, представляющая универсальный предел скорости, а это время. Классификация любого вектора в пространстве будет одинаковой во всех системах отсчета, связанных преобразованием Лоренца (но не общим преобразованием Пуанкаре , поскольку начало координат при этом может быть смещено) из-за инвариантности метрики.
Ориентированность во времени
[ редактировать ]В каждой точке в точки времениподобные касательные векторы в касательном пространстве можно разделить на два класса. Для этого мы сначала определим отношение эквивалентности на парах времениподобных касательных векторов.
Если и являются двумя времениподобными касательными векторами в точке, мы говорим, что и эквивалентны (записаны ) если .
Тогда существуют два класса эквивалентности , которые между собой содержат все времениподобные касательные векторы в точке.Мы можем (произвольно) назвать один из этих классов эквивалентности ориентированным в будущее , а другой — ориентированным в прошлое . Физически такое обозначение двух классов времениподобных векторов, направленных в будущее и прошлое, соответствует выбору стрелки времени в этой точке. Обозначения, ориентированные на будущее и прошлое, могут быть расширены до нулевых векторов в точке за счет непрерывности.
Лоренцево многообразие ориентируемо по времени. [1] если непрерывное обозначение направленных в будущее и направленных в прошлое для непространственноподобных векторов может быть сделано по всему многообразию.
Кривые
[ редактировать ]Путь в представляет собой непрерывную карту где — невырожденный интервал (т. е. связное множество, содержащее более одной точки) в . путь Гладкий имеет дифференцируемы соответствующее количество раз (обычно ), а правильный путь имеет ненулевую производную.
Кривая в — это образ пути или, точнее, класс эквивалентности образов путей, связанных перепараметризацией, т. е. гомеоморфизмами или диффеоморфизмами пути. . Когда является ориентированным по времени, кривая ориентирована, если требуется, чтобы изменение параметра было монотонным .
Сглаживание правильных кривых (или путей) в можно классифицировать в зависимости от их касательных векторов. Такая кривая
- хронологический (или времениподобный ), если касательный вектор времениподобен во всех точках кривой. Также называется мировой линией . [2]
- null , если касательный вектор равен нулю во всех точках кривой.
- пространственноподобен , если касательный вектор пространственноподобен во всех точках кривой.
- причинный (или непространственный ), если касательный вектор времениподобен или равен нулю во всех точках кривой.
Требования регулярности и невырожденности гарантировать, что замкнутые причинные кривые (например, состоящие из одной точки) не допускаются автоматически во все пространства-времени.
Если многообразие ориентировано во времени, то непространственноподобные кривые можно дополнительно классифицировать в зависимости от их ориентации относительно времени.
Хронологическая, нулевая или причинно-следственная кривая является
- направлено в будущее , если для каждой точки кривой касательный вектор направлен в будущее.
- направлено в прошлое , если для каждой точки кривой касательный вектор направлен в прошлое.
Эти определения применимы только к причинным (хронологическим или нулевым) кривым, поскольку только времениподобным или нулевым касательным векторам можно присвоить ориентацию относительно времени.
- Замкнутая времяподобная кривая — это замкнутая кривая, которая везде времениподобна, направленная в будущее (или всюду времениподобна, направленная в прошлое).
- Замкнутая нулевая кривая — это замкнутая кривая, которая везде имеет нулевое значение, направленное в будущее (или всюду нулевое, направленное в прошлое).
- Голономия отношения скорости изменения аффинного параметра вокруг замкнутой нулевой геодезической является фактором красного смещения .
Причинно-следственные связи
[ редактировать ]существует несколько причинно-следственных связей Между точками и в многообразии .
- хронологически предшествует (часто обозначается ), если существует направленная в будущее хронологическая (времяподобная) кривая от к .
- строго причинно предшествует (часто обозначается ), если существует направленная в будущее причинная (непространственноподобная) кривая из к .
- причинно предшествует (часто обозначается или ) если строго причинно предшествует или .
- Горизмос [3] (часто обозначается или ) если или существует направленная в будущее нулевая кривая из к [4] (или, что то же самое, и ).
Эти отношения удовлетворяют следующим свойствам:
- подразумевает (это тривиально следует из определения) [5]
- , подразумевает [5]
- , подразумевает [5]
- , , являются транзитивными . [5] не является транзитивным. [6]
- , являются рефлексивными [4]
Для точки в многообразии мы определяем [5]
- Хронологическое будущее , обозначенный , как множество всех точек в такой, что хронологически предшествует :
- Хронологическое прошлое , обозначенный , как множество всех точек в такой, что хронологически предшествует :
Аналогично определяем
- Причинное будущее (также называемое абсолютным будущим ) , обозначенный , как множество всех точек в такой, что причинно предшествует :
- Причинное прошлое (также называемое абсолютным прошлым ) , обозначенный , как множество всех точек в такой, что причинно предшествует :
- Будущий нулевой конус как совокупность всех точек в такой, что .
- Прошлый нулевой конус как совокупность всех точек в такой, что .
- Световой конус как будущие и прошлые нулевые конусы вместе. [7]
- в другом месте как точки, не находящиеся в световом конусе, причинном будущем или причинном прошлом. [7]
Точки, содержащиеся в , например, можно добраться из по времениподобной кривой, направленной в будущее.Суть можно добраться, например, из точек, содержащихся в направленной в будущее непространственноподобной кривой.
В пространстве-времени Минковского множество — это внутренняя часть будущего светового конуса на . Набор это полный световой конус будущего в , включая сам конус.
Эти наборы определено для всех в в совокупности называются причинной структурой .
Для подмножество мы определяем [5]
Для два подмножества мы определяем
- Хронологическое будущее относительно , , это хронологическое будущее рассматривается как подмногообразие . Обратите внимание, что это совершенно другая концепция что дает набор точек в которого можно достичь с помощью времяподобных кривых, направленных в будущее, начиная с . В первом случае кривые должны лежать в во втором случае нет. См. Хокинг и Эллис.
- Причинное будущее относительно , , является причинным будущим рассматривается как подмногообразие . Обратите внимание, что это совершенно другая концепция что дает набор точек в которого можно достичь с помощью причинно-следственных кривых, направленных в будущее, начиная с . В первом случае кривые должны лежать в во втором случае нет. См. Хокинг и Эллис.
- — Будущее множество это множество, закрытое в хронологическом будущем.
- — Прошлый набор это набор, закрытый по хронологическому прошлому.
- Неразложимое прошлое множество (IP) — это прошлое множество, которое не является объединением двух разных подмножеств открытого прошлого.
- IP, который не совпадает с прошлым какой-либо точки в называется терминальным неразложимым прошлым множеством (TIP).
- Правильный неразложимый набор прошлого (PIP) — это IP, который не является TIP. является собственным неразложимым прошлым множеством (PIP).
- Будущее развитие Коши , это совокупность всех точек для которого каждое прошлое направляло нерастяжимую причинную кривую через пересекает хотя бы один раз. То же самое и с прошлым развитием Коши. Развитие Коши представляет собой объединение будущих и прошлых разработок Коши. Разработки Коши важны для изучения детерминизма .
- Подмножество является хрональным, если не существует такой, что или, что то же самое, если не пересекается с .
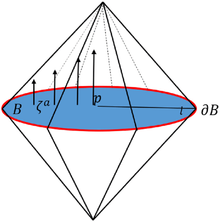
- Поверхность Коши представляет собой замкнутое хрональное множество, развитие Коши которого .
- Метрика называется глобально гиперболической , если она расслаивается на поверхности Коши.
- Множеством , нарушающим хронологию, называется множество точек, через которые проходят замкнутые времениподобные кривые.
- Множество , нарушающее причинность, — это множество точек, через которые проходят замкнутые причинные кривые.
- Границей множества, нарушающего причинность, является горизонт Коши . Если горизонт Коши создается замкнутыми нулевыми геодезическими, то с каждой из них связан коэффициент красного смещения.
- Для причинно-следственной кривой , алмаз причинный (здесь мы используем более широкое определение «кривой», согласно которому это просто набор точек), поскольку точка в причинно-следственном прошлом . Словами: причинный ромб мировой линии частицы. совокупность всех событий, которые лежат как в прошлом, так и в каком-то моменте и будущее какого-то момента в . В дискретной версии причинный ромб представляет собой совокупность всех причинных путей, соединяющих от .
Характеристики
[ редактировать ]См. Пенроуз (1972), стр. 13.
- точка находится в тогда и только тогда, когда находится в .
- Горизм порождается нулевыми геодезическими конгруэнтностями.
Топологические свойства:
- открыт для всех точек в .
- открыт для всех подмножеств .
- для всех подмножеств . Здесь это закрытие подмножества .
Конформная геометрия
[ редактировать ]Две метрики и связаны конформно [8] если для какой-то реальной функции называется конформным фактором . (См. конформную карту ).
Глядя на определения того, какие касательные векторы являются времениподобными, нулевыми и пространственноподобными, мы видим, что они остаются неизменными, если мы используем или . В качестве примера предположим является времениподобным касательным вектором относительно метрика. Это означает, что . Тогда у нас есть это так является времениподобным касательным вектором относительно слишком.
Отсюда следует, что причинная структура лоренцева многообразия не изменяется при конформном преобразовании .
Нулевая геодезическая остается нулевой геодезической при конформном изменении масштаба.
Конформная бесконечность
[ редактировать ]Бесконечная метрика допускает геодезические бесконечной длины/собственного времени. Однако иногда мы можем выполнить конформное масштабирование метрики с конформным коэффициентом, который достаточно быстро падает до 0 по мере приближения к бесконечности, чтобы получить конформную границу многообразия. Топологическая структура конформной границы зависит от причинной структуры.
- Ориентированная в будущее времяподобная геодезическая система в конечном итоге оказывается , будущее время подобно бесконечности .
- Направленная в прошлое времениподобная геодезическая система в конечном итоге оказывается на , прошедшее время подобно бесконечности .
- Ориентированные на будущее нулевые геодезические оказываются на ℐ + , будущая нулевая бесконечность .
- Направленные в прошлое нулевые геодезические оказываются на ℐ − , прошлая нулевая бесконечность .
- Пространственноподобные геодезические оказываются на пространственноподобной бесконечности .
В различных помещениях:
- Пространство Минковского : - точки, ℐ ± являются нулевыми листами, а пространственноподобная бесконечность имеет коразмерность 2.
- Пространство Антиде Ситтера : не существует времениподобной или нулевой бесконечности, а пространственноподобная бесконечность имеет коразмерность 1.
- Пространство де Ситтера : будущее и прошлое времениподобной бесконечности имеют коразмерность 1.
Гравитационная сингулярность
[ редактировать ]Если геодезическая заканчивается после конечного аффинного параметра и невозможно расширить многообразие для расширения геодезической, то мы имеем особенность .
- Для черных дыр заканчивается сингулярностью . будущая времяподобная граница в некоторых местах
- Для Большого взрыва прошедшая времяподобная граница также является сингулярностью.
Абсолютный горизонт событий — это нулевой конус будущего времениподобной бесконечности. Он создается нулевыми геодезическими, которые подчиняются оптическому уравнению Райчаудхури .
См. также
[ редактировать ]- Причинно-динамическая триангуляция (CDT)
- Условия причинности
- Причинные множества
- Поверхность Коши
- Замкнутая времениподобная кривая
- Гипотеза космической цензуры
- Глобально гиперболическое многообразие
- Пространство-время Маламента – Хогарта
- Нулевая бесконечность
- Диаграмма Пенроуза
- Теоремы Пенроуза – Хокинга об особенностях
- Пространство-время
Примечания
[ редактировать ]- ^ Хокинг и Израиль 1979 , с. 255
- ^ Галлоуэй, Грегори Дж. «Заметки о лоренцевой причинности» (PDF) . Летняя школа ESI-EMS-IAMP по математической теории относительности . Университет Майами. п. 4 . Проверено 2 июля 2021 г.
- ^ Пенроуз 1972 , с. 15
- ^ Jump up to: а б Пападопулос, Кириакос; Ачарджи, Сантану; Пападопулос, Бэзил К. (май 2018 г.). «Порядок на световом конусе и его индуцированная топология». Международный журнал геометрических методов в современной физике . 15 (5): 1850069–1851572. arXiv : 1710.05177 . Бибкод : 2018IJGMM..1550069P . дои : 10.1142/S021988781850069X . S2CID 119120311 .
- ^ Jump up to: а б с д и ж Пенроуз 1972 , с. 12
- ^ Стойка, ОК (25 мая 2016 г.). «Причинная структура и измерение пространства-времени на основе горизмотических отношений» . Журнал гравитации . 2016 : 1–6. arXiv : 1504.03265 . дои : 10.1155/2016/6151726 .
- ^ Jump up to: а б Сард 1970 , с. 78
- ^ Хокинг и Эллис 1973 , с. 42
Ссылки
[ редактировать ]- Хокинг, Юго-Запад ; Эллис, GFR (1973), Крупномасштабная структура пространства-времени , Кембридж: Издательство Кембриджского университета, ISBN 0-521-20016-4
- Хокинг, Юго-Запад ; Израиль, В. (1979), Общая теория относительности, обзор столетия Эйнштейна , издательство Кембриджского университета, ISBN 0-521-22285-0
- Пенроуз, Р. (1972), Методы дифференциальной топологии в теории относительности , SIAM, ISBN 0898710057
- Сард, Р.Д. (1970). Релятивистская механика - Специальная теория относительности и классическая динамика частиц . Нью-Йорк: WA Бенджамин. ISBN 978-0805384918 .
Дальнейшее чтение
[ редактировать ]- Г.В. Гиббонс , С.Н. Солодухин; Геометрия малых причинных ромбов arXiv:hep-th/0703098 (Каузальные интервалы)
- С.В. Хокинг , А.Р. Кинг, П.Дж. Маккарти; Новая топология искривленного пространства-времени, включающая причинную, дифференциальную и конформную структуры ; Дж. Математика. Физ. 17 2:174-181 (1976); (Геометрия, Причинная структура )
- А.В. Левичев; Задание конформной геометрии лоренцева многообразия посредством его причинной структуры ; Советская математика. Докл. 35:452-455 (1987); (Геометрия, Причинная структура )
- Д. Маламент ; Класс непрерывных времяподобных кривых определяет топологию пространства-времени ; Дж. Математика. Физ. 18 7:1399-1404 (1977); (Геометрия, Причинная структура )
- А. А. Робб ; Теория времени и пространства ; Издательство Кембриджского университета, 1914 год; (Геометрия, Причинная структура )
- А. А. Робб ; Абсолютные отношения времени и пространства ; Издательство Кембриджского университета, 1921; (Геометрия, Причинная структура )
- А. А. Робб ; Геометрия времени и пространства ; Издательство Кембриджского университета, 1936; (Геометрия, Причинная структура )
- Р.Д. Соркин , Э. Вулгар; Причинный порядок для пространства-времени с лоренцевой метрикой C^0: доказательство компактности пространства причинных кривых ; Классическая и квантовая гравитация 13: 1971–1994 (1996); arXiv:gr-qc/9508018 ( Причинная структура )




















































![{\displaystyle I^{\pm }[S]=\bigcup _{x\in S}I^{\pm }(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ddc5515570ffb796bf518f8c7401a54a83e2d51)
![{\displaystyle J^{\pm }[S]=\bigcup _{x\in S}J^{\pm }(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a46a9fbe4e87ba86f3f19d694596d3324b0a71b)


![{\displaystyle I^{+}[S;T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3eaf5f087095d84a485e274efbca290925578c0)
![{\displaystyle I^{+}[S]\cap T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/351357f6168b362aec1872ed4a58ad07a9861f1f)
![{\displaystyle J^{+}[S;T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52549dda2ad42d2934d0911a7ee94f63aedfdd63)
![{\displaystyle J^{+}[S]\cap T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb6e0e8f575bb27b7ba2540c501c265d1d27caf)





![{\displaystyle I^{+}[S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a477c64fe41db349b644539b8e802f8a49e790d)







![{\displaystyle I^{+}[S]=I^{+}[I^{+}[S]]\subset J^{+}[S]=J^{+}[J^{+}[ С]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/909b7326d282de57ca80e41850a2089418f8def4)
![{\displaystyle I^{-}[S]=I^{-}[I^{-}[S]]\subset J^{-}[S]=J^{-}[J^{-}[ С]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8c07cccba41e8e1bd57d53d501e04a1cfaae561)

![{\displaystyle I^{\pm }[S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d541d82a9b2037fdfcf7512f3d87d4c6e807584)
![{\displaystyle I^{\pm }[S]=I^{\pm }[{\overline {S}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8564f5b519240036fd779620382cca3aabe3e3d1)

![{\displaystyle I^{\pm }[S]\subset {\overline {J^{\pm }[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/314a73f8b144f899285f6db5195002f593103a45)







