Мировая линия

Мировая линия (или мировая линия ) объекта — это путь , который объект следует в 4- мерном пространстве-времени . Это важное понятие современной физики , и особенно теоретической физики .

Понятие «мировой линии» отличается от таких понятий, как « орбита » или « траектория » (например, орбита планеты в космосе или траектория автомобиля на дороге) включением измерения времени и, как правило, охватывает большую область пространства-времени, где траектории, которые воспринимаются прямыми, визуализируются как кривые в пространстве-времени, чтобы показать их ( относительно ) более абсолютные состояния положения — чтобы раскрыть природу специальной теории относительности или гравитационных взаимодействий.

Идея мировых линий была выдвинута физиками и впервые была предложена Германом Минковским . Этот термин сейчас чаще всего используется в контексте теорий относительности (т. е. специальной теории относительности и общей теории относительности ).

Использование в физике [ править ]

Мировая линия объекта (обычно аппроксимируемая точкой в пространстве, например, частицей или наблюдателем) представляет собой последовательность пространственно-временных событий, соответствующую истории объекта. Мировая линия — это особый тип кривой в пространстве-времени. Ниже будет объяснено эквивалентное определение: Мировая линия — это либо времяподобная, либо нулевая кривая в пространстве-времени. Каждая точка мировой линии — это событие, которое можно пометить временем и пространственным положением объекта в этот момент.

Например, орбита Земли в космосе представляет собой примерно круг, трёхмерную (замкнутую) кривую в космосе: Земля каждый год возвращается в одну и ту же точку пространства относительно Солнца. Однако он прибывает туда в другое (более позднее) время. Таким образом, мировая линия Земли является спиральной в пространстве-времени (кривая в четырехмерном пространстве) и не возвращается в одну и ту же точку.

Пространство-время — это совокупность событий вместе с непрерывной и плавной системой координат, идентифицирующей эти события. Каждое событие можно обозначить четырьмя числами: временной координатой и тремя пространственными координатами; таким образом, пространство-время является четырехмерным пространством. Математический термин для пространства-времени — это четырехмерное многообразие (топологическое пространство, локально напоминающее евклидово пространство вблизи каждой точки). Эту концепцию можно применить и к многомерному пространству. Для упрощения четырехмерной визуализации две пространственные координаты часто скрываются. Затем событие представляется точкой на диаграмме Минковского , которая представляет собой плоскость, обычно отображаемую с временной координатой, скажем $t$ , по вертикали, и пространственная координата, скажем $x$ , горизонтально. Как выразился Ф. Р. Харви

Кривая М в [пространстве-времени] называется мировой линией частицы , если ее касательная в каждой точке является будущим времениподобным. Параметр длины дуги называется собственным временем и обычно обозначается τ. Длина М называется собственным временем частицы. Если мировая линия M является отрезком, то говорят, что частица находится в свободном падении . ^[1]^: 62–63

Мировая линия прослеживает путь одной точки в пространстве-времени. Мировой лист — это аналогичная двумерная поверхность, очерченная одномерной линией (например, струной), проходящей через пространство-время. Мировой лист открытой струны (со свободными концами) представляет собой полосу; замкнутая струна (петля) напоминает трубку.

Когда объект аппроксимируется не просто как точка, а имеет расширенный объем, он описывает не мировую линию , а скорее мировую трубу.

Мировые линии как способ описания событий [ править ]

Мировая линия, мировой лист и мировой объем, поскольку они произошли от частиц , струн и бран .

Одномерную линию или кривую можно представить координатами как функцию одного параметра. Каждое значение параметра соответствует точке пространства-времени, а изменение параметра вычерчивает линию. Таким образом, в математических терминах кривая определяется четырьмя координатными функциями. $x^{a}(\tau ),\;a=0,1,2,3$ (где $x^{0}$ обычно обозначает координату времени) в зависимости от одного параметра $\tau$ . Координатная сетка в пространстве-времени — это набор кривых, который получается, если три из четырех координатных функций присвоить константам.

Иногда термин «мировая линия» неофициально используется для обозначения любой кривой в пространстве-времени. Эта терминология вызывает путаницу. Точнее, мировая линия — это кривая в пространстве-времени, которая отслеживает (временную) историю частицы, наблюдателя или небольшого объекта. В качестве параметра кривой обычно используют собственное время объекта или наблюдателя. $\tau$ по мировой линии.

кривых пространства- времени Тривиальные примеры

Три разные мировые линии, представляющие движение с разными постоянными четырехскоростными скоростями. t — время и *x .* расстояние

Кривая, состоящая из сегмента горизонтальной линии (линии в постоянном координатном времени), может представлять собой стержень в пространстве-времени и не будет мировой линией в собственном смысле. Параметр просто отслеживает длину стержня.

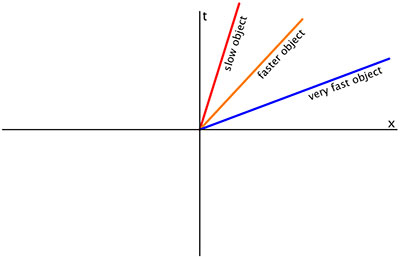
Линия с постоянной пространственной координатой (вертикальная линия в соответствии с принятым выше соглашением) может представлять покоящуюся частицу (или неподвижного наблюдателя). Наклонная линия представляет частицу с постоянной координатной скоростью (постоянное изменение пространственной координаты с увеличением временной координаты). Чем больше линия наклонена от вертикали, тем больше скорость.

Две мировые линии, которые начинаются отдельно, а затем пересекаются, означают столкновение или «встречу». Две мировые линии, начинающиеся в одном и том же событии в пространстве-времени, каждая из которых впоследствии следует своим собственным путем, могут представлять, например, распад одной частицы на две другие или испускание одной частицы другой.

Мировые линии частицы и наблюдателя могут быть связаны между собой с мировой линией фотона (путем света) и образовывать диаграмму, изображающую испускание фотона частицей, которую впоследствии наблюдает наблюдатель (или поглощает другая частица). ).

линии: четырехскоростной вектор Касательный к мировой

Четыре координатные функции $x^{a}(\tau ),\;a=0,1,2,3$ определяющие мировую линию, являются действительными числовыми функциями действительной переменной. $\tau$ и их можно просто дифференцировать с помощью обычного исчисления. Без существования метрики (это важно осознавать) можно представить разницу между точкой $p$ на кривой при значении параметра $\tau _{0}$ и точку на кривой немного (параметр $\tau _{0}+\Delta \tau$ ) дальше. В пределе $\Delta \tau \to 0$ , эта разница делится на $\Delta \tau$ определяет вектор, касательный вектор мировой линии в точке $p$ . Это четырехмерный вектор, определенный в точке $p$ . Она связана с нормальной трехмерной скоростью объекта (но это не одно и то же) и поэтому называется четырехскоростной. ${\vec {v}}$ , или в компонентах:

{\vec {v}}=\left(v^{0},v^{1},v^{2},v^{3}\right)=\left({\frac {dx^{0}}{d\tau }}\;,{\frac {dx^{1}}{d\tau }}\;,{\frac {dx^{2}}{d\tau }}\;,{\frac {dx^{3}}{d\tau }}\right)

такие, что производные берутся в точке $p$ , так что в $\tau =\tau _{0}$ .

Все кривые, проходящие через точку p, имеют касательный вектор, а не только мировые линии. Сумма двух векторов снова является касательным вектором к какой-либо другой кривой, и то же самое справедливо и для умножения на скаляр. Следовательно, все касательные векторы для точки p охватывают линейное пространство , называемое касательным пространством в точке p. Например, если взять двумерное пространство, такое как (искривленная) поверхность Земли, ее касательное пространство в определенной точке будет плоской аппроксимацией искривленного пространства.

Мировые линии в специальной теории относительности [ править ]

До сих пор мировая линия (и концепция касательных векторов) описывалась без средств количественного определения интервала между событиями. Базовая математика такова: специальная теория относительности накладывает некоторые ограничения на возможные мировые линии. В специальной теории относительности описание пространства-времени ограничено специальными системами координат, которые не ускоряются (и, следовательно, не вращаются), называемыми инерциальными системами координат . В таких системах координат скорость света является постоянной. Структура пространства-времени определяется билинейной формой η, которая дает вещественное число для каждой пары событий. Билинейную форму иногда называют метрикой пространства-времени , но поскольку отдельные события иногда приводят к нулевому значению, в отличие от метрик в метрических пространствах математики, билинейная форма не является математической метрикой пространства-времени.

Мировые линии свободно падающих частиц/объектов называются геодезическими . В специальной теории относительности это прямые линии в пространстве Минковского .

Часто единицы времени выбираются так, что скорость света изображается линиями под фиксированным углом, обычно под углом 45 градусов, образующими конус с вертикальной (временной) осью. В общем, полезные кривые в пространстве-времени могут быть трёх типов (остальные типы будут частично одного, частично другого типа):

светоподобные кривые, имеющие в каждой точке скорость света. Они образуют конус в пространстве-времени, разделяя его на две части. Конус является трехмерным в пространстве-времени, выглядит как линия на чертежах с подавленными двумя измерениями и как конус на чертежах с подавленным одним пространственным измерением.

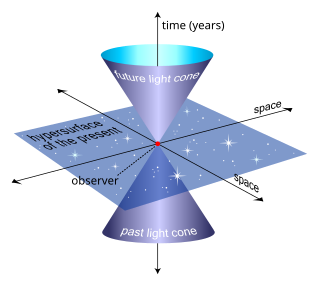
Мгновенно движущиеся вместе инерциальные системы координат по траектории («мировой линии») быстро ускоряющегося наблюдателя (центра). Вертикальное направление указывает время, горизонтальное — расстояние, пунктирная линия — пространство-время наблюдателя. Маленькие точки — это конкретные события в пространстве-времени. Обратите внимание, как в данный момент движущаяся вместе с ним инерциальная система отсчета меняется, когда наблюдатель ускоряется.

времяподобные кривые, со скоростью меньшей скорости света. Эти кривые должны попадать в конус, определяемый светоподобными кривыми. В нашем определении выше: мировые линии — это временные кривые в пространстве-времени .
пространственные кривые, выходящие за пределы светового конуса. Такие кривые могут описывать, например, длину физического объекта. Окружность цилиндра и длина стержня представляют собой пространственноподобные кривые.

При данном событии на мировой линии пространство-время ( пространство Минковского ) делится на три части.

Будущее . данного события формируется всеми событиями, до которых можно добраться через времяподобные кривые, лежащие внутри светового конуса будущего
Прошлое с данного события формируется всеми событиями, которые могут повлиять на событие (то есть могут быть связаны мировыми линиями внутри светового конуса прошлого данным событием).
- Световой конус при данном событии формируется всеми событиями, которые можно связать посредством световых лучей с событием. Когда мы наблюдаем небо ночью, мы в основном видим только прошлый световой конус во всем пространстве-времени.
В другом месте находится область между двумя световыми конусами. наблюдателя Точки в другом месте ему недоступны; только точки в прошлом могут посылать сигналы наблюдателю. В обычном лабораторном опыте с использованием обычных единиц и методов измерения может показаться, что мы смотрим в настоящее, но на самом деле всегда существует время задержки распространения света. Например, мы видим Солнце таким, каким оно было около 8 минут назад, а не таким, какое оно «прямо сейчас». В отличие от настоящего в теории Галилея/Ньютона, в остальном оно толстое; это не трехмерный объем, а четырехмерная область пространства-времени.
- В «где-то еще» включена одновременная гиперплоскость , которая определяется для данного наблюдателя пространством , гиперболически ортогональным его мировой линии. На самом деле он трехмерен, хотя на диаграмме это будет двухплоскость, потому что нам пришлось отбросить одно измерение, чтобы создать понятную картину. Хотя световые конусы одинаковы для всех наблюдателей в данном пространственно-временном событии, у разных наблюдателей с разными скоростями, но совпадающими в событии (точке) пространства-времени, мировые линии пересекаются под углом, определяемым их относительными скоростями. и, таким образом, они имеют разные одновременные гиперплоскости.
- Настоящее часто означает одно рассматриваемое пространственно-временное событие.

Одновременная гиперплоскость [ править ]

Поскольку мировая линия $w(\tau )\in R^{4}$ определяет 4-вектор скорости $v={\frac {dw}{d\tau }}$ это времяподобно, форма Минковского $\eta (v,x)$ определяет линейную функцию $R^{4}\rightarrow R$ к $x\mapsto \eta (v,x).$ Пусть N — нулевое пространство этого линейного функционала. Тогда N называется одновременной гиперплоскостью относительно v . Относительность одновременности — это утверждение, что N зависит от v . Действительно, N — ортогональное дополнение к v относительно η. Когда две мировые линии u и w связаны соотношением ${\frac {du}{d\tau }}={\frac {dw}{d\tau }},$ тогда они разделяют одну и ту же одновременную гиперплоскость. Эта гиперплоскость существует математически, но физические отношения в теории относительности предполагают движение информации посредством света. Например, традиционная электростатическая сила, описываемая законом Кулона, может быть изображена в одновременной гиперплоскости, но релятивистские отношения заряда и силы включают запаздывающие потенциалы .

Мировые линии в общей теории относительности [ править ]

Использование мировых линий в общей теории относительности в основном такое же, как и в специальной теории относительности , с той разницей, что пространство-время может быть искривлено . Метрика существует , и ее динамика определяется уравнениями поля Эйнштейна и зависит от распределения массы-энергии в пространстве-времени. Опять же, метрика определяет светоподобные (нулевые), пространственноподобные и времениподобные кривые. Кроме того, в общей теории относительности мировые линии включают времяподобные кривые и нулевые кривые в пространстве-времени, где времениподобные кривые попадают в световой конус. Однако световой конус не обязательно наклонен под углом 45 градусов к оси времени. Однако это артефакт выбранной системы координат и отражает координатную свободу ( инвариантность диффеоморфизма ) общей теории относительности. Любая времяподобная кривая допускает сопутствующего наблюдателя , чья «ось времени» соответствует этой кривой, и, поскольку ни один наблюдатель не имеет привилегий, мы всегда можем найти локальную систему координат, в которой световые конусы наклонены под углом 45 градусов к оси времени. См. также, например, координаты Эддингтона-Финкельштейна. .

Мировые линии свободно падающих частиц или объектов (например, планет вокруг Солнца или космонавта в космосе) называются геодезическими .

Мировые линии в квантовой теории поля [ править ]

Квантовая теория поля, основа, в которой описывается вся современная физика элементарных частиц, обычно описывается как теория квантованных полей. Однако, хотя это и не получило широкого признания, оно было известно со времен Фейнмана. ^[2]что многие квантовые теории поля могут быть эквивалентным образом описаны в терминах мировых линий. Это предшествовало большей части его работы. ^[3]по формулировке, которая впоследствии стала более стандартной. Формулировка мировой линии квантовой теории поля оказалась особенно плодотворной для различных расчетов в калибровочных теориях. ^[4]^[5]^[6] и при описании нелинейных эффектов электромагнитных полей. ^[7]^[8]

Мировые линии в литературе [ править ]

В 1884 году Ч. Хинтон написал эссе «Что такое четвертое измерение?», которое опубликовал как научный роман . Он написал

Почему же тогда четырехмерные существа не должны быть нами и нашими последовательными состояниями, прохождением их через трехмерное пространство, которым ограничено наше сознание? ^[9]^: 18–19

Популярное описание мировых линий человечества было дано Дж. К. Филдсом из Университета Торонто на заре теории относительности. Как описал адвокат из Торонто Норман Робертсон:

Я помню, как [Филдс] читал лекцию на одной из субботних вечерних лекций в Королевском канадском институте . Ее рекламировали как «математическую фантазию» — и так оно и было! Суть упражнения заключалась в следующем: он постулировал, что, начиная с момента своего рождения, каждое человеческое существо имело некую духовную ауру с прикрепленной к нему длинной нитью или нитью, которая путешествовала за ним на протяжении всей его жизни. Затем он начал в воображении описывать сложную запутанность, в которую каждый человек вовлечен в свои отношения с другими людьми, сравнивая простые запутанности юности с теми сложными узлами, которые возникают в более поздней жизни. ^[10]

Курт Воннегут в своем романе «Бойня номер пять» описывает мировые линии звезд и людей:

«Билли Пилигрим говорит, что Вселенная не выглядит для существ с Тральфамадора множеством ярких маленьких точек. Существа могут видеть, где была каждая звезда и куда она движется, так что небеса наполнены редкими светящимися спагетти. И тральфамадорцы также не считают людей двуногими существами. Они видят в них огромные многоножки — «с ногами младенцев на одном конце и ногами стариков на другом», — говорит Билли Пилигрим.

Почти все научно-фантастические рассказы, которые активно используют эту концепцию, например, для путешествий во времени , чрезмерно упрощают эту концепцию до одномерной временной шкалы, чтобы она соответствовала линейной структуре, которая не соответствует моделям реальности. Такие машины времени часто изображаются мгновенными, их содержимое уходит в одно время и прибывает в другое, но в одной и той же буквально географической точке пространства. Это часто выполняется без указания системы отсчета или с неявным предположением, что система отсчета является локальной; как таковое, для этого потребуется либо точная телепортация, поскольку вращающаяся планета, находящаяся под ускорением, не является инерциальной системой отсчета, либо машина времени останется в том же месте, а ее содержимое «заморожено».

Автор Оливер Франклин опубликовал научно-фантастическую в 2008 году работу под названием «Мировые линии» , в которой изложил упрощенное объяснение гипотезы для непрофессионалов. ^[11]

В рассказе «Линия жизни» автор Роберт А. Хайнлайн описывает мировую линию человека: ^[12]

Он подошел к одному из репортеров. «Предположим, мы возьмем вас в качестве примера. Вас зовут Роджерс, не так ли? Очень хорошо, Роджерс, вы — пространственно-временное событие, имеющее продолжительность в четырех направлениях. Ваш рост не совсем шесть футов, ширина около двадцати дюймов, а ширина — около двадцати дюймов. во времени позади вас простирается еще больше этого пространственно-временного события, достигающего, возможно, девятнадцати шестнадцати лет, поперечное сечение которого мы видим здесь под прямым углом к оси времени и такое же толстое, как настоящее. В дальнем конце — младенец, пахнущий кислым молоком и пускающий слюни на нагрудник. На другом конце лежит, наверное, старик где-то из восьмидесятых.

«Представьте себе это пространственно-временное событие, которое мы называем Роджерсом, в виде длинного розового червя, продолжающегося годами, один конец в утробе матери, а другой в могиле...»

в книге Хайнлайна « Дети Мафусаила» Этот термин используется Джеймса Блиша , как и в книге «Квинконкс времени» (расширенная версия слова «Beep»).

Визуальный роман под названием Steins;Gate , созданный 5pb. , рассказывает историю, основанную на смещении мировых линий. Steins;Gate — часть серии « Научные приключения ». Мировые линии и другие физические концепции, такие как море Дирака, также используются на протяжении всего сериала.

Нила Стивенсона Роман «Анафем» представляет собой долгое обсуждение мировых линий за ужином в разгар философских дебатов между платоническим реализмом и номинализмом .

«Абсолютный выбор» изображает различные мировые линии как второстепенный сюжет и механизм настройки.

Космическая армада, пытающаяся пройти (почти) замкнутый времяподобный путь в качестве стратегического маневра, образует фон и основной сюжетный прием «Неба сингулярности» Чарльза Стросса .

См. также [ править ]

Конкретные типы мировых линий
- Геодезика
- Замкнутые времяподобные кривые
- Причинная структура , кривые, которые представляют множество различных типов мировых линий.
- Изотропная линия
Диаграмма Фейнмана
География времени

Ссылки [ править ]

^ Харви, Ф. Риз (1990). Раздел «Специальная теория относительности» главы «Евклидово/лоренцево векторное пространство» . Спиноры и калибровки . Академическая пресса . стр. 62–67. ISBN 9780080918631 .
^ Фейнман, Ричард П. (1950). «Математическая формулировка квантовой теории электромагнитного взаимодействия» . Физический обзор . 80 (1): 108–128. дои : 10.1103/PhysRev.80.440 .
^ Фейнман, Ричард П. (1951). «Операторное исчисление, имеющее приложения в квантовой электродинамике» (PDF) . Физический обзор . 84 (3): 440–457. Бибкод : 1951PhRv...84..108F . дои : 10.1103/PhysRev.84.108 .
^ Берн, Цви ; Косовер, Дэвид А. (1991). «Эффективный расчет амплитуд однопетлевой КХД». Письма о физических отзывах . 66 (13): 1669–1672. Бибкод : 1991PhRvL..66.1669B . дои : 10.1103/PhysRevLett.66.1669 . ПМИД 10043277 .
^ Берн, Цви ; Диксон, Лэнс ; Косауэр, Дэвид А. (1996). «Прогресс в однопетлевых вычислениях КХД» (PDF) . Ежегодный обзор ядерной науки и науки о элементарных частицах . 46 : 109–148. arXiv : hep-ph/9602280 . Бибкод : 1996ARNPS..46..109B . дои : 10.1146/annurev.nucl.46.1.109 .
^ Шуберт, Кристиан (2001). «Пертурбативная квантовая теория поля в струнном формализме». Отчеты по физике . 355 (2–3): 73–234. arXiv : hep-th/0101036 . Бибкод : 2001ФР...355...73С . дои : 10.1016/S0370-1573(01)00013-8 . S2CID 118891361 .
^ Аффлек, Ян К .; Альварес, Орландо; Мэнтон, Николас С. (1982). «Рождение пар при сильной связи в слабых внешних полях». Ядерная физика Б . 197 (3): 509–519. Бибкод : 1982НуФБ.197..509А . дои : 10.1016/0550-3213(82)90455-2 .
^ Данн, Джеральд В.; Шуберт, Кристиан (2005). «Мировая линия инстантонов и рождение пар в неоднородных полях» (PDF) . Физический обзор D . 72 (10): 105004. arXiv : hep-th/0507174 . Бибкод : 2005PhRvD..72j5004D . дои : 10.1103/PhysRevD.72.105004 . S2CID 119357180 .
^ Хинтон, Швейцария (1884 г.). «Что такое четвертое измерение?» . Научные романы: Первая серия . С. Зонненшайн . стр. 1–32.
^ Робинсон, Жильбер де Борегар (1979). Математический факультет Университета Торонто, 1827–1978 гг . Университет Торонто Пресс . п. 19. ISBN 0-7727-1600-5 .
^ Оливер Франклин (2008). Мировые линии . Эпическая пресса. ISBN 978-1-906557-00-3 .
^ «Техновелия: Хроновитаметр» . Проверено 8 сентября 2010 г.

Минковский, Герман (1909), «Пространство и время» , Physical Journal , 10 : 75–88.

Различные английские переводы на Wikisource: Пространство и время

Людвик Зильберштейн (1914) Теория относительности , стр. 130, Macmillan and Company .

Внешние ссылки [ править ]

Статья о мировых линиях на h2g2 .

подробный текст о мировых линиях и специальной теории относительности

[1] Харви, Ф. Риз (1990). Раздел «Специальная теория относительности» главы «Евклидово/лоренцево векторное пространство» . Спиноры и калибровки . Академическая пресса . стр. 62–67. ISBN 9780080918631 .

[2] Фейнман, Ричард П. (1950). «Математическая формулировка квантовой теории электромагнитного взаимодействия» . Физический обзор . 80 (1): 108–128. дои : 10.1103/PhysRev.80.440 .

[3] Фейнман, Ричард П. (1951). «Операторное исчисление, имеющее приложения в квантовой электродинамике» (PDF) . Физический обзор . 84 (3): 440–457. Бибкод : 1951PhRv...84..108F . дои : 10.1103/PhysRev.84.108 .

[4] Берн, Цви ; Косовер, Дэвид А. (1991). «Эффективный расчет амплитуд однопетлевой КХД». Письма о физических отзывах . 66 (13): 1669–1672. Бибкод : 1991PhRvL..66.1669B . дои : 10.1103/PhysRevLett.66.1669 . ПМИД 10043277 .

[5] Берн, Цви ; Диксон, Лэнс ; Косауэр, Дэвид А. (1996). «Прогресс в однопетлевых вычислениях КХД» (PDF) . Ежегодный обзор ядерной науки и науки о элементарных частицах . 46 : 109–148. arXiv : hep-ph/9602280 . Бибкод : 1996ARNPS..46..109B . дои : 10.1146/annurev.nucl.46.1.109 .

[6] Шуберт, Кристиан (2001). «Пертурбативная квантовая теория поля в струнном формализме». Отчеты по физике . 355 (2–3): 73–234. arXiv : hep-th/0101036 . Бибкод : 2001ФР...355...73С . дои : 10.1016/S0370-1573(01)00013-8 . S2CID 118891361 .

[7] Аффлек, Ян К .; Альварес, Орландо; Мэнтон, Николас С. (1982). «Рождение пар при сильной связи в слабых внешних полях». Ядерная физика Б . 197 (3): 509–519. Бибкод : 1982НуФБ.197..509А . дои : 10.1016/0550-3213(82)90455-2 .

[8] Данн, Джеральд В.; Шуберт, Кристиан (2005). «Мировая линия инстантонов и рождение пар в неоднородных полях» (PDF) . Физический обзор D . 72 (10): 105004. arXiv : hep-th/0507174 . Бибкод : 2005PhRvD..72j5004D . дои : 10.1103/PhysRevD.72.105004 . S2CID 119357180 .

[9] Хинтон, Швейцария (1884 г.). «Что такое четвертое измерение?» . Научные романы: Первая серия . С. Зонненшайн . стр. 1–32.

[10] Робинсон, Жильбер де Борегар (1979). Математический факультет Университета Торонто, 1827–1978 гг . Университет Торонто Пресс . п. 19. ISBN 0-7727-1600-5 .

[Franklin-11] Оливер Франклин (2008). Мировые линии . Эпическая пресса. ISBN 978-1-906557-00-3 .

[12] «Техновелия: Хроновитаметр» . Проверено 8 сентября 2010 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]