Поток

Поток описывает любой эффект, который кажется проходящим или путешествующим (независимо от того, движется он на самом деле или нет) через поверхность или вещество. Поток — это концепция прикладной математики и векторного исчисления , имеющая множество приложений в физике . Для явлений переноса поток представляет собой векторную величину, описывающую величину и направление потока вещества или свойства. В векторном исчислении поток — это скалярная величина, определяемая как поверхностный интеграл от перпендикулярной компоненты векторного поля по поверхности. ^[1]

Терминология [ править ]

Слово флюс происходит от латинского слова : fluxus означает «течь», а fluere — «течь». ^[2] Как флюксия , этот термин был введен в дифференциальное исчисление Исааком Ньютоном .

Концепция теплового потока была ключевым вкладом Жозефа Фурье в анализ явлений теплопередачи. ^[3] Его основополагающий трактат теплоты «Аналитическая теория » ^[4] определяет текучесть как центральную величину и приступает к выводу теперь хорошо известных выражений потока через разницу температур поперек плиты, а затем, в более общем плане, через температурные градиенты или перепады температур в других геометриях. Можно утверждать, основываясь на работе Джеймса Клерка Максвелла : ^[5] что определение переноса предшествует определению потока, используемому в электромагнетизме . Конкретная цитата Максвелла:

В случае потоков мы должны взять интеграл по поверхности от потока, проходящего через каждый элемент поверхности. Результат этой операции называется поверхностным интегралом потока. Он представляет собой количество, которое проходит через поверхность.
— Джеймс Клерк Максвелл

Согласно определению транспорта, поток может быть одним вектором или векторным полем/функцией положения. В последнем случае поток легко интегрируется по поверхности. Напротив, согласно определению электромагнетизма, поток представляет собой интеграл по поверхности; нет смысла интегрировать поток второго определения, поскольку интегрирование будет происходить дважды по поверхности. Таким образом, цитата Максвелла имеет смысл только в том случае, если «поток» используется в соответствии с определением переноса (и, кроме того, это векторное поле, а не одиночный вектор). Это иронично, поскольку Максвелл был одним из главных разработчиков того, что мы сейчас называем «электрическим потоком» и «магнитным потоком» в соответствии с определением электромагнетизма. Их имена в соответствии с цитатой (и определением переноса) будут «поверхностный интеграл электрического потока» и «поверхностный интеграл магнитного потока», и в этом случае «электрический поток» вместо этого будет определяться как «электрическое поле» и «магнитный поток». определяется как «магнитное поле». Это означает, что Максвелл рассматривал эти поля как своего рода потоки/потоки.

Учитывая поток согласно определению электромагнетизма, соответствующая плотность потока , если этот термин используется, относится к его производной вдоль интегрированной поверхности. По Основной теореме исчисления соответствующая плотность потока является потоком согласно определению переноса. Учитывая такой ток , как электрический ток — заряд за время, плотность тока также будет потоком в соответствии с определением переноса — заряд за время на площадь. Из-за противоречивых определений потока и взаимозаменяемости потоков , потока и тока в нетехническом английском языке все термины, используемые в этом параграфе, иногда используются взаимозаменяемо и неоднозначно. Конкретные флюсы в оставшейся части этой статьи будут использоваться в соответствии с их широким признанием в литературе, независимо от того, какому определению флюса соответствует этот термин.

Поток как скорость потока на единицу площади [ править ]

В явлениях переноса ( теплообмен , массоперенос и гидродинамика ) поток определяется как скорость потока объекта на единицу площади, имеющая размеры [количество]·[время] ⁻¹·[область] ⁻¹. ^[6] Площадь представляет собой поверхность, «сквозь» или «поперек» которой протекает объект недвижимости. Например, количество воды, протекающей через поперечное сечение реки каждую секунду, разделенное на площадь этого поперечного сечения, или количество солнечной энергии, попадающей на участок земли каждую секунду, разделенное на площадь этого участка: являются разновидностью флюса.

Общее математическое определение (транспорт) [ править ]

Вот 3 определения в порядке возрастания сложности. Каждый из них является частным случаем следующего. Во всех случаях часто встречающийся символ j (или J ) используется для обозначения потока, q для физической величины текущей , t для времени и A для площади. Эти идентификаторы будут выделены жирным шрифтом тогда и только тогда, когда они являются векторами.

Во-первых, поток как (одиночный) скаляр:

j={\frac {I}{A}},

где

I=\lim _{\Delta t\to 0}{\frac {\Delta q}{\Delta t}}={\frac {\mathrm {d} q}{\mathrm {d} t}}.

В этом случае поверхность, на которой измеряется поток, фиксирована и имеет A. площадь Поверхность предполагается плоской, а течение везде постоянным относительно положения и перпендикулярным поверхности.

Во-вторых, поток как скалярное поле, определенное вдоль поверхности, т.е. функция точек на поверхности:

j(\mathbf {p} )={\frac {\partial I}{\partial A}}(\mathbf {p} ),

I(A,\mathbf {p} )={\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ).

Как и ранее, поверхность предполагается плоской, а течение всюду перпендикулярным ей. Однако поток не обязательно должен быть постоянным. q теперь является функцией p , точки на поверхности, и A , площади. Вместо того, чтобы измерять общий поток через поверхность, q измеряет поток через диск с областью A с центром в точке p вдоль поверхности.

Наконец, поток как векторное поле :

\mathbf {j} (\mathbf {p} )={\frac {\partial \mathbf {I} }{\partial A}}(\mathbf {p} ),

\mathbf {I} (A,\mathbf {p} )={\underset {\mathbf {\hat {n}} }{\operatorname {arg\,max} }}\mathbf {\hat {n}} _{\mathbf {p} }{\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ,\mathbf {\hat {n}} ).

В этом случае нет фиксированной поверхности, над которой мы измеряем. q - функция точки, площади и направления (задаваемая единичным вектором

\mathbf {\hat {n}}

) и измеряет поток через диск площади A, перпендикулярный этому единичному вектору. I определяется выбором единичного вектора, который максимизирует поток вокруг точки, поскольку истинный поток максимизируется на диске, перпендикулярном ему. Таким образом, единичный вектор однозначно максимизирует функцию, когда он указывает на «истинное направление» потока. (Строго говоря, это злоупотребление обозначениями , поскольку «arg max» не может напрямую сравнивать векторы; вместо этого мы берем вектор с наибольшей нормой.)

Свойства [ править ]

Эти прямые определения, особенно последнее, довольно громоздки. Например, конструкция arg max является искусственной с точки зрения эмпирических измерений, когда с помощью флюгера или чего-то подобного можно легко определить направление потока в точке. Вместо того, чтобы напрямую определять векторный поток, часто более интуитивно понятно указать некоторые его свойства. Более того, по этим свойствам в любом случае можно однозначно определить поток.

Если поток j проходит через область под углом θ к нормали площади $\mathbf {\hat {n}}$ , то скалярное произведение

\mathbf {j} \cdot \mathbf {\hat {n}} =j\cos \theta .

То есть составляющая потока, проходящего через поверхность (т.е. нормальная к ней), равна j cos θ , тогда как составляющая потока, проходящего по касательной к этой области, равна j sin θ , но нет потока, фактически проходящего через область в тангенциальном направлении, . направление. Единственная составляющая потока , проходящая нормально к площади, - это косинусная составляющая.

Для векторного потока поверхностный интеграл от j по поверхности S дает правильное течение в единицу времени через поверхность:

{\frac {\mathrm {d} q}{\mathrm {d} t}}=\iint _{S}\mathbf {j} \cdot \mathbf {\hat {n}} \,dA=\iint _{S}\mathbf {j} \cdot d\mathbf {A} ,

где A (и его бесконечно малая величина) — это площадь вектора — комбинация

\mathbf {A} =A\mathbf {\hat {n}}

величины площади A, через которую проходит объект, и единичного вектора

\mathbf {\hat {n}}

нормально для этого района.В отличие от второй системы уравнений, поверхность здесь не обязательно должна быть плоской.

Наконец, мы можем снова интегрировать по времени от t ₁ до t ₂ , получая общее количество имущества, протекающего через поверхность за это время ( t ₂ − t ₁ ):

q=\int _{t_{1}}^{t_{2}}\iint _{S}\mathbf {j} \cdot d\mathbf {A} \,dt.

Транспортные потоки [ править ]

Восемь наиболее распространенных форм потоков в литературе по явлениям переноса определяются следующим образом:

Поток импульса , скорость передачи импульса через единицу площади (Н·с·м ⁻²·с ⁻¹). ( Закон вязкости Ньютона ) ^[7]
Тепловой поток , скорость теплового потока через единицу площади (Дж·м ⁻²·с ⁻¹). ( Закон проводимости Фурье ) ^[8] (Это определение теплового потока соответствует первоначальному определению Максвелла.) ^[5]
Диффузионный поток , скорость движения молекул через единицу площади (моль·м ⁻²·с ⁻¹). ( Закон диффузии Фика ) ^[7]
Объемный поток , скорость объемного потока через единицу площади (м ³·м ⁻²·с ⁻¹). ( Закон Дарси о движении грунтовых вод )
Массовый поток , скорость массового расхода через единицу площади (кг·м ⁻²·с ⁻¹). (Либо альтернативная форма закона Фика, включающая молекулярную массу, либо альтернативная форма закона Дарси, включающая плотность.)
Поток излучения — количество энергии, передаваемой в виде фотонов на определенном расстоянии от источника на единицу площади в секунду (Дж·м ⁻²·с ⁻¹). Используется в астрономии для определения величины и спектрального класса звезды. Также действует как обобщение теплового потока, который равен потоку излучения, если ограничить его электромагнитным спектром.
Поток энергии , скорость передачи энергии через единицу площади (Дж·м ⁻²·с ⁻¹). Радиационный поток и тепловой поток являются частными случаями потока энергии.
Поток частиц , скорость переноса частиц через единицу площади ([количество частиц] м ⁻²·с ⁻¹)

Эти потоки представляют собой векторы в каждой точке пространства и имеют определенную величину и направление. любого из этих потоков можно Также по дивергенции определить скорость накопления величины в контрольном объеме вокруг данной точки пространства. Для несжимаемого потока дивергенция объемного потока равна нулю.

диффузия Химическая

Как упоминалось выше, химический молярный поток компонента А в изотермической изобарной системе определяется в законе диффузии Фика как:

\mathbf {J} _{A}=-D_{AB}\nabla c_{A}

где символ наблы ∇ обозначает оператор градиента , D _AB — коэффициент диффузии (m ²·с ⁻¹) компонента A, диффундирующего через компонент B, c _A — концентрация ( моль /м ³) компонента А. ^[9]

Этот поток имеет единицы моль·м. ⁻²·с ⁻¹и соответствует первоначальному определению потока Максвелла. ^[5]

Для разбавленных газов кинетическая молекулярная теория связывает коэффициент диффузии D с плотностью частиц n = N / V , молекулярной массой m столкновения , сечением $\sigma$ , а абсолютная температура T на

D={\frac {2}{3n\sigma }}{\sqrt {\frac {kT}{\pi m}}}

где второй множитель — это длина свободного пробега , а квадратный корень (с постоянной Больцмана k ) — средняя скорость частиц.

В турбулентных потоках перенос за счет вихревого движения можно выразить как резко увеличенный коэффициент диффузии.

Квантовая механика [ править ]

В квантовой механике частицы массы m в квантовом состоянии ψ ( r , t ) имеют плотность вероятности, определяемую как

\rho =\psi ^{*}\psi =|\psi |^{2}.

Таким образом, вероятность найти частицу в дифференциальном элементе объема d ³р это

dP=|\psi |^{2}\,d^{3}\mathbf {r} .

Тогда число частиц, проходящих перпендикулярно через единицу площади поперечного сечения в единицу времени, является потоком вероятности;

\mathbf {J} ={\frac {i\hbar }{2m}}\left(\psi \nabla \psi ^{*}-\psi ^{*}\nabla \psi \right).

Иногда это называют вероятностным током или плотностью тока. ^[10] или плотность потока вероятности. ^[11]

поверхностный интеграл Поток как

Общее математическое определение (поверхностный интеграл) [ править ]

В качестве математической концепции поток представлен поверхностным интегралом векторного поля : ^[12]

\Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathrm {d} \mathbf {A}

\Phi _{F}=\iint _{A}\mathbf {F} \cdot \mathbf {n} \,\mathrm {d} A

где F — векторное поле , а d A — векторная площадь поверхности A , направленная по нормали к поверхности . Во втором случае n — направленный наружу единичный вектор нормали к поверхности.

Поверхность должна быть ориентируемой , т. е. можно выделить две стороны: поверхность не сворачивается сама на себя. Кроме того, поверхность должна быть действительно ориентирована, т. е. мы используем соглашение о том, какое направление течения считается положительным; течение обратного потока тогда считается отрицательным.

Нормаль к поверхности обычно определяется по правилу правой руки .

И наоборот, можно считать поток более фундаментальной величиной и называть векторное поле плотностью потока.

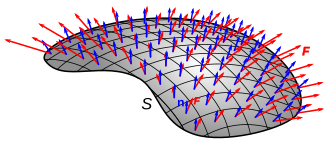
Часто векторное поле рисуется кривыми (линиями поля), идущими по «течению»; тогда величина векторного поля — это плотность линий, а поток через поверхность — это количество линий. Линии берут начало в областях положительной дивергенции (источники) и заканчиваются в областях отрицательной дивергенции (стоки).

См. также изображение справа: количество красных стрелок, проходящих через единицу площади, представляет собой плотность потока, кривая, описывающая красные стрелки, обозначает границу поверхности, а ориентация стрелок относительно поверхности обозначает знак скалярное произведение векторного поля с нормалями поверхности.

Если поверхность охватывает трехмерную область, обычно поверхность ориентирована так, что приток считается положительным; обратное – отток .

Теорема о дивергенции утверждает, что чистый отток через замкнутую поверхность, другими словами, чистый отток из трехмерной области, находится путем сложения локального чистого оттока из каждой точки области (который выражается дивергенцией ) .

Если поверхность не замкнута, то ее границей является ориентированная кривая. Теорема Стокса утверждает, что поток ротора векторного поля представляет собой линейный интеграл векторного поля по этой границе. Этот интеграл по траекториям также называется циркуляцией , особенно в гидродинамике. Таким образом, ротор – это плотность циркуляции.

Мы можем применить поток и эти теоремы ко многим дисциплинам, в которых мы видим токи, силы и т. д., действующие через области.

Электромагнетизм [ править ]

Электрический поток [ править ]

Электрический «заряд», такой как одиночный протон в космосе, имеет величину, определяемую в кулонах. Вокруг такого заряда существует электрическое поле. В наглядной форме электрическое поле положительного точечного заряда можно представить как точку, излучающую линии электрического поля (иногда также называемые «силовыми линиями»). Концептуально электрический поток можно рассматривать как «количество силовых линий», проходящих через данную область. Математически электрический поток представляет собой интеграл нормальной составляющей электрического поля на заданной площади. Следовательно, единицами электрического потока в системе MKS являются на ньютоны кулон , умноженные на квадратные метры, или Н·м. ²/С. (Плотность электрического потока представляет собой электрический поток на единицу площади и является мерой напряженности нормальной составляющей электрического поля, усредненной по площади интегрирования. Ее единицами являются N/C, такие же, как и электрическое поле в единицах MKS. )

две формы электрического потока Используются , одна для электрического поля: ^[13]^[14]

\Phi _{E}=

$\оинт$

{\scriptstyle A}

\mathbf {E} \cdot {\rm {d}}\mathbf {A}

и один для D -поля (называемый электрическим смещением ):

\Phi _{D}=

$\оинт$

{\scriptstyle A}

\mathbf {D} \cdot {\rm {d}}\mathbf {A}

Эта величина возникает в законе Гаусса , который гласит, что поток электрического поля E из замкнутой поверхности пропорционален электрическому заряду Q _A, заключенному в поверхности (независимо от того, как этот заряд распределен), интегральная форма:

$\оинт$

{\scriptstyle A}

\mathbf {E} \cdot {\rm {d}}\mathbf {A} ={\frac {Q_{A}}{\varepsilon _{0}}}

где ε ₀ — диэлектрическая проницаемость свободного пространства .

Если рассмотреть поток вектора электрического поля E для трубки вблизи точечного заряда в поле заряда, но не содержащей его со сторонами, образованными линиями, касающимися поля, то поток для сторон равен нулю и существует равный и противоположный поток на обоих концах трубки. Это следствие закона Гаусса, примененного к полю обратных квадратов. Поток для любой поверхности поперечного сечения трубки будет одинаковым. Полный поток для любой поверхности, окружающей заряд q, равен q / ε ₀ . ^[15]

В свободном пространстве электрическое смещение задается определяющим соотношением D = ε ₀ E , поэтому для любой ограничивающей поверхности поток D -поля равен заряду Q _A внутри нее. Здесь выражение «поток» указывает на математическую операцию и, как видно, результат не обязательно является «потоком», поскольку на самом деле ничто не течет вдоль силовых линий электрического поля.

Магнитный поток [ править ]

Плотность магнитного потока ( магнитного поля ), имеющая единицу Вб/м ² ( Тесла ) обозначается B , а магнитный поток определяется аналогично: ^[13]^[14]

\Phi _{B}=\iint _{A}\mathbf {B} \cdot \mathrm {d} \mathbf {A}

с теми же обозначениями, что и выше. Величина возникает в законе индукции Фарадея , где магнитный поток зависит от времени либо потому, что граница зависит от времени, либо магнитное поле зависит от времени. В интегральной форме:

-{\frac {{\rm {d}}\Phi _{B}}{{\rm {d}}t}}=\oint _{\partial A}\mathbf {E} \cdot d{\boldsymbol {\ell }}

где d ℓ - бесконечно малый векторный элемент замкнутой кривой. $\partial A$ , с величиной, равной длине бесконечно малого линейного элемента, и направлением, заданным касательной к кривой $\partial A$ , знак которого определяется направлением интегрирования.

Скорость изменения магнитного потока через петлю провода минус электродвижущая сила, созданная в этом проводе. Направление таково, что если позволить току проходить по проводу, электродвижущая сила вызовет ток, который «противодействует» изменению магнитного поля, сам по себе создавая магнитное поле, противоположное этому изменению. Это основа катушек индуктивности и многих электрических генераторов .

Пойнтинг Флюс [ править ]

Используя это определение, поток вектора Пойнтинга S над заданной поверхностью — это скорость, с которой электромагнитная энергия течет через эту поверхность, определяемая, как и раньше: ^[14]

\Phi _{S}=

$\оинт$

{\scriptstyle A}

\mathbf {S} \cdot {\rm {d}}\mathbf {A}

Поток вектора Пойнтинга через поверхность — это электромагнитная мощность или энергия в единицу времени , проходящая через эту поверхность. Это обычно используется при анализе электромагнитного излучения , но применимо и к другим электромагнитным системам.

Как ни странно, вектор Пойнтинга иногда называют потоком мощности , что является примером первого использования потока, приведенного выше. ^[16] Он имеет единицы измерения ватт на квадратный метр (Вт/м). ²).

Единицы радиометрии СИ [ править ]

Радиометрические установки СИ
v
т
и
Количество		Единица		Измерение	Примечания
Имя	Символ ^{[номер 1]}	Имя	Символ	Измерение	Примечания
Лучистая энергия	$Вопрос е$ ^{[номер 2]}	джоуль	Дж	M ⋅ L ²⋅ T ⁻²	Энергия электромагнитного излучения.
Плотность лучистой энергии	$мы $	Джоуль на кубический метр	Дж/м ³	M ⋅ L ⁻¹⋅ T ⁻²	Лучистая энергия на единицу объема.
Лучистый поток	$Φ е$ ^{[номер 2]}	ватт	Вт = Дж/с	M ⋅ L ²⋅ T ⁻³	Лучистая энергия, излучаемая, отражаемая, передаваемая или принимаемая в единицу времени. Иногда ее также называют «силой излучения» и в астрономии называют светимостью .
Спектральный поток	$Ф е, н$ ^{[номер 3]}	ватт на герц	Вт/ Гц	M ⋅ L ²⋅ T ⁻²	Лучистый поток на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅нм. ⁻¹.
Спектральный поток	$Ф е, л$ ^{[номер 4]}	ватт на метр	Вт/м	M ⋅ L ⋅ T ⁻³
Интенсивность излучения	$Для него Ом$ ^{[номер 5]}	ватты на стерадиан	с сэром	M ⋅ L ²⋅ T ⁻³	Лучистый поток, излучаемый, отраженный, передаваемый или принимаемый, на единицу телесного угла. Это направленная величина.
Спектральная интенсивность	$To e, Ω, ν$ ^{[номер 3]}	ватты на стерадиан на герц	W⋅sr ⁻¹⋅Hz ⁻¹	M ⋅ L ²⋅ T ⁻²	Интенсивность излучения на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr. ⁻¹⋅nm ⁻¹. Это направленная величина.
Спектральная интенсивность	$Чтобы е, Ω, λ$ ^{[номер 4]}	ватт на стерадиан на метр	W⋅sr ⁻¹⋅m ⁻¹	M ⋅ L ⋅ T ⁻³
Сияние	$L e,Ом$ ^{[номер 5]}	ватт на стерадиан на квадратный метр	W⋅sr ⁻¹⋅m ⁻²	M ⋅ T ⁻³	Лучистый поток, излучаемый, отраженный, передаваемый или принимаемый поверхностью , на единицу телесного угла на единицу проецируемой площади. Это направленная величина. Иногда это также ошибочно называют «интенсивностью».
Спектральное сияние Удельная интенсивность	$Л е, О, н$ ^{[номер 3]}	ватт на стерадиан на квадратный метр на герц	W⋅sr ⁻¹⋅m ⁻²⋅Hz ⁻¹	M ⋅ T ⁻²	Сияние поверхности на единицу частоты или длины волны. Последний обычно измеряется в W⋅sr. ⁻¹⋅m ⁻²⋅nm ⁻¹. Это направленная величина. Иногда это также ошибочно называют «спектральной интенсивностью».
Спектральное сияние Удельная интенсивность	$Л е, о, л$ ^{[номер 4]}	ватт на стерадиан на квадратный метр, на метр	W⋅sr ⁻¹⋅m ⁻³	M ⋅ L ⁻¹⋅ T ⁻³
Освещенность Плотность потока	$Э е$ ^{[номер 2]}	ватт на квадратный метр	Вт/м ²	M ⋅ T ⁻³	Лучистый поток, на единицу воспринимаемый поверхностью площади. Иногда это также ошибочно называют «интенсивностью».
Спектральное излучение Спектральная плотность потока	$Э е, н$ ^{[номер 3]}	ватт на квадратный метр на герц	W⋅m ⁻²⋅Hz ⁻¹	M ⋅ T ⁻²	Освещенность поверхности на единицу частоты или длины волны. Иногда это также ошибочно называют «спектральной интенсивностью». Единицы спектральной плотности потока, не относящиеся к системе СИ, включают янский ( 1 Ян = 10 ⁻²⁶ W⋅m ⁻²⋅Hz ⁻¹) и единица солнечного потока ( 1 sfu = 10 ⁻²² W⋅m ⁻²⋅Hz ⁻¹ = 10 ⁴ Ты ).
Спектральное излучение Спектральная плотность потока	$Угорь $ ^{[номер 4]}	ватт на квадратный метр, на метр	Вт/м ³	M ⋅ L ⁻¹⋅ T ⁻³
Радиосити	$J Да$ ^{[номер 2]}	ватт на квадратный метр	Вт/м ²	M ⋅ T ⁻³	Лучистый поток, покидающий (излучаемый, отражаемый и передаваемый) поверхность на единицу площади. Иногда это также ошибочно называют «интенсивностью».
Спектральная радиация	$I е, ν$ ^{[номер 3]}	ватт на квадратный метр на герц	W⋅m ⁻²⋅Hz ⁻¹	M ⋅ T ⁻²	Излучение поверхности на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅м. ⁻²⋅nm ⁻¹. Иногда это также ошибочно называют «спектральной интенсивностью».
Спектральная радиация	$I е, λ$ ^{[номер 4]}	ватт на квадратный метр, на метр	Вт/м ³	M ⋅ L ⁻¹⋅ T ⁻³
Сияющее великолепие	$Мне $ ^{[номер 2]}	ватт на квадратный метр	Вт/м ²	M ⋅ T ⁻³	Лучистый поток, на единицу излучаемый поверхностью площади. Это излучаемая составляющая излучательности. «Излучение излучения» — старый термин для этой величины. Иногда это также ошибочно называют «интенсивностью».
Спектральная яркость	$М е, ν$ ^{[номер 3]}	ватт на квадратный метр на герц	W⋅m ⁻²⋅Hz ⁻¹	M ⋅ T ⁻²	Светимость поверхности на единицу частоты или длины волны. Последний обычно измеряется в Вт⋅м. ⁻²⋅nm ⁻¹. «Спектральный эмиттанс» — старый термин для этой величины. Иногда это также ошибочно называют «спектральной интенсивностью».
Спектральная яркость	$М е, λ$ ^{[номер 4]}	ватт на квадратный метр, на метр	Вт/м ³	M ⋅ L ⁻¹⋅ T ⁻³
Лучистое воздействие	$Он $	Джоуль на квадратный метр	Дж/м ²	M ⋅ T ⁻²	Лучистая энергия, полученная поверхностью на единицу площади, или, что эквивалентно, освещенность поверхности , интегрированная во времени облучения. Иногда это также называют «лучистой плотностью».
Спектральная экспозиция	$H e, ν$ ^{[номер 3]}	Джоуль на квадратный метр на герц	J⋅m ⁻²⋅Hz ⁻¹	M ⋅ T ⁻¹	Лучистая экспозиция поверхности на единицу частоты или длины волны. Последний обычно измеряется в Дж⋅м. ⁻²⋅nm ⁻¹. Иногда это также называют «спектральной флюенсом».
Спектральная экспозиция	$He, λ$ ^{[номер 4]}	джоуль на квадратный метр, на метр	Дж/м ³	M ⋅ L ⁻¹⋅ T ⁻²
См. также: И Радиометрия Фотометрия

^ Организации по стандартизации рекомендуют обозначать радиометрические величины суффиксом «e» (от «энергетические»), чтобы избежать путаницы с фотометрическими или фотонными величинами.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Иногда встречаются альтернативные символы: $W$ или $E$ для энергии излучения, $P$ или $F$ для потока излучения, $I$ для освещенности, $W$ для мощности излучения.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Спектральные величины, приведенные на единицу частоты, обозначаются суффиксом « ν » (греческая буква nu , не путать с буквой «v», обозначающей фотометрическую величину).
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Спектральные величины, приведённые на единицу длины волны, обозначаются суффиксом « λ ».
↑ Перейти обратно: Перейти обратно: ^а ^б Направленные величины обозначаются суффиксом « Ом ».

См. также [ править ]

Величины AB
Генератор сжатия потока со взрывной накачкой
Поток вихревой ковариации (также известный как вихревая корреляция, вихревой поток)
Испытательная установка для быстрого флюса
Флюенс (поток первого рода для пучков частиц)
Гидродинамика
След потока
Закрепление флюса
Квантование потока
Закон Гаусса
Закон обратных квадратов
Янский (единица спектральной плотности потока вне системы СИ)
Скрытый тепловой поток
Световой поток
Магнитный поток
Квант магнитного потока
Нейтронный поток
Пойнтинг-флюс
Теорема Пойнтинга
Лучистый поток
Быстрый одиночный квант потока
Поток звуковой энергии
Объемный поток (поток первого рода для жидкостей)
Объемный расход (поток второго рода для жидкостей)

Примечания [ править ]

^ Перселл, с. 22-26
^ Уикли, Эрнест (1967). Этимологический словарь современного английского языка . Публикации Courier Dover. п. 581. ИСБН 0-486-21873-2 .
^ Херивел, Джон (1975). Жозеф Фурье: человек и физик . Оксфорд: Кларендон Пресс. стр. 181–191. ISBN 0-19-858149-1 .
^ Фурье, Жозеф (1822). Аналитическая теория теплоты (на французском языке). Париж: Firmin Didot Père et Fils. ОСЛК 2688081 .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Максвелл, Джеймс Клерк (1892). Трактат об электричестве и магнетизме . ISBN 0-486-60636-8 .
^ Берд, Р. Байрон ; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (1960). Транспортные явления . Уайли. ISBN 0-471-07392-Х .
↑ Перейти обратно: Перейти обратно: ^а ^б премьер-министр Уилан; М. Дж. Ходжсон (1978). Основные принципы физики (2-е изд.). Джон Мюррей. ISBN 0-7195-3382-1 .
^ Карслоу, HS; Джагер, JC (1959). Теплопроводность в твердых телах (второе изд.). Издательство Оксфордского университета. ISBN 0-19-853303-9 .
^ Велти; Уикс, Уилсон и Роррер (2001). Основы импульса, тепла и массообмена (4-е изд.). Уайли. ISBN 0-471-38149-7 .
^ Д. МакМахон (2008). Квантовая механика демистифицирована (2-е изд.). Мак Грау Хилл. ISBN 978-0-07-145546-6 .
^ Сакураи, Джей-Джей (1967). Продвинутая квантовая механика . Эддисон Уэсли. ISBN 0-201-06710-2 .
^ Мюррей Р. Шпигель; С. Липшуц; Д. Спеллман (2009). Векторный анализ . Очерки Шаума (2-е изд.). МакГроу Хилл. п. 100. ИСБН 978-0-07-161545-7 .
↑ Перейти обратно: Перейти обратно: ^а ^б ИС Грант; В. Р. Филлипс (2008). Электромагнетизм . Манчестерская физика (2-е изд.). Джон Уайли и сыновья . ISBN 978-0-471-92712-9 .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Диджей Гриффитс (2007). Введение в электродинамику (3-е изд.). Pearson Education, Дорлинг Киндерсли . ISBN 978-81-7758-293-2 .
^ Лекции Фейнмана по физике Том. II гл. 4: Электростатика
^ Вангснесс, Роальд К. (1986). Электромагнитные поля (2-е изд.). Уайли. ISBN 0-471-81186-6 . стр.357

Браун, Майкл (2010). Физика для техники и науки, 2-е издание . Очертания Шаума. Нью-Йорк, Торонто: Издательство McGraw-Hill . ISBN 978-0-0716-1399-6 .
Перселл, Эдвард (2013). Электричество и магнетизм, 3-е издание . Кембридж, Великобритания: Издательство Кембриджского университета . ISBN 978110-7014022 .

Дальнейшее чтение [ править ]

Стауффер, PH (2006). «Флюс в замешательстве: предложение по последовательному использованию» . Грунтовые воды . 44 (2): 125–128. Бибкод : 2006GrWat..44..125S . дои : 10.1111/j.1745-6584.2006.00197.x . ПМИД 16556188 . S2CID 21812226 .

Внешние ссылки [ править ]

Словарное определение потока в Викисловаре

[note-suffix-e-17] Организации по стандартизации рекомендуют обозначать радиометрические величины суффиксом «e» (от «энергетические»), чтобы избежать путаницы с фотометрическими или фотонными величинами.

[note-alternative-symbol-radiometric-18] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и Иногда встречаются альтернативные символы: $W$ или $E$ для энергии излучения, $P$ или $F$ для потока излучения, $I$ для освещенности, $W$ для мощности излучения.

[note-suffix-nu-19] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Спектральные величины, приведенные на единицу частоты, обозначаются суффиксом « ν » (греческая буква nu , не путать с буквой «v», обозначающей фотометрическую величину).

[note-suffix-lambda-20] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Спектральные величины, приведённые на единицу длины волны, обозначаются суффиксом « λ ».

[note-suffix-omega-21] Перейти обратно: Перейти обратно: ^а ^б Направленные величины обозначаются суффиксом « Ом ».

[1] Перселл, с. 22-26

[2] Уикли, Эрнест (1967). Этимологический словарь современного английского языка . Публикации Courier Dover. п. 581. ИСБН 0-486-21873-2 .

[3] Херивел, Джон (1975). Жозеф Фурье: человек и физик . Оксфорд: Кларендон Пресс. стр. 181–191. ISBN 0-19-858149-1 .

[4] Фурье, Жозеф (1822). Аналитическая теория теплоты (на французском языке). Париж: Firmin Didot Père et Fils. ОСЛК 2688081 .

[Maxwell-5] Перейти обратно: Перейти обратно: ^а ^б ^с Максвелл, Джеймс Клерк (1892). Трактат об электричестве и магнетизме . ISBN 0-486-60636-8 .

[6] Берд, Р. Байрон ; Стюарт, Уоррен Э.; Лайтфут, Эдвин Н. (1960). Транспортные явления . Уайли. ISBN 0-471-07392-Х .

[Physics_P.M-7] Перейти обратно: Перейти обратно: ^а ^б премьер-министр Уилан; М. Дж. Ходжсон (1978). Основные принципы физики (2-е изд.). Джон Мюррей. ISBN 0-7195-3382-1 .

[8] Карслоу, HS; Джагер, JC (1959). Теплопроводность в твердых телах (второе изд.). Издательство Оксфордского университета. ISBN 0-19-853303-9 .

[9] Велти; Уикс, Уилсон и Роррер (2001). Основы импульса, тепла и массообмена (4-е изд.). Уайли. ISBN 0-471-38149-7 .

[10] Д. МакМахон (2008). Квантовая механика демистифицирована (2-е изд.). Мак Грау Хилл. ISBN 978-0-07-145546-6 .

[11] Сакураи, Джей-Джей (1967). Продвинутая квантовая механика . Эддисон Уэсли. ISBN 0-201-06710-2 .

[12] Мюррей Р. Шпигель; С. Липшуц; Д. Спеллман (2009). Векторный анализ . Очерки Шаума (2-е изд.). МакГроу Хилл. п. 100. ИСБН 978-0-07-161545-7 .

[Electromagnetism_2008-13] Перейти обратно: Перейти обратно: ^а ^б ИС Грант; В. Р. Филлипс (2008). Электромагнетизм . Манчестерская физика (2-е изд.). Джон Уайли и сыновья . ISBN 978-0-471-92712-9 .

[Electrodynamics_2007-14] Перейти обратно: Перейти обратно: ^а ^б ^с Диджей Гриффитс (2007). Введение в электродинамику (3-е изд.). Pearson Education, Дорлинг Киндерсли . ISBN 978-81-7758-293-2 .

[15] Лекции Фейнмана по физике Том. II гл. 4: Электростатика

[16] Вангснесс, Роальд К. (1986). Электромагнитные поля (2-е изд.). Уайли. ISBN 0-471-81186-6 . стр.357

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[номер 1]

[номер 2]

[номер 3]

[номер 4]

[номер 5]

Терминология [ править ]

Поток как скорость потока на единицу площади [ править ]

Общее математическое определение (транспорт) [ править ]

Свойства [ править ]

Транспортные потоки [ править ]

диффузия Химическая ​ ​

Квантовая механика [ править ]

поверхностный интеграл Поток как

Общее математическое определение (поверхностный интеграл) [ править ]

Электромагнетизм [ править ]

Электрический поток [ править ]

Магнитный поток [ править ]

Пойнтинг Флюс [ править ]

Единицы радиометрии СИ [ править ]

См. также [ править ]

Примечания [ править ]

Дальнейшее чтение [ править ]

Внешние ссылки [ править ]

диффузия Химическая