Основная теорема исчисления

Фундаментальная теорема исчисления — это теорема , которая связывает концепцию дифференцирования функции . (вычисление ее наклонов или скорости изменения в каждый момент времени) с концепцией интегрирования функции (вычисление площади под ее графиком или кумулятивного эффекта) небольших взносов). Эти две операции являются обратными друг другу, за исключением постоянного значения, которое зависит от того, где начинается вычисление площади.

Первая часть теоремы, первая фундаментальная теорема исчисления , утверждает, что для непрерывной функции $f$ первообразная F или неопределенный интеграл $может$ быть получен как интеграл от $f$ на интервале с переменной верхней границей. ^[1]

И наоборот, вторая часть теоремы, вторая фундаментальная теорема исчисления , утверждает, что интеграл функции $f$ на фиксированном интервале равен изменению любой первообразной $F$ между концами интервала. Это значительно упрощает вычисление определенного интеграла при условии, что первообразная может быть найдена путем символического интегрирования , что позволяет избежать численного интегрирования .

История [ править ]

Фундаментальная теорема исчисления связывает дифференцирование и интегрирование, показывая, что эти две операции по сути являются обратными друг другу. До открытия этой теоремы не признавалось, что эти две операции связаны. Древнегреческие математики знали, как вычислить площадь с помощью бесконечно малых чисел — операцию, которую мы сейчас назвали бы интегрированием. Истоки дифференциации также появились на сотни лет раньше фундаментальной теоремы исчисления; например, в четырнадцатом веке понятия непрерывности функций и движения изучались оксфордскими калькуляторами и другими учеными. Историческая значимость фундаментальной теоремы исчисления заключается не в способности вычислять эти операции, а в осознании того, что две, казалось бы, разные операции (вычисление геометрических площадей и вычисление градиентов) на самом деле тесно связаны.

С гипотезы и доказательства основной теоремы исчисления начинается исчисление как единая теория интегрирования и дифференцирования. Первое опубликованное утверждение и доказательство элементарной формы фундаментальной теоремы, строго геометрического характера. ^[2] был Джеймс Грегори (1638–1675). ^[3]^[4] Исаак Барроу (1630–1677) доказал более обобщенную версию теоремы: ^[5]а его ученик Исаак Ньютон (1642–1727) завершил разработку окружающей математической теории. Готфрид Лейбниц (1646–1716) систематизировал эти знания в виде расчета бесконечно малых величин и ввел обозначения, используемые сегодня.

Геометрический смысл/Доказательство [ править ]

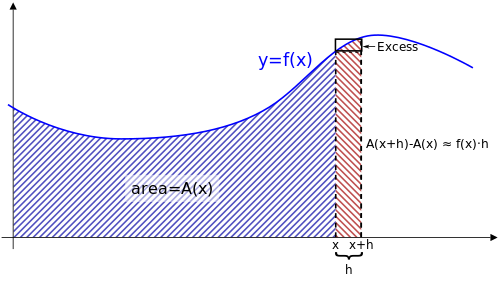
Первую фундаментальную теорему можно интерпретировать следующим образом. Учитывая непрерывную функцию $y=f(x)$ график которого представлен в виде кривой, определяется соответствующая «функция площади». $x\mapsto A(x)$ такой, что $A (x)$ — это площадь под кривой между $0$ и $x$ . Площадь $A (x)$ может быть нелегко вычислить, но предполагается, что она четко определена.

Площадь под кривой между $x$ и $x + h$ можно вычислить, найдя площадь между $0$ и $x + h$ , а затем вычитая площадь между $0$ и $x$ . Другими словами, площадь этой «полосы» будет равна $A (x + h) - A (x)$ .

Есть и другой способ оценить площадь этой же полосы. Как показано на сопроводительном рисунке, $h$ умножается на $f (x)$ , чтобы найти площадь прямоугольника, размер которого примерно равен этой полосе. Так:

A(x+h)-A(x)\approx f(x)\cdot h

Разделив на h обе части, получим:

{\frac {A(x+h)-A(x)}{h}}\ \approx f(x)

Эта оценка становится идеальным равенством, когда h приближается к 0:

f(x)=\lim _{h\to 0}{\frac {A(x+h)-A(x)}{h}}\ {\stackrel {\text{def}}{=}}\ A'(x).

То есть производная функции площади

A (x)

существует и равна исходной функции

f (x)

, поэтому функция площади является первообразной исходной функции.

Таким образом, производная интеграла функции (площади) является исходной функцией, так что производная и интеграл являются обратными операциями , обращающими друг друга. В этом суть Основной теоремы.

Физическая интуиция [ править ]

Интуитивно фундаментальная теорема утверждает, что интегрирование и дифференцирование — это обратные операции, которые обращают друг друга.

Вторая фундаментальная теорема гласит, что сумма бесконечно малых изменений количества (интеграл от производной количества) составляет чистое изменение количества. Чтобы представить себе это, представьте, что вы путешествуете на машине и хотите узнать пройденное расстояние (чистое изменение положения на шоссе). Вы можете видеть скорость на спидометре, но не можете посмотреть на свое местоположение. Каждую секунду вы можете узнать, какое расстояние проехал автомобиль, используя $расстояние = скорость \times время$ , то есть умножив текущую скорость (в километрах или милях в час) на временной интервал (1 секунда = ${\tfrac {1}{3600}}$ час). Суммируя все эти маленькие шаги, вы можете примерно оценить общее пройденное расстояние, даже не глядя за пределы автомобиля:

{\text{distance traveled}}=\sum \left({\begin{array}{c}{\text{velocity at}}\\{\text{each time}}\end{array}}\right)\times \left({\begin{array}{c}{\text{time}}\\{\text{interval}}\end{array}}\right)=\sum v_{t}\times \Delta t.

Как

\Delta t

становится бесконечно малым, то суммирование соответствует интегрированию . Таким образом, интеграл функции скорости (производная положения) вычисляет, какое расстояние проехал автомобиль (чистое изменение положения).

Первая фундаментальная теорема гласит, что значение любой функции — это скорость изменения (производная) ее интеграла от фиксированной начальной точки до любой выбранной конечной точки. Продолжая приведенный выше пример, используя скорость в качестве функции, вы можете проинтегрировать ее от начального момента до любого заданного момента времени, чтобы получить функцию расстояния, производной которой является эта скорость. (Чтобы получить положение маркера шоссе, вам нужно будет добавить к этому интегралу исходное положение и принять во внимание, было ли ваше путешествие в направлении увеличения или уменьшения маркеров миль.)

Официальные заявления [ править ]

Теорема состоит из двух частей. В первой части рассматривается производная от первообразной , а во второй части рассматривается связь между первообразными и определенными интегралами .

Первая часть [ править ]

Эту часть иногда называют первой фундаментальной теоремой исчисления . ^[6]

Пусть $f$ — непрерывная вещественная функция, определенная на замкнутом интервале $[a, b]$ . Пусть $F$ — функция, определенная для всех $x$ в $[a, b]$ формулой

F(x)=\int _{a}^{x}f(t)\,dt.

Тогда $F$ на равномерно непрерывен [ $a, b] и$ дифференцируем на открытом интервале $(a, b)$ , и

F'(x)=f(x)

для всех

x

в

(a, b)

, поэтому

F

является первообразной

f

.

Следствие [ править ]

Фундаментальная теорема часто используется для вычисления определенного интеграла функции. $f$ для которой первообразная $F$ известен. В частности, если $f$ является вещественной непрерывной функцией на $[a,b]$ и $F$ является первообразной от $f$ в $[a,b]$ , затем

\int _{a}^{b}f(t)\,dt=F(b)-F(a).

Следствие предполагает непрерывность на всем интервале. Этот результат несколько усиливается в следующей части теоремы.

Вторая часть [ править ]

Эту часть иногда называют второй фундаментальной теоремой исчисления. ^[7] или теорема Ньютона-Лейбница .

Позволять $f$ быть вещественной функцией на замкнутом интервале $[a,b]$ и $F$ непрерывная функция на $[a,b]$ который является первообразным от $f$ в $(a,b)$ :

F'(x)=f(x).

Если $f$ интегрируем ли Риман на $[a,b]$ затем

\int _{a}^{b}f(x)\,dx=F(b)-F(a).

Вторая часть несколько сильнее следствия, поскольку не предполагает, что $f$ является непрерывным.

Когда первообразная $F$ из $f$ существует, то существует бесконечно много первообразных для $f$ , полученный добавлением произвольной константы к $F$ . Кроме того, по первой части теоремы первообразные $f$ всегда существовать, когда $f$ является непрерывным.

Доказательство первой части [ править ]

Для данной функции $f$ определите функцию $F (x)$ как

F(x)=\int _{a}^{x}f(t)\,dt.

Для любых двух чисел $x 1$ и $x 1 + Δ x$ в $[a, b]$ мы имеем

{\begin{aligned}F(x_{1}+\Delta x)-F(x_{1})&=\int _{a}^{x_{1}+\Delta x}f(t)\,dt-\int _{a}^{x_{1}}f(t)\,dt\\&=\int _{x_{1}}^{x_{1}+\Delta x}f(t)\,dt,\end{aligned}}

последнее равенство вытекает из основных свойств интегралов и аддитивности площадей.

Согласно теореме о среднем значении для интегрирования существует действительное число $c\in [x_{1},x_{1}+\Delta x]$ такой, что

\int _{x_{1}}^{x_{1}+\Delta x}f(t)\,dt=f(c)\cdot \Delta x.

Следует, что

F(x_{1}+\Delta x)-F(x_{1})=f(c)\cdot \Delta x,

и таким образом, что

{\frac {F(x_{1}+\Delta x)-F(x_{1})}{\Delta x}}=f(c).

Принимая предел как $\Delta x\to 0,$ и имея в виду, что $c\in [x_{1},x_{1}+\Delta x],$ каждый получает

\lim _{\Delta x\to 0}{\frac {F(x_{1}+\Delta x)-F(x_{1})}{\Delta x}}=\lim _{\Delta x\to 0}f(c),

то есть,

F'(x_{1})=f(x_{1}),

согласно определению производной, непрерывности

f

и теореме о сжатии . ^[8]

Доказательство следствия [ править ]

Предположим, $F$ является первообразной $f$ , причем $f$ непрерывна на $[a, b]$ . Позволять

G(x)=\int _{a}^{x}f(t)\,dt.

По первой части теоремы мы знаем, что $G$ также является первообразной $f$ . Поскольку $F' - G' = 0,$ из теоремы о среднем значении следует, что $F - G$ является постоянной функцией , то есть существует число $c$ такое, что $G (x) = F (x) + c$ для всех $x$ в $[a, б]$ . Полагая $x = a$ , мы имеем

F(a)+c=G(a)=\int _{a}^{a}f(t)\,dt=0,

что означает

c знак равно - F (а)

. Другими словами,

G (x) = F (x) - F (a)

, и поэтому

\int _{a}^{b}f(x)\,dx=G(b)=F(b)-F(a).

Доказательство второй части [ править ]

Это предельное доказательство с помощью сумм Римана .

Для начала напомним теорему о среднем значении . Короче говоря, если $F$ непрерывно на замкнутом интервале $[a, b]$ и дифференцируемо на открытом интервале $(a, b)$ , то существует некоторый $c$ в $(a, b)$ такой, что

F'(c)(b-a)=F(b)-F(a).

Пусть $f$ (по Риману) интегрируема на интервале $[a, b]$ , и пусть $f$ допускает первообразную $F$ на $(a, b)$ такую, что $F$ непрерывна на $[a, b]$ . Начните с количества $F (б) - F (а)$ . Пусть существуют числа $x 0, ..., x n$ такие, что

a=x_{0}<x_{1}<x_{2}<\cdots <x_{n-1}<x_{n}=b.

Следует, что

F(b)-F(a)=F(x_{n})-F(x_{0}).

Теперь мы добавляем каждый $F (x i)$ вместе с его аддитивным обратным, чтобы полученная величина была равна:

{\begin{aligned}F(b)-F(a)&=F(x_{n})+[-F(x_{n-1})+F(x_{n-1})]+\cdots +[-F(x_{1})+F(x_{1})]-F(x_{0})\\&=[F(x_{n})-F(x_{n-1})]+[F(x_{n-1})-F(x_{n-2})]+\cdots +[F(x_{2})-F(x_{1})]+[F(x_{1})-F(x_{0})].\end{aligned}}

Вышеуказанную величину можно записать в виде следующей суммы:

F(b)-F(a)=\sum _{i=1}^{n}[F(x_{i})-F(x_{i-1})].

( 1' )

Функция $F$ дифференцируема на отрезке $(a, b)$ и непрерывна на отрезке $[a, b]$ ; следовательно, он также дифференцируем на каждом интервале $(x i -1, x i)$ и непрерывен на каждом интервале $[x i -1, x i]$ . Согласно теореме о среднем значении (см. выше), для каждого $i$ существует $c_{i}$ in $(x i -1, x i)$ такой, что

F(x_{i})-F(x_{i-1})=F'(c_{i})(x_{i}-x_{i-1}).

Подставив сказанное выше в ( 1' ), получим

F(b)-F(a)=\sum _{i=1}^{n}[F'(c_{i})(x_{i}-x_{i-1})].

Это предположение подразумевает $F'(c_{i})=f(c_{i}).$ Также, $x_{i}-x_{i-1}$ может быть выражено как $\Delta x$ раздела $i$ .

F(b)-F(a)=\sum _{i=1}^{n}[f(c_{i})(\Delta x_{i})].

( 2' )

Сходящаяся последовательность сумм Римана. Число в левом верхнем углу — это общая площадь синих прямоугольников. Они сходятся к определенному интегралу функции.

Мы описываем площадь прямоугольника, умножив ширину на высоту, и складываем площади. Каждый прямоугольник в силу теоремы о среднем значении описывает аппроксимацию участка кривой, над которым он нарисован. Также $\Delta x_{i}$ не обязательно должно быть одинаковым для всех значений $i$ или, другими словами, ширина прямоугольников может различаться. Нам нужно аппроксимировать кривую $n$ прямоугольниками. Теперь, когда размер разделов становится меньше, а $n$ увеличивается, что приводит к увеличению количества разделов, покрывающих пространство, мы приближаемся все ближе и ближе к фактической площади кривой.

Взяв предел выражения при стремлении нормы разбиения к нулю, мы приходим к интегралу Римана . Мы знаем, что этот предел существует, поскольку $f$ предполагалось, что интегрируема. То есть мы принимаем предел, когда размер самого большого из разделов приближается к нулю, так что все остальные разделы становятся меньше, а количество разделов приближается к бесконечности.

Итак, мы берем предел по обе стороны от ( 2' ). Это дает нам

\lim _{\|\Delta x_{i}\|\to 0}F(b)-F(a)=\lim _{\|\Delta x_{i}\|\to 0}\sum _{i=1}^{n}[f(c_{i})(\Delta x_{i})].

Ни $F (b)$ , ни $F (a)$ не зависят от $\|\Delta x_{i}\|$ , поэтому предел слева остается $F (b) - F (a)$ .

F(b)-F(a)=\lim _{\|\Delta x_{i}\|\to 0}\sum _{i=1}^{n}[f(c_{i})(\Delta x_{i})].

Выражение в правой части уравнения определяет интеграл по $f$ от $a$ до $b$ . Таким образом, мы получаем

F(b)-F(a)=\int _{a}^{b}f(x)\,dx,

что завершает доказательство.

Связь между частями [ править ]

Как обсуждалось выше, из первой части следует несколько более слабая версия второй части.

Точно так же кажется, что первая часть теоремы непосредственно вытекает из второй. То есть предположим, что $G$ является первообразной $f$ . Тогда по второй теореме ${\textstyle G(x)-G(a)=\int _{a}^{x}f(t)\,dt}$ . Теперь предположим ${\textstyle F(x)=\int _{a}^{x}f(t)\,dt=G(x)-G(a)}$ . Тогда $F$ имеет ту же производную, что и $G$ , и, следовательно, $F' = f$ . Однако этот аргумент работает только в том случае, если мы уже знаем, что $f$ имеет первообразную, а единственный способ узнать, что все непрерывные функции имеют первообразные, — это использовать первую часть Основной теоремы. ^[9] Например, если $f (x) = e - х 2$ , то $f$ имеет первообразную, а именно

G(x)=\int _{0}^{x}f(t)\,dt

и более простого выражения для этой функции не существует. Поэтому важно не интерпретировать вторую часть теоремы как определение интеграла. Действительно, существует множество функций, которые интегрируемы, но не имеют элементарных первообразных , а разрывные функции могут быть интегрируемы, но вообще не иметь первообразных. И наоборот, многие функции, имеющие первообразные, не интегрируемы по Риману (см. функцию Вольтерра ).

Примеры [ править ]

Вычисление конкретного интеграла [ править ]

Предположим, что необходимо вычислить следующее:

\int _{2}^{5}x^{2}\,dx.

Здесь, $f(x)=x^{2}$ и мы можем использовать ${\textstyle F(x)={\frac {1}{3}}x^{3}}$ как первообразная. Поэтому:

\int _{2}^{5}x^{2}\,dx=F(5)-F(2)={\frac {5^{3}}{3}}-{\frac {2^{3}}{3}}={\frac {125}{3}}-{\frac {8}{3}}={\frac {117}{3}}=39.

Использование первой части [ править ]

Предполагать

{\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt

предстоит рассчитать. Используя первую часть теоремы с

f(t)=t^{3}

дает

{\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt=f(x)=x^{3}.

Это также можно проверить с помощью второй части теоремы. Конкретно, ${\textstyle F(t)={\frac {1}{4}}t^{4}}$ является первообразной от $f(t)$ , так

{\frac {d}{dx}}\int _{0}^{x}t^{3}\,dt={\frac {d}{dx}}F(x)-{\frac {d}{dx}}F(0)={\frac {d}{dx}}{\frac {x^{4}}{4}}=x^{3}.

Интеграл, в недостаточно следствие котором

Предполагать

f(x)={\begin{cases}\sin \left({\frac {1}{x}}\right)-{\frac {1}{x}}\cos \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0\\\end{cases}}

Затем

f(x)

не является непрерывным в нуле. Более того, дело не только в том, как

f

определяется в нуле, поскольку предел как

x\to 0

из

f(x)

не существует. Следовательно, следствие не может быть использовано для вычисления

\int _{0}^{1}f(x)\,dx.

Но рассмотрим функцию

F(x)={\begin{cases}x\sin \left({\frac {1}{x}}\right)&x\neq 0\\0&x=0.\\\end{cases}}

Заметить, что

F(x)

постоянно включен

[0,1]

(в том числе и в нуле по теореме о сжатии ), и

F(x)

дифференцируема по

(0,1)

с

F'(x)=f(x).

Следовательно, применима часть вторая теоремы, и

\int _{0}^{1}f(x)\,dx=F(1)-F(0)=\sin(1).

Теоретический пример [ править ]

Теорему можно использовать для доказательства того, что

\int _{a}^{b}f(x)dx=\int _{a}^{c}f(x)dx+\int _{c}^{b}f(x)dx.

С,

{\begin{aligned}\int _{a}^{b}f(x)dx&=F(b)-F(a),\\\int _{a}^{c}f(x)dx&=F(c)-F(a),{\text{ and }}\\\int _{c}^{b}f(x)dx&=F(b)-F(c),\end{aligned}}

результат следует из того,

F(b)-F(a)=F(c)-F(a)+F(b)-F(c).

Обобщения [ править ]

Функция $f$ не обязательно должна быть непрерывной на всем интервале. Тогда часть I теоремы гласит: если $f$ — любая интегрируемая по Лебегу функция на $[a, b]$ и $x0 f$ — число из $[a, b]$ такое, что $непрерывна$ в точке $, x0$ то

F(x)=\int _{a}^{x}f(t)\,dt

дифференцируемо для $x = x 0$ с $F'(x 0) = f (x 0)$ . Мы можем еще больше ослабить условия на $f$ и предположить, что она просто локально интегрируема. В этом случае можно заключить, что функция $F$ дифференцируема почти всюду и $F'(x) = f (x)$ почти всюду. На вещественной прямой это утверждение эквивалентно теореме дифференцирования Лебега . Эти результаты остаются верными для интеграла Хенстока – Курцвейла , который допускает более широкий класс интегрируемых функций. ^[10]

В более высоких измерениях теорема дифференцирования Лебега обобщает Фундаментальную теорему исчисления, утверждая, что почти для каждого $x$ среднее значение функции $f$ по шару радиуса $r$ с центром в $x$ стремится к $f (x)$ , когда $r$ стремится к 0.

Часть II теоремы верна для любой интегрируемой по Лебегу функции $f$ , которая имеет первообразную $F$ (однако не все интегрируемые функции имеют первообразную). Другими словами, если действительная функция $F$ на $[a, b]$ допускает производную $f (x)$ в каждой точке $x$ из $[a, b]$ и если эта производная $f$ интегрируема по Лебегу на $[a, b]$ , то ^[11]

F(b)-F(a)=\int _{a}^{b}f(t)\,dt.

Этот результат может оказаться неверным для непрерывных функций $F$ , которые допускают производную $f (x)$ почти в каждой точке $x$ , как показывает пример функции Кантора . Однако, если $F$ , абсолютно непрерывен он допускает производную $F ' (x)$ почти в каждой точке $x$ , и, более того, $F '$ интегрируем, причем $F (b) - F (a)$ равен интегралу от $F '$ на $[a, б]$ . И наоборот, если $f$ — любая интегрируемая функция, то $F$ , заданная в первой формуле, будет абсолютно непрерывна, причем $F ' = f$ почти всюду.

Условия этой теоремы можно снова ослабить, если рассматривать рассматриваемые интегралы как интегралы Хенстока – Курцвейла . В частности, если непрерывная функция $F (x)$ допускает производную $f (x)$ во всех точках, кроме счетного числа, то $f (x)$ интегрируема по Хенстоку – Курцвейлу и $F (b) - F (a)$ равна интегралу от $f$ на $[a, b]$ . интегрируемость $f .$ Разница здесь в том, что не нужно предполагать ^[12]

Вариант теоремы Тейлора , выражающий член ошибки в виде интеграла, можно рассматривать как обобщение фундаментальной теоремы.

Существует версия теоремы для комплексных функций: предположим, что $U$ — открытое множество в $C$ и $f : U \to C$ — функция, голоморфную первообразную $F$ на $U.$ имеющая Тогда для каждой кривой $γ: [a, b] \to U$ можно интеграл кривой вычислить как

\int _{\gamma }f(z)\,dz=F(\gamma (b))-F(\gamma (a)).

Фундаментальную теорему можно обобщить на кривые и поверхностные интегралы в более высоких измерениях и на многообразиях . Одним из таких обобщений, предлагаемых исчислением движущихся поверхностей, является эволюция интегралов во времени . Наиболее известными расширениями фундаментальной теоремы исчисления в высших измерениях являются теорема о дивергенции и теорема о градиенте .

Одним из наиболее мощных обобщений в этом направлении является теорема Стокса (иногда известная как фундаментальная теорема исчисления многих переменных): ^[13] Пусть $M$ — ориентированное кусочно- гладкое многообразие размерности n $и$ пусть $\omega$ — гладкая с компактным носителем $(n - 1)$ -форма на $M$ . Если $\partialM обозначает$ границу с учетом M $его$ индуцированной ориентации , то

\int _{M}d\omega =\int _{\partial M}\omega .

Здесь $d$ — внешняя производная , которая определяется только с использованием структуры многообразия.

Теорема часто используется в ситуациях, когда $M$ является вложенным ориентированным подмногообразием некоторого большего многообразия (например, $R к$ ), на котором форма $\omega$ определено.

Основная теорема исчисления позволяет представить определенный интеграл как обыкновенное дифференциальное уравнение первого порядка.

\int _{a}^{b}f(x)\,dx

можно представить как

{\frac {dy}{dx}}=f(x),\;\;y(a)=0

с

y(b)

как значение интеграла.

См. также [ править ]

Примечания [ править ]

Ссылки [ править ]

^ Вайсштейн, Эрик В. «Первая фундаментальная теорема исчисления» . mathworld.wolfram.com . Проверено 15 апреля 2024 г.
^ Малет, Антони (1993). «Джеймс Грегори о касательных и правиле Тейлора для разложения рядов». Архив истории точных наук . 46 (2). Спрингер-Верлаг : 97–137. дои : 10.1007/BF00375656 . S2CID 120101519 . С другой стороны, мысль Грегори принадлежит концептуальной системе, строго геометрической по своему характеру. (стр. 137)
^ См., например, Марлоу Андерсон, Виктор Дж. Кац, Робин Дж. Уилсон, Шерлок Холмс в Вавилоне и другие рассказы математической истории , Математическая ассоциация Америки, 2004, с. 114 .
^ Грегори, Джеймс (1668). Универсальная часть геометрии . Музей Галилея : Патавии: типы, унаследованные Полем Фрамботти.
^ Чайлд, Джеймс Марк; Барроу, Исаак (1916). Геометрические лекции Исаака Барроу . Чикаго: Издательская компания Open Court .
^ Апостол 1967 , §5.1
^ Апостол 1967 , §5.3
^ Лейтольд, Л. (1996), Исчисление одной переменной (6-е изд.), Нью-Йорк: HarperCollins College Publishers, стр. 380 .
^ Спивак, Майкл (1980), Исчисление (2-е изд.), Хьюстон, Техас: Publish or Perish Inc.
^ Бартл (2001) , Thm. 4.11.
^ Рудин 1987 , th. 7.21
^ Бартл (2001) , Thm. 4.7.
^ Спивак, М. (1965). Исчисление на многообразиях . Нью-Йорк: WA Бенджамин. стр. 124–125. ISBN 978-0-8053-9021-6 .

Библиография [ править ]

Апостол, Том М. (1967), Исчисление, Том. 1: Исчисление с одной переменной и введение в линейную алгебру (2-е изд.), Нью-Йорк: John Wiley & Sons , ISBN 978-0-471-00005-1 .
Бартл, Роберт (2001), Современная теория интеграции , AMS, ISBN 0-8218-0845-1 .
Лейтольд, Л. (1996), Исчисление одной переменной (6-е изд.), Нью-Йорк: издательство HarperCollins College Publishers .
Рудин, Уолтер (1987), Реальный и комплексный анализ (третье изд.), Нью-Йорк: McGraw-Hill Book Co., ISBN 0-07-054234-1

Дальнейшее чтение [ править ]

Курант, Ричард; Джон, Фриц (1965), «Введение в исчисление и анализ» , Springer .
Ларсон, Рон; Эдвардс, Брюс Х.; Хейд, Дэвид Э. (2002), Исчисление одной переменной (7-е изд.), Бостон: Houghton Mifflin Company, ISBN 978-0-618-14916-2 .
Малет, А. , Исследования Джеймса Грегори (1638-1675) (докторская диссертация, Принстон, 1989).
Эрнандес Родригес, ОА; Лопес Фернандес, JM. « Обучение фундаментальной теореме исчисления: историческое размышление », Loci: Convergence ( MAA ), январь 2012 г.
Стюарт, Дж. (2003), «Фундаментальная теорема исчисления», Исчисление: ранние трансцендентальные теории , Белмонт, Калифорния: Томсон/Брукс/Коул .
Тернбулл, HW, изд. (1939), Мемориальный том к трехсотлетию Джеймса Грегори , Лондон {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) .

Внешние ссылки [ править ]

[1] Вайсштейн, Эрик В. «Первая фундаментальная теорема исчисления» . mathworld.wolfram.com . Проверено 15 апреля 2024 г.

[GregoryGeometry-2] Малет, Антони (1993). «Джеймс Грегори о касательных и правиле Тейлора для разложения рядов». Архив истории точных наук . 46 (2). Спрингер-Верлаг : 97–137. дои : 10.1007/BF00375656 . S2CID 120101519 . С другой стороны, мысль Грегори принадлежит концептуальной системе, строго геометрической по своему характеру. (стр. 137)

[3] См., например, Марлоу Андерсон, Виктор Дж. Кац, Робин Дж. Уилсон, Шерлок Холмс в Вавилоне и другие рассказы математической истории , Математическая ассоциация Америки, 2004, с. 114 .

[geometriae-4] Грегори, Джеймс (1668). Универсальная часть геометрии . Музей Галилея : Патавии: типы, унаследованные Полем Фрамботти.

[BarrowGeometricLectures-5] Чайлд, Джеймс Марк; Барроу, Исаак (1916). Геометрические лекции Исаака Барроу . Чикаго: Издательская компания Open Court .

[6] Апостол 1967 , §5.1

[7] Апостол 1967 , §5.3

[8] Лейтольд, Л. (1996), Исчисление одной переменной (6-е изд.), Нью-Йорк: HarperCollins College Publishers, стр. 380 .

[Spivak-9] Спивак, Майкл (1980), Исчисление (2-е изд.), Хьюстон, Техас: Publish or Perish Inc.

[FOOTNOTEBartle2001Thm._4.11-10] Бартл (2001) , Thm. 4.11.

[11] Рудин 1987 , th. 7.21

[FOOTNOTEBartle2001Thm._4.7-12] Бартл (2001) , Thm. 4.7.

[13] Спивак, М. (1965). Исчисление на многообразиях . Нью-Йорк: WA Бенджамин. стр. 124–125. ISBN 978-0-8053-9021-6 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

v т Это Исчисление
Precalculus	Binomial theorem Concave function Continuous function Factorial Finite difference Free variables and bound variables Graph of a function Linear function Radian Rolle's theorem Secant Slope Tangent
Limits	Indeterminate form Limit of a function One-sided limit Limit of a sequence Order of approximation (ε, δ)-definition of limit
Differential calculus	Derivative Second derivative Partial derivative Differential Differential operator Mean value theorem Notation Leibniz's notation Newton's notation Rules of differentiation linearity Power Sum Chain L'Hôpital's Product General Leibniz's rule Quotient Other techniques Implicit differentiation Inverse functions and differentiation Logarithmic derivative Related rates Stationary points First derivative test Second derivative test Extreme value theorem Maximum and minimum Further applications Newton's method Taylor's theorem Differential equation Ordinary differential equation Partial differential equation Stochastic differential equation
Integral calculus	Antiderivative Arc length Riemann integral Basic properties Constant of integration Fundamental theorem of calculus Differentiating under the integral sign Integration by parts Integration by substitution trigonometric Euler Tangent half-angle substitution Partial fractions in integration Quadratic integral Trapezoidal rule Volumes Washer method Shell method Integral equation Integro-differential equation
Vector calculus	Derivatives Curl Directional derivative Divergence Gradient Laplacian Basic theorems Line integrals Green's Stokes' Gauss'
Multivariable calculus	Divergence theorem Geometric Hessian matrix Jacobian matrix and determinant Lagrange multiplier Line integral Matrix Multiple integral Partial derivative Surface integral Volume integral Advanced topics Differential forms Exterior derivative Generalized Stokes' theorem Tensor calculus
Sequences and series	Arithmetico-geometric sequence Types of series Alternating Binomial Fourier Geometric Harmonic Infinite Power Maclaurin Taylor Telescoping Tests of convergence Abel's Alternating series Cauchy condensation Direct comparison Dirichlet's Integral Limit comparison Ratio Root Term
Special functions and numbers	Bernoulli numbers e (mathematical constant) Exponential function Natural logarithm Stirling's approximation
History of calculus	Adequality Brook Taylor Colin Maclaurin Generality of algebra Gottfried Wilhelm Leibniz Infinitesimal Infinitesimal calculus Isaac Newton Fluxion Law of Continuity Leonhard Euler Method of Fluxions The Method of Mechanical Theorems
Lists	Differentiation rules List of integrals of exponential functions List of integrals of hyperbolic functions List of integrals of inverse hyperbolic functions List of integrals of inverse trigonometric functions List of integrals of irrational functions List of integrals of logarithmic functions List of integrals of rational functions List of integrals of trigonometric functions Secant Secant cubed List of limits Lists of integrals
Miscellaneous topics	Complex calculus Contour integral Differential geometry Manifold Curvature of curves of surfaces Tensor Euler–Maclaurin formula Gabriel's horn Integration Bee Proof that 22/7 exceeds π Regiomontanus' angle maximization problem Steinmetz solid

v т Это Основные темы математического анализа
Calculus: Integration Differentiation Differential equations ordinary partial stochastic Fundamental theorem of calculus Calculus of variations Vector calculus Tensor calculus Matrix calculus Lists of integrals Table of derivatives
Real analysis Complex analysis Hypercomplex analysis (quaternionic analysis) Functional analysis Fourier analysis Least-squares spectral analysis Harmonic analysis P-adic analysis (P-adic numbers) Measure theory Representation theory Functions Continuous function Special functions Limit Series Infinity
Mathematics portal